数学人教A版(2019)选择性必修第一册1.3空间向量的坐标及其坐标运算(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.3空间向量的坐标及其坐标运算(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 582.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
选修第一册 第1章→空间向量的坐标
新课导入
借鉴平面向量的经验,平面向量是如何解决的?
空间向量问题也能如此吗?
向量的基底化,为向量的运算带来极大的方便,但向量带基
底运算有时依然很麻烦,有更高级的方法吗?
向量坐标化
选修第一册 第1章→空间向量的坐标
新课导入
§3 空间向量的坐标及坐标运算
选修第一册 第1章→空间向量的坐标
新课导入
§3.1 空间向量的坐标
选修第一册 第1章→空间向量的坐标
新课导入
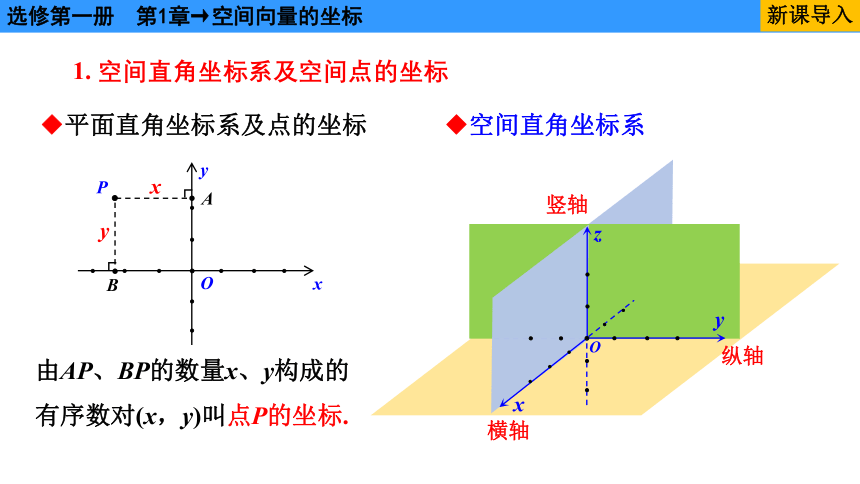
1. 空间直角坐标系及空间点的坐标
◆平面直角坐标系及点的坐标
O
x
y
◆空间直角坐标系
P
x
y
由AP、BP的数量x、y构成的
有序数对(x,y)叫点P的坐标.
y
纵轴
竖轴
横轴
z
x
O
A
∟
B
∟
y
z
x
O
选修第一册 第1章→空间向量的坐标
新课导入
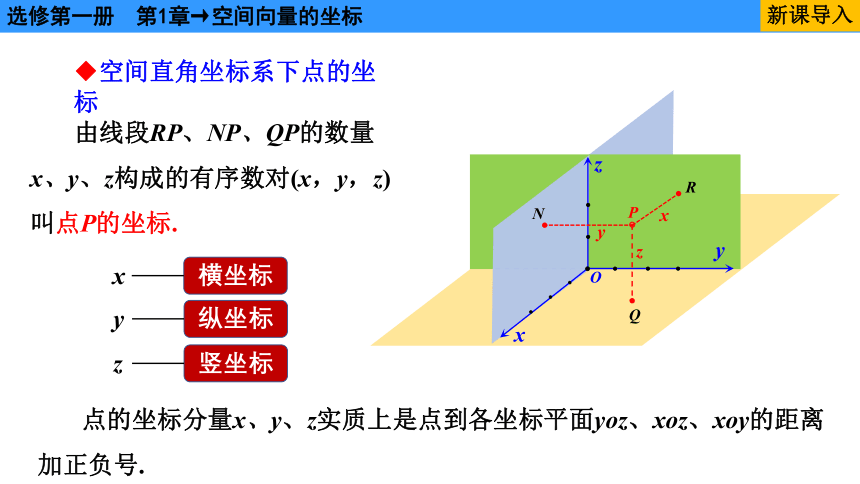
◆空间直角坐标系下点的坐标
x
P
R
Q
y
z
由线段RP、NP、QP的数量
x、y、z构成的有序数对(x,y,z)
叫点P的坐标.
x
横坐标
y
纵坐标
z
竖坐标
点的坐标分量x、y、z实质上是点到各坐标平面yoz、xoz、xoy的距离
加正负号.
N
y
z
x
选修第一册 第1章→空间向量的坐标及坐标运算
新课导入
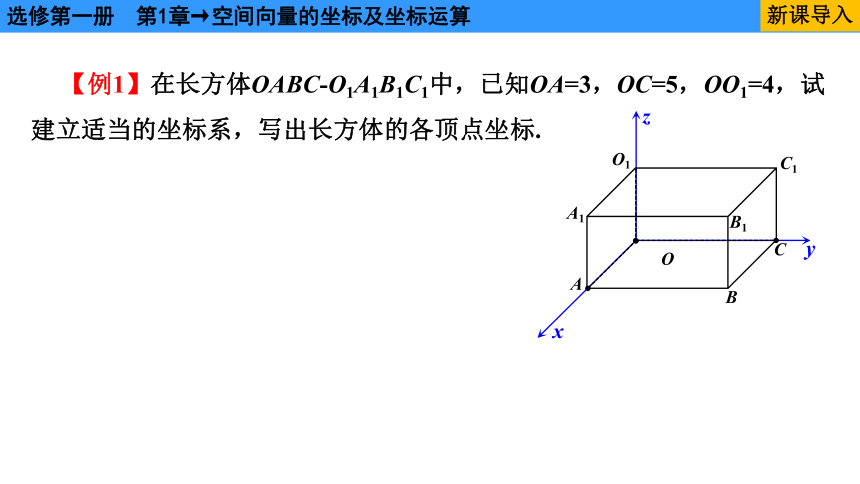
【例1】在长方体OABC-O1A1B1C1中,已知OA=3,OC=5,OO1=4,试建立适当的坐标系,写出长方体的各顶点坐标.
A
B
O
C
O1
A1
B1
C1
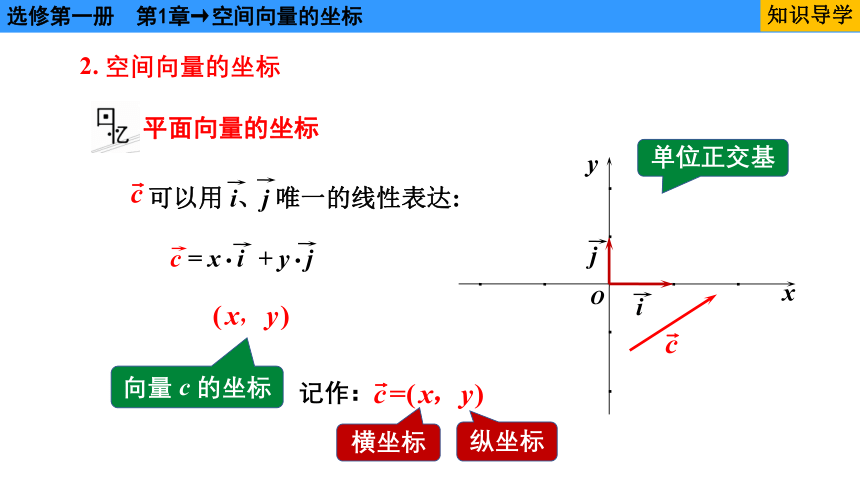
向量 c 的坐标
O
x
y
单位正交基
可以用 i、j 唯一的线性表达:
i
c = x i +y j
横坐标
纵坐标
记作:
平面向量的坐标
j
选修第一册 第1章→空间向量的坐标
知识导学
2. 空间向量的坐标
O
x
z
y
向量 c 的坐标
单位正交基
j
横坐标
纵坐标
记作:
k
i
可以用 唯一的线性表达:
竖坐标
选修第一册 第1章→空间向量的坐标
知识导学
空间向量的坐标的定义
在空间直角坐标系中,选 x轴、y轴和z轴的正向上的单位向量 为基底,空间任一向量 c 用基底表达:
表达式的系数构成的有序数对 (x,y,z),叫做向量 c 的坐标.
x
横坐标
y
纵坐标
z
竖坐标
选修第一册 第1章→空间向量的坐标
知识导学
【注意】:
(1)空间向量的坐标与点的坐标,虽然长得一样,但本质不同;
▲平移点,点的坐标会改变,但平移向量不改变向量的坐标;
a
▲点的坐标,刻画点的位置,向量的坐标刻画向量的大小与方向.
P
O
y
z
x
a
P
选修第一册 第1章→空间向量的坐标
知识导学
【注意】:
(2)空间向量的坐标与点的坐标的关系:
N
以原点为起点的向量的坐标,就是该向量的终点坐标.
M(x,y,z)
①以原点为起点的向量
(x,y)
②若P(x1,y1,z1),Q(x2,y2,z2) 则:
选修第一册 第1章→空间向量的坐标
知识导学
O
x
z
y
●
●
●
●
●
●
●
●
●
【例2】根据图中数据,写出A,B,C,D,M,N各点的坐标(其中DC//x轴,N为AC的中点),并求写出 的坐标.
z
O
y
2
4
-2
-4
2
4
A
2
4
x
B
C
D
M
N
选修第一册 第1章→空间向量的坐标
知识导学
完成教材P18练习T2,T3,T4
选修第一册 第1章→空间向量的坐标
知识导学
【课堂小结】
空间直角坐标系
空间向量的坐标
点的坐标与向量的坐标关系
空间向量坐标的求法
空间点的坐标
选修第一册 第1章→空间向量的坐标及坐标运算
知识导学
本部分内容讲解结束
按ESC键退出全屏播放
选修第一册 第1章→空间向量的坐标
新课导入
借鉴平面向量的经验,平面向量是如何解决的?
空间向量问题也能如此吗?
向量的基底化,为向量的运算带来极大的方便,但向量带基
底运算有时依然很麻烦,有更高级的方法吗?
向量坐标化
选修第一册 第1章→空间向量的坐标
新课导入
§3 空间向量的坐标及坐标运算
选修第一册 第1章→空间向量的坐标
新课导入
§3.1 空间向量的坐标
选修第一册 第1章→空间向量的坐标
新课导入
1. 空间直角坐标系及空间点的坐标
◆平面直角坐标系及点的坐标
O
x
y
◆空间直角坐标系
P
x
y
由AP、BP的数量x、y构成的
有序数对(x,y)叫点P的坐标.
y
纵轴
竖轴
横轴
z
x
O
A
∟
B
∟
y
z
x
O
选修第一册 第1章→空间向量的坐标
新课导入
◆空间直角坐标系下点的坐标
x
P
R
Q
y
z
由线段RP、NP、QP的数量
x、y、z构成的有序数对(x,y,z)
叫点P的坐标.
x
横坐标
y
纵坐标
z
竖坐标
点的坐标分量x、y、z实质上是点到各坐标平面yoz、xoz、xoy的距离
加正负号.
N
y
z
x
选修第一册 第1章→空间向量的坐标及坐标运算
新课导入
【例1】在长方体OABC-O1A1B1C1中,已知OA=3,OC=5,OO1=4,试建立适当的坐标系,写出长方体的各顶点坐标.
A
B
O
C
O1
A1
B1
C1
向量 c 的坐标
O
x
y
单位正交基
可以用 i、j 唯一的线性表达:
i
c = x i +y j
横坐标
纵坐标
记作:
平面向量的坐标
j
选修第一册 第1章→空间向量的坐标
知识导学
2. 空间向量的坐标
O
x
z
y
向量 c 的坐标
单位正交基
j
横坐标
纵坐标
记作:
k
i
可以用 唯一的线性表达:
竖坐标
选修第一册 第1章→空间向量的坐标
知识导学
空间向量的坐标的定义
在空间直角坐标系中,选 x轴、y轴和z轴的正向上的单位向量 为基底,空间任一向量 c 用基底表达:
表达式的系数构成的有序数对 (x,y,z),叫做向量 c 的坐标.
x
横坐标
y
纵坐标
z
竖坐标
选修第一册 第1章→空间向量的坐标
知识导学
【注意】:
(1)空间向量的坐标与点的坐标,虽然长得一样,但本质不同;
▲平移点,点的坐标会改变,但平移向量不改变向量的坐标;
a
▲点的坐标,刻画点的位置,向量的坐标刻画向量的大小与方向.
P
O
y
z
x
a
P
选修第一册 第1章→空间向量的坐标
知识导学
【注意】:
(2)空间向量的坐标与点的坐标的关系:
N
以原点为起点的向量的坐标,就是该向量的终点坐标.
M(x,y,z)
①以原点为起点的向量
(x,y)
②若P(x1,y1,z1),Q(x2,y2,z2) 则:
选修第一册 第1章→空间向量的坐标
知识导学
O
x
z
y
●
●
●
●
●
●
●
●
●
【例2】根据图中数据,写出A,B,C,D,M,N各点的坐标(其中DC//x轴,N为AC的中点),并求写出 的坐标.
z
O
y
2
4
-2
-4
2
4
A
2
4
x
B
C
D
M
N
选修第一册 第1章→空间向量的坐标
知识导学
完成教材P18练习T2,T3,T4
选修第一册 第1章→空间向量的坐标
知识导学
【课堂小结】
空间直角坐标系
空间向量的坐标
点的坐标与向量的坐标关系
空间向量坐标的求法
空间点的坐标
选修第一册 第1章→空间向量的坐标及坐标运算
知识导学
本部分内容讲解结束
按ESC键退出全屏播放
