相似三角形与位似图形[下学期]
图片预览





文档简介
课件25张PPT。努力现在,成就未来
《中考数学新航标》
第七章第二节
知识点聚焦
回头找感觉
例题讨论
过关训练相似三角形与位似图形知识点聚焦一、相似三角形的识别方法有哪些?
二、相似三角形的特征是什么?
(相似与全等的关系?)
三、什么叫位似?
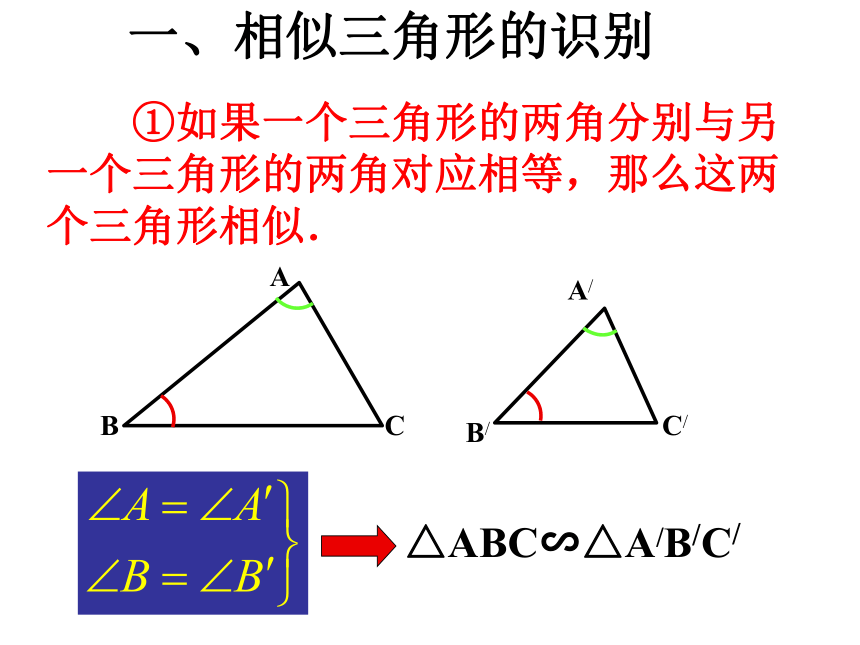
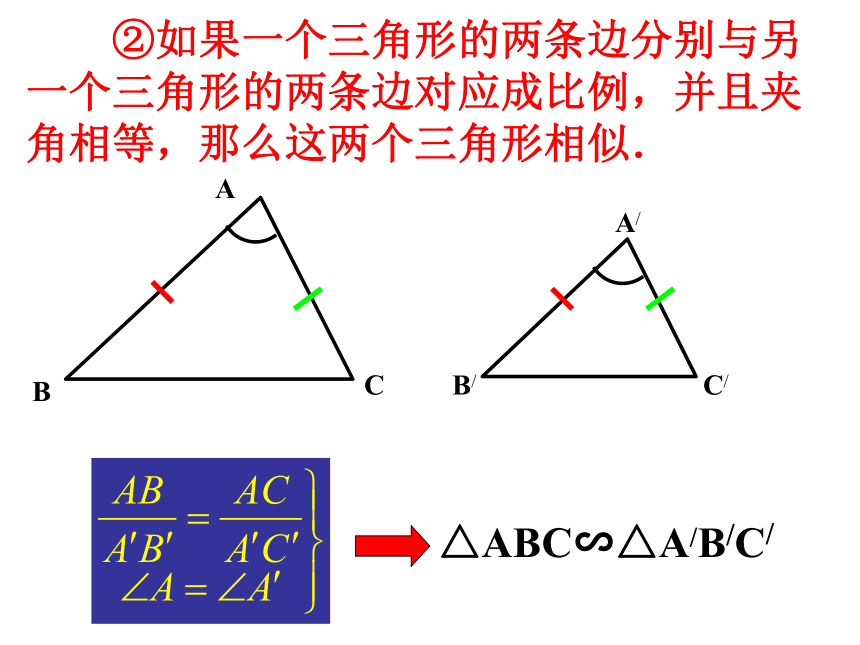
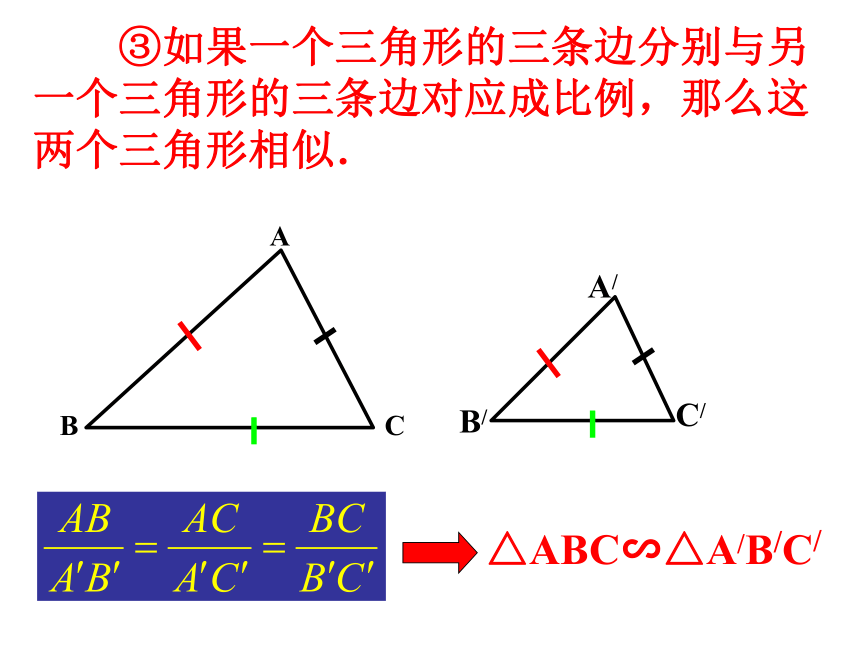
(相似与位似的关系?)一、相似三角形的识别 ①如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.AA/CBC/B/ ②如果一个三角形的两条边分别与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似. ③如果一个三角形的三条边分别与另一个三角形的三条边对应成比例,那么这两个三角形相似.B/A/C/ABC两个相似三角形的①对应边成比例,对应角相等;
②对应高的比、对应中线的比、对应角平分线的比都等于相似比;
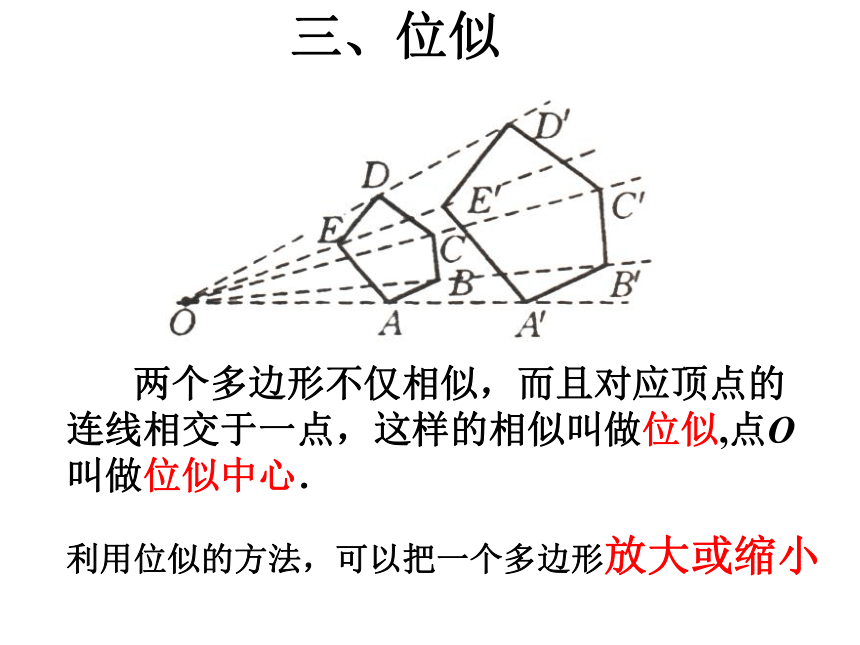
③周长的比等于相似比;面积的比等于相似比的平方.二、相似三角形的特征三、位似 两个多边形不仅相似,而且对应顶点的连线相交于一点,这样的相似叫做位似,点O叫做位似中心.利用位似的方法,可以把一个多边形放大或缩小回头找感觉1、比例尺是1:100000的地图上,量得甲乙两地 的距离为3厘米则两地的实际距离是 千米。
2、如果两个三角形相似,相似比为3:5,则对应高的比是 、周长的比是 、面积的比是 。
3、如图,当 时, △ABC∽ △ADE.
若AB=6、AE=2、AD=3,
则AC= .?433:53:59:255、如图,已知 平行四边形ABCD中,A、E、F共线,B、C、F共线,则与△FCE相似的三角形有 和 。 4、下列命题正确的是 ( )
A.所有的直角三角形都相似
B.所有的等腰三角形都相似
C.所有的等腰直角三角形都相似
D.所有的菱形都相似C△FBA △A DE 6、三角形相似有哪些基本图形?例题讨论例1、如图,D是△ABC的边AC上的一点,过点D画线段DE,使点E在△ABC的边上,并且点D、点E和△ABC的一个顶点组成的小三角形与△ABC相似,问这样的DE有几种画法?例2、如图,已知:AB⊥DB于点B ,CD⊥DB于点D,AB=6,CD=4,BD=14.
问:在DB上是否存在P点,使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似?如果存在,计算出点P的位置;如果不存在,请说明理由。解(1)假设存在这样的点P,使△ABP∽△CDP
设PD=x,则PB=14―x,
∴6:4=(14―x):x则有AB:CD=PB:PD∴x=5.6P(2)假设存在这样的点P,使△ABP∽△PDC,则
则有AB:PD=PB:CD设PD=x,则PB=14―x,
∴6: x =(14―x): 4∴x=2或x=12∴x=2或x=12或x=5.6时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似46x14―xDBCAp例3方法小结把相似三角形的一些基本图形归类,熟记一些基本的方法,可以帮助我们解决问题。以相似三角形为背景的综合题,要充分运用方程、分类讨论、转化、函数以及数形结合的思想来研究解决。(1)~(4)题,见《航标》第160页2、3、4、10。过关训练②探究:在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。Q作业1、157页:例2(2)
2、162页:11、12感谢各位老师的光临指导!再见(1)、 在?ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB边向B点以2cm/秒的速度移动,点Q从点B开始沿BC向点C以4cm/秒的速度移动,如果P、Q分别从A、B同时出发,经几秒钟?BPQ与?BAC相似?分析:由于?PBQ与?ABC有公共角∠B;所以若?PBQ与?ABC相似,则有两种可能一种情况为 ,即PQ∥AC;另一种情况为 (2)、如图所示,Rt△ABC中,∠C=90°,AC=4,BC=3,DE∥BC,设AE=x,四边形BDEC的面积为y,则y可表示成x的函数,其图像的形状是 ( )
A.开口向上的抛物线的一部分
B.开口向下的抛物线的一部分
C.线段(不包括两个端点)
D.双曲线的一部分 B
《中考数学新航标》
第七章第二节
知识点聚焦
回头找感觉
例题讨论
过关训练相似三角形与位似图形知识点聚焦一、相似三角形的识别方法有哪些?
二、相似三角形的特征是什么?
(相似与全等的关系?)
三、什么叫位似?
(相似与位似的关系?)一、相似三角形的识别 ①如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.AA/CBC/B/ ②如果一个三角形的两条边分别与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似. ③如果一个三角形的三条边分别与另一个三角形的三条边对应成比例,那么这两个三角形相似.B/A/C/ABC两个相似三角形的①对应边成比例,对应角相等;
②对应高的比、对应中线的比、对应角平分线的比都等于相似比;
③周长的比等于相似比;面积的比等于相似比的平方.二、相似三角形的特征三、位似 两个多边形不仅相似,而且对应顶点的连线相交于一点,这样的相似叫做位似,点O叫做位似中心.利用位似的方法,可以把一个多边形放大或缩小回头找感觉1、比例尺是1:100000的地图上,量得甲乙两地 的距离为3厘米则两地的实际距离是 千米。
2、如果两个三角形相似,相似比为3:5,则对应高的比是 、周长的比是 、面积的比是 。
3、如图,当 时, △ABC∽ △ADE.
若AB=6、AE=2、AD=3,
则AC= .?433:53:59:255、如图,已知 平行四边形ABCD中,A、E、F共线,B、C、F共线,则与△FCE相似的三角形有 和 。 4、下列命题正确的是 ( )
A.所有的直角三角形都相似
B.所有的等腰三角形都相似
C.所有的等腰直角三角形都相似
D.所有的菱形都相似C△FBA △A DE 6、三角形相似有哪些基本图形?例题讨论例1、如图,D是△ABC的边AC上的一点,过点D画线段DE,使点E在△ABC的边上,并且点D、点E和△ABC的一个顶点组成的小三角形与△ABC相似,问这样的DE有几种画法?例2、如图,已知:AB⊥DB于点B ,CD⊥DB于点D,AB=6,CD=4,BD=14.
问:在DB上是否存在P点,使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似?如果存在,计算出点P的位置;如果不存在,请说明理由。解(1)假设存在这样的点P,使△ABP∽△CDP
设PD=x,则PB=14―x,
∴6:4=(14―x):x则有AB:CD=PB:PD∴x=5.6P(2)假设存在这样的点P,使△ABP∽△PDC,则
则有AB:PD=PB:CD设PD=x,则PB=14―x,
∴6: x =(14―x): 4∴x=2或x=12∴x=2或x=12或x=5.6时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似46x14―xDBCAp例3方法小结把相似三角形的一些基本图形归类,熟记一些基本的方法,可以帮助我们解决问题。以相似三角形为背景的综合题,要充分运用方程、分类讨论、转化、函数以及数形结合的思想来研究解决。(1)~(4)题,见《航标》第160页2、3、4、10。过关训练②探究:在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。Q作业1、157页:例2(2)
2、162页:11、12感谢各位老师的光临指导!再见(1)、 在?ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB边向B点以2cm/秒的速度移动,点Q从点B开始沿BC向点C以4cm/秒的速度移动,如果P、Q分别从A、B同时出发,经几秒钟?BPQ与?BAC相似?分析:由于?PBQ与?ABC有公共角∠B;所以若?PBQ与?ABC相似,则有两种可能一种情况为 ,即PQ∥AC;另一种情况为 (2)、如图所示,Rt△ABC中,∠C=90°,AC=4,BC=3,DE∥BC,设AE=x,四边形BDEC的面积为y,则y可表示成x的函数,其图像的形状是 ( )
A.开口向上的抛物线的一部分
B.开口向下的抛物线的一部分
C.线段(不包括两个端点)
D.双曲线的一部分 B
