求解平行线三招[下学期]

课件12张PPT。 求解平行线问题的三招
在学习平行线这节内容时常常会出现这样的情况，有的同学一方面对平行线的性质、判定定理背得头头是道，另一方面题目到手却又毫无头绪，不知如何下手。究其原因，主要是对平行线问题的解题策略领会不够，分析问题思路不畅所至。下面向同学们推荐求解平行线问题的三个妙招．
题中出现平行线这个条件．有什么用？如何思考： 联想平行线的性质。题设实质上就是告诉了我们可得相等的同位角、内错角或互补的同旁内角．此法可简记为”平行找角等或补”。
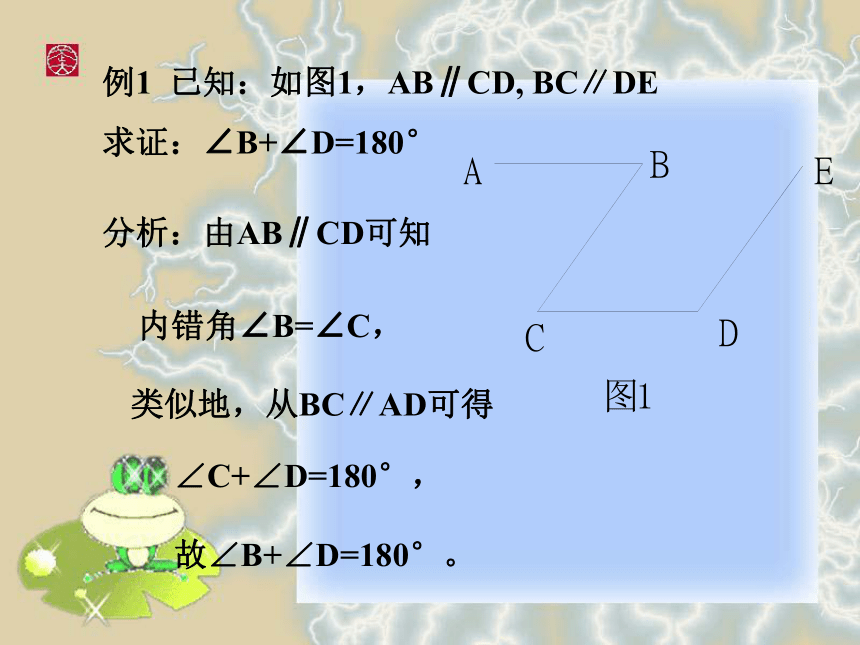
例1 已知：如图1，AB∥CD, BC∥DE
求证：∠B+∠D=180°分析：由AB∥CD可知内错角∠B=∠C，类似地，从BC∥AD可得∠C+∠D=180°，故∠B+∠D=180°。 ??例2??????? 已知， 如图2，DE∥BC，CD是∠ACB的平分线，∠B=70°，∠ACB=50°，
求∠EDC与∠BDC的度数。 分析：从条件联想。
由DE∥BC可得到很多相等和互补的角，到底选用哪些角呢？这是此题和上题的不同之处，也是初学几何证明或计算时感到为难的地方。一般地说，应选用与已知条件和求解结果有关系的角。本题中，选用∠1=∠2，∠3+∠2+∠B=180°这两个关系较好。由CD平分∠ACB知∠1=∠ACB=×50°=25°，由∠B=70°知∠3+∠2=180°－70°=110°，故∠BDC=∠3=110°－∠2=85°。
题中出现的角相等或互补有什么用？ 结合平行线的判定方法，有可能推出两线平行。 同样地，在判定两线平行时，应从同位角相等、内错角相等或同旁内角互补等方面去挖掘条件。 这一过程可记为“角的等补推平行”。例3 已知：如图4，∠1+∠2=180°，求证：∠3=∠4
分析：∠1、∠2和∠3、∠4在位置上没有直接联系，更无数量关系。∠1、∠2互补有何用？ 可以推出两线平行吗？但∠1、∠2不是同旁内角，是否可以转换？从图形中不难发现：∠1=∠5，∠2=∠6。故∠5+∠6=∠180°。由此可得AB∥CD。所以∠3=∠4立即可得。 大家知道，平行线的性质和判定都是建立在“三线八角”这样一个完整图形之上的，因此，一旦题中的图形缺少平行线或第三条直线（通常称为截线），应设法添补直线，以便利用平行线的性质定理或判定定理。 ? ????例4? 如图，已知AB∥DE。
求证：∠BCD=∠B+∠D。
F1分析一 从条件联想联想（1） 条件AB∥DE有何用？按平行线的性质，可得到相等的同位角、内错角及同旁同角。为此，延长BC交DE与F，则∠B=∠1。又∠BCD=∠D+∠1（一外角等于不 相邻的两内角之和），从而∠BCD=∠B+∠D。 类似地，延长DC交AB也可证得此题。联想（2）F12BC、CD作为AB、DE的截线是短了些，为此过C作CF∥AB，由AB∥DE知CF∥DE，从而∠1=∠B，∠2=∠D，故∠BCD=∠1+∠2=∠B+∠D。分析二 由结论分析。1 本题求证结论是∠BCD=∠C+∠D， 从其结构看很象“三角形的一个外角等于不相邻的两个内角之和”， 但图中没有三角形。故延长BC交DE于F（或延长DC交AB）， 此时∠BCD=∠1+∠D=∠B+∠D。F注：分析二和分析一（1）中所添辅助线完全一样，但其思维过程却不尽相同。分析一（1）是从找一条完整的截线为出发点延长BC，分析二却是从构造三角形使∠BCD为一外角作为出发点而延长BC。