第一章集合与常用逻辑 1.4.2充要条件 课件(共21张PPT)
文档属性
| 名称 | 第一章集合与常用逻辑 1.4.2充要条件 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-08 09:58:28 | ||
图片预览








文档简介
(共21张PPT)
第一章 集合与常用逻辑
1.4.2充要条件
教学目标
1.结合具体实例,理解充分条件、必要条件、充要条件的意义.
(重点、难点)
2.会求(判断)某些问题成立的充分条件、必要条件、充要条件.
(重点)
3.能够利用命题之间的关系判定充要关系或进行充要条件的证明.
(难点)
1.通过充要条件的判断,提升逻辑推理素养.
2.借助充要条件的应用,培养数学运算素养.
学科素养
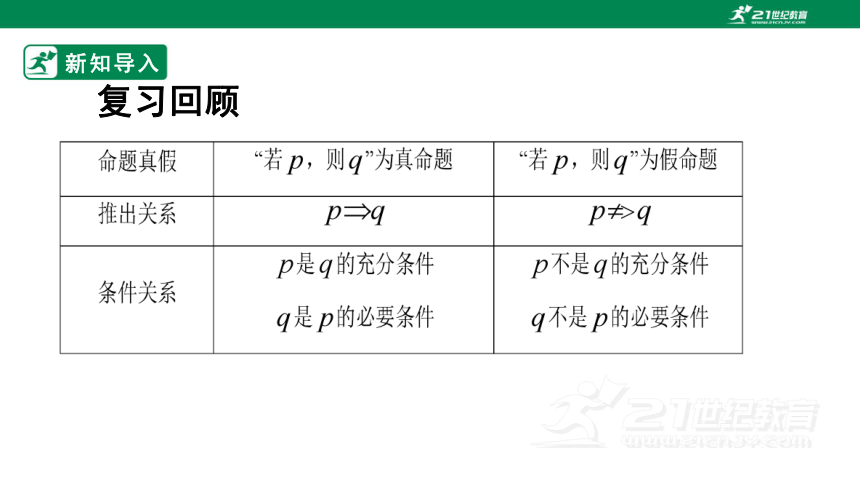
新知导入
复习回顾
新知导入
如果将命题“若p,则q”中的条件p与结论q互换,得到一个新的命题“若p,则q”,称这个命题为原命题的逆命题.
定义:命题“若p,则q”的逆命题为“若q,则p”.
下列“若p,则q”形式的命题中,哪些命题与它们的逆命题都是真命题?
(1)若两个三角形的两角和其中一角所对的边分别相等,则这两个三角形全等;
(2)若两个三角形全等,则这两个三角形的周长相等;
(3)若一元二次方程ax2+bx+c=0有两个不等实数根,则ac<0;
(4)若A∪B是空集,则A与B均是空集 .
上述命题中的命题(1)(4)和它们的逆命题都是真命题;命题(2)是真命题,但它的逆命题是假命题;命题(3)是假命题,但它的逆命题是真命题.
新知导入
如果“若p,则q”和它的逆命题“若q,则p”均是真命题,即
既有p q,又有q p,就记作p q.
此时,p既是q的充分条件,也是q的必要条件,我们说p是q的充分必要条件,简称为充要条件(sufficient and necessary condition).
显然,如果p是q的充要条件,那么q也是q的充要条件.
概括地说,如果p q,那么p与q互为充要条件.
上述命题(1)(4)中的p与q互为充要条件.
通过上面的学习,你能给出“四边形是平行四边形”的充要条件吗
新知讲解
【例1】 下列各题中,哪些p是q的充要条件?
(1)p:四边形是正方形,
q:四边形的对角线互相垂直且平分;
(2)p:两个三角形相似,
q:两个三角形三边成比例;
(3)p:xy>0,
q:x>0,y>0;
(4)p:p=1是一元二次方程ax2+bx+c=0的一个根,
q:a+b+c=0(a≠0)
解:(1)
(2)
(3)
(4)
不是
是
不是
是
新知讲解
充分条件、必要条件及充要条件的理解
1.从定义来看
(3)若p q且q p,则p是q的
(4)若p q且q p,则p是q的
(6)若p q且q p,则p是q的
(5)若p q且q p,则p是q的
q是p的
q是p的
q是p的
q是p的
(1)若p q,则p是q的
q是p的
(2)若p q,则p是q的
q是p的
充分条件
必要条件
不充分条件
不必要条件
充分不必要条件
必要不充分条件
必要不充分条件
充分不必要条件
充要条件
充要条件
既不充分也不必要条件
既不充分也不必要条件
新知讲解
(1)若P Q,则p是q的
(2)若Q P,则p是q的
(3)若P Q,则p是q的
(4)若P Q,则p是q的
(5)若Q P,则p是q的
(6)若P Q且Q P,则p是q的
2.从集合观点来看(命题p:x∈P,命题q:x∈Q)
充分条件.
必要条件.
充要条件.
充分不必要条件.
必要不充分条件.
既不充分也不必要条件.
充分条件、必要条件及充要条件的理解
明辨是非
√
√
【思考辨析】
1.思考辨析(正确的画“√”,错误的画“×”)
(1)当p是q的充要条件时,也可说成q成立当且仅当p成立.( )
(2)符号“ ”表示具有等价性.( )
(3)若p q和q p有一个成立,则p一定不是q的充要条件.( )
(4)数学中的每一个定义都是一个充要条件.( )
√
√
2.设p:“两个三角形相似”,q:“两个三角形的三边对应成比例”,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C. 充要条件 D.既不充分也不必要条件
解:两个三角形相似 两个三角形的三边对应成比例,即p q,故p是q的充要条件.
答案:C
新知讲解
【例2】 用“充分不必要条件、必要不充分条件、充要条件或
既不充分也不必要条件”填空:
(1)“x2-2x-8=0”是“x=-2或x=4”的_________.
(2)“-2(3)“x为自然数”是“x为整数”的 .
(4)“x>3”是“x>5”的 .
充分不必要条件
必要不充分条件
充要条件
既不充分也不必要条件
新知讲解
【例3】 (多选)在下列四个结论中,正确的有( )
A.“x2>4”是“x3<-8”的必要不充分条件
B.在△ABC中,“AB2+AC2=BC2”是“△ABC为直角三角形”的充要条件
C.若a,b∈R,则“a2+b2≠0”是“a,b不为0”的充要条件
D.若a,b∈R,则“a2+b2≠0”是“a,b不全为0”的充要条件
解:对于结论A,由x3<-8 x<-2 x2>4,但是x2>4 x>2或x<-2 x3<-8或x3>8,不一定有x3<-8,故A正确;对于结论D,由a2+b2≠0 a,b不全为0,反之,由a,b不全为0 a2+b2≠0,D正确.
答案:AD
新知讲解
【例4】已知方程x2+(2k-1)x+k2=0,求使方程有两个大于1的实数根的充要条件.
解:方程x2+(2k-1)x+k2=0,则方程有两个大于1的实数根x1,x2:
k<-2.
所以使方程有两个大于1的实根的充要条件是k<-2.
新知讲解
方法归纳
判定充要条件常用方法
初试身受
P22 练习1-2题.
完成下列各题:
(1)命题“x=1且y=2”是命题“x2+y2=2x+4y-5”的( )条件
A.充要 B.充分不必要
C.必要不充分 D.既不充分也不必要
⑵已知是a,b实数,则“a>0且b>0”是“a+b>0且ab>0”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
⑶(多选)设r是p的必要条件,r是q的充分条件,s是r的充分必要条件,s是p的充分条件,则下列说法正确的有( )
A.r是q的必要条件 B.s是q的充分条件
C.s是p的充分必要条件 D.p是q的既不充分也不必要条件
小结归纳
原命题 逆命题 p与q的关系 结论
真 假 p q,但 q p p是q的充分不必要条件;
q是p的必要不充分条件
假 真 q p,但p q p是q的必要不充分条件;
q是p的充分不必要条件
真 真 p q且q p , 即p q p与q互为充要条件
假 假 p q且q p p是q的既不充分也不必要条件;
q是p的既不充分也不必要条件
作业布置
作业:P22-23 习题1.4 第2,3,4,5题
练习:P22 练习 第3题,习题1.4 第1题
尽情享受学习数学的快乐!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第一章 集合与常用逻辑
1.4.2充要条件
教学目标
1.结合具体实例,理解充分条件、必要条件、充要条件的意义.
(重点、难点)
2.会求(判断)某些问题成立的充分条件、必要条件、充要条件.
(重点)
3.能够利用命题之间的关系判定充要关系或进行充要条件的证明.
(难点)
1.通过充要条件的判断,提升逻辑推理素养.
2.借助充要条件的应用,培养数学运算素养.
学科素养
新知导入
复习回顾
新知导入
如果将命题“若p,则q”中的条件p与结论q互换,得到一个新的命题“若p,则q”,称这个命题为原命题的逆命题.
定义:命题“若p,则q”的逆命题为“若q,则p”.
下列“若p,则q”形式的命题中,哪些命题与它们的逆命题都是真命题?
(1)若两个三角形的两角和其中一角所对的边分别相等,则这两个三角形全等;
(2)若两个三角形全等,则这两个三角形的周长相等;
(3)若一元二次方程ax2+bx+c=0有两个不等实数根,则ac<0;
(4)若A∪B是空集,则A与B均是空集 .
上述命题中的命题(1)(4)和它们的逆命题都是真命题;命题(2)是真命题,但它的逆命题是假命题;命题(3)是假命题,但它的逆命题是真命题.
新知导入
如果“若p,则q”和它的逆命题“若q,则p”均是真命题,即
既有p q,又有q p,就记作p q.
此时,p既是q的充分条件,也是q的必要条件,我们说p是q的充分必要条件,简称为充要条件(sufficient and necessary condition).
显然,如果p是q的充要条件,那么q也是q的充要条件.
概括地说,如果p q,那么p与q互为充要条件.
上述命题(1)(4)中的p与q互为充要条件.
通过上面的学习,你能给出“四边形是平行四边形”的充要条件吗
新知讲解
【例1】 下列各题中,哪些p是q的充要条件?
(1)p:四边形是正方形,
q:四边形的对角线互相垂直且平分;
(2)p:两个三角形相似,
q:两个三角形三边成比例;
(3)p:xy>0,
q:x>0,y>0;
(4)p:p=1是一元二次方程ax2+bx+c=0的一个根,
q:a+b+c=0(a≠0)
解:(1)
(2)
(3)
(4)
不是
是
不是
是
新知讲解
充分条件、必要条件及充要条件的理解
1.从定义来看
(3)若p q且q p,则p是q的
(4)若p q且q p,则p是q的
(6)若p q且q p,则p是q的
(5)若p q且q p,则p是q的
q是p的
q是p的
q是p的
q是p的
(1)若p q,则p是q的
q是p的
(2)若p q,则p是q的
q是p的
充分条件
必要条件
不充分条件
不必要条件
充分不必要条件
必要不充分条件
必要不充分条件
充分不必要条件
充要条件
充要条件
既不充分也不必要条件
既不充分也不必要条件
新知讲解
(1)若P Q,则p是q的
(2)若Q P,则p是q的
(3)若P Q,则p是q的
(4)若P Q,则p是q的
(5)若Q P,则p是q的
(6)若P Q且Q P,则p是q的
2.从集合观点来看(命题p:x∈P,命题q:x∈Q)
充分条件.
必要条件.
充要条件.
充分不必要条件.
必要不充分条件.
既不充分也不必要条件.
充分条件、必要条件及充要条件的理解
明辨是非
√
√
【思考辨析】
1.思考辨析(正确的画“√”,错误的画“×”)
(1)当p是q的充要条件时,也可说成q成立当且仅当p成立.( )
(2)符号“ ”表示具有等价性.( )
(3)若p q和q p有一个成立,则p一定不是q的充要条件.( )
(4)数学中的每一个定义都是一个充要条件.( )
√
√
2.设p:“两个三角形相似”,q:“两个三角形的三边对应成比例”,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C. 充要条件 D.既不充分也不必要条件
解:两个三角形相似 两个三角形的三边对应成比例,即p q,故p是q的充要条件.
答案:C
新知讲解
【例2】 用“充分不必要条件、必要不充分条件、充要条件或
既不充分也不必要条件”填空:
(1)“x2-2x-8=0”是“x=-2或x=4”的_________.
(2)“-2
(4)“x>3”是“x>5”的 .
充分不必要条件
必要不充分条件
充要条件
既不充分也不必要条件
新知讲解
【例3】 (多选)在下列四个结论中,正确的有( )
A.“x2>4”是“x3<-8”的必要不充分条件
B.在△ABC中,“AB2+AC2=BC2”是“△ABC为直角三角形”的充要条件
C.若a,b∈R,则“a2+b2≠0”是“a,b不为0”的充要条件
D.若a,b∈R,则“a2+b2≠0”是“a,b不全为0”的充要条件
解:对于结论A,由x3<-8 x<-2 x2>4,但是x2>4 x>2或x<-2 x3<-8或x3>8,不一定有x3<-8,故A正确;对于结论D,由a2+b2≠0 a,b不全为0,反之,由a,b不全为0 a2+b2≠0,D正确.
答案:AD
新知讲解
【例4】已知方程x2+(2k-1)x+k2=0,求使方程有两个大于1的实数根的充要条件.
解:方程x2+(2k-1)x+k2=0,则方程有两个大于1的实数根x1,x2:
k<-2.
所以使方程有两个大于1的实根的充要条件是k<-2.
新知讲解
方法归纳
判定充要条件常用方法
初试身受
P22 练习1-2题.
完成下列各题:
(1)命题“x=1且y=2”是命题“x2+y2=2x+4y-5”的( )条件
A.充要 B.充分不必要
C.必要不充分 D.既不充分也不必要
⑵已知是a,b实数,则“a>0且b>0”是“a+b>0且ab>0”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
⑶(多选)设r是p的必要条件,r是q的充分条件,s是r的充分必要条件,s是p的充分条件,则下列说法正确的有( )
A.r是q的必要条件 B.s是q的充分条件
C.s是p的充分必要条件 D.p是q的既不充分也不必要条件
小结归纳
原命题 逆命题 p与q的关系 结论
真 假 p q,但 q p p是q的充分不必要条件;
q是p的必要不充分条件
假 真 q p,但p q p是q的必要不充分条件;
q是p的充分不必要条件
真 真 p q且q p , 即p q p与q互为充要条件
假 假 p q且q p p是q的既不充分也不必要条件;
q是p的既不充分也不必要条件
作业布置
作业:P22-23 习题1.4 第2,3,4,5题
练习:P22 练习 第3题,习题1.4 第1题
尽情享受学习数学的快乐!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
