19.1.1 第2课时 函数 课件(共18张PPT)
文档属性
| 名称 | 19.1.1 第2课时 函数 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-08 15:52:56 | ||
图片预览





文档简介
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十九章 一次函数
19.1.1 变量与函数
第2课时 函数
理解函数的概念,能准确识别出函数关系中的自变量和函数;
核心素养目标:
理解函数值并会计算,经历由实际问题得出数学概念的过程,发展学生的分析问题,解诀问题的能力;
会用运动的观点观察事物,分析事物,体验生活中的函数关系.
游戏:数青蛙
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿;
三只青蛙三张嘴,六只眼睛十二条腿.
1.青蛙的眼睛数和只数有关系吗?能用数学式子表达吗?
2.青蛙的腿数和只数有关系吗?能用数学式子表达吗?
这里有变化的量吗?如果有,是什么?它们之间有什么关系?
创设情境:
问题3:在上面的4个问题中,两个变量之间的对应关系有什么共同特征?请你再举出一些对应关系具有这种共同特征的例子.
问题1:在上一节课“活动二”的问题(1)~(4)中,是否都存在两个变量?请你用所学知识写出能表示同一个问题中的两个变量之间对应关系的式子.
问题2:在上面的4个问题中,是哪一个量随哪一个量的变化而变化?当一个变量取定一个值时,另一个变量的值是唯一确定的吗?
问题(1)~(4)中都存在两个变量,表示两个变量之间的关系式分别为:
(1)s=60t;(2)y=10x;(3)S=πr?;(4)y=5-x.
以上四个变化过程中,两个变量之间的对应关系都满足:对于一个变量取定一个值时,另一个变量就有唯一确定的值与其对应.
复习引入:
互助探究:
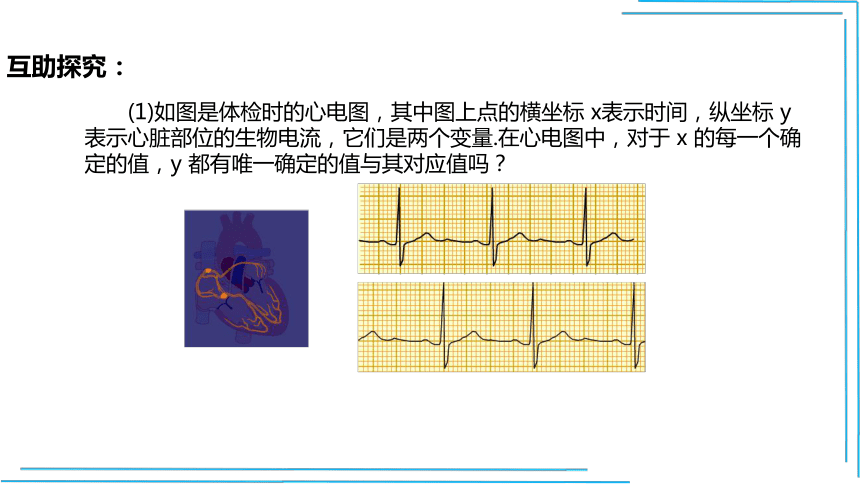
(1)如图是体检时的心电图,其中图上点的横坐标 x表示时间,纵坐标 y 表示心脏部位的生物电流,它们是两个变量.在心电图中,对于 x 的每一个确定的值,y 都有唯一确定的值与其对应值吗?
互助探究:
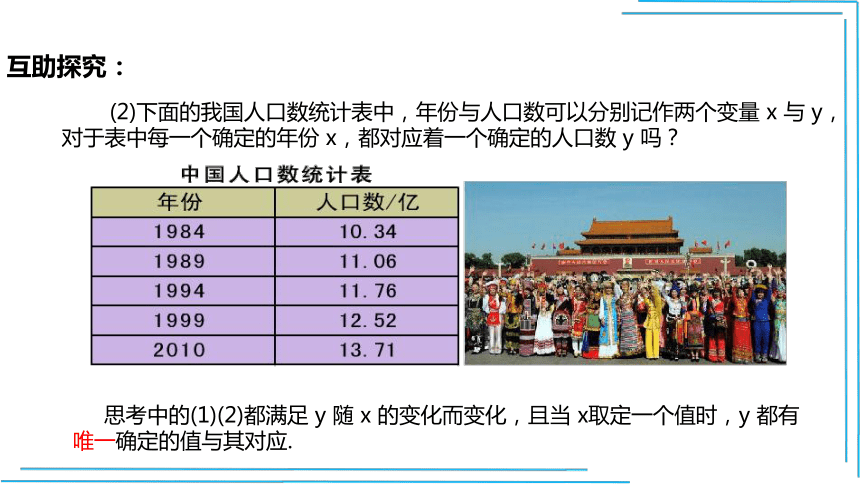
(2)下面的我国人口数统计表中,年份与人口数可以分别记作两个变量 x 与 y,对于表中每一个确定的年份 x,都对应着一个确定的人口数 y 吗?
思考中的(1)(2)都满足 y 随 x 的变化而变化,且当 x取定一个值时,y 都有唯一确定的值与其对应.
生成新知:
一般地,在一个变化过程中,如果有两个变量 x 与y,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
如果当 x = a 时 y = b,那么 b 叫做当自变量的值为 a时的函数值.
在P71的问题(1)~(4)及前面思考(1)(2)的两个变量中,哪些是自变量,哪些是自变量的函数.
当 t =1时,函数值 s =60;
当 t =2时,函数值 s =120;……
函数
(1)如图是体检时的心电图,其中图上点的横坐标 x表示时间,纵坐标 y 表示心脏部位的生物电流,它们是两个变量.在心电图中,对于 x 的每一个确定的值,y 都有唯一确定的值与其对应值吗?
新知应用:
时间 x 是自变量,心脏部位的生物电流 y 是 x 的函数.
(2)下面的我国人口数统计表中,年份与人口数可以分别记作两个变量 x 与 y,对于表中每一个确定的年份 x,都对应着一个确定的人口数 y 吗?
年份 x 是自变量,人口数 y 是x 的函数.
当 x =1984时,函数值 y =10.34;
当 x =1989时,函数值 y =11.06;……
新知应用:
例题精讲:
例1 汽车油箱中有汽油50L,如果不再加油,那么油箱中的油量 y(单位:L)随行驶路程 x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示 y 与 x 的函数关系的式子.
(2)指出自变量 x 的取值范围.
(3)汽车行驶200km时,油箱中还有多少油?
解:(1)行驶路程 x 是自变量,油箱中的油量 y 是 x的函数,它们的关系为 y =50-0.1 x.
0.1 x表示什么意思?
(2)仅从式子 y =50-0.1x 看,x 可以取任意实数.但是考虑到 x 代表的实际意义为行驶路程,因此 x 不能取负数.行驶中的耗油量为0.1x,它不能超过油箱中现有汽油量50,即0.1x≤50。因此,自变量 x 的取值范围是 0≤x≤500.
(3)汽车行驶200km时,油箱中的汽油量是函数 y =50-0.1x 在 x =200时的函数值.将 x =200代入 y =50-0.1x,得y=50-0.1×200=30汽车行驶200km时,油箱中还有30L汽油.
生成新知:
像 y =50-0.1 x 这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用的方法.这种式子叫做函数的解析式.
函数解析式
跟踪练习:
1.下列问题中哪些量是自变量?哪些量是自变量的函数?试写出函数的解析式.
(1)改变正方形的边长x,正方形的面积S随之改变.(2)每分向一水池注水0.1m3,注水量y(单位:m3)随注水时间x(单位:min)的变化而变化.(3)秀水村的耕地面积是106m2,这个村人均占有耕地面 积y(单位:m2)随这个村人数n的变化而变化.(4)水池中有水10L,此后每小时漏水0.05L,水池中的水量V(单位:L)随时间t(单位:h)的变化而变化.
解:
(1)x是自变量,S是x的函数,S=????2.
(2) x是自变量,y是x的函数,y=0.1x.
(3) n是自变量,y是n的函数,y=.106????
(4) t是自变量,V是t的函数,V=10-0.05t.
?
2.梯形的上底长2cm,高3cm,下底长x cm大于上底长但不超过5cm. 写出梯形面积S关于x的函数解析式及自变量x的取值范围.
解:面积S关于x的函数解析式为S=2+????×32,整理得S=3+32 x,自变量x的取值范围是 2<x≤5.
?
跟踪练习:
1.设路程为s,时间为t,速度为v,当v=60时,路程和时间的关系式为 ,这个关系式中, 是常量, 是变量, 是 的函数.
60
s=60t
t和s
s
t
2.油箱中有油30kg,油从管道中匀速流出,1h流完,则油箱中剩余油量Q(kg)与流出时间t(min)之间的函数关系式是 ,自变量t的取值范围是 .
课堂检测:
3.下列各表达式不是表示y是x的函数的是( )
A. B.
C. D.
C
4.求下列函数中自变量x的取值范围:
.
1
.
0
.
-1
x取全体实数
课堂检测:
函数
函数及自变量的概念
函数值
自变量的取值范围
1.使函数解析式有意义
2.符合实际意义
课堂小结:
课后作业:
必做题:81页习题19.1第1、2题
选做题:82页习题19.1第3、4题
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十九章 一次函数
19.1.1 变量与函数
第2课时 函数
理解函数的概念,能准确识别出函数关系中的自变量和函数;
核心素养目标:
理解函数值并会计算,经历由实际问题得出数学概念的过程,发展学生的分析问题,解诀问题的能力;
会用运动的观点观察事物,分析事物,体验生活中的函数关系.
游戏:数青蛙
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿;
三只青蛙三张嘴,六只眼睛十二条腿.
1.青蛙的眼睛数和只数有关系吗?能用数学式子表达吗?
2.青蛙的腿数和只数有关系吗?能用数学式子表达吗?
这里有变化的量吗?如果有,是什么?它们之间有什么关系?
创设情境:
问题3:在上面的4个问题中,两个变量之间的对应关系有什么共同特征?请你再举出一些对应关系具有这种共同特征的例子.
问题1:在上一节课“活动二”的问题(1)~(4)中,是否都存在两个变量?请你用所学知识写出能表示同一个问题中的两个变量之间对应关系的式子.
问题2:在上面的4个问题中,是哪一个量随哪一个量的变化而变化?当一个变量取定一个值时,另一个变量的值是唯一确定的吗?
问题(1)~(4)中都存在两个变量,表示两个变量之间的关系式分别为:
(1)s=60t;(2)y=10x;(3)S=πr?;(4)y=5-x.
以上四个变化过程中,两个变量之间的对应关系都满足:对于一个变量取定一个值时,另一个变量就有唯一确定的值与其对应.
复习引入:
互助探究:
(1)如图是体检时的心电图,其中图上点的横坐标 x表示时间,纵坐标 y 表示心脏部位的生物电流,它们是两个变量.在心电图中,对于 x 的每一个确定的值,y 都有唯一确定的值与其对应值吗?
互助探究:
(2)下面的我国人口数统计表中,年份与人口数可以分别记作两个变量 x 与 y,对于表中每一个确定的年份 x,都对应着一个确定的人口数 y 吗?
思考中的(1)(2)都满足 y 随 x 的变化而变化,且当 x取定一个值时,y 都有唯一确定的值与其对应.
生成新知:
一般地,在一个变化过程中,如果有两个变量 x 与y,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
如果当 x = a 时 y = b,那么 b 叫做当自变量的值为 a时的函数值.
在P71的问题(1)~(4)及前面思考(1)(2)的两个变量中,哪些是自变量,哪些是自变量的函数.
当 t =1时,函数值 s =60;
当 t =2时,函数值 s =120;……
函数
(1)如图是体检时的心电图,其中图上点的横坐标 x表示时间,纵坐标 y 表示心脏部位的生物电流,它们是两个变量.在心电图中,对于 x 的每一个确定的值,y 都有唯一确定的值与其对应值吗?
新知应用:
时间 x 是自变量,心脏部位的生物电流 y 是 x 的函数.
(2)下面的我国人口数统计表中,年份与人口数可以分别记作两个变量 x 与 y,对于表中每一个确定的年份 x,都对应着一个确定的人口数 y 吗?
年份 x 是自变量,人口数 y 是x 的函数.
当 x =1984时,函数值 y =10.34;
当 x =1989时,函数值 y =11.06;……
新知应用:
例题精讲:
例1 汽车油箱中有汽油50L,如果不再加油,那么油箱中的油量 y(单位:L)随行驶路程 x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示 y 与 x 的函数关系的式子.
(2)指出自变量 x 的取值范围.
(3)汽车行驶200km时,油箱中还有多少油?
解:(1)行驶路程 x 是自变量,油箱中的油量 y 是 x的函数,它们的关系为 y =50-0.1 x.
0.1 x表示什么意思?
(2)仅从式子 y =50-0.1x 看,x 可以取任意实数.但是考虑到 x 代表的实际意义为行驶路程,因此 x 不能取负数.行驶中的耗油量为0.1x,它不能超过油箱中现有汽油量50,即0.1x≤50。因此,自变量 x 的取值范围是 0≤x≤500.
(3)汽车行驶200km时,油箱中的汽油量是函数 y =50-0.1x 在 x =200时的函数值.将 x =200代入 y =50-0.1x,得y=50-0.1×200=30汽车行驶200km时,油箱中还有30L汽油.
生成新知:
像 y =50-0.1 x 这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用的方法.这种式子叫做函数的解析式.
函数解析式
跟踪练习:
1.下列问题中哪些量是自变量?哪些量是自变量的函数?试写出函数的解析式.
(1)改变正方形的边长x,正方形的面积S随之改变.(2)每分向一水池注水0.1m3,注水量y(单位:m3)随注水时间x(单位:min)的变化而变化.(3)秀水村的耕地面积是106m2,这个村人均占有耕地面 积y(单位:m2)随这个村人数n的变化而变化.(4)水池中有水10L,此后每小时漏水0.05L,水池中的水量V(单位:L)随时间t(单位:h)的变化而变化.
解:
(1)x是自变量,S是x的函数,S=????2.
(2) x是自变量,y是x的函数,y=0.1x.
(3) n是自变量,y是n的函数,y=.106????
(4) t是自变量,V是t的函数,V=10-0.05t.
?
2.梯形的上底长2cm,高3cm,下底长x cm大于上底长但不超过5cm. 写出梯形面积S关于x的函数解析式及自变量x的取值范围.
解:面积S关于x的函数解析式为S=2+????×32,整理得S=3+32 x,自变量x的取值范围是 2<x≤5.
?
跟踪练习:
1.设路程为s,时间为t,速度为v,当v=60时,路程和时间的关系式为 ,这个关系式中, 是常量, 是变量, 是 的函数.
60
s=60t
t和s
s
t
2.油箱中有油30kg,油从管道中匀速流出,1h流完,则油箱中剩余油量Q(kg)与流出时间t(min)之间的函数关系式是 ,自变量t的取值范围是 .
课堂检测:
3.下列各表达式不是表示y是x的函数的是( )
A. B.
C. D.
C
4.求下列函数中自变量x的取值范围:
.
1
.
0
.
-1
x取全体实数
课堂检测:
函数
函数及自变量的概念
函数值
自变量的取值范围
1.使函数解析式有意义
2.符合实际意义
课堂小结:
课后作业:
必做题:81页习题19.1第1、2题
选做题:82页习题19.1第3、4题
