沪科版八年级数学下册 第17章一元二次方程单元测试(含答案)
文档属性
| 名称 | 沪科版八年级数学下册 第17章一元二次方程单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 50.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-08 14:03:13 | ||
图片预览


文档简介
第17章一元二次方程单元测试
一、选择题(本大题共10小题,每小题3分,共30分).
1.下列选项中,是关于x的一元二次方程的是( )
A.2x+5y=3 B.ax2+bx+c=0 C.2x2+3x=0 D.x2+3x﹣2=x2
2.下列一元二次方程中,有两个相等的实数根的是( )
A.x2﹣2x=0 B.x2+4x=﹣4 C.2x2﹣4x+3=0 D.3x2=5x﹣2
3.若x=1是方程x2﹣ax﹣1=0的一个根,则实数a=( )
A.0 B.﹣1 C.1 D.2
4.若关于x的方程(m﹣4)x2+4x+5=0是一元二次方程,则m的取值范围是( )
A.m<4 B.m≠4 C.m=4 D.m>4
5.电影《长津湖》上映以来,全国票房连创佳绩.据不完全统计,某市第一天票房约2亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达18亿元,将增长率记作x,则方程可以列为( )
A.2+2x+2x2=18 B.2(1+x)2=18
C.(1+x)2=18 D.2+2(1+x)+2(1+x)2=18
6.已知关于x的一元二次方程x2﹣3x+1=0有两个不相等的实数根x1,x2,则x12+x22的值是( )
A.﹣7 B.7 C.2 D.﹣2
7.一元二次方程x2+2x+3=0的根的情况是( )
A.有两个相等的实数根 B.只有一个实数根
C.有两个不相的实数根 D.没有实数根
8.方程x2+2x﹣1=0的两根分别为x1,x2,则下列结论正确的是( )
A.x1+x2=2,x1 x2=1 B.x1+x2=2,x1 x2=﹣1
C.x1+x2=﹣2,x1 x2=﹣1 D.x1+x2=﹣2,x1 x2=1
9.已知xy≠1,且3x2+2021x+6=0,6y2+2021y+3=0,则=( )
A. B.2 C.3 D.9
10.定义:cx2+bx+a=0是一元二次方程ax2+bx+c=0的倒方程,下列四个结论中,错误的是( )
A.如果x=2是x2+2x+c=0的倒方程的解,则c=
B.如果ac<0,那么这两个方程都有两个不相等的实数根
C.如果一元二次方程ax2﹣2x+c=0无解,则它的倒方程也无解
D.如果一元二次方程ax2+bx+c=0有两个不相等的实数根,则它的倒方程也有两个不相等的实数根
二、填空题(本大题共8小题,每小题3分,共24分)
11.已知关于x的一元二次方程x2+mx﹣6=0的一个根是2,求方程的另一根是 .
12.关于x的一元二次方程x2+bx﹣10=0的一个根为2,则b的值为 .
13.2022年端午节期间,合肥某食品专卖店准备了一批粽子,每盒利润为50元,平均每天可卖300盒,经过调查发现每降价1元,可多销售10盒,为了尽快减少库存,决定采取降价措施,专卖店要想平均每天盈利16000元,设每盒粽子降价x元,可列方程 .
14.已知x1,x2是方程x2﹣4x+2=0的两根,则= .
15.若关于x的一元二次方程x2﹣3x+2m=0有一个根为1,则m的值为 .
16.若关于x的一元二次方程x2+2x+a=0有两个不相等实数根,则实数a的取值范围是 .
17.已知a、b实数且满足(a2+b2)2﹣(a2+b2)﹣12=0,则a2+b2的值为 .
18.某种植物的主干长出若干数目的支干,每个支干又长出同样多数目的小分支,主干、支干、小分支一共是43个,则每个支干长出的小分支数目为 .
三、解答题(本大题共6小题,共46分.)
19.用适当的方法解下列一元二次方程
(1)x(3x﹣2)=2(3x﹣2);
(2)2x2﹣4x﹣1=0.
20.已知关于x的一元二次方程x2﹣2x+k+2=0.
(1)若k=﹣6,求此方程的解;
(2)若该方程无实数根,求k的取值范围.
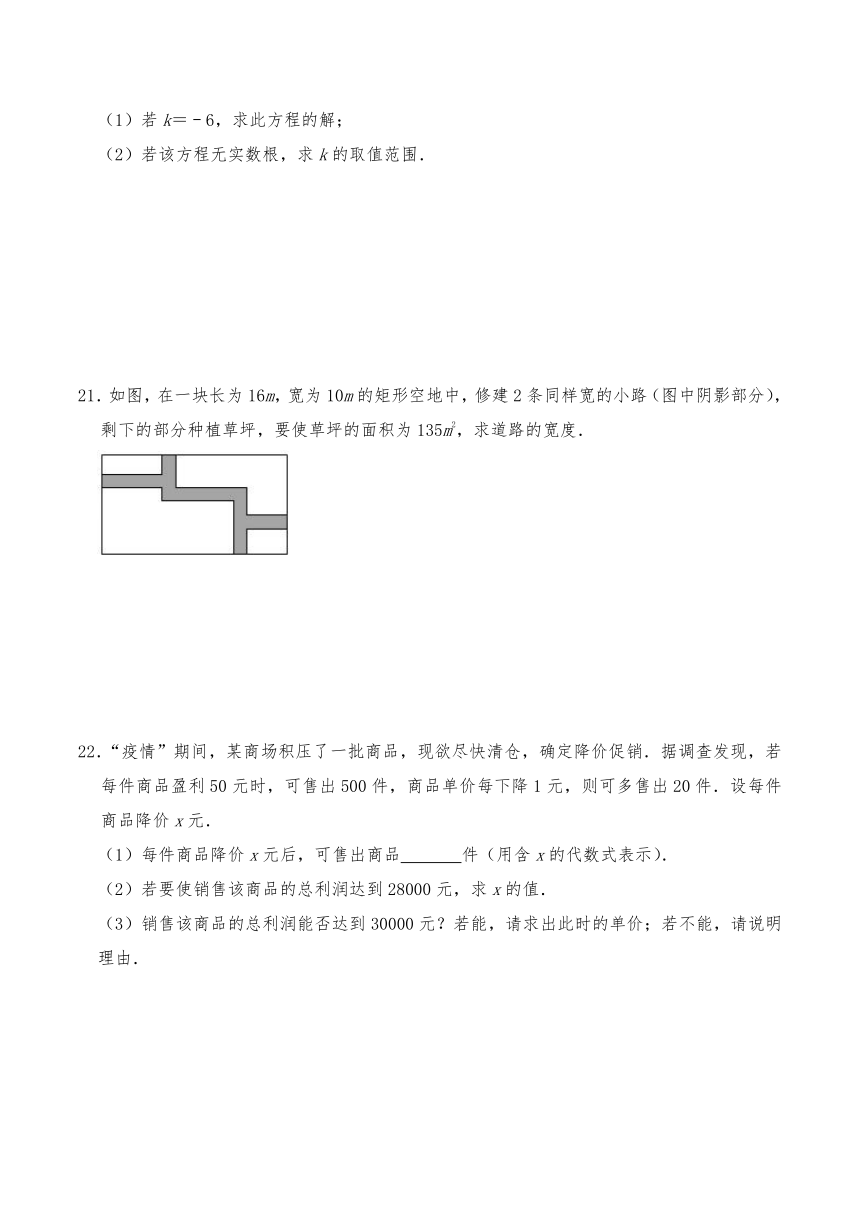
21.如图,在一块长为16m,宽为10m的矩形空地中,修建2条同样宽的小路(图中阴影部分),剩下的部分种植草坪,要使草坪的面积为135m2,求道路的宽度.
22.“疫情”期间,某商场积压了一批商品,现欲尽快清仓,确定降价促销.据调查发现,若每件商品盈利50元时,可售出500件,商品单价每下降1元,则可多售出20件.设每件商品降价x元.
(1)每件商品降价x元后,可售出商品 件(用含x的代数式表示).
(2)若要使销售该商品的总利润达到28000元,求x的值.
(3)销售该商品的总利润能否达到30000元?若能,请求出此时的单价;若不能,请说明理由.
23.阅读理解:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0,
∴(m﹣n)2+(n﹣4)2=0,
∴(m﹣n)2=0且(n﹣4)2=0,
∴m=n=4.
方法应用:
(1)a2+4a+b2+4=0,则a= ,b= ;
(2)已知x+y=8,xy﹣z2﹣4z=20,求(x+y)z的值.
24.如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点…,容易发现10是三角点阵中前4行的点数和.
(1)请用一元二次方程说明:三角点阵中前多少行的点数和是276?
(2)这个三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,说明理由.
答案
一、选择题
C.B.A.B.D.B.D.C.A.D.
二.填空题
11.﹣3. 12.3. 13.(50﹣x)(300+10x)=16000.
14.2. 15.1. 16.a<1. 17.4. 18.6.
三.解答题
19.(1)∵x(3x﹣2)=2(3x﹣2),
∴x(3x﹣2)﹣2(3x﹣2)=0,
则(3x﹣2)(x﹣2)=0,
∴3x﹣2=0或x﹣2=0,
解得x1=,x2=2;
(2)∵2x2﹣4x=1,
∴x2﹣2x=,
则x2﹣2x+1=+1,即(x﹣1)2=,
∴x﹣1=±,
∴x1=,x2=.
20.(1)由题意得:x2﹣2x﹣6+2=0,
x2﹣2x﹣4=0,
x2﹣2x+1=5,
(x﹣1)2=5,
x﹣1=,
x=1,
x1=1+,x2=1﹣;
(2)∵一元二次方程x2﹣2x+k+2=0无解,
∴Δ=(﹣2)2﹣4(k+2)<0,
解得:k>﹣1,
∴k的取值范围为k>﹣1.
21.原图经过平移转化如图所示,
设道路宽为xm,
根据题意,得(16﹣x)(10﹣x)=135,
整理得:x2﹣26x+25=0,
解得:x1=25(不合题意,舍去),x2=1.
则道路宽度为1m.
22.(1)每件商品降价x元后,可售出商品件(500+20x)件;
故答案为:(500+20x);
(2)根据题意得:(50﹣x)(500+20x)=28000,
解得x1=10,x2=15,
∵尽快清仓,
∴x1=10舍去,
答:x的值为15;
(3)(50﹣x)(500+20x)=30000整理得:x2﹣25x+250=0,
b2﹣4ac=625﹣1000<0,方程无解,
所以总利润不能达到30000元.
23.(1)∵a2+4a+b2+4=0,
∴a2+4a+4+b2=0,
∴(a+2)2+b2=0,
∴(a+2)2=0,b2=0,
∴a=﹣2,b=0,
故答案为:﹣2;0;
(2)∵x+y=8,
∴y=8﹣x,
原式变形为x(8﹣x)﹣z2﹣4z=20,
整理得,8x﹣x2﹣z2﹣4z=20,
∴x2﹣8x+16+z2+4z+4=0,
∴(x﹣4)2+(z+2)2=0,
∴(x﹣4)2=0,(z+2)2=0,
∴x=4,z=﹣2,
∴y=8﹣x=4,
∴(x+y)z=.
24.(1)设三角点阵中前x行的点数和是276,
依题意得:1+2+3+……+x=276,
即=276,
整理得:x2+x﹣552=0,
解得:x1=23,x2=﹣24(不合题意,舍去).
答:三角点阵中前23行的点数和是276.
(2)不能,理由如下:
依题意得:1+2+3+……+n=600,
即=600,
整理得:n2+n﹣1200=0,
解得:n1=,n2=.
又∵n为正整数,
∴n1=,n2=均不符合题意,
∴这个三角点阵中前n行的点数和不能是600.
一、选择题(本大题共10小题,每小题3分,共30分).
1.下列选项中,是关于x的一元二次方程的是( )
A.2x+5y=3 B.ax2+bx+c=0 C.2x2+3x=0 D.x2+3x﹣2=x2
2.下列一元二次方程中,有两个相等的实数根的是( )
A.x2﹣2x=0 B.x2+4x=﹣4 C.2x2﹣4x+3=0 D.3x2=5x﹣2
3.若x=1是方程x2﹣ax﹣1=0的一个根,则实数a=( )
A.0 B.﹣1 C.1 D.2
4.若关于x的方程(m﹣4)x2+4x+5=0是一元二次方程,则m的取值范围是( )
A.m<4 B.m≠4 C.m=4 D.m>4
5.电影《长津湖》上映以来,全国票房连创佳绩.据不完全统计,某市第一天票房约2亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达18亿元,将增长率记作x,则方程可以列为( )
A.2+2x+2x2=18 B.2(1+x)2=18
C.(1+x)2=18 D.2+2(1+x)+2(1+x)2=18
6.已知关于x的一元二次方程x2﹣3x+1=0有两个不相等的实数根x1,x2,则x12+x22的值是( )
A.﹣7 B.7 C.2 D.﹣2
7.一元二次方程x2+2x+3=0的根的情况是( )
A.有两个相等的实数根 B.只有一个实数根
C.有两个不相的实数根 D.没有实数根
8.方程x2+2x﹣1=0的两根分别为x1,x2,则下列结论正确的是( )
A.x1+x2=2,x1 x2=1 B.x1+x2=2,x1 x2=﹣1
C.x1+x2=﹣2,x1 x2=﹣1 D.x1+x2=﹣2,x1 x2=1
9.已知xy≠1,且3x2+2021x+6=0,6y2+2021y+3=0,则=( )
A. B.2 C.3 D.9
10.定义:cx2+bx+a=0是一元二次方程ax2+bx+c=0的倒方程,下列四个结论中,错误的是( )
A.如果x=2是x2+2x+c=0的倒方程的解,则c=
B.如果ac<0,那么这两个方程都有两个不相等的实数根
C.如果一元二次方程ax2﹣2x+c=0无解,则它的倒方程也无解
D.如果一元二次方程ax2+bx+c=0有两个不相等的实数根,则它的倒方程也有两个不相等的实数根
二、填空题(本大题共8小题,每小题3分,共24分)
11.已知关于x的一元二次方程x2+mx﹣6=0的一个根是2,求方程的另一根是 .
12.关于x的一元二次方程x2+bx﹣10=0的一个根为2,则b的值为 .
13.2022年端午节期间,合肥某食品专卖店准备了一批粽子,每盒利润为50元,平均每天可卖300盒,经过调查发现每降价1元,可多销售10盒,为了尽快减少库存,决定采取降价措施,专卖店要想平均每天盈利16000元,设每盒粽子降价x元,可列方程 .
14.已知x1,x2是方程x2﹣4x+2=0的两根,则= .
15.若关于x的一元二次方程x2﹣3x+2m=0有一个根为1,则m的值为 .
16.若关于x的一元二次方程x2+2x+a=0有两个不相等实数根,则实数a的取值范围是 .
17.已知a、b实数且满足(a2+b2)2﹣(a2+b2)﹣12=0,则a2+b2的值为 .
18.某种植物的主干长出若干数目的支干,每个支干又长出同样多数目的小分支,主干、支干、小分支一共是43个,则每个支干长出的小分支数目为 .
三、解答题(本大题共6小题,共46分.)
19.用适当的方法解下列一元二次方程
(1)x(3x﹣2)=2(3x﹣2);
(2)2x2﹣4x﹣1=0.
20.已知关于x的一元二次方程x2﹣2x+k+2=0.
(1)若k=﹣6,求此方程的解;
(2)若该方程无实数根,求k的取值范围.
21.如图,在一块长为16m,宽为10m的矩形空地中,修建2条同样宽的小路(图中阴影部分),剩下的部分种植草坪,要使草坪的面积为135m2,求道路的宽度.
22.“疫情”期间,某商场积压了一批商品,现欲尽快清仓,确定降价促销.据调查发现,若每件商品盈利50元时,可售出500件,商品单价每下降1元,则可多售出20件.设每件商品降价x元.
(1)每件商品降价x元后,可售出商品 件(用含x的代数式表示).
(2)若要使销售该商品的总利润达到28000元,求x的值.
(3)销售该商品的总利润能否达到30000元?若能,请求出此时的单价;若不能,请说明理由.
23.阅读理解:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0,
∴(m﹣n)2+(n﹣4)2=0,
∴(m﹣n)2=0且(n﹣4)2=0,
∴m=n=4.
方法应用:
(1)a2+4a+b2+4=0,则a= ,b= ;
(2)已知x+y=8,xy﹣z2﹣4z=20,求(x+y)z的值.
24.如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点…,容易发现10是三角点阵中前4行的点数和.
(1)请用一元二次方程说明:三角点阵中前多少行的点数和是276?
(2)这个三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,说明理由.
答案
一、选择题
C.B.A.B.D.B.D.C.A.D.
二.填空题
11.﹣3. 12.3. 13.(50﹣x)(300+10x)=16000.
14.2. 15.1. 16.a<1. 17.4. 18.6.
三.解答题
19.(1)∵x(3x﹣2)=2(3x﹣2),
∴x(3x﹣2)﹣2(3x﹣2)=0,
则(3x﹣2)(x﹣2)=0,
∴3x﹣2=0或x﹣2=0,
解得x1=,x2=2;
(2)∵2x2﹣4x=1,
∴x2﹣2x=,
则x2﹣2x+1=+1,即(x﹣1)2=,
∴x﹣1=±,
∴x1=,x2=.
20.(1)由题意得:x2﹣2x﹣6+2=0,
x2﹣2x﹣4=0,
x2﹣2x+1=5,
(x﹣1)2=5,
x﹣1=,
x=1,
x1=1+,x2=1﹣;
(2)∵一元二次方程x2﹣2x+k+2=0无解,
∴Δ=(﹣2)2﹣4(k+2)<0,
解得:k>﹣1,
∴k的取值范围为k>﹣1.
21.原图经过平移转化如图所示,
设道路宽为xm,
根据题意,得(16﹣x)(10﹣x)=135,
整理得:x2﹣26x+25=0,
解得:x1=25(不合题意,舍去),x2=1.
则道路宽度为1m.
22.(1)每件商品降价x元后,可售出商品件(500+20x)件;
故答案为:(500+20x);
(2)根据题意得:(50﹣x)(500+20x)=28000,
解得x1=10,x2=15,
∵尽快清仓,
∴x1=10舍去,
答:x的值为15;
(3)(50﹣x)(500+20x)=30000整理得:x2﹣25x+250=0,
b2﹣4ac=625﹣1000<0,方程无解,
所以总利润不能达到30000元.
23.(1)∵a2+4a+b2+4=0,
∴a2+4a+4+b2=0,
∴(a+2)2+b2=0,
∴(a+2)2=0,b2=0,
∴a=﹣2,b=0,
故答案为:﹣2;0;
(2)∵x+y=8,
∴y=8﹣x,
原式变形为x(8﹣x)﹣z2﹣4z=20,
整理得,8x﹣x2﹣z2﹣4z=20,
∴x2﹣8x+16+z2+4z+4=0,
∴(x﹣4)2+(z+2)2=0,
∴(x﹣4)2=0,(z+2)2=0,
∴x=4,z=﹣2,
∴y=8﹣x=4,
∴(x+y)z=.
24.(1)设三角点阵中前x行的点数和是276,
依题意得:1+2+3+……+x=276,
即=276,
整理得:x2+x﹣552=0,
解得:x1=23,x2=﹣24(不合题意,舍去).
答:三角点阵中前23行的点数和是276.
(2)不能,理由如下:
依题意得:1+2+3+……+n=600,
即=600,
整理得:n2+n﹣1200=0,
解得:n1=,n2=.
又∵n为正整数,
∴n1=,n2=均不符合题意,
∴这个三角点阵中前n行的点数和不能是600.
