沪科版八年级数学下册第18章勾股定理单元测试(含答案)
文档属性
| 名称 | 沪科版八年级数学下册第18章勾股定理单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 683.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-08 14:04:14 | ||
图片预览



文档简介
第18章勾股定理单元测试
一、选择题(本大题共10小题,每小题3分,共30分)
1.直角三角形两直角边长度为5,12,则斜边上的高
A.6 B.8 C. D.
2.已知,,是的三条边,则下列条件不能判定是直角三角形的是
A.,, B.
C. D.
3.下列四组数中,是勾股数的是
A.0.3,0.4,0.5 B.,, C.30,40,50 D.,,
4.两只小鼹鼠在地下从同一处开始打洞,一只朝北面挖,每分钟挖,另一只朝东面挖,每分钟挖,10分钟之后两只小鼹鼠相距
A. B. C. D.
5.已知,为正数,且,如果以,的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为
A.10 B.100 C.14 D.196
6.如图有一个水池,水面的宽为16尺,在水池的中央有一根芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个芦苇的高度是
A.26尺 B.24尺 C.17尺 D.15尺
7.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,大正方形面积为64,小正方形面积为9,若用,表示直角三角形的两直角边长,请观察图案,下列关系式中不正确的是
A. B. C. D.
8.如图,中,,若,则正方形和正方形的面积和为
A. B. C. D.无法计算
9.已知,如图长方形中,,,将此长方形折叠,使点与点重合,折痕为,则的面积为
A. B. C. D.
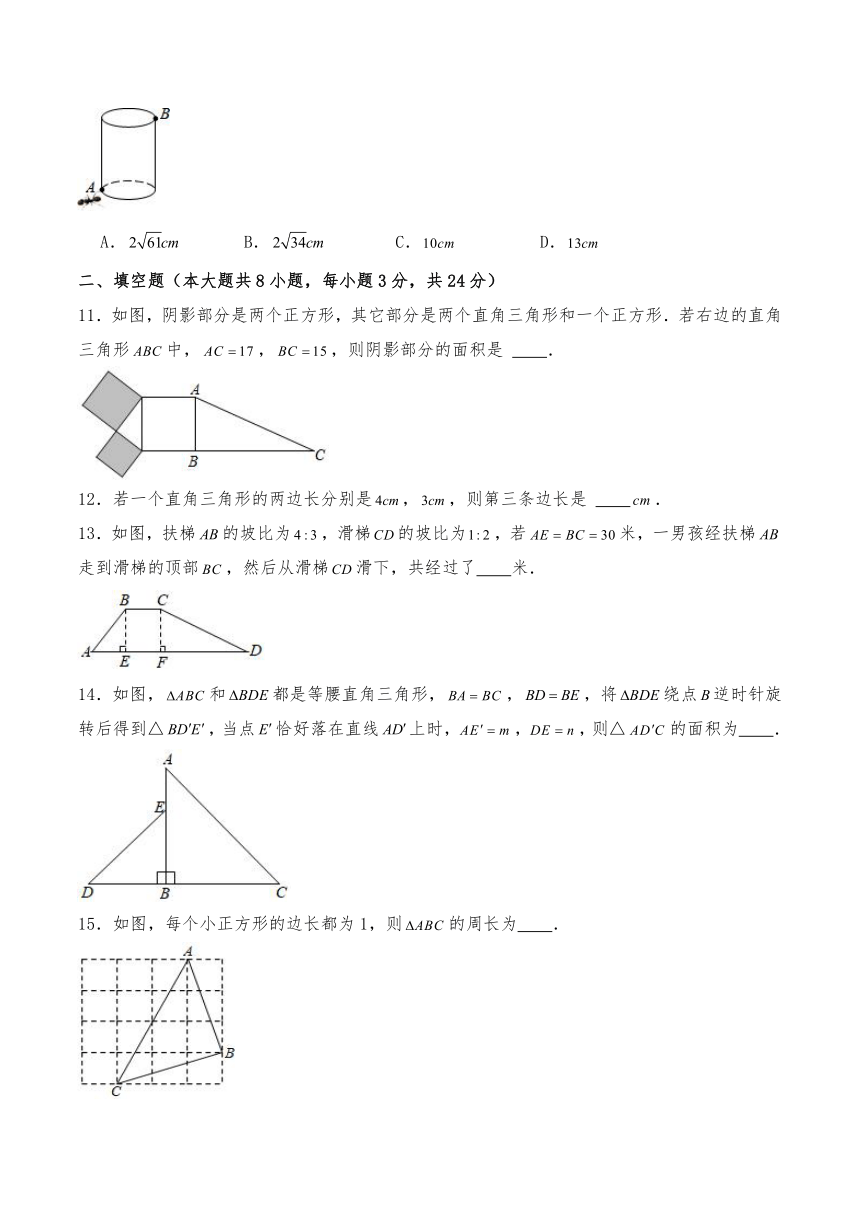
10.如图有一个圆柱,它的高等于,底面上圆的周长等于,在圆柱下底面的点有一只蚂蚁,它想吃到上底面上与点相对的点处的食物,沿圆柱侧面爬行的最短路程是
A. B. C. D.
二、填空题(本大题共8小题,每小题3分,共24分)
11.如图,阴影部分是两个正方形,其它部分是两个直角三角形和一个正方形.若右边的直角三角形中,,,则阴影部分的面积是 .
12.若一个直角三角形的两边长分别是,,则第三条边长是 .
13.如图,扶梯的坡比为,滑梯的坡比为,若米,一男孩经扶梯走到滑梯的顶部,然后从滑梯滑下,共经过了 米.
14.如图,和都是等腰直角三角形,,,将绕点逆时针旋转后得到△,当点恰好落在直线上时,,,则△的面积为 .
15.如图,每个小正方形的边长都为1,则的周长为 .
16.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点的位置,问船向岸边移动了 米.(假设绳子是直的)
17.如图,已知在中,,分别以,,为直径作半圆,面积分别记为,,,若,则等于 .
18.如图1,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.在此图形中连接四条线段得到如图2的图案,记阴影部分的面积为,空白部分的面积为,大正方形的边长为,小正方形的边长为,若,则的值为 .
三、解答题(本大题共6小题,共46分.)
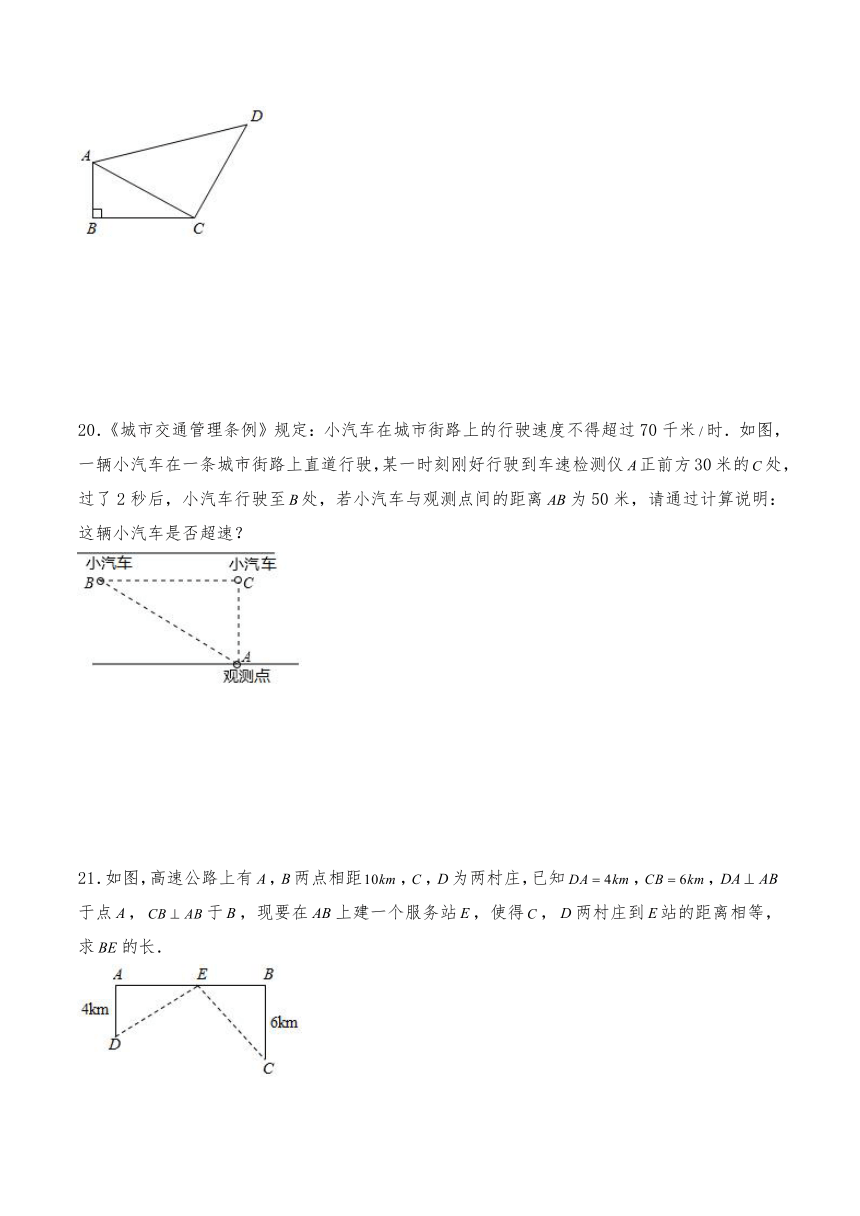
19.如图,在四边形中,,,,,,求四边形的面积.
20.《城市交通管理条例》规定:小汽车在城市街路上的行驶速度不得超过70千米时.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到车速检测仪正前方30米的处,过了2秒后,小汽车行驶至处,若小汽车与观测点间的距离为50米,请通过计算说明:这辆小汽车是否超速?
21.如图,高速公路上有,两点相距,,为两村庄,已知,,于点,于,现要在上建一个服务站,使得,两村庄到站的距离相等,求的长.
22.如图,在中,点是边的中点,交于点,且.
(1)求证:;
(2)若,,求的长度.
23.如图,已知一艘轮船以20海里时的速度由西向东航行,途中接到台风警报,台风中心正以40海里时的速度由南向北移动,距台风中心海里的圆形区域(包括边界)都属台风区.当轮船到处时,测得台风中心移到位于点正南方向处,且海里,若这艘轮船自处按原速度继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,请说明理由.
24.(1)如图1,已知是的中线,,把沿所在直线对折,点落在点的位置(如图,则等于 度.
(2)如图2,有一直角三角形纸片,两直角边,,将直角边沿直线折叠,使它落在斜边上,且与重合,求的长.
答案
一、选择题
..........
二.填空题
11.64. 12.5或. 13.. 14.或.
15.. 16.9. 17.. 18..
三.解答题
19.,,,
,
在中,,
是直角三角形,且,
.
故四边形的面积为.
20.由勾股定理可得:,
40米千米,
2秒小时.
.
所以超速了.
21.设,则,
由勾股定理得:
在中,
,
在中,
,
由题意可知:,
所以:,
解得:.
所以,的长是.
22.(1)证明:连结,
是的中点,,
,
,
,
,
是直角三角形,即;
(2)解是的中点,,
,
,,
,
在中,,
,
,
解得:,
的长为.
23.设途中会遇到台风,且最初遇到的时间为,此时轮船位于处,台风中心移到处,连接,
则,
,
.
,
解得,(不合题意舍去).
答:最初遇到的时间为.
24.(1)依题意,得,即,
又,为的中线,
,即,为等腰直角三角形,
;
(2)令,则,
由于是直角三角形且是折叠,所以,,
,,因为,
故在中运用勾股定理得:
,
,解得,即.
一、选择题(本大题共10小题,每小题3分,共30分)
1.直角三角形两直角边长度为5,12,则斜边上的高
A.6 B.8 C. D.
2.已知,,是的三条边,则下列条件不能判定是直角三角形的是
A.,, B.
C. D.
3.下列四组数中,是勾股数的是
A.0.3,0.4,0.5 B.,, C.30,40,50 D.,,
4.两只小鼹鼠在地下从同一处开始打洞,一只朝北面挖,每分钟挖,另一只朝东面挖,每分钟挖,10分钟之后两只小鼹鼠相距
A. B. C. D.
5.已知,为正数,且,如果以,的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为
A.10 B.100 C.14 D.196
6.如图有一个水池,水面的宽为16尺,在水池的中央有一根芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个芦苇的高度是
A.26尺 B.24尺 C.17尺 D.15尺
7.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,大正方形面积为64,小正方形面积为9,若用,表示直角三角形的两直角边长,请观察图案,下列关系式中不正确的是
A. B. C. D.
8.如图,中,,若,则正方形和正方形的面积和为
A. B. C. D.无法计算
9.已知,如图长方形中,,,将此长方形折叠,使点与点重合,折痕为,则的面积为
A. B. C. D.
10.如图有一个圆柱,它的高等于,底面上圆的周长等于,在圆柱下底面的点有一只蚂蚁,它想吃到上底面上与点相对的点处的食物,沿圆柱侧面爬行的最短路程是
A. B. C. D.
二、填空题(本大题共8小题,每小题3分,共24分)
11.如图,阴影部分是两个正方形,其它部分是两个直角三角形和一个正方形.若右边的直角三角形中,,,则阴影部分的面积是 .
12.若一个直角三角形的两边长分别是,,则第三条边长是 .
13.如图,扶梯的坡比为,滑梯的坡比为,若米,一男孩经扶梯走到滑梯的顶部,然后从滑梯滑下,共经过了 米.
14.如图,和都是等腰直角三角形,,,将绕点逆时针旋转后得到△,当点恰好落在直线上时,,,则△的面积为 .
15.如图,每个小正方形的边长都为1,则的周长为 .
16.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点的位置,问船向岸边移动了 米.(假设绳子是直的)
17.如图,已知在中,,分别以,,为直径作半圆,面积分别记为,,,若,则等于 .
18.如图1,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.在此图形中连接四条线段得到如图2的图案,记阴影部分的面积为,空白部分的面积为,大正方形的边长为,小正方形的边长为,若,则的值为 .
三、解答题(本大题共6小题,共46分.)
19.如图,在四边形中,,,,,,求四边形的面积.
20.《城市交通管理条例》规定:小汽车在城市街路上的行驶速度不得超过70千米时.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到车速检测仪正前方30米的处,过了2秒后,小汽车行驶至处,若小汽车与观测点间的距离为50米,请通过计算说明:这辆小汽车是否超速?
21.如图,高速公路上有,两点相距,,为两村庄,已知,,于点,于,现要在上建一个服务站,使得,两村庄到站的距离相等,求的长.
22.如图,在中,点是边的中点,交于点,且.
(1)求证:;
(2)若,,求的长度.
23.如图,已知一艘轮船以20海里时的速度由西向东航行,途中接到台风警报,台风中心正以40海里时的速度由南向北移动,距台风中心海里的圆形区域(包括边界)都属台风区.当轮船到处时,测得台风中心移到位于点正南方向处,且海里,若这艘轮船自处按原速度继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,请说明理由.
24.(1)如图1,已知是的中线,,把沿所在直线对折,点落在点的位置(如图,则等于 度.
(2)如图2,有一直角三角形纸片,两直角边,,将直角边沿直线折叠,使它落在斜边上,且与重合,求的长.
答案
一、选择题
..........
二.填空题
11.64. 12.5或. 13.. 14.或.
15.. 16.9. 17.. 18..
三.解答题
19.,,,
,
在中,,
是直角三角形,且,
.
故四边形的面积为.
20.由勾股定理可得:,
40米千米,
2秒小时.
.
所以超速了.
21.设,则,
由勾股定理得:
在中,
,
在中,
,
由题意可知:,
所以:,
解得:.
所以,的长是.
22.(1)证明:连结,
是的中点,,
,
,
,
,
是直角三角形,即;
(2)解是的中点,,
,
,,
,
在中,,
,
,
解得:,
的长为.
23.设途中会遇到台风,且最初遇到的时间为,此时轮船位于处,台风中心移到处,连接,
则,
,
.
,
解得,(不合题意舍去).
答:最初遇到的时间为.
24.(1)依题意,得,即,
又,为的中线,
,即,为等腰直角三角形,
;
(2)令,则,
由于是直角三角形且是折叠,所以,,
,,因为,
故在中运用勾股定理得:
,
,解得,即.
