沪科版八年级数学下册第18章勾股定理单元测试卷(含答案)
文档属性
| 名称 | 沪科版八年级数学下册第18章勾股定理单元测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 776.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-08 14:08:12 | ||
图片预览


文档简介
第18章勾股定理单元测试卷
一、选择题(本大题共10小题,每小题3分,共30分).
1.由下列条件不能判定为直角三角形的是
A. B.
C.,, D.
2.下列各组数中,哪一组是勾股数
A.1,2,4 B.1,3,5 C.3,4,7 D.5,12,13
3.“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的大正方形.每个直角三角形的两条直角边的长分别是和,则中间小正方形的面积是
A. B. C. D.
4.已知中,、、分别是、、的对边,下列条件不能判断是直角三角形的是
A. B.,,
C. D.
5.如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,这根芦苇的长度为 尺.
A.10 B.12 C.13 D.14
6.一个直角三角形两直角边长为6和8,三角形内一点到各边距离相等,那么这个距离为
A.1 B.2 C.3 D.4
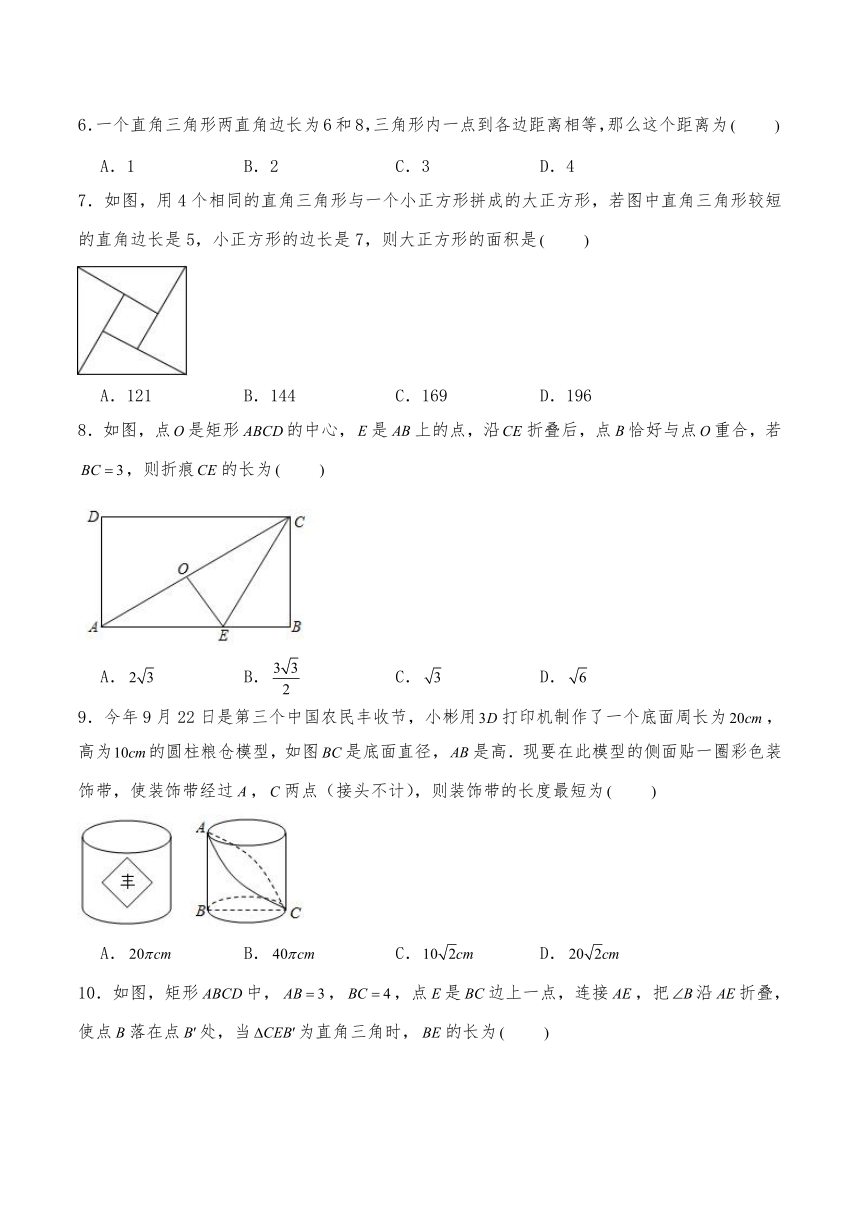
7.如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边长是5,小正方形的边长是7,则大正方形的面积是
A.121 B.144 C.169 D.196
8.如图,点是矩形的中心,是上的点,沿折叠后,点恰好与点重合,若,则折痕的长为
A. B. C. D.
9.今年9月22日是第三个中国农民丰收节,小彬用打印机制作了一个底面周长为,高为的圆柱粮仓模型,如图是底面直径,是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过,两点(接头不计),则装饰带的长度最短为
A. B. C. D.
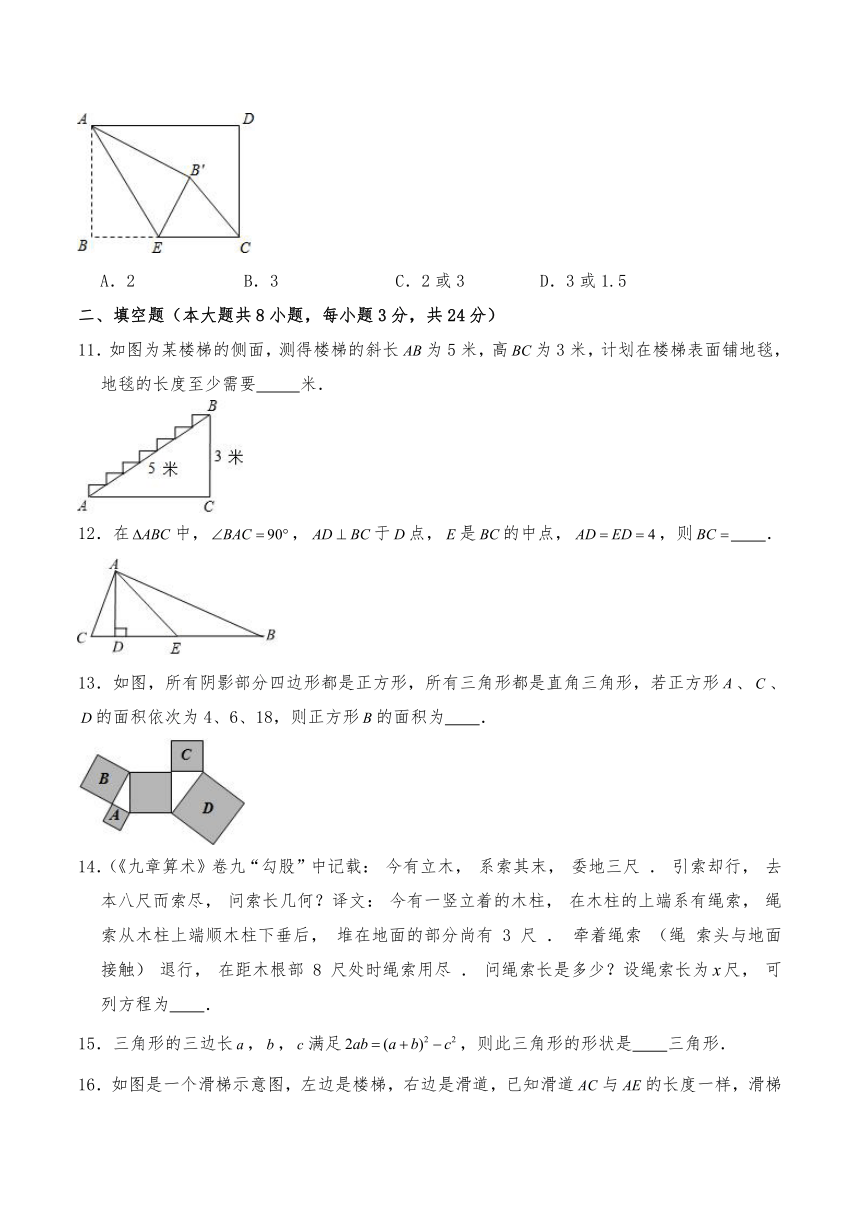
10.如图,矩形中,,,点是边上一点,连接,把沿折叠,使点落在点处,当为直角三角时,的长为
A.2 B.3 C.2或3 D.3或1.5
二、填空题(本大题共8小题,每小题3分,共24分)
11.如图为某楼梯的侧面,测得楼梯的斜长为5米,高为3米,计划在楼梯表面铺地毯,地毯的长度至少需要 米.
12.在中,,于点,是的中点,,则 .
13.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形、、的面积依次为4、6、18,则正方形的面积为 .
14.(《九章算术》卷九“勾股”中记载: 今有立木, 系索其末, 委地三尺 . 引索却行, 去本八尺而索尽, 问索长几何?译文: 今有一竖立着的木柱, 在木柱的上端系有绳索, 绳索从木柱上端顺木柱下垂后, 堆在地面的部分尚有 3 尺 . 牵着绳索 (绳 索头与地面接触) 退行, 在距木根部 8 尺处时绳索用尽 . 问绳索长是多少?设绳索长为尺, 可列方程为 .
15.三角形的三边长,,满足,则此三角形的形状是 三角形.
16.如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道与的长度一样,滑梯的高度,.则滑道的长度为 .
17.如图是高空秋千的示意图,小明从起始位置点处绕着点经过最低点.最终荡到最高点处,若,点与点的高度差米,水平距离米,则点与点的高度差为 米.
18.2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图,且大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边为,较长直角边为.如果将四个全等的直角三角形按如图2的形式摆放,那么图2中最大的正方形的面积为 .
三、解答题(本大题共6小题,共46分.)
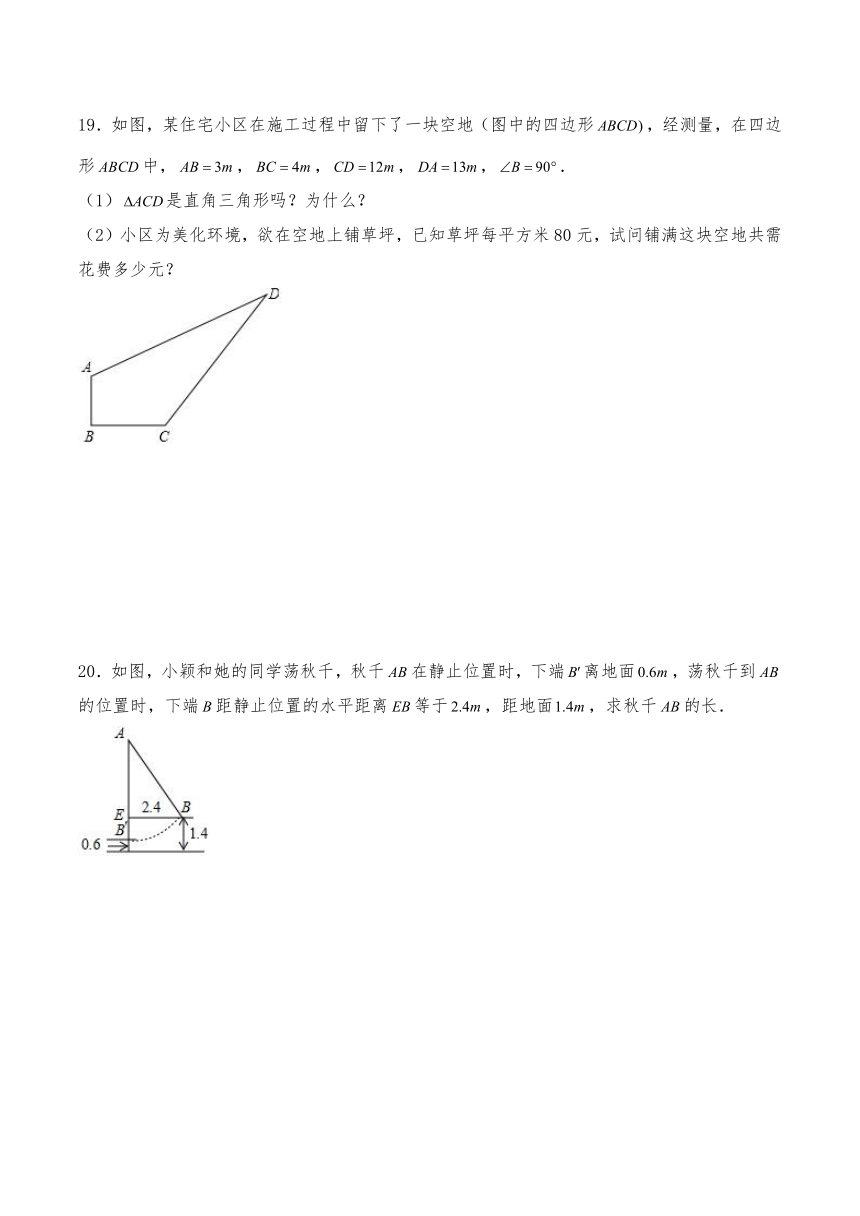
19.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形,经测量,在四边形中,,,,,.
(1)是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米80元,试问铺满这块空地共需花费多少元?
20.如图,小颖和她的同学荡秋千,秋千在静止位置时,下端离地面,荡秋千到的位置时,下端距静止位置的水平距离等于,距地面,求秋千的长.
21.如图,已知和是等腰直角三角形,,点在上.
(1)求证:;
(2)若,求的值.
22.如图,把长方形纸片沿折叠,使点落在边上的点处,点落在点处.
(1)试说明;
(2)设,,,试猜想,,之间的关系,并说明理由.
23.中,,,边上的高长为12.求的长.
24.(1)教材在探索平方差公式时利用了面积法,面积法可以帮助我们直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为,较小的直角边长都为,斜边长都为,大正方形的面积可以表示为,也可以表示为,所以,即.由此推导出重要的勾股定理:如果直角三角形两条直角边长为,,斜边长为,则.图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)试用勾股定理解决以下问题:
如果直角三角形的两直角边长为3和4,则斜边上的高为 .
(3)试构造一个图形,使它的面积能够解释,画在上面的网格中,并标出字母,所表示的线段.
答案
一、选择题
..........
二.填空题
11.7. 12.. 13.8. 14.
15.直角. 16.8.5. 17.4.5. 18.27.
三.解答题
19.(1)如图,连接,
在中,,,,
,
在中,,,
,
是直角三角形,;
(2),,
,
费用(元.
答:铺满这块空地共需花费2880元.
20.设,由题意可得出:,
则,
在中,,
解得:,
答:秋千的长为.
21.(1)是等腰直角三角形,
,,,
同理可得:,,,
,
在与中,
,,,
.
(2)是等腰直角三角形,
,
,
,,
,
,
.
22.(1)证明:由折叠的性质得:,,
在长方形纸片中,,
,
,
,
.
(2)解:,,之间的关系是.理由如下:
由(1)知,
由折叠的性质得:,,.
在△中,,
,
.
23.分两种情况:
(1)如图,锐角中,,,边上高,
在中,,,由勾股定理得
,
,
在中,,,由勾股定理得
,
,
的长为;
(2)钝角中,,,边上高,
在中,,由勾股定理得
,
,
在中,,由勾股定理得
,
,
的长为.
综上,的长为14或4.
24.(1)梯形的面积为,
也利用表示为,
,
即;
(2)直角三角形的两直角边分别为3,4,
斜边为5,
设斜边上的高为,直角三角形的面积为,
,
故答案为;
(3)图形面积为:,
边长为,
由此可画出的图形为:
一、选择题(本大题共10小题,每小题3分,共30分).
1.由下列条件不能判定为直角三角形的是
A. B.
C.,, D.
2.下列各组数中,哪一组是勾股数
A.1,2,4 B.1,3,5 C.3,4,7 D.5,12,13
3.“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的大正方形.每个直角三角形的两条直角边的长分别是和,则中间小正方形的面积是
A. B. C. D.
4.已知中,、、分别是、、的对边,下列条件不能判断是直角三角形的是
A. B.,,
C. D.
5.如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,这根芦苇的长度为 尺.
A.10 B.12 C.13 D.14
6.一个直角三角形两直角边长为6和8,三角形内一点到各边距离相等,那么这个距离为
A.1 B.2 C.3 D.4
7.如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边长是5,小正方形的边长是7,则大正方形的面积是
A.121 B.144 C.169 D.196
8.如图,点是矩形的中心,是上的点,沿折叠后,点恰好与点重合,若,则折痕的长为
A. B. C. D.
9.今年9月22日是第三个中国农民丰收节,小彬用打印机制作了一个底面周长为,高为的圆柱粮仓模型,如图是底面直径,是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过,两点(接头不计),则装饰带的长度最短为
A. B. C. D.
10.如图,矩形中,,,点是边上一点,连接,把沿折叠,使点落在点处,当为直角三角时,的长为
A.2 B.3 C.2或3 D.3或1.5
二、填空题(本大题共8小题,每小题3分,共24分)
11.如图为某楼梯的侧面,测得楼梯的斜长为5米,高为3米,计划在楼梯表面铺地毯,地毯的长度至少需要 米.
12.在中,,于点,是的中点,,则 .
13.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形、、的面积依次为4、6、18,则正方形的面积为 .
14.(《九章算术》卷九“勾股”中记载: 今有立木, 系索其末, 委地三尺 . 引索却行, 去本八尺而索尽, 问索长几何?译文: 今有一竖立着的木柱, 在木柱的上端系有绳索, 绳索从木柱上端顺木柱下垂后, 堆在地面的部分尚有 3 尺 . 牵着绳索 (绳 索头与地面接触) 退行, 在距木根部 8 尺处时绳索用尽 . 问绳索长是多少?设绳索长为尺, 可列方程为 .
15.三角形的三边长,,满足,则此三角形的形状是 三角形.
16.如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道与的长度一样,滑梯的高度,.则滑道的长度为 .
17.如图是高空秋千的示意图,小明从起始位置点处绕着点经过最低点.最终荡到最高点处,若,点与点的高度差米,水平距离米,则点与点的高度差为 米.
18.2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图,且大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边为,较长直角边为.如果将四个全等的直角三角形按如图2的形式摆放,那么图2中最大的正方形的面积为 .
三、解答题(本大题共6小题,共46分.)
19.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形,经测量,在四边形中,,,,,.
(1)是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米80元,试问铺满这块空地共需花费多少元?
20.如图,小颖和她的同学荡秋千,秋千在静止位置时,下端离地面,荡秋千到的位置时,下端距静止位置的水平距离等于,距地面,求秋千的长.
21.如图,已知和是等腰直角三角形,,点在上.
(1)求证:;
(2)若,求的值.
22.如图,把长方形纸片沿折叠,使点落在边上的点处,点落在点处.
(1)试说明;
(2)设,,,试猜想,,之间的关系,并说明理由.
23.中,,,边上的高长为12.求的长.
24.(1)教材在探索平方差公式时利用了面积法,面积法可以帮助我们直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为,较小的直角边长都为,斜边长都为,大正方形的面积可以表示为,也可以表示为,所以,即.由此推导出重要的勾股定理:如果直角三角形两条直角边长为,,斜边长为,则.图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)试用勾股定理解决以下问题:
如果直角三角形的两直角边长为3和4,则斜边上的高为 .
(3)试构造一个图形,使它的面积能够解释,画在上面的网格中,并标出字母,所表示的线段.
答案
一、选择题
..........
二.填空题
11.7. 12.. 13.8. 14.
15.直角. 16.8.5. 17.4.5. 18.27.
三.解答题
19.(1)如图,连接,
在中,,,,
,
在中,,,
,
是直角三角形,;
(2),,
,
费用(元.
答:铺满这块空地共需花费2880元.
20.设,由题意可得出:,
则,
在中,,
解得:,
答:秋千的长为.
21.(1)是等腰直角三角形,
,,,
同理可得:,,,
,
在与中,
,,,
.
(2)是等腰直角三角形,
,
,
,,
,
,
.
22.(1)证明:由折叠的性质得:,,
在长方形纸片中,,
,
,
,
.
(2)解:,,之间的关系是.理由如下:
由(1)知,
由折叠的性质得:,,.
在△中,,
,
.
23.分两种情况:
(1)如图,锐角中,,,边上高,
在中,,,由勾股定理得
,
,
在中,,,由勾股定理得
,
,
的长为;
(2)钝角中,,,边上高,
在中,,由勾股定理得
,
,
在中,,由勾股定理得
,
,
的长为.
综上,的长为14或4.
24.(1)梯形的面积为,
也利用表示为,
,
即;
(2)直角三角形的两直角边分别为3,4,
斜边为5,
设斜边上的高为,直角三角形的面积为,
,
故答案为;
(3)图形面积为:,
边长为,
由此可画出的图形为:
