沪科版八年级数学下册18章勾股定理的应用试题(含答案)
文档属性
| 名称 | 沪科版八年级数学下册18章勾股定理的应用试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-08 14:57:53 | ||
图片预览



文档简介
勾股定理的应用
一、解答题
1.如图,把一块直角三角形土地划出一个三角形后,测得米,米,米,米.
(1)求证:;
(2)求图中阴影部分土地的面积.
2.如图,城气象台测得台风中心在城正西方向的处,以每小时的速度向北偏东的方向移动,距台风中心的范围内是受台风影响的区域.
(1)城是否受到这次台风的影响?为什么?
(2)若城受到这次台风的影响,那么城遭受这次台风影响有多长时间?
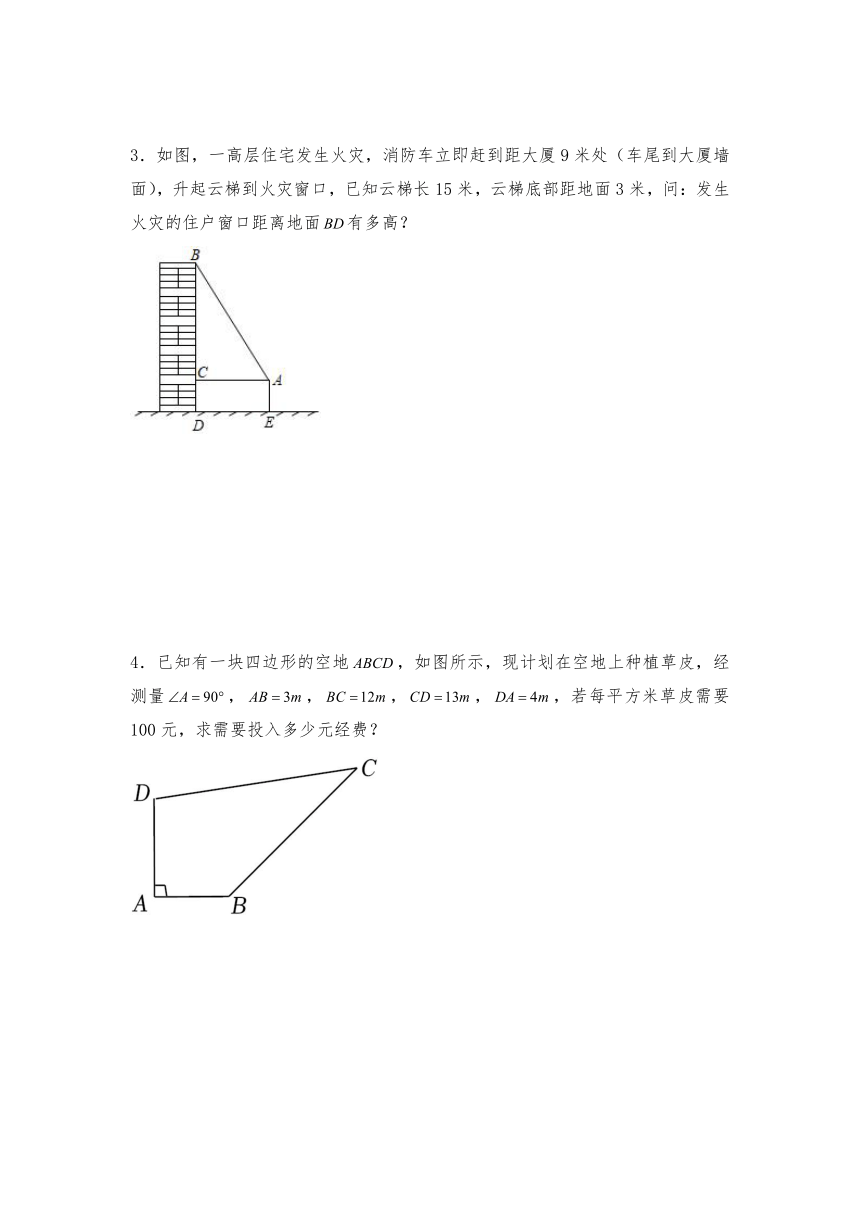
3.如图,一高层住宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面3米,问:发生火灾的住户窗口距离地面有多高?
4.已知有一块四边形的空地,如图所示,现计划在空地上种植草皮,经测量,,,,,若每平方米草皮需要100元,求需要投入多少元经费?
5.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根四尺,问折者高几何?”翻译成数学问题是:如图所示,中,,,,求的长.
6.如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度.于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(如图为示意图).请你帮小旭求出风筝距离地面的高度.
7.如图,湖的两岸有,两点,在与成直角的方向上的点处测得米,米.
(1)求,两点间的距离;
(2)求点到直线的距离.
8.如图,秋千静止的时候,踏板离地高一尺尺),将它往前推进两步尺),此时踏板升高离地五尺尺),求秋千绳索或的长度.
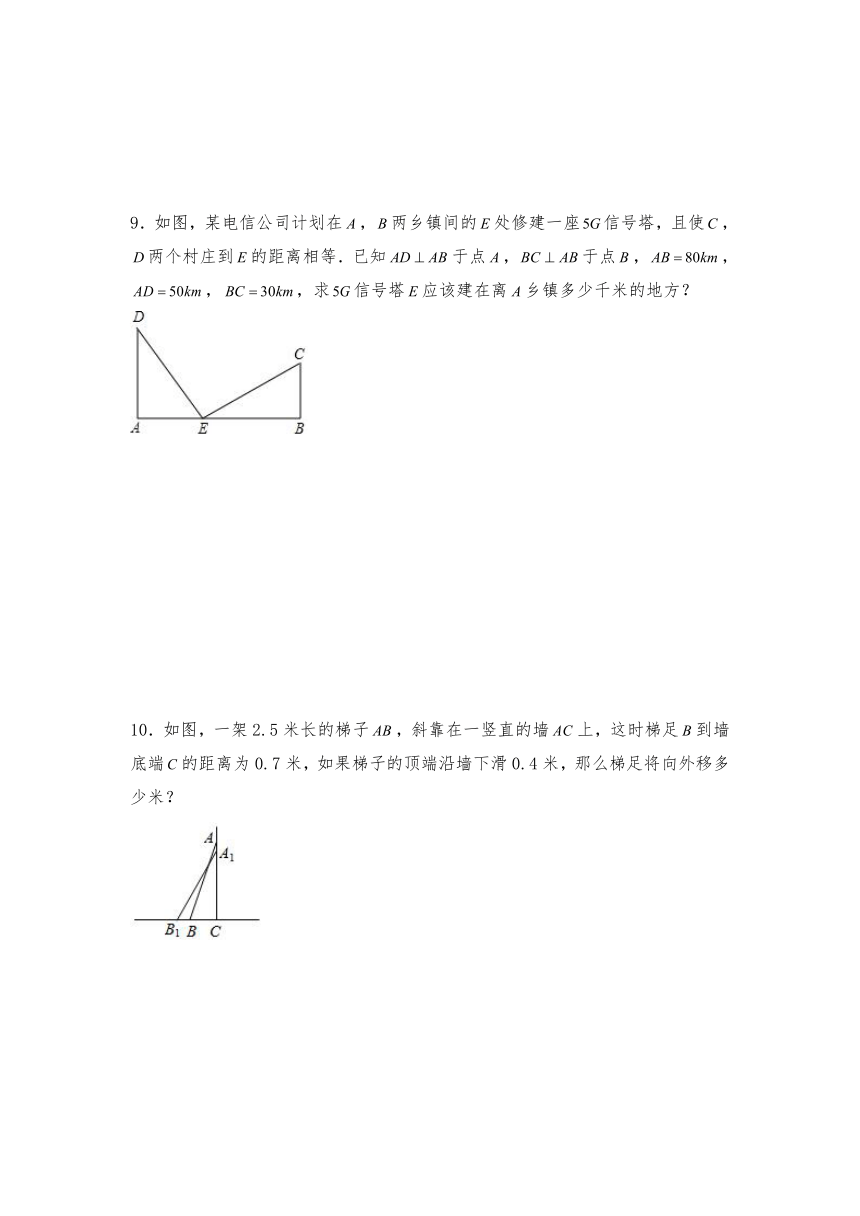
9.如图,某电信公司计划在,两乡镇间的处修建一座信号塔,且使,两个村庄到的距离相等.已知于点,于点,,,,求信号塔应该建在离乡镇多少千米的地方?
10.如图,一架2.5米长的梯子,斜靠在一竖直的墙上,这时梯足到墙底端的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?
11.笔直的河流一侧有一旅游地,河边有两个漂流点,.其中,由于某种原因,由到的路现在已经不通,为方便游客决定在河边新建一个漂流点,,在同一直线上),并新修一条路,测得千米,千米,千米.
(1)判断的形状,并说明理由;
(2)求原路线的长.
12.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪处的正前方的处,过了后,测得小汽车与车速检测仪间距离为,这辆小汽车超速了吗?(参考数据转换:
13.(1)求满足的未知数的值.
(2)如图,为修铁路需要通隧道,测得,,,若每天凿,则需要几天才能把隧道凿通?
14.在甲村至乙村的公路旁有一块山地正在开发,现有一处需要爆破.已知点与公路上的停靠站的距离为500米,与公路上另一停靠站的距离为1200米,且,如图,为了安全起见,爆破点周围半径400米范围内不得进入,问在进行爆破时,公路段是否有危险,是否需要暂时封锁?请通过计算进行说明.
15.如图所示的一块草坪,已知,,,,,求这块草坪的面积.
16.如图所示,一架梯子斜靠在墙面上,且的长为2.5米.
(1)若梯子底端离墙角的距离为1.5米,求这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑0.5米到点,那么梯子的底端在水平方向滑动的距离为多少米?
17.如图,学校操场边上一块空地(阴影部分)需要绿化,连接,测出,,,,,求需要绿化部分的面积.
18.如图,在甲村到乙村的公路旁有一块山地正在开发,现有处需要爆破.已知点与公路上的停靠站、的距离分别为和,且,为了安全起见,如果爆破点周围半径的区域内不能有车辆和行人,问在进行爆破时,公路段是否需要暂时封闭,为什么?
19.一架云梯长,如图那样斜靠在一面墙上,云梯顶端离地面.
(1)这架云梯的底端距墙角有多远?
(2)如果云梯的顶端下滑了,那么它的底部在水平方向滑动了多少?
20.如图,某斜拉桥的主梁垂直于桥面与点,主梁上有两根拉索分别为、.
(1)若拉索,、的长度分别为10米、26米,则拉索 米;
(2)若、的长分别为13米,20米,且固定点、之间的距离为21米,求主梁的高度.
21.如图是俱乐部新打造的一款儿童游戏项目,工作人员告诉小敏,该项目段和段均由不锈钢管材打造,总长度为26米,长方形和长方形均为木质平台的横截面,点在上,点在上,点在上,经过现场测量得知:米,米.
(1)小敏猜想立柱段的长为10米,请判断小敏的猜想是否正确?如果正确,请写出理由,如果错误,请求出立柱段的正确长度;
(2)为加强游戏安全性,俱乐部打算再焊接一段钢索,经测量米,请你求出要焊接的钢索的长.(结果不必化简成最简二次根式)
22.某中学初二年级游同学在学习了勾股定理后对《九章算术》勾股章产生了学习兴趣.今天,他学到了勾股章第7题:
“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”本题大意是:如图,木柱,绳索比木柱长三尺,的长度为8尺,求:绳索的长度.
23.如图,一个直径为的杯子,在它的正中间竖直放一根小木棍,小木棍露出杯子外,当小木棍倒向杯壁时(小木棍底端不动),小木棍顶端正好触到杯口,求小木棍长度.
24.如图,一个直径为(即的圆柱形杯子,在杯子底面的正中间点处竖直放一根筷子,筷子露出杯子外(即,当筷子倒向杯壁时(筷子底端不动),筷子顶端正好触到杯,求筷子的长度.
答案
一、解答题
1.(1)证明:,米,米,
(米,
米,米,
,
;
(2)解:图中阴影部分土地的面积(平方米).
2.解:(1)城受到这次台风的影响,
理由:由点向作垂线,垂足为,
在中,,,则,
因为,所以城要受台风影响;
(2)设上点,千米,则还有一点,有
千米.
因为,所以是等腰三角形,
因为,所以是的垂直平分线,,
在中,千米,千米,
由勾股定理得,(千米),
则千米,
遭受台风影响的时间是:(小时),
答:城遭受这次台风影响时间为4小时.
3.解:过点作,垂足为,
由题意可知:米,米,米;
在中,根据勾股定理,得,
即,,,
(米,
(米;
答:发生火灾的住户窗口距离地面15米.
4.解:连接,
在中,,
在中,,,
而,
即,
,
,
故(元,
答:需要投入3600元经费.
5.解:在中,,
,
,,
设,则,
,
解得:,
答:的长为.
6.解:设,则,
由图可得,,,
中,,
即,
解得,
答:风筝距离地面的高度为12米.
7.解:(1)是直角三角形,
由勾股定理,得.
米,米,
.
,
米.
即,两点间的距离是36米.
(2)过点作于点.
因为,
所以.
所以(米,
即点到直线的距离是28.8米.
8.解:设尺,
尺,尺,
(尺,尺,
在中,尺,尺,尺,
根据勾股定理得:,
整理得:,
即,
解得:,
则秋千绳索的长度为14.5尺.
9.解:设,则,
,,
和都是直角三角形,
,,
又,,,
,
解得.
答:信号塔应该建在离乡镇30千米的地方.
10.解;在直角中,已知,,
则,
,
在直角△中,,且为斜边,
,
答:梯足向外移动了.
11.解:(1)是直角三角形,
理由是:在中,
,
,
,
是直角三角形且;
(2)设千米,则千米,
在中,由已知得,,,
由勾股定理得:,
解这个方程,得,
答:原来的路线的长为千米.
12.解:在中,,;
根据勾股定理可得:
小汽车的速度为;
;
这辆小汽车超速行驶.
答:这辆小汽车超速了.
13.解:(1),
;
(2)因为,
所以.
又因为在中,,
所以
需要的时间:(天,
14.解:公路不需要暂时封锁.
理由如下:如图,过作于.
,
,
因为米,米,
所以,根据勾股定理有(米.
因为
所以(米.
由于400米米,故没有危险,
因此段公路不需要暂时封锁.
15.解:连接,则在中,
,
,
在中,,
,
,
,
.
答:这块地的面积是216平方米.
16.解:(1)根据勾股定理:
所以梯子距离地面的高度为:米;
(2)梯子下滑了0.5米即梯子距离地面的高度为米,
根据勾股定理:米,
所以当梯子的顶端下滑0.5米时,梯子的底端水平后移了米,
答:当梯子的顶端下滑0.5米时,梯子的底端水平后移了0.5米.
17.解:,
在中,,,
由勾股定理得,
在中,,,
,
,
需要绿化部分的面积,
答:需要绿化部分的面积为24.
18.解:如图,过点作于点.
在中,由勾股定理,得:,
所以,
由,
得,
解得,
因为,所以爆破公路段有危险,需要暂时封锁.
19.解:(1)在中,由勾股定理得,
即,
,
答:这架云梯的底端距墙角有7 远;
(2)云梯的顶端下滑了至点,
,
在△中,由勾股定理得,
即,
,
,
答:梯子的底端在水平方向也滑动了.
20.解:(1),、的长度分别为10米、26米,
(米,
(2),
,
,
,
,
,
(米.
21.解:(1)不正确,理由如下:
由题意得:米,米,
设米,则米,
在中,由勾股定理得:,
即,
解得:,
米,
(米,
小敏的猜想不正确,立柱段的正确长度长为9米.
(2)由题意得:米,
(米,
在中,由勾股定理得:(米.
22.解:设尺,则尺,
,
是直角三角形,
由勾股定理得:,
即,
解得:(尺,
答:绳索的长度是尺.
23.解:设杯子的高度是,那么小木棍的高度是,
杯子的直径为,
杯子半径为,
,
即,
解得:,
.
答:小木棍长.
24.解:设筷子的长度是,那么杯子的高度是,
杯子的直径为,
杯子半径为,
,
即,
解得:,
答:筷子的长度是
一、解答题
1.如图,把一块直角三角形土地划出一个三角形后,测得米,米,米,米.
(1)求证:;
(2)求图中阴影部分土地的面积.
2.如图,城气象台测得台风中心在城正西方向的处,以每小时的速度向北偏东的方向移动,距台风中心的范围内是受台风影响的区域.
(1)城是否受到这次台风的影响?为什么?
(2)若城受到这次台风的影响,那么城遭受这次台风影响有多长时间?
3.如图,一高层住宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面3米,问:发生火灾的住户窗口距离地面有多高?
4.已知有一块四边形的空地,如图所示,现计划在空地上种植草皮,经测量,,,,,若每平方米草皮需要100元,求需要投入多少元经费?
5.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根四尺,问折者高几何?”翻译成数学问题是:如图所示,中,,,,求的长.
6.如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度.于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(如图为示意图).请你帮小旭求出风筝距离地面的高度.
7.如图,湖的两岸有,两点,在与成直角的方向上的点处测得米,米.
(1)求,两点间的距离;
(2)求点到直线的距离.
8.如图,秋千静止的时候,踏板离地高一尺尺),将它往前推进两步尺),此时踏板升高离地五尺尺),求秋千绳索或的长度.
9.如图,某电信公司计划在,两乡镇间的处修建一座信号塔,且使,两个村庄到的距离相等.已知于点,于点,,,,求信号塔应该建在离乡镇多少千米的地方?
10.如图,一架2.5米长的梯子,斜靠在一竖直的墙上,这时梯足到墙底端的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?
11.笔直的河流一侧有一旅游地,河边有两个漂流点,.其中,由于某种原因,由到的路现在已经不通,为方便游客决定在河边新建一个漂流点,,在同一直线上),并新修一条路,测得千米,千米,千米.
(1)判断的形状,并说明理由;
(2)求原路线的长.
12.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪处的正前方的处,过了后,测得小汽车与车速检测仪间距离为,这辆小汽车超速了吗?(参考数据转换:
13.(1)求满足的未知数的值.
(2)如图,为修铁路需要通隧道,测得,,,若每天凿,则需要几天才能把隧道凿通?
14.在甲村至乙村的公路旁有一块山地正在开发,现有一处需要爆破.已知点与公路上的停靠站的距离为500米,与公路上另一停靠站的距离为1200米,且,如图,为了安全起见,爆破点周围半径400米范围内不得进入,问在进行爆破时,公路段是否有危险,是否需要暂时封锁?请通过计算进行说明.
15.如图所示的一块草坪,已知,,,,,求这块草坪的面积.
16.如图所示,一架梯子斜靠在墙面上,且的长为2.5米.
(1)若梯子底端离墙角的距离为1.5米,求这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑0.5米到点,那么梯子的底端在水平方向滑动的距离为多少米?
17.如图,学校操场边上一块空地(阴影部分)需要绿化,连接,测出,,,,,求需要绿化部分的面积.
18.如图,在甲村到乙村的公路旁有一块山地正在开发,现有处需要爆破.已知点与公路上的停靠站、的距离分别为和,且,为了安全起见,如果爆破点周围半径的区域内不能有车辆和行人,问在进行爆破时,公路段是否需要暂时封闭,为什么?
19.一架云梯长,如图那样斜靠在一面墙上,云梯顶端离地面.
(1)这架云梯的底端距墙角有多远?
(2)如果云梯的顶端下滑了,那么它的底部在水平方向滑动了多少?
20.如图,某斜拉桥的主梁垂直于桥面与点,主梁上有两根拉索分别为、.
(1)若拉索,、的长度分别为10米、26米,则拉索 米;
(2)若、的长分别为13米,20米,且固定点、之间的距离为21米,求主梁的高度.
21.如图是俱乐部新打造的一款儿童游戏项目,工作人员告诉小敏,该项目段和段均由不锈钢管材打造,总长度为26米,长方形和长方形均为木质平台的横截面,点在上,点在上,点在上,经过现场测量得知:米,米.
(1)小敏猜想立柱段的长为10米,请判断小敏的猜想是否正确?如果正确,请写出理由,如果错误,请求出立柱段的正确长度;
(2)为加强游戏安全性,俱乐部打算再焊接一段钢索,经测量米,请你求出要焊接的钢索的长.(结果不必化简成最简二次根式)
22.某中学初二年级游同学在学习了勾股定理后对《九章算术》勾股章产生了学习兴趣.今天,他学到了勾股章第7题:
“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”本题大意是:如图,木柱,绳索比木柱长三尺,的长度为8尺,求:绳索的长度.
23.如图,一个直径为的杯子,在它的正中间竖直放一根小木棍,小木棍露出杯子外,当小木棍倒向杯壁时(小木棍底端不动),小木棍顶端正好触到杯口,求小木棍长度.
24.如图,一个直径为(即的圆柱形杯子,在杯子底面的正中间点处竖直放一根筷子,筷子露出杯子外(即,当筷子倒向杯壁时(筷子底端不动),筷子顶端正好触到杯,求筷子的长度.
答案
一、解答题
1.(1)证明:,米,米,
(米,
米,米,
,
;
(2)解:图中阴影部分土地的面积(平方米).
2.解:(1)城受到这次台风的影响,
理由:由点向作垂线,垂足为,
在中,,,则,
因为,所以城要受台风影响;
(2)设上点,千米,则还有一点,有
千米.
因为,所以是等腰三角形,
因为,所以是的垂直平分线,,
在中,千米,千米,
由勾股定理得,(千米),
则千米,
遭受台风影响的时间是:(小时),
答:城遭受这次台风影响时间为4小时.
3.解:过点作,垂足为,
由题意可知:米,米,米;
在中,根据勾股定理,得,
即,,,
(米,
(米;
答:发生火灾的住户窗口距离地面15米.
4.解:连接,
在中,,
在中,,,
而,
即,
,
,
故(元,
答:需要投入3600元经费.
5.解:在中,,
,
,,
设,则,
,
解得:,
答:的长为.
6.解:设,则,
由图可得,,,
中,,
即,
解得,
答:风筝距离地面的高度为12米.
7.解:(1)是直角三角形,
由勾股定理,得.
米,米,
.
,
米.
即,两点间的距离是36米.
(2)过点作于点.
因为,
所以.
所以(米,
即点到直线的距离是28.8米.
8.解:设尺,
尺,尺,
(尺,尺,
在中,尺,尺,尺,
根据勾股定理得:,
整理得:,
即,
解得:,
则秋千绳索的长度为14.5尺.
9.解:设,则,
,,
和都是直角三角形,
,,
又,,,
,
解得.
答:信号塔应该建在离乡镇30千米的地方.
10.解;在直角中,已知,,
则,
,
在直角△中,,且为斜边,
,
答:梯足向外移动了.
11.解:(1)是直角三角形,
理由是:在中,
,
,
,
是直角三角形且;
(2)设千米,则千米,
在中,由已知得,,,
由勾股定理得:,
解这个方程,得,
答:原来的路线的长为千米.
12.解:在中,,;
根据勾股定理可得:
小汽车的速度为;
;
这辆小汽车超速行驶.
答:这辆小汽车超速了.
13.解:(1),
;
(2)因为,
所以.
又因为在中,,
所以
需要的时间:(天,
14.解:公路不需要暂时封锁.
理由如下:如图,过作于.
,
,
因为米,米,
所以,根据勾股定理有(米.
因为
所以(米.
由于400米米,故没有危险,
因此段公路不需要暂时封锁.
15.解:连接,则在中,
,
,
在中,,
,
,
,
.
答:这块地的面积是216平方米.
16.解:(1)根据勾股定理:
所以梯子距离地面的高度为:米;
(2)梯子下滑了0.5米即梯子距离地面的高度为米,
根据勾股定理:米,
所以当梯子的顶端下滑0.5米时,梯子的底端水平后移了米,
答:当梯子的顶端下滑0.5米时,梯子的底端水平后移了0.5米.
17.解:,
在中,,,
由勾股定理得,
在中,,,
,
,
需要绿化部分的面积,
答:需要绿化部分的面积为24.
18.解:如图,过点作于点.
在中,由勾股定理,得:,
所以,
由,
得,
解得,
因为,所以爆破公路段有危险,需要暂时封锁.
19.解:(1)在中,由勾股定理得,
即,
,
答:这架云梯的底端距墙角有7 远;
(2)云梯的顶端下滑了至点,
,
在△中,由勾股定理得,
即,
,
,
答:梯子的底端在水平方向也滑动了.
20.解:(1),、的长度分别为10米、26米,
(米,
(2),
,
,
,
,
,
(米.
21.解:(1)不正确,理由如下:
由题意得:米,米,
设米,则米,
在中,由勾股定理得:,
即,
解得:,
米,
(米,
小敏的猜想不正确,立柱段的正确长度长为9米.
(2)由题意得:米,
(米,
在中,由勾股定理得:(米.
22.解:设尺,则尺,
,
是直角三角形,
由勾股定理得:,
即,
解得:(尺,
答:绳索的长度是尺.
23.解:设杯子的高度是,那么小木棍的高度是,
杯子的直径为,
杯子半径为,
,
即,
解得:,
.
答:小木棍长.
24.解:设筷子的长度是,那么杯子的高度是,
杯子的直径为,
杯子半径为,
,
即,
解得:,
答:筷子的长度是
