沪科版八年级数学下册试题 勾股定理与最短路径问题(含答案)
文档属性
| 名称 | 沪科版八年级数学下册试题 勾股定理与最短路径问题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 701.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-08 00:00:00 | ||
图片预览

文档简介
勾股定理与最短路径问题
一、选择题
1.如图所示的圆柱体中底面圆的半径是,高为3,若一只小虫从点出发沿着圆柱体的侧面爬行到点,则小虫爬行的最短路程是
A.5 B. C. D.4
2.如图,台阶阶梯每一层高,宽,长,一只蚂蚁从点爬到点,最短路程是
A. B. C.120 D.130
3.如图,圆柱的高为,底面半径为,在圆柱下底面的点处有一只蚂蚁,它想吃到上底面处的食物,已知四边形的边、恰好是上、下底面的直径、问:蚂蚁食到食物爬行的最短距离是 .
A.5 B. C. D.
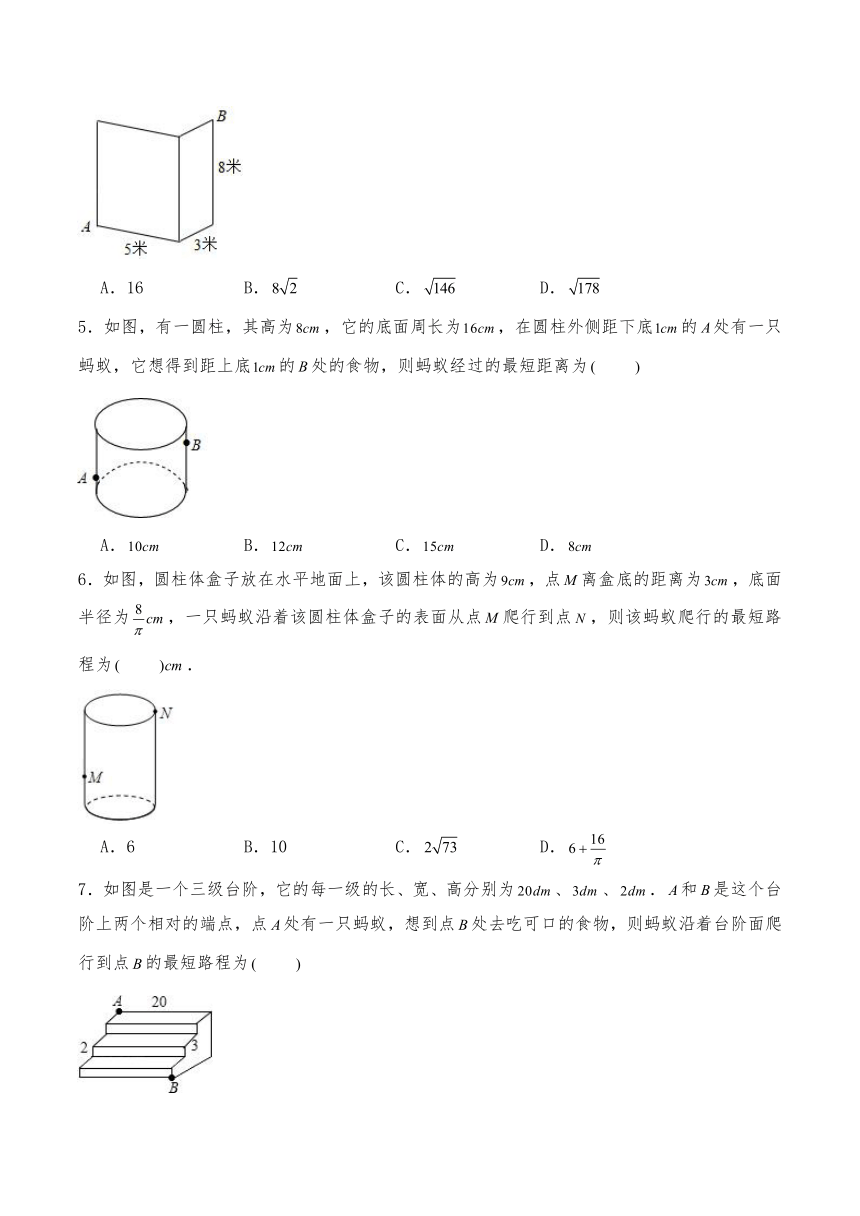
4.小南同学报名参加了南开中学的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示,他根据学过的数学知识准确地判断出:从点攀爬到点的最短路径为 米.
A.16 B. C. D.
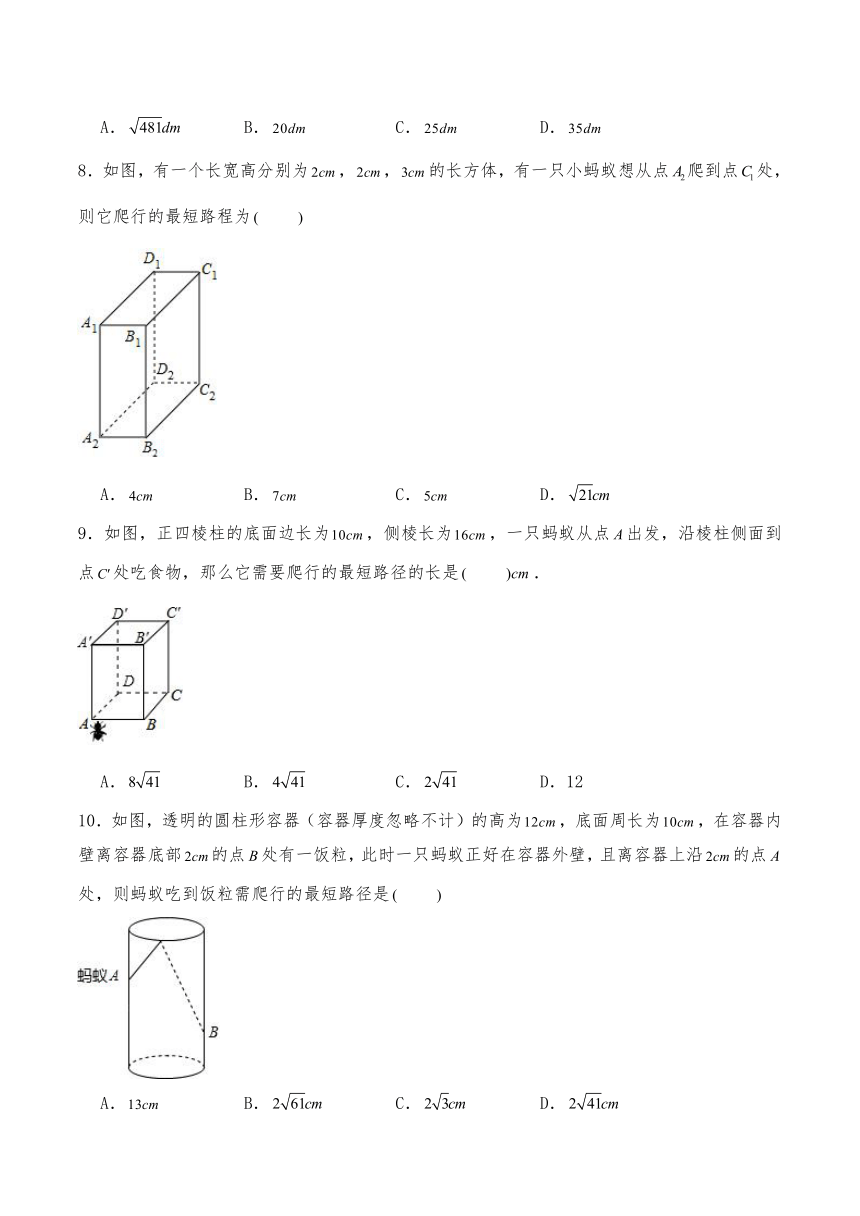
5.如图,有一圆柱,其高为,它的底面周长为,在圆柱外侧距下底的处有一只蚂蚁,它想得到距上底的处的食物,则蚂蚁经过的最短距离为
A. B. C. D.
6.如图,圆柱体盒子放在水平地面上,该圆柱体的高为,点离盒底的距离为,底面半径为,一只蚂蚁沿着该圆柱体盒子的表面从点爬行到点,则该蚂蚁爬行的最短路程为 .
A.6 B.10 C. D.
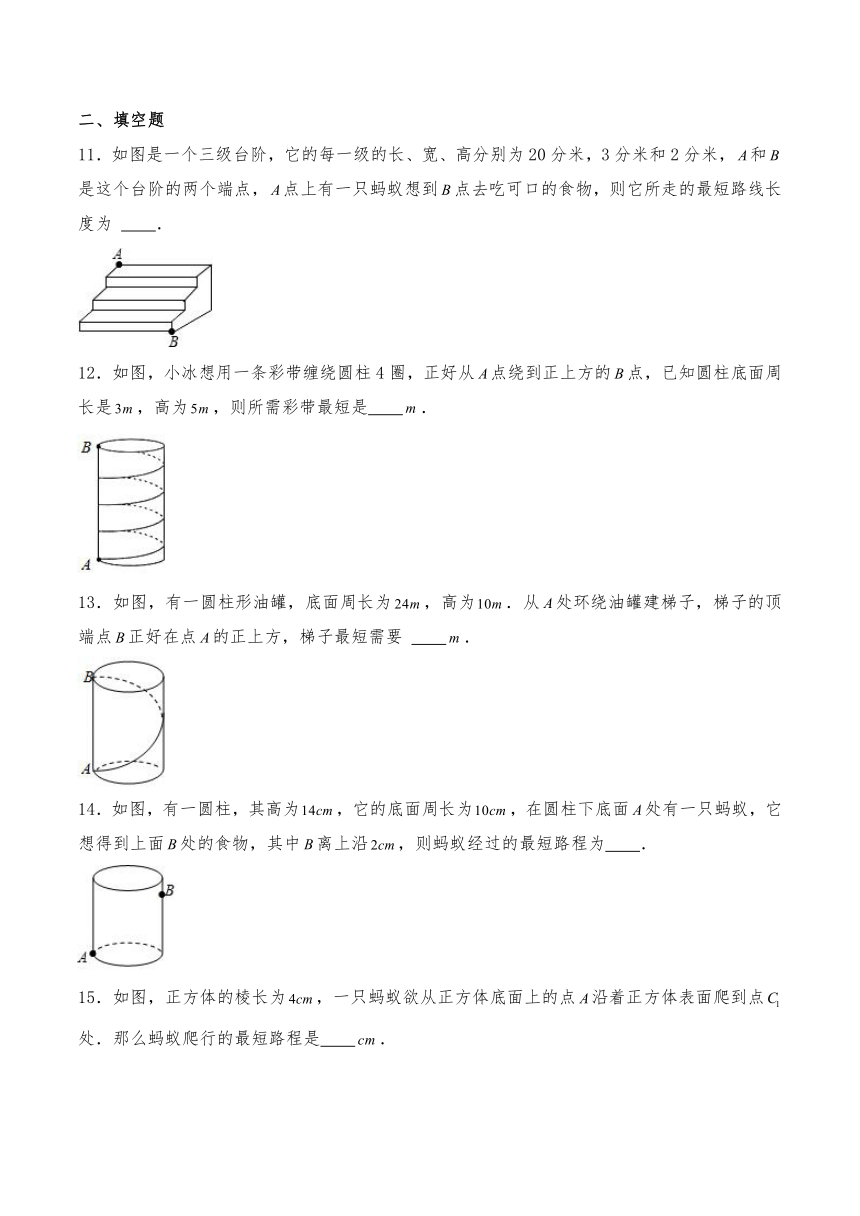
7.如图是一个三级台阶,它的每一级的长、宽、高分别为、、.和是这个台阶上两个相对的端点,点处有一只蚂蚁,想到点处去吃可口的食物,则蚂蚁沿着台阶面爬行到点的最短路程为
A. B. C. D.
8.如图,有一个长宽高分别为,,的长方体,有一只小蚂蚁想从点爬到点处,则它爬行的最短路程为
A. B. C. D.
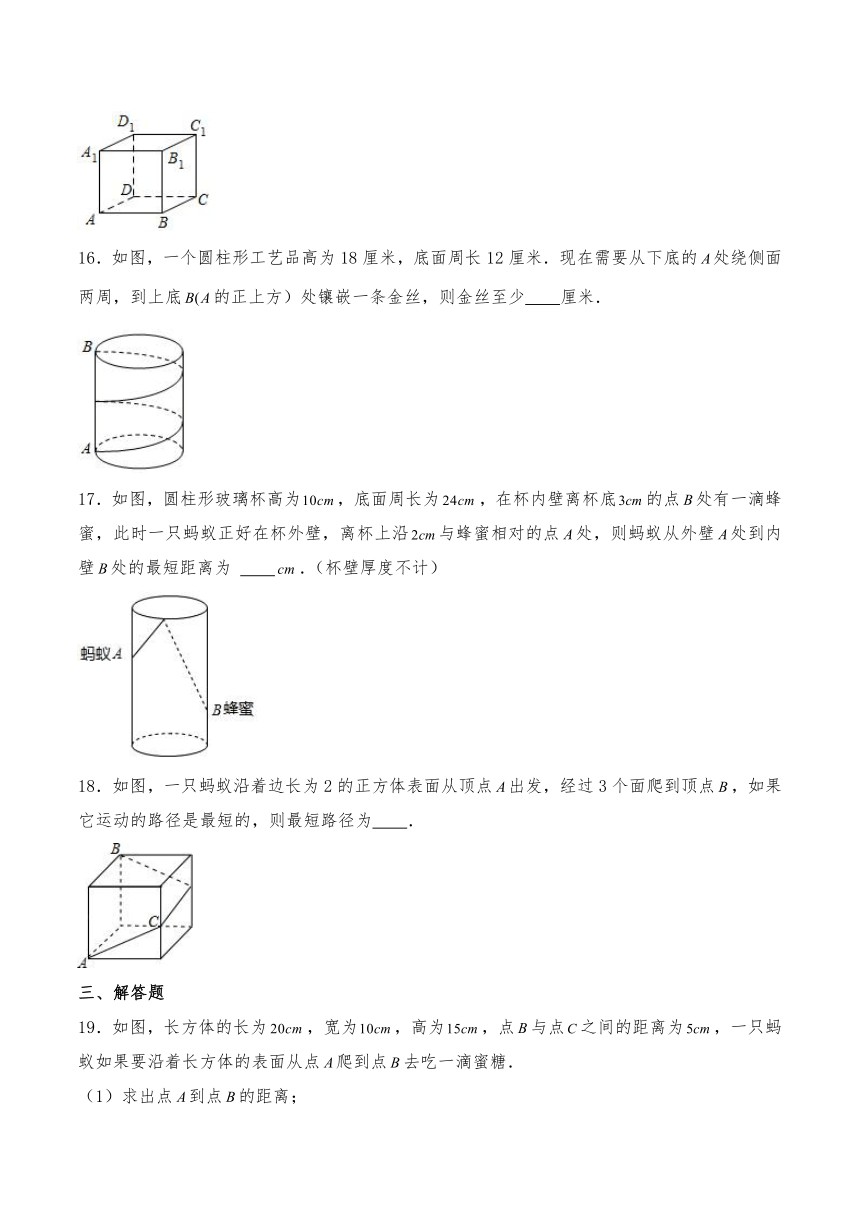
9.如图,正四棱柱的底面边长为,侧棱长为,一只蚂蚁从点出发,沿棱柱侧面到点处吃食物,那么它需要爬行的最短路径的长是 .
A. B. C. D.12
10.如图,透明的圆柱形容器(容器厚度忽略不计)的高为,底面周长为,在容器内壁离容器底部的点处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿的点处,则蚂蚁吃到饭粒需爬行的最短路径是
A. B. C. D.
二、填空题
11.如图是一个三级台阶,它的每一级的长、宽、高分别为20分米,3分米和2分米,和是这个台阶的两个端点,点上有一只蚂蚁想到点去吃可口的食物,则它所走的最短路线长度为 .
12.如图,小冰想用一条彩带缠绕圆柱4圈,正好从点绕到正上方的点,已知圆柱底面周长是,高为,则所需彩带最短是 .
13.如图,有一圆柱形油罐,底面周长为,高为.从处环绕油罐建梯子,梯子的顶端点正好在点的正上方,梯子最短需要 .
14.如图,有一圆柱,其高为,它的底面周长为,在圆柱下底面处有一只蚂蚁,它想得到上面处的食物,其中离上沿,则蚂蚁经过的最短路程为 .
15.如图,正方体的棱长为,一只蚂蚁欲从正方体底面上的点沿着正方体表面爬到点处.那么蚂蚁爬行的最短路程是 .
16.如图,一个圆柱形工艺品高为18厘米,底面周长12厘米.现在需要从下底的处绕侧面两周,到上底的正上方)处镶嵌一条金丝,则金丝至少 厘米.
17.如图,圆柱形玻璃杯高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处的最短距离为 .(杯壁厚度不计)
18.如图,一只蚂蚁沿着边长为2的正方体表面从顶点出发,经过3个面爬到顶点,如果它运动的路径是最短的,则最短路径为 .
三、解答题
19.如图,长方体的长为,宽为,高为,点与点之间的距离为,一只蚂蚁如果要沿着长方体的表面从点爬到点去吃一滴蜜糖.
(1)求出点到点的距离;
(2)求蚂蚁从点爬到点的最短路程是多少?
20.如图,(1)一只蚂蚁要从长方体的一个顶点沿表面爬行到顶点,怎样爬行路线最短?为什么?
(2)若长方体的长为3、宽为1、高为2,蚂蚁要沿长方体的表面,从顶点走到顶点,试画出不重复情况的展开示意图,并通过计算比较求出最短距离.
21.如图,一只蚂蚁从长为、宽为,高是的长方体纸箱的点沿纸箱爬到点,那么它所走的最短路线的长是多少?
22.在科幻世界里有各种造型奇特的小山.如图1是一座三棱锥小山,侧面展开图如图2所示,每个侧面完全相同.一只小狐狸在半山腰点处想饱览四周风景,它沿路径“”绕小山一周最终以最短路径到达山脚处,当小狐狸沿侧面的路径运动时,若,则称这段路为“上坡路”;若,则称这段路为“下坡路”;若,则称这段路为“上坡路”;若,则称这段路为“下坡路”.当时,在图2中画出从点沿侧面环绕一周到达山脚点处的最短路径,并判断在侧面、侧面上走的是上坡路还是下坡路?
23.如图,已知圆柱底面的直径,圆柱的高,在圆柱的侧面上,过点,嵌有一圈长度最短的金属丝.
(1)现将圆柱侧面沿剪开,所得的圆柱侧面展开图是 .
(2)求该长度最短的金属丝的长.
24.如图1,一只蚂蚁要从边长为正方体的一个顶点沿表面爬行到顶点,怎样爬行路线最短?如果要爬行到顶点呢?请完成下列问题:
(1)图2是将立方体表面展开的一部分,请将正方体的表面展开图补充完整;(画一种即可)
(2)在图2中画出点到点的最短爬行路线,最短路径为: ;
(3)在图2中标出点,并画出、两点的最短爬行路线(画一种即可),最短路径为 .
答案
一、选择题
..........
二、填空题
11.25分米. 12.13. 13.26. 14..
15.. 16.30. 17.15. 18..
三、解答题
19.(1),
答:点到点的距离为;
(2)把上面展开到左侧上,连接,
如图1,
根据勾股定理得:;
把右侧面展开到正面上,连接,如图2,
根据勾股定理得:,
则需要爬行的最短距离是.
把向上的面展开到正面上,连接,如图3,
根据勾股定理得:,
综上所述,从点爬到点的距离为:,,;
,
则需要爬行的最短距离是.
20.(1)连接,蚂蚁沿着爬行路线最短;
理由:两点之间线段最短;
(2)因为平面展开图不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.
①展开前面右面由勾股定理得;
②展开前面上面由勾股定理得;
③展开左面上面由勾股定理得.
所以最短路径的长为.
21.由题意可得,
当展开前面和右面时,最短路线长是:;
当展开前面和上面时,最短路线长是:;
当展开左面和上面时,最短路线长是:;
,
一只蚂蚁从长为、宽为,高是的长方体纸箱的点沿纸箱爬到点,那么它所走的最短路线的长是.
22.如图2,连接交于点,交于点,
线段即为从点沿侧面环绕一周到达山脚点处的最短路径,
则,,
,
,,,
,
,,
,,
,
,
在侧面上走的是上坡路,
,
,
,,
,
,
,
,
在侧面上走的是下坡路,
答:在侧面上走的是上坡路,在侧面上走的是下坡路.
23.(1)因圆柱的侧面展开面为长方形,展开应该是两线段,且有公共点.
故选:;
(2)解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为的长度.
圆柱底面的直径,圆柱的高,
该长度最短的金属丝的长为.
24.(1)如图所示,
(2)如图所示,连接,线段的即为点到点的最短爬行路线,
故答案为:线段;
(3)如图所示,线段即为、两点的最短爬行路线,
故答案为:线段.
一、选择题
1.如图所示的圆柱体中底面圆的半径是,高为3,若一只小虫从点出发沿着圆柱体的侧面爬行到点,则小虫爬行的最短路程是
A.5 B. C. D.4
2.如图,台阶阶梯每一层高,宽,长,一只蚂蚁从点爬到点,最短路程是
A. B. C.120 D.130
3.如图,圆柱的高为,底面半径为,在圆柱下底面的点处有一只蚂蚁,它想吃到上底面处的食物,已知四边形的边、恰好是上、下底面的直径、问:蚂蚁食到食物爬行的最短距离是 .
A.5 B. C. D.
4.小南同学报名参加了南开中学的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示,他根据学过的数学知识准确地判断出:从点攀爬到点的最短路径为 米.
A.16 B. C. D.
5.如图,有一圆柱,其高为,它的底面周长为,在圆柱外侧距下底的处有一只蚂蚁,它想得到距上底的处的食物,则蚂蚁经过的最短距离为
A. B. C. D.
6.如图,圆柱体盒子放在水平地面上,该圆柱体的高为,点离盒底的距离为,底面半径为,一只蚂蚁沿着该圆柱体盒子的表面从点爬行到点,则该蚂蚁爬行的最短路程为 .
A.6 B.10 C. D.
7.如图是一个三级台阶,它的每一级的长、宽、高分别为、、.和是这个台阶上两个相对的端点,点处有一只蚂蚁,想到点处去吃可口的食物,则蚂蚁沿着台阶面爬行到点的最短路程为
A. B. C. D.
8.如图,有一个长宽高分别为,,的长方体,有一只小蚂蚁想从点爬到点处,则它爬行的最短路程为
A. B. C. D.
9.如图,正四棱柱的底面边长为,侧棱长为,一只蚂蚁从点出发,沿棱柱侧面到点处吃食物,那么它需要爬行的最短路径的长是 .
A. B. C. D.12
10.如图,透明的圆柱形容器(容器厚度忽略不计)的高为,底面周长为,在容器内壁离容器底部的点处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿的点处,则蚂蚁吃到饭粒需爬行的最短路径是
A. B. C. D.
二、填空题
11.如图是一个三级台阶,它的每一级的长、宽、高分别为20分米,3分米和2分米,和是这个台阶的两个端点,点上有一只蚂蚁想到点去吃可口的食物,则它所走的最短路线长度为 .
12.如图,小冰想用一条彩带缠绕圆柱4圈,正好从点绕到正上方的点,已知圆柱底面周长是,高为,则所需彩带最短是 .
13.如图,有一圆柱形油罐,底面周长为,高为.从处环绕油罐建梯子,梯子的顶端点正好在点的正上方,梯子最短需要 .
14.如图,有一圆柱,其高为,它的底面周长为,在圆柱下底面处有一只蚂蚁,它想得到上面处的食物,其中离上沿,则蚂蚁经过的最短路程为 .
15.如图,正方体的棱长为,一只蚂蚁欲从正方体底面上的点沿着正方体表面爬到点处.那么蚂蚁爬行的最短路程是 .
16.如图,一个圆柱形工艺品高为18厘米,底面周长12厘米.现在需要从下底的处绕侧面两周,到上底的正上方)处镶嵌一条金丝,则金丝至少 厘米.
17.如图,圆柱形玻璃杯高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处的最短距离为 .(杯壁厚度不计)
18.如图,一只蚂蚁沿着边长为2的正方体表面从顶点出发,经过3个面爬到顶点,如果它运动的路径是最短的,则最短路径为 .
三、解答题
19.如图,长方体的长为,宽为,高为,点与点之间的距离为,一只蚂蚁如果要沿着长方体的表面从点爬到点去吃一滴蜜糖.
(1)求出点到点的距离;
(2)求蚂蚁从点爬到点的最短路程是多少?
20.如图,(1)一只蚂蚁要从长方体的一个顶点沿表面爬行到顶点,怎样爬行路线最短?为什么?
(2)若长方体的长为3、宽为1、高为2,蚂蚁要沿长方体的表面,从顶点走到顶点,试画出不重复情况的展开示意图,并通过计算比较求出最短距离.
21.如图,一只蚂蚁从长为、宽为,高是的长方体纸箱的点沿纸箱爬到点,那么它所走的最短路线的长是多少?
22.在科幻世界里有各种造型奇特的小山.如图1是一座三棱锥小山,侧面展开图如图2所示,每个侧面完全相同.一只小狐狸在半山腰点处想饱览四周风景,它沿路径“”绕小山一周最终以最短路径到达山脚处,当小狐狸沿侧面的路径运动时,若,则称这段路为“上坡路”;若,则称这段路为“下坡路”;若,则称这段路为“上坡路”;若,则称这段路为“下坡路”.当时,在图2中画出从点沿侧面环绕一周到达山脚点处的最短路径,并判断在侧面、侧面上走的是上坡路还是下坡路?
23.如图,已知圆柱底面的直径,圆柱的高,在圆柱的侧面上,过点,嵌有一圈长度最短的金属丝.
(1)现将圆柱侧面沿剪开,所得的圆柱侧面展开图是 .
(2)求该长度最短的金属丝的长.
24.如图1,一只蚂蚁要从边长为正方体的一个顶点沿表面爬行到顶点,怎样爬行路线最短?如果要爬行到顶点呢?请完成下列问题:
(1)图2是将立方体表面展开的一部分,请将正方体的表面展开图补充完整;(画一种即可)
(2)在图2中画出点到点的最短爬行路线,最短路径为: ;
(3)在图2中标出点,并画出、两点的最短爬行路线(画一种即可),最短路径为 .
答案
一、选择题
..........
二、填空题
11.25分米. 12.13. 13.26. 14..
15.. 16.30. 17.15. 18..
三、解答题
19.(1),
答:点到点的距离为;
(2)把上面展开到左侧上,连接,
如图1,
根据勾股定理得:;
把右侧面展开到正面上,连接,如图2,
根据勾股定理得:,
则需要爬行的最短距离是.
把向上的面展开到正面上,连接,如图3,
根据勾股定理得:,
综上所述,从点爬到点的距离为:,,;
,
则需要爬行的最短距离是.
20.(1)连接,蚂蚁沿着爬行路线最短;
理由:两点之间线段最短;
(2)因为平面展开图不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.
①展开前面右面由勾股定理得;
②展开前面上面由勾股定理得;
③展开左面上面由勾股定理得.
所以最短路径的长为.
21.由题意可得,
当展开前面和右面时,最短路线长是:;
当展开前面和上面时,最短路线长是:;
当展开左面和上面时,最短路线长是:;
,
一只蚂蚁从长为、宽为,高是的长方体纸箱的点沿纸箱爬到点,那么它所走的最短路线的长是.
22.如图2,连接交于点,交于点,
线段即为从点沿侧面环绕一周到达山脚点处的最短路径,
则,,
,
,,,
,
,,
,,
,
,
在侧面上走的是上坡路,
,
,
,,
,
,
,
,
在侧面上走的是下坡路,
答:在侧面上走的是上坡路,在侧面上走的是下坡路.
23.(1)因圆柱的侧面展开面为长方形,展开应该是两线段,且有公共点.
故选:;
(2)解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为的长度.
圆柱底面的直径,圆柱的高,
该长度最短的金属丝的长为.
24.(1)如图所示,
(2)如图所示,连接,线段的即为点到点的最短爬行路线,
故答案为:线段;
(3)如图所示,线段即为、两点的最短爬行路线,
故答案为:线段.
