2023年上海市中考数学考前冲刺试卷(含解析)
文档属性
| 名称 | 2023年上海市中考数学考前冲刺试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 200.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-08 00:00:00 | ||
图片预览

文档简介
上海市2023年中考数学考前冲刺试卷
一、单选题(共6题;共24分)
1.(4分)若单项式 与 的和仍是单项式,则 的值为( )
A.21 B.-21 C.29 D.-29
2.(4分)实数a、b在数轴上的位置如图所示,那么化简|a﹣b|﹣ 的结果是( )
A.2a﹣b B.b C.﹣b D.﹣2a+b
3.(4分)下列调查中,适合用全面调查的是()
A.了解20万只节能灯的使用寿命
B.了解某班35名学生的视力情况
C.了解某条河流的水质情况
D.了解全国居民对“垃圾分类”有关内容的认识程度
4.(4分)若点,在反比例函数的图象上,且,则m的取值范围是( )
A. B.
C. D.或
5.(4分)若两圆的圆心距为3,两圆的半径分别是方程x2-4x+3=0的两个根,则两圆的位置关 系是 ( )
A.相交 B.外离 C.内含 D.外切
6.(4分)下列命题中,是真命题的是( )
A.算术平方根等于自身的数只有1
B. ×|﹣1|×1是最简二次根式
C.只有一个角等于60°的三角形是等边三角形
D.三角形内角和等于180度
二、填空题(共12题;共48分)
7.(4分) 的相反数是 .
8.(4分)分解因式:ab﹣ab2= .
9.(4分)方程=0的根是 .
10.(4分)一枚质地均匀的正方体骰子,六个面分别刻有 到 的点数,小涛同学掷一次骰子,骰子的正面朝上的点数是 的倍数的概率是 .
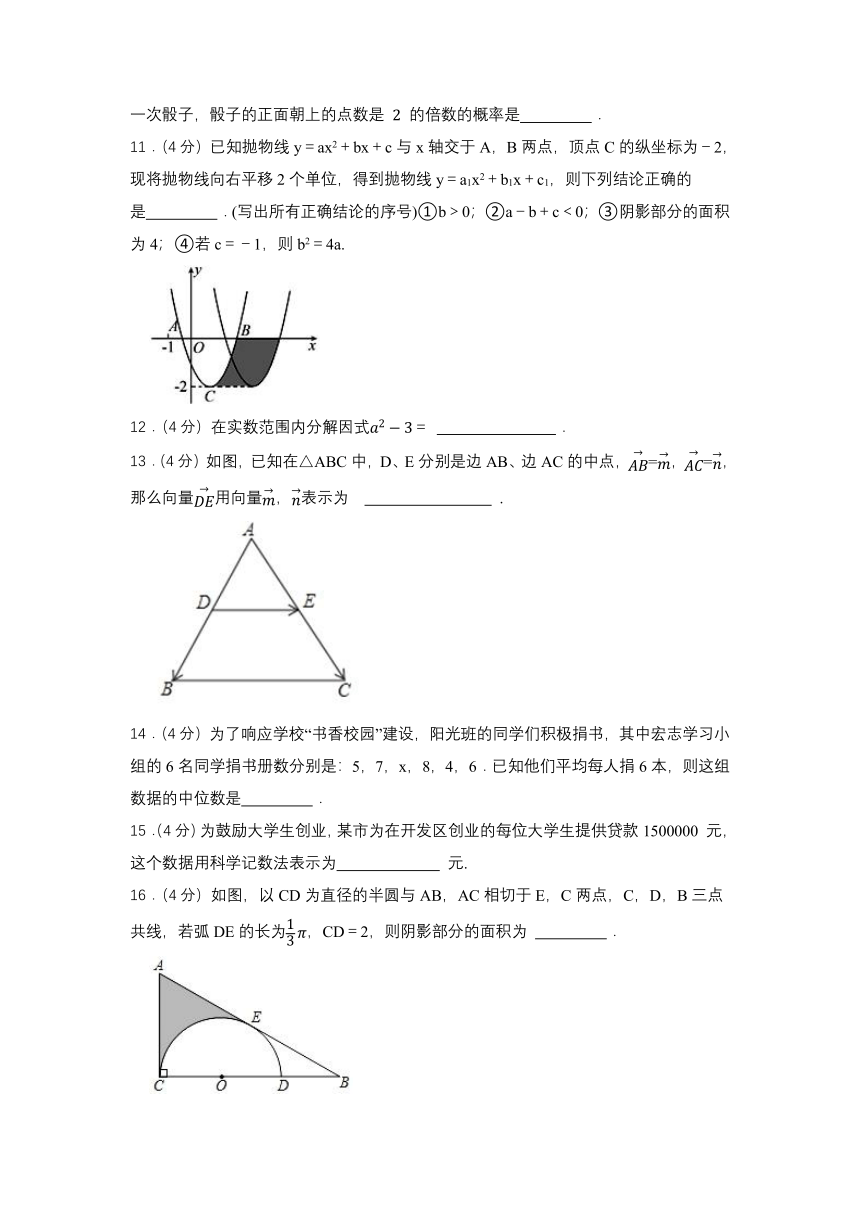
11.(4分)已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是 .(写出所有正确结论的序号)①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
12.(4分)在实数范围内分解因式= .
13.(4分)如图,已知在△ABC中,D、E分别是边AB、边AC的中点,=,=,那么向量用向量,表示为 .
14.(4分)为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的6名同学捐书册数分别是:5,7,x,8,4,6.已知他们平均每人捐6本,则这组数据的中位数是 .
15.(4分)为鼓励大学生创业,某市为在开发区创业的每位大学生提供贷款1500000 元,这个数据用科学记数法表示为 元.
16.(4分)如图,以CD为直径的半圆与AB,AC相切于E,C两点,C,D,B三点共线,若弧DE的长为,CD=2,则阴影部分的面积为 .
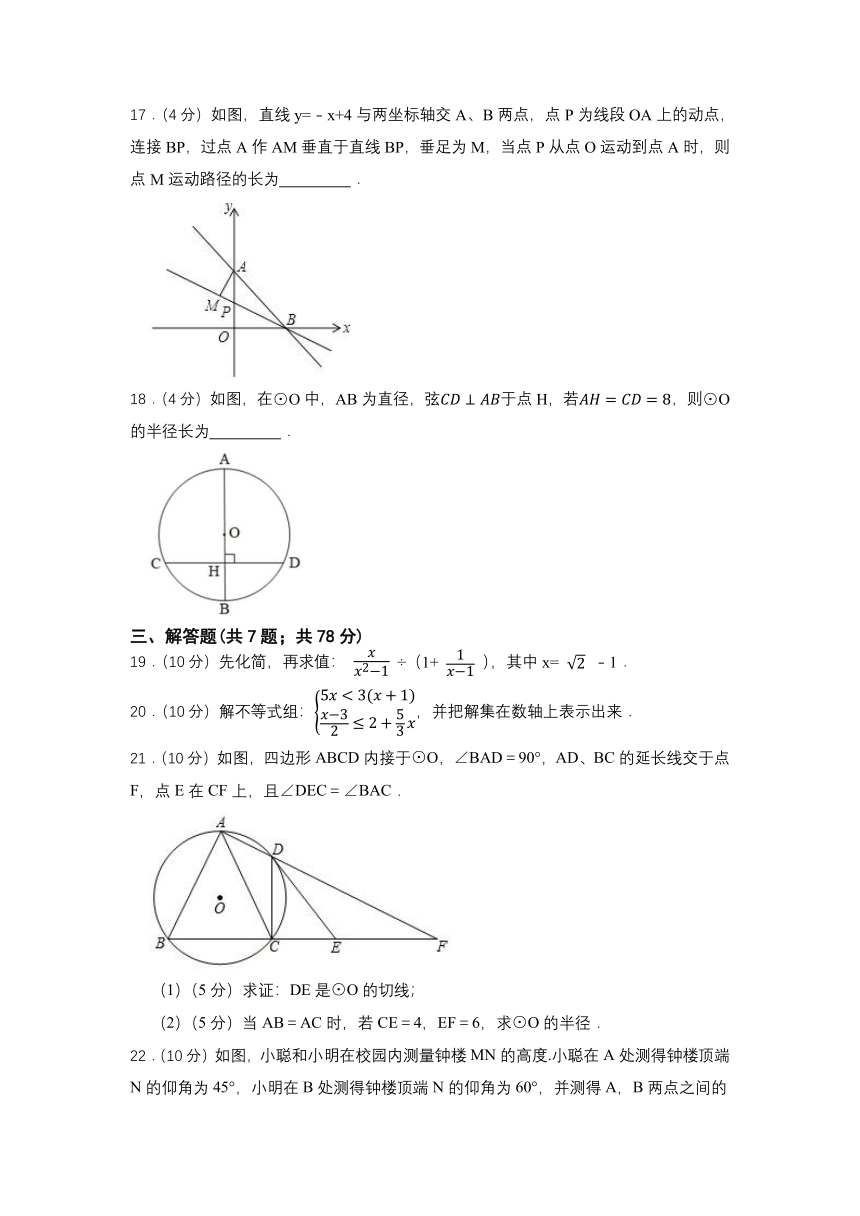
17.(4分)如图,直线y=﹣x+4与两坐标轴交A、B两点,点P为线段OA上的动点,连接BP,过点A作AM垂直于直线BP,垂足为M,当点P从点O运动到点A时,则点M运动路径的长为 .
18.(4分)如图,在⊙O中,AB为直径,弦于点H,若,则⊙O的半径长为 .
三、解答题(共7题;共78分)
19.(10分)先化简,再求值: ÷(1+ ),其中x= ﹣1.
20.(10分)解不等式组:,并把解集在数轴上表示出来.
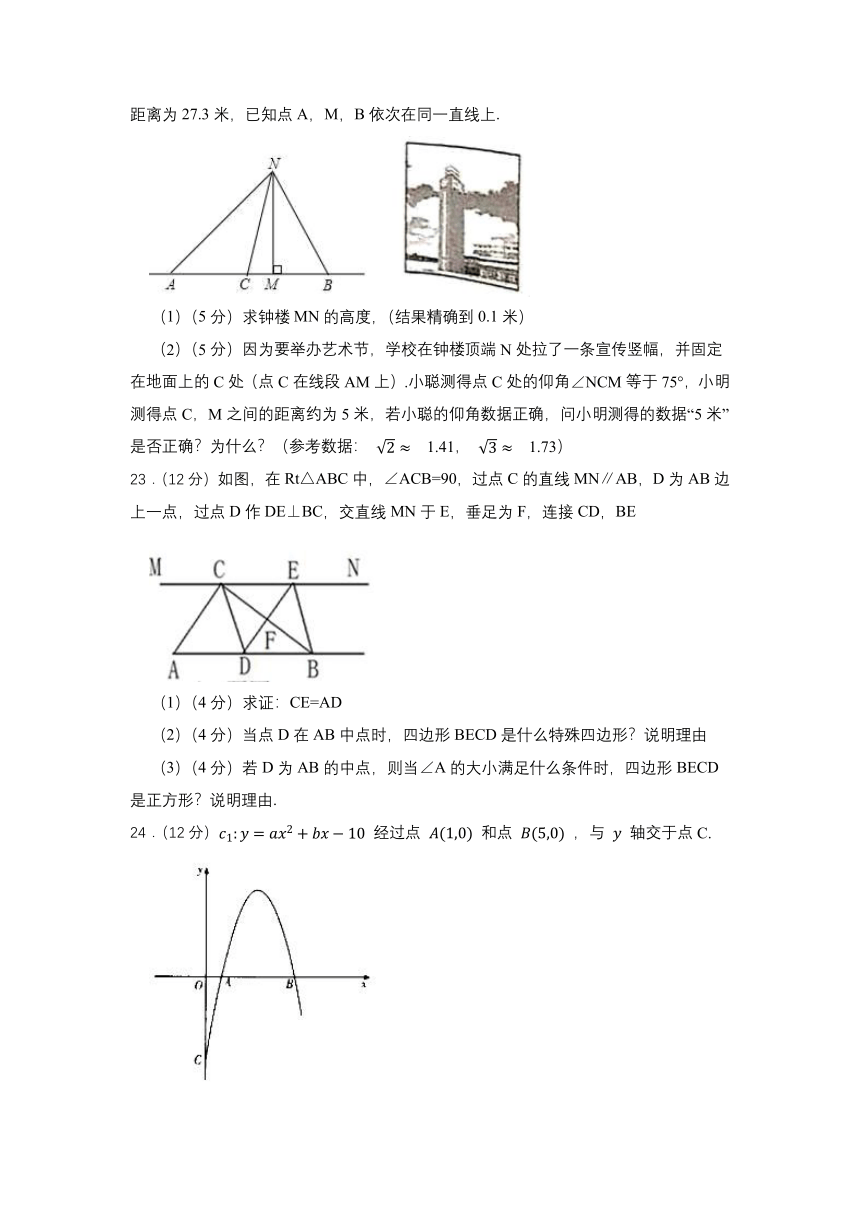
21.(10分)如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)(5分)求证:DE是⊙O的切线;
(2)(5分)当AB=AC时,若CE=4,EF=6,求⊙O的半径.
22.(10分)如图,小聪和小明在校园内测量钟楼MN的高度.小聪在A处测得钟楼顶端N的仰角为45°,小明在B处测得钟楼顶端N的仰角为60°,并测得A,B两点之间的距离为27.3米,已知点A,M,B依次在同一直线上.
(1)(5分)求钟楼MN的高度,(结果精确到0.1米)
(2)(5分)因为要举办艺术节,学校在钟楼顶端N处拉了一条宣传竖幅,并固定在地面上的C处(点C在线段AM上).小聪测得点C处的仰角∠NCM等于75°,小明测得点C,M之间的距离约为5米,若小聪的仰角数据正确,问小明测得的数据“5米”是否正确?为什么?(参考数据: 1.41, 1.73)
23.(12分)如图,在Rt△ABC中,∠ACB=90,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE
(1)(4分)求证:CE=AD
(2)(4分)当点D在AB中点时,四边形BECD是什么特殊四边形?说明理由
(3)(4分)若D为AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?说明理由.
24.(12分) 经过点 和点 ,与 轴交于点C.
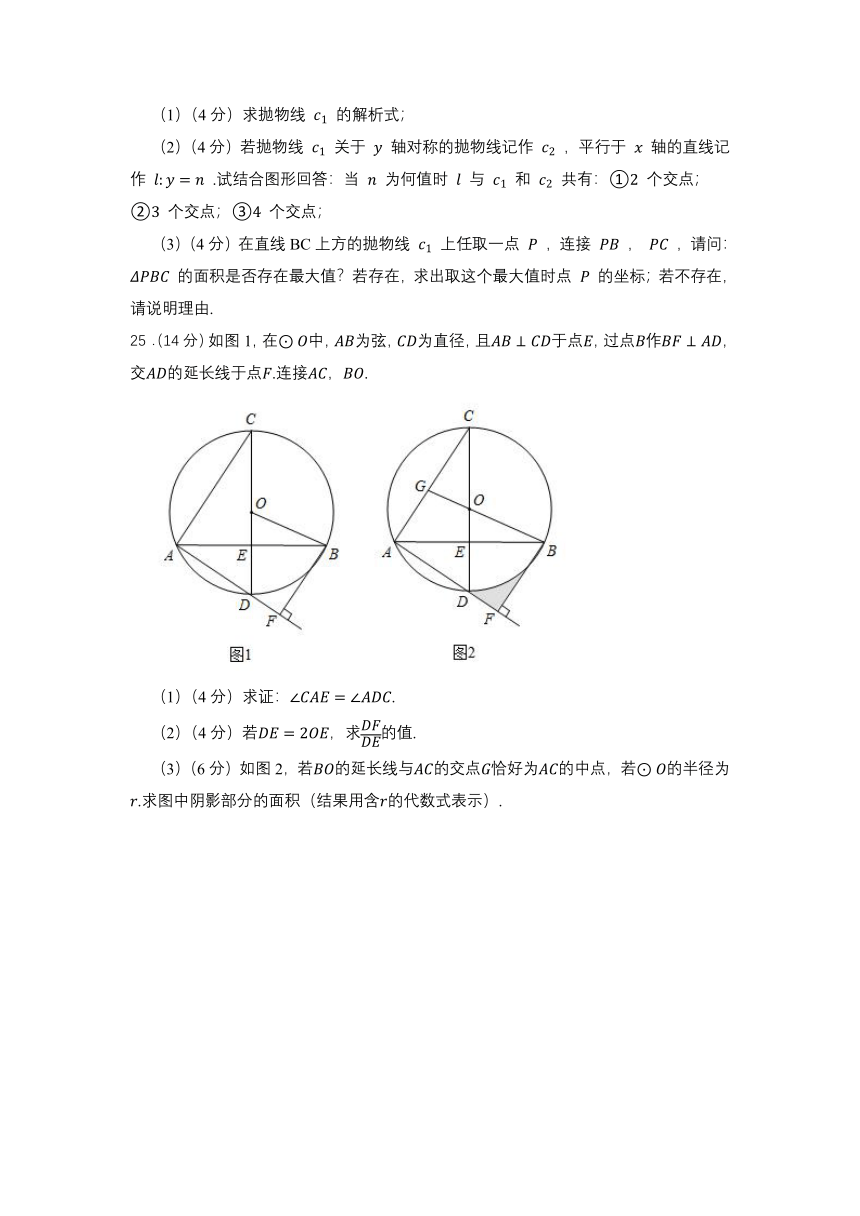
(1)(4分)求抛物线 的解析式;
(2)(4分)若抛物线 关于 轴对称的抛物线记作 ,平行于 轴的直线记作 .试结合图形回答:当 为何值时 与 和 共有:① 个交点;② 个交点;③ 个交点;
(3)(4分)在直线BC上方的抛物线 上任取一点 ,连接 , ,请问: 的面积是否存在最大值?若存在,求出取这个最大值时点 的坐标;若不存在,请说明理由.
25.(14分)如图1,在中,为弦,为直径,且于点,过点作,交的延长线于点.连接,.
(1)(4分)求证:.
(2)(4分)若,求的值.
(3)(6分)如图2,若的延长线与的交点恰好为的中点,若的半径为.求图中阴影部分的面积(结果用含的代数式表示).
答案解析部分
1.【答案】B
【解析】【解答】解:∵单项式 与 的和仍是单项式,
所以这两个单项式是同类项,
∴
解得
∴ .
故答案为:B.
【分析】所谓同类项就是所含字母相同,而且相同字母的指数也分别相同的项,同类项与字母的顺序及系数没有关系,据此可得m-2=3,7-2n=3,求出m、n的值,进而可得n2-m2的值.
2.【答案】C
【解析】【解答】解:∵a>0,b<0,|a|<|b|,
∴原式=a﹣b﹣|a|
=a﹣b﹣a
=﹣b.
故选C.
【分析】由数轴可得到a>0,b<0,|a|<|b|,根据 =|a|和绝对值的性质即可得到答案.
3.【答案】B
【解析】【解答】解:A.了解20万只节能灯的使用寿命,具有破坏性,适合抽样调查,故本选项不合题意;
B.了解某班35名学生的视力情况,人员不多,适合用全面调查,故本选项符合题意;
C.了解某条河流的水质情况,范围广,适合抽样调查,故本选项不合题意;
D.了解全国居民对“垃圾分类”有关内容的认识程度,范围广,适合抽样调查,故本选项不合题意;
故答案为:B.
【分析】根据全面调查的定义对每个选项一一判断即可。
4.【答案】B
【解析】【解答】解:∵,
∴函数的图象在第二、四象限,在每一象限内,随的增大而增大,
①当点、在图象的同一支上,
∵,∴,此不等式无解;
②当点、在图象的两支上,
∵,∴,,解得:,
故选:B.
【分析】由反比例函数的图象与系数的关系得出函数的图象在第二、四象限,在每一象限内,随的增大而增大,然后分两种情况讨论,①当点、在图象的同一支上,②当点、在图象的两支上,依此分别列出不等式求解,即可解答.
5.【答案】A
【解析】【分析】由两圆的半径分别是方程x2-4x+3=0的两根,利用因式分解法即可求得两圆的半径,又由两圆的圆心距为3,即可求得这两个圆的位置关系.
【解答】∵x2-4x+3=0,
∴(x-1)(x-3)=0,
解得:x1=1,x2=3,
∴两圆的半径分别是1,3,
∵1+3=4>3,3-1=2<3,
∴这两个圆的位置关系是:相交.
故答案为:A
6.【答案】D
【解析】【解答】解:选项A、算术平方根是自身的数有0和1,故该选项不符合题意;
B、 ×|-1|×1不是最简二次根式,故该选项不符合题意;
C、只有一个角是60°的三角形不一定是等边三角形,故该选项不符合题意;
D、三角形的内角和等于180度,故该选项符合题意,
故答案为:D.
【分析】根据真命题的定义对每个选项一一判断即可。
7.【答案】
【解析】【解答】 的相反数是
故答案为:
【分析】相反数的定义:只有符号不同的两个数互为相反数;负数的相反数是正数.
8.【答案】ab(1﹣b)
【解析】【解答】解:ab﹣ab2=ab(1﹣b).
故答案为:ab(1﹣b).
【分析】直接提取公因式ab即可分解因式得出答案.
9.【答案】x=3
【解析】【解答】解:依题意得,x﹣1=0或x﹣3=0,
∴x=1或x=3,
当x=1时,x﹣3<0,
∴x=1不合题意,舍去,
∴x=3,
故答案为:x=3.
【分析】根据题意可得x﹣1=0或x﹣3=0,再求出x的值即可。
10.【答案】
【解析】【解答】掷一次骰子可能出现的点数为1,2,3,4,5,6,其中是2 的倍数的情况为2,4,6.
故概率为P= .
【分析】先求出掷一次骰子所有的情况,再用目标的情况个数除以总数即可求出该事件的概率.
11.【答案】③④
【解析】【解答】∵抛物线y=ax2+bx+c的开口向上,
∴a>0,
又∵对称轴 ,
∴b<0
∴结论①是错误的;
∵x=-1时,y>0,
∴a-b+c>0,
∴结论②是错误的;
∵抛物线向右平移了2个单位,
∴平行四边形的底是2,
∵函数y=ax2+bx+c的最小值是y=-2,
∴平行四边形的高是2,
∴阴影部分的面积是 ,
∴结论③是正确的;
∵ ,c=-1,
∴b2=4a,
∴结论④是正确的;
故答案是③④。
【分析】①首先根据抛物线开口向上,可得a>0;然后根据对称轴为x=->0,可得b<0,据此判断即可;
②根据抛物线y=ax2+bx+c的图象,可得x=-1时,y>0,即a-b+c>0,据此判断即可;
③首先判断出阴影部分是一个平行四边形,然后根据平行四边形的面积=底×高,求出阴影部分的面积是多少即可.
④根据函数的最小值是=-2,可求出c的值,就可得出a、b的关系。综上所述,就可得出答案。
12.【答案】
【解析】【解答】解:;
故答案是:.
【分析】直接利用平方差公式分解即可.
13.【答案】
【解析】【解答】解:∵=,=,
∴=﹣=﹣,
∵在△ABC中,D、E分别是边AB、边AC的中点,
∴==(﹣)=﹣.
故答案为:
【分析】由=,=,利用三角形法则求解即可求得,又由在△ABC中,D、E分别是边AB、边AC的中点,可得DE是△ABC的中位线,然后利用三角形中位线的性质求解即可求得答案.
14.【答案】6
【解析】【解答】解:由题意可得: =6,可知:x=6,
将该数据从小到大排列得:4,5,6,6,7,8,故中位数为 =6,故答案为6.
【分析】利用平均数的计算方法求出x的值,再将这6个数从小到大排列,可知最中间的两个数为6、6,求出这两个数的平均数,就可得出这组数据的中位数。
15.【答案】1.5×106
【解析】【解答】将1 500 000 用科学记数法表示为:1.5×106.
故答案为:1.5×106.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
16.【答案】
【解析】【解答】解:连接OE,
设∠DOE的度数为,
由题意得:,
解得:,即°,
∴,
∵以CD为直径的半圆与AB,AC相切于E,C两点,
∴,,
∴,
∵
∴,,
∴,
则,
∴,
故答案为:.
【分析】连接OE,根据弧长公式求出∠DOE,根据切线的性质得出,,解直角三角形求出BE、AC,根据扇形面积公式、三角形面积公式计算即可。
17.【答案】 π
【解析】【解答】解:∵AM垂直于直线BP,∴∠BMA=90°,∴点M的路径是以AB的中点N为圆心,AB长的一半为半径的弧OA,连接ON.
∵直线y=﹣x+4与两坐标轴交A、B两点,∴OA=OB=4,∴ON⊥AB,∴∠ONA=90°.∵AB= =4 ,∴ON=2 ,∴弧OA的长= 2 = .故答案为: π.
【分析】由于在运动的过程中∠BMA=90°始终没变,根据圆周角定理点M的路径是以AB的中点N为圆心,AB长的一半为半径的弧OA,连接ON.根据直线与坐标轴交点的坐标特点得出A,B两点的坐标,进而得出OA,OB的长度,根据勾股定理得出AB的长度,根据直角三角形斜边上的中线等于斜边的一半得出ON的长,根据等腰三角形的三线合一得出∠ONA的度数,根据弧长公式即可得出答案。
18.【答案】5
【解析】【解答】解:如图,连接OC,设圆的半径为x,
由垂径定理可得:CH=CD=4,
Rt△OCH中,OH=AH-AO=8-x,则
,
,
解得:x=5,即⊙O半径为5,
故答案为:5;
【分析】连接OC,设圆的半径为x,利用垂径定理和勾股定理可得,再求出x的值即可。
19.【答案】解:
= ÷( + )
= ÷
= ×
= ,
把 ,代入原式= = = =
【解析】【分析】分式的化简,要熟悉混合运算的顺序,分子、分母能因式分解的先因式分解;除法要统一为乘法运算,注意化简后,将 ,代入化简后的式子求出即可.
20.【答案】解:,
解不等式得:,
解不等式得:,
不等式组的解集是,
在数轴上表示为:
.
【解析】【分析】利用不等式的性质及不等式组的解法求出解集并在数轴上画出解集即可。
21.【答案】(1)解:如图,连接BD,
∵∠BAD=90°,
∴点O必在BD上,即:BD是直径,
∴∠BCD=90°,
∴∠DEC+∠CDE=90°,
∵∠DEC=∠BAC,
∴∠BAC+∠CDE=90°,
∵∠BAC=∠BDC,
∴∠BDC+∠CDE=90°,
∴∠BDE=90°,即:BD⊥DE,
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)解:∵∠BAF=∠BDE=90°,
∴∠F+∠ABC=∠FDE+∠ADB=90°,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ADB=∠ACB,
∴∠F=∠EDF,
∴DE=EF=6,
∵CE=4,∠BCD=90°,
∴∠DCE=90°,
∴CD= ,
∵∠BDE=90°,CD⊥BE,
∴△CDE∽△CBD,
∴,
∴BD,
∴⊙O的半径=.
【解析】【分析】(1)先判断出BD是直径,再判断出BD⊥DE,即可得出结论;
(2)根据余角的性质和等腰三角形的性质得出∠F=∠EDF,根据等腰三角形的性质得出DE=EF=6,根据勾股定理得出CD= ,根据相似三角形的性质即可得出结论。
22.【答案】(1)解:在Rt△ANM中,∵∠NAM=45°,
∴AM=MN,
在Rt△BMN中,∵∠MBN=60°,
∴BM= ,
∵AB=AM+BM=(1+ )MN=27.3,
∴MN=30.1米,
答:钟楼MN的高度为30.1米;
(2)解:不正确,
理由:在Rt△CNM中,∵∠NCM=75°,MN=30,
∴CM= ≈8≠5
【解析】【分析】(1)在等腰直角三角形ANM中,AM=MN,在直角三角形BMN中,由tan∠MBN=可将BM用含MN的代数式表示出来,由图知: AB=AM+BM ,于是可得关于MN的方程,解方程可求得MN的长;
(2)解直角三角形即可求解。
23.【答案】(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,理由如下:
∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形
(3)解:若D为AB中点,则当∠A=45°时,四边形BECD是正方形,理由如下:
∵∠A=45°,∠ACB=90°,
∴∠ABC=45°,
∵四边形BECD是菱形,
∴DC=DB,
∴∠DBC=∠DCB=45°,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴四边形BECD是正方形.
【解析】【分析】(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;(3)四边形BECD为正方形,则∠ADE=∠BDE=45°,可得∠ABC=45°,则∠A=45°.
24.【答案】(1)解:∵抛物线 经过点 和点 ,则
解得
∴抛物线 的解析式为 .
(2)解:由图可知,
① 时有2个交点;
② 时有3个交点;
③ 或 时,有4个交点
(3)解:∵ ,可设直线BC的方程为 ,将 代入可得 ,∴直线BC的方程为 .
过P作 轴交直线BC于点Q,交 轴于点E,如图.
设 , ,
,
,
,
故有
,
,
,
,
,
∴当 时, 有最大值 ,此时P点坐标为 ,
∴当P点坐标为 时, 的面积有最大值.
【解析】【分析】(1)由题意用待定系数法可求得抛物线解析式;
(2)根据轴对称的性质得到抛物线c2的解析式为:y= 2x2 12x 10,结合图象即可求解;
(3)用待定系数法可求得直线BC解析式,过P作PQ∥y轴,交直线BC于点Q,可设出P、Q的坐标 , ,然后用含x的的代数式表示S△PBC,并将解析式配成顶点式,根据二次函数的性质可求得其最大值,则P点坐标可求解.
25.【答案】(1)证明:∵为直径,
∴,即,
又∵,
∴,
∴
(2)解:如下图,连接,
∵,,
∴,
设,则,,
∴在中,,
∴在中,,
∵为直径,且,
∴,
∴,
∴,
∴,
又∵,
∴,
∵,
∴,
∴,即,
解得,
∴;
(3)解:如下图,连接,
∵的延长线与的交点恰好为的中点,
∴,即,
∴,
∴,
又∵,,
∴,
∴,
∵为直径,,
∴,
∴,
∴,即为等边三角形,,
∵的半径为,
∴,,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴
.
【解析】【分析】(1)由圆周角定理可得∠CAD=90°,根据垂直的概念可得∠AED=90°,然后根据同角的余角相等可得结论;
(2)连接BD,则OD=3OE,设OE=a,则DE=2a,OB=OD=3a,由勾股定理可得BE、BD,根据垂径定理可得BE=AE,则AD=BD,根据等腰三角形的性质以及外角的性质可得∠BDF=2∠DAB,由圆周角定理可得∠DOB=2∠DAB=∠BDF,证明△BOE∽△BDF,根据相似三角形的性质可得DF,据此求解;
(3)连接BD,利用ASA证明△OBE≌△DAE,得到OB=DA,根据弧、弦的关系可得DA=DB,推出△OBD为等边三角形,得到∠BOD=60°,设半径为r,则OB=r,OE=DE=r,BE=r,AB=r,由圆周角定理可得∠BAD=30°,则BF=r,AF=r,根据全等三角形的性质可得S△OBE=S△DAE,推出S阴影=S△ABF-S扇形OBD,据此计算.
一、单选题(共6题;共24分)
1.(4分)若单项式 与 的和仍是单项式,则 的值为( )
A.21 B.-21 C.29 D.-29
2.(4分)实数a、b在数轴上的位置如图所示,那么化简|a﹣b|﹣ 的结果是( )
A.2a﹣b B.b C.﹣b D.﹣2a+b
3.(4分)下列调查中,适合用全面调查的是()
A.了解20万只节能灯的使用寿命
B.了解某班35名学生的视力情况
C.了解某条河流的水质情况
D.了解全国居民对“垃圾分类”有关内容的认识程度
4.(4分)若点,在反比例函数的图象上,且,则m的取值范围是( )
A. B.
C. D.或
5.(4分)若两圆的圆心距为3,两圆的半径分别是方程x2-4x+3=0的两个根,则两圆的位置关 系是 ( )
A.相交 B.外离 C.内含 D.外切
6.(4分)下列命题中,是真命题的是( )
A.算术平方根等于自身的数只有1
B. ×|﹣1|×1是最简二次根式
C.只有一个角等于60°的三角形是等边三角形
D.三角形内角和等于180度
二、填空题(共12题;共48分)
7.(4分) 的相反数是 .
8.(4分)分解因式:ab﹣ab2= .
9.(4分)方程=0的根是 .
10.(4分)一枚质地均匀的正方体骰子,六个面分别刻有 到 的点数,小涛同学掷一次骰子,骰子的正面朝上的点数是 的倍数的概率是 .
11.(4分)已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是 .(写出所有正确结论的序号)①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
12.(4分)在实数范围内分解因式= .
13.(4分)如图,已知在△ABC中,D、E分别是边AB、边AC的中点,=,=,那么向量用向量,表示为 .
14.(4分)为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的6名同学捐书册数分别是:5,7,x,8,4,6.已知他们平均每人捐6本,则这组数据的中位数是 .
15.(4分)为鼓励大学生创业,某市为在开发区创业的每位大学生提供贷款1500000 元,这个数据用科学记数法表示为 元.
16.(4分)如图,以CD为直径的半圆与AB,AC相切于E,C两点,C,D,B三点共线,若弧DE的长为,CD=2,则阴影部分的面积为 .
17.(4分)如图,直线y=﹣x+4与两坐标轴交A、B两点,点P为线段OA上的动点,连接BP,过点A作AM垂直于直线BP,垂足为M,当点P从点O运动到点A时,则点M运动路径的长为 .
18.(4分)如图,在⊙O中,AB为直径,弦于点H,若,则⊙O的半径长为 .
三、解答题(共7题;共78分)
19.(10分)先化简,再求值: ÷(1+ ),其中x= ﹣1.
20.(10分)解不等式组:,并把解集在数轴上表示出来.
21.(10分)如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)(5分)求证:DE是⊙O的切线;
(2)(5分)当AB=AC时,若CE=4,EF=6,求⊙O的半径.
22.(10分)如图,小聪和小明在校园内测量钟楼MN的高度.小聪在A处测得钟楼顶端N的仰角为45°,小明在B处测得钟楼顶端N的仰角为60°,并测得A,B两点之间的距离为27.3米,已知点A,M,B依次在同一直线上.
(1)(5分)求钟楼MN的高度,(结果精确到0.1米)
(2)(5分)因为要举办艺术节,学校在钟楼顶端N处拉了一条宣传竖幅,并固定在地面上的C处(点C在线段AM上).小聪测得点C处的仰角∠NCM等于75°,小明测得点C,M之间的距离约为5米,若小聪的仰角数据正确,问小明测得的数据“5米”是否正确?为什么?(参考数据: 1.41, 1.73)
23.(12分)如图,在Rt△ABC中,∠ACB=90,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE
(1)(4分)求证:CE=AD
(2)(4分)当点D在AB中点时,四边形BECD是什么特殊四边形?说明理由
(3)(4分)若D为AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?说明理由.
24.(12分) 经过点 和点 ,与 轴交于点C.
(1)(4分)求抛物线 的解析式;
(2)(4分)若抛物线 关于 轴对称的抛物线记作 ,平行于 轴的直线记作 .试结合图形回答:当 为何值时 与 和 共有:① 个交点;② 个交点;③ 个交点;
(3)(4分)在直线BC上方的抛物线 上任取一点 ,连接 , ,请问: 的面积是否存在最大值?若存在,求出取这个最大值时点 的坐标;若不存在,请说明理由.
25.(14分)如图1,在中,为弦,为直径,且于点,过点作,交的延长线于点.连接,.
(1)(4分)求证:.
(2)(4分)若,求的值.
(3)(6分)如图2,若的延长线与的交点恰好为的中点,若的半径为.求图中阴影部分的面积(结果用含的代数式表示).
答案解析部分
1.【答案】B
【解析】【解答】解:∵单项式 与 的和仍是单项式,
所以这两个单项式是同类项,
∴
解得
∴ .
故答案为:B.
【分析】所谓同类项就是所含字母相同,而且相同字母的指数也分别相同的项,同类项与字母的顺序及系数没有关系,据此可得m-2=3,7-2n=3,求出m、n的值,进而可得n2-m2的值.
2.【答案】C
【解析】【解答】解:∵a>0,b<0,|a|<|b|,
∴原式=a﹣b﹣|a|
=a﹣b﹣a
=﹣b.
故选C.
【分析】由数轴可得到a>0,b<0,|a|<|b|,根据 =|a|和绝对值的性质即可得到答案.
3.【答案】B
【解析】【解答】解:A.了解20万只节能灯的使用寿命,具有破坏性,适合抽样调查,故本选项不合题意;
B.了解某班35名学生的视力情况,人员不多,适合用全面调查,故本选项符合题意;
C.了解某条河流的水质情况,范围广,适合抽样调查,故本选项不合题意;
D.了解全国居民对“垃圾分类”有关内容的认识程度,范围广,适合抽样调查,故本选项不合题意;
故答案为:B.
【分析】根据全面调查的定义对每个选项一一判断即可。
4.【答案】B
【解析】【解答】解:∵,
∴函数的图象在第二、四象限,在每一象限内,随的增大而增大,
①当点、在图象的同一支上,
∵,∴,此不等式无解;
②当点、在图象的两支上,
∵,∴,,解得:,
故选:B.
【分析】由反比例函数的图象与系数的关系得出函数的图象在第二、四象限,在每一象限内,随的增大而增大,然后分两种情况讨论,①当点、在图象的同一支上,②当点、在图象的两支上,依此分别列出不等式求解,即可解答.
5.【答案】A
【解析】【分析】由两圆的半径分别是方程x2-4x+3=0的两根,利用因式分解法即可求得两圆的半径,又由两圆的圆心距为3,即可求得这两个圆的位置关系.
【解答】∵x2-4x+3=0,
∴(x-1)(x-3)=0,
解得:x1=1,x2=3,
∴两圆的半径分别是1,3,
∵1+3=4>3,3-1=2<3,
∴这两个圆的位置关系是:相交.
故答案为:A
6.【答案】D
【解析】【解答】解:选项A、算术平方根是自身的数有0和1,故该选项不符合题意;
B、 ×|-1|×1不是最简二次根式,故该选项不符合题意;
C、只有一个角是60°的三角形不一定是等边三角形,故该选项不符合题意;
D、三角形的内角和等于180度,故该选项符合题意,
故答案为:D.
【分析】根据真命题的定义对每个选项一一判断即可。
7.【答案】
【解析】【解答】 的相反数是
故答案为:
【分析】相反数的定义:只有符号不同的两个数互为相反数;负数的相反数是正数.
8.【答案】ab(1﹣b)
【解析】【解答】解:ab﹣ab2=ab(1﹣b).
故答案为:ab(1﹣b).
【分析】直接提取公因式ab即可分解因式得出答案.
9.【答案】x=3
【解析】【解答】解:依题意得,x﹣1=0或x﹣3=0,
∴x=1或x=3,
当x=1时,x﹣3<0,
∴x=1不合题意,舍去,
∴x=3,
故答案为:x=3.
【分析】根据题意可得x﹣1=0或x﹣3=0,再求出x的值即可。
10.【答案】
【解析】【解答】掷一次骰子可能出现的点数为1,2,3,4,5,6,其中是2 的倍数的情况为2,4,6.
故概率为P= .
【分析】先求出掷一次骰子所有的情况,再用目标的情况个数除以总数即可求出该事件的概率.
11.【答案】③④
【解析】【解答】∵抛物线y=ax2+bx+c的开口向上,
∴a>0,
又∵对称轴 ,
∴b<0
∴结论①是错误的;
∵x=-1时,y>0,
∴a-b+c>0,
∴结论②是错误的;
∵抛物线向右平移了2个单位,
∴平行四边形的底是2,
∵函数y=ax2+bx+c的最小值是y=-2,
∴平行四边形的高是2,
∴阴影部分的面积是 ,
∴结论③是正确的;
∵ ,c=-1,
∴b2=4a,
∴结论④是正确的;
故答案是③④。
【分析】①首先根据抛物线开口向上,可得a>0;然后根据对称轴为x=->0,可得b<0,据此判断即可;
②根据抛物线y=ax2+bx+c的图象,可得x=-1时,y>0,即a-b+c>0,据此判断即可;
③首先判断出阴影部分是一个平行四边形,然后根据平行四边形的面积=底×高,求出阴影部分的面积是多少即可.
④根据函数的最小值是=-2,可求出c的值,就可得出a、b的关系。综上所述,就可得出答案。
12.【答案】
【解析】【解答】解:;
故答案是:.
【分析】直接利用平方差公式分解即可.
13.【答案】
【解析】【解答】解:∵=,=,
∴=﹣=﹣,
∵在△ABC中,D、E分别是边AB、边AC的中点,
∴==(﹣)=﹣.
故答案为:
【分析】由=,=,利用三角形法则求解即可求得,又由在△ABC中,D、E分别是边AB、边AC的中点,可得DE是△ABC的中位线,然后利用三角形中位线的性质求解即可求得答案.
14.【答案】6
【解析】【解答】解:由题意可得: =6,可知:x=6,
将该数据从小到大排列得:4,5,6,6,7,8,故中位数为 =6,故答案为6.
【分析】利用平均数的计算方法求出x的值,再将这6个数从小到大排列,可知最中间的两个数为6、6,求出这两个数的平均数,就可得出这组数据的中位数。
15.【答案】1.5×106
【解析】【解答】将1 500 000 用科学记数法表示为:1.5×106.
故答案为:1.5×106.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
16.【答案】
【解析】【解答】解:连接OE,
设∠DOE的度数为,
由题意得:,
解得:,即°,
∴,
∵以CD为直径的半圆与AB,AC相切于E,C两点,
∴,,
∴,
∵
∴,,
∴,
则,
∴,
故答案为:.
【分析】连接OE,根据弧长公式求出∠DOE,根据切线的性质得出,,解直角三角形求出BE、AC,根据扇形面积公式、三角形面积公式计算即可。
17.【答案】 π
【解析】【解答】解:∵AM垂直于直线BP,∴∠BMA=90°,∴点M的路径是以AB的中点N为圆心,AB长的一半为半径的弧OA,连接ON.
∵直线y=﹣x+4与两坐标轴交A、B两点,∴OA=OB=4,∴ON⊥AB,∴∠ONA=90°.∵AB= =4 ,∴ON=2 ,∴弧OA的长= 2 = .故答案为: π.
【分析】由于在运动的过程中∠BMA=90°始终没变,根据圆周角定理点M的路径是以AB的中点N为圆心,AB长的一半为半径的弧OA,连接ON.根据直线与坐标轴交点的坐标特点得出A,B两点的坐标,进而得出OA,OB的长度,根据勾股定理得出AB的长度,根据直角三角形斜边上的中线等于斜边的一半得出ON的长,根据等腰三角形的三线合一得出∠ONA的度数,根据弧长公式即可得出答案。
18.【答案】5
【解析】【解答】解:如图,连接OC,设圆的半径为x,
由垂径定理可得:CH=CD=4,
Rt△OCH中,OH=AH-AO=8-x,则
,
,
解得:x=5,即⊙O半径为5,
故答案为:5;
【分析】连接OC,设圆的半径为x,利用垂径定理和勾股定理可得,再求出x的值即可。
19.【答案】解:
= ÷( + )
= ÷
= ×
= ,
把 ,代入原式= = = =
【解析】【分析】分式的化简,要熟悉混合运算的顺序,分子、分母能因式分解的先因式分解;除法要统一为乘法运算,注意化简后,将 ,代入化简后的式子求出即可.
20.【答案】解:,
解不等式得:,
解不等式得:,
不等式组的解集是,
在数轴上表示为:
.
【解析】【分析】利用不等式的性质及不等式组的解法求出解集并在数轴上画出解集即可。
21.【答案】(1)解:如图,连接BD,
∵∠BAD=90°,
∴点O必在BD上,即:BD是直径,
∴∠BCD=90°,
∴∠DEC+∠CDE=90°,
∵∠DEC=∠BAC,
∴∠BAC+∠CDE=90°,
∵∠BAC=∠BDC,
∴∠BDC+∠CDE=90°,
∴∠BDE=90°,即:BD⊥DE,
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)解:∵∠BAF=∠BDE=90°,
∴∠F+∠ABC=∠FDE+∠ADB=90°,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ADB=∠ACB,
∴∠F=∠EDF,
∴DE=EF=6,
∵CE=4,∠BCD=90°,
∴∠DCE=90°,
∴CD= ,
∵∠BDE=90°,CD⊥BE,
∴△CDE∽△CBD,
∴,
∴BD,
∴⊙O的半径=.
【解析】【分析】(1)先判断出BD是直径,再判断出BD⊥DE,即可得出结论;
(2)根据余角的性质和等腰三角形的性质得出∠F=∠EDF,根据等腰三角形的性质得出DE=EF=6,根据勾股定理得出CD= ,根据相似三角形的性质即可得出结论。
22.【答案】(1)解:在Rt△ANM中,∵∠NAM=45°,
∴AM=MN,
在Rt△BMN中,∵∠MBN=60°,
∴BM= ,
∵AB=AM+BM=(1+ )MN=27.3,
∴MN=30.1米,
答:钟楼MN的高度为30.1米;
(2)解:不正确,
理由:在Rt△CNM中,∵∠NCM=75°,MN=30,
∴CM= ≈8≠5
【解析】【分析】(1)在等腰直角三角形ANM中,AM=MN,在直角三角形BMN中,由tan∠MBN=可将BM用含MN的代数式表示出来,由图知: AB=AM+BM ,于是可得关于MN的方程,解方程可求得MN的长;
(2)解直角三角形即可求解。
23.【答案】(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,理由如下:
∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形
(3)解:若D为AB中点,则当∠A=45°时,四边形BECD是正方形,理由如下:
∵∠A=45°,∠ACB=90°,
∴∠ABC=45°,
∵四边形BECD是菱形,
∴DC=DB,
∴∠DBC=∠DCB=45°,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴四边形BECD是正方形.
【解析】【分析】(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;(3)四边形BECD为正方形,则∠ADE=∠BDE=45°,可得∠ABC=45°,则∠A=45°.
24.【答案】(1)解:∵抛物线 经过点 和点 ,则
解得
∴抛物线 的解析式为 .
(2)解:由图可知,
① 时有2个交点;
② 时有3个交点;
③ 或 时,有4个交点
(3)解:∵ ,可设直线BC的方程为 ,将 代入可得 ,∴直线BC的方程为 .
过P作 轴交直线BC于点Q,交 轴于点E,如图.
设 , ,
,
,
,
故有
,
,
,
,
,
∴当 时, 有最大值 ,此时P点坐标为 ,
∴当P点坐标为 时, 的面积有最大值.
【解析】【分析】(1)由题意用待定系数法可求得抛物线解析式;
(2)根据轴对称的性质得到抛物线c2的解析式为:y= 2x2 12x 10,结合图象即可求解;
(3)用待定系数法可求得直线BC解析式,过P作PQ∥y轴,交直线BC于点Q,可设出P、Q的坐标 , ,然后用含x的的代数式表示S△PBC,并将解析式配成顶点式,根据二次函数的性质可求得其最大值,则P点坐标可求解.
25.【答案】(1)证明:∵为直径,
∴,即,
又∵,
∴,
∴
(2)解:如下图,连接,
∵,,
∴,
设,则,,
∴在中,,
∴在中,,
∵为直径,且,
∴,
∴,
∴,
∴,
又∵,
∴,
∵,
∴,
∴,即,
解得,
∴;
(3)解:如下图,连接,
∵的延长线与的交点恰好为的中点,
∴,即,
∴,
∴,
又∵,,
∴,
∴,
∵为直径,,
∴,
∴,
∴,即为等边三角形,,
∵的半径为,
∴,,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴
.
【解析】【分析】(1)由圆周角定理可得∠CAD=90°,根据垂直的概念可得∠AED=90°,然后根据同角的余角相等可得结论;
(2)连接BD,则OD=3OE,设OE=a,则DE=2a,OB=OD=3a,由勾股定理可得BE、BD,根据垂径定理可得BE=AE,则AD=BD,根据等腰三角形的性质以及外角的性质可得∠BDF=2∠DAB,由圆周角定理可得∠DOB=2∠DAB=∠BDF,证明△BOE∽△BDF,根据相似三角形的性质可得DF,据此求解;
(3)连接BD,利用ASA证明△OBE≌△DAE,得到OB=DA,根据弧、弦的关系可得DA=DB,推出△OBD为等边三角形,得到∠BOD=60°,设半径为r,则OB=r,OE=DE=r,BE=r,AB=r,由圆周角定理可得∠BAD=30°,则BF=r,AF=r,根据全等三角形的性质可得S△OBE=S△DAE,推出S阴影=S△ABF-S扇形OBD,据此计算.
同课章节目录
