2023年广东省中考数学仿真模拟卷(七)课件(共48张PPT)
文档属性
| 名称 | 2023年广东省中考数学仿真模拟卷(七)课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-09 08:38:29 | ||
图片预览










文档简介
(共48张PPT)
仿真模拟卷 触摸最新考情
2023年广东省初中学业水平考试仿真模拟卷(七)
(本试卷满分120分,考试用时90分钟)
班级: 姓名:
学号: 总分:
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列实数中是无理数的是( C )
A.3.14
C
2.新冠病毒的直径是120纳米,1纳米=10-9米,则这种冠状病毒的直径(单位:米)用科学记数法表示为( C )
A.120×10-9
B.1.2×10-6
C.1.2×10-7
D.1.2×10-8
C
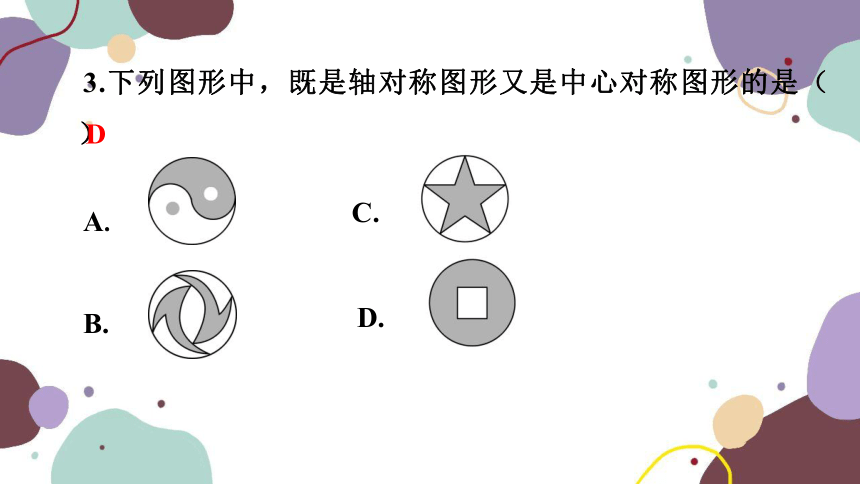
3.下列图形中,既是轴对称图形又是中心对称图形的是( D )
A.
B.
C.
D
D.
4.如图,AB是☉O的直径,点C在圆上,若∠ABC=70°,则∠BAC的度数为( D )
A.70°
B.60°
C.40°
D.20°
D
5.下列各运算中,正确的运算是( B )
B.(2a2)3=8a6
C.a8÷a4=a2
D.(a-b)2=a2-b2
B
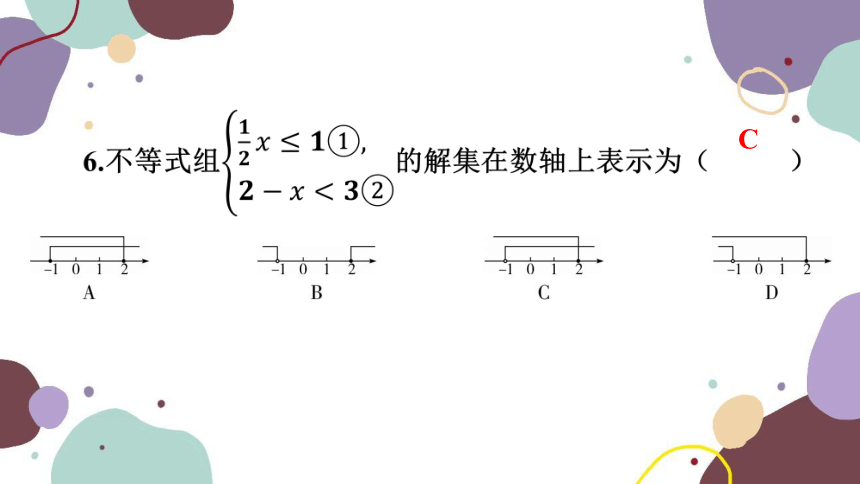
C
7.关于x的方程x2-2x-2=0的根的情况是( A )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法判断根的情况
A
8.如图,将一张矩形纸片折叠,若∠1=80°,则∠2的度数是( A )
A.50°
B.60°
C.70°
D.80°
A
9.如图,点D(0,3),O(0,0),C(4,0)在☉A上,BD是☉A的一条弦,则sin∠OBD=( D )
D
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c-m=0有两个不相等的实数根,下列结论:①b2-4ac<0;②abc>0;③a-b+c<0;④m>-2.其中错误的个数有( B )
A.1
B.2
C.3
D.4
B
0.25
(2a-1)2
x=1
(1,-2)
三、解答题(一):本大题共3小题,每小题8分,共24分.
16.先化简,再求值:(m-n)(m+n)+(m-n)2-2m2.其中m=2,n=1.
解:原式=m2-n2+(m2-2mn+n2)-2m2(4分)
=m2-n2+m2-2mn+n2-2m2
=-2mn.(6分)
当m=2,n=1时,原式=-2×2×1=-4.(8分)
17.如图,在Rt△ABC中,∠C=90°,AC=8.
(1)尺规作图:作∠ABC的平分线交AC于点D;(不写作法,保留作图痕迹)
解:(1)如图,BD即为所求.(4分)
(2)若CD=3,求cos A的值.
解:(2)如图,过点D作DH⊥AB于点H.
18.喜迎2022年10月16日“二十大”的召开,某公司为了贯彻“发展低碳经济,建设美丽中国”的理念,对其生产设备进行了升级改造,不仅提高了产能,而且大幅降低了碳排放量.已知该公司七月的产值为200万元,九月的产值为242万元.
(1)求该公司每月产值的平均增长率;
解:(1)设该公司每月产值的平均增长率为x.
依题意,得 200(1+x)2=242.
解得x1=0.1=10%,x2=-2.1(不合题意,舍去).
答:该公司每月产值的平均增长率为10%.(4分)
(2)按照(1)中平均增长率,求该公司十月的产值.
解:(2)242×(1+10%)=266.2(万元).
答:该公司十月的产值为266.2万元.(8分)
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,在△ABC中,BC>AC,点D在BC边上,且DC=AC, CF是△ACD的高,点E是AB的中点,连接EF.
(2)若四边形BDFE的面积为8,求△AEF的面积.
20.为了让同学们了解自己的体育水平,初三(1)班的体育老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,初三(1)班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
平均分 方差 中位数 众数
男生 7.9 1.99 8 7
女生 7.92 1.993 6 8 8
根据以上信息,解答下列问题:
7.9
8
8
初三(1)班体育模拟测试成绩分析表
(1)这个班共有男生 20 人,共有女生 25 人;
解:(1)提示:这个班共有男生1+2+6+3+5+3=20(人),共有女生45-20=25(人).(2分)
20
25
(2)补全初三(1)班体育模拟测试成绩分析表;
(3)你认为在这次体育测试中,(1)班的男生队、女生队哪个表现更突出一些?并说明理由.(至少从两个不同的角度说明推断的合理性)
解:(3)女生队表现更突出.理由如下:女生队的平均数较高,表示女生队测试成绩较好.女生队的众数较高,女生队的众数为8,中位数也为8,而男生队的众数为7低于中位数8,表示女生队的测试成绩高分较多.(9分)
(1)若点B的坐标是(-3,1),求直线AB的解析式;
解:(1)如图,过点A作AH⊥OC于点H,过点B作BG⊥OC于点G,则AH∥BG.
(2)求△AOC的面积.
(2)点P为抛物线上的点,连接OP交直线DE于点Q,当点Q是OP的中点时,求点P的坐标;
(3)点M在直线DE上,当△CDM为直角三角形时,求出点M的坐标.
①如图2,当∠CMD=90°时,CD2=CM2+DM2.
(2)设△PEF的面积为y(cm2),求y与t之间的函数关系式;
解:(2)如图1,过点A作AG⊥BC于点G.则四边形AGCD是矩形,∠AGB=90°.
(3)连接AP,是否存在某一时刻t,使点E恰好在AP的垂直平分线上?若存在,求出此时t的值;若不存在,请说明理由.
解:(3)存在.理由如下:
如图2,过点P作PH⊥AD于点H.则DH=PC=t,PH=6.
仿真模拟卷 触摸最新考情
2023年广东省初中学业水平考试仿真模拟卷(七)
(本试卷满分120分,考试用时90分钟)
班级: 姓名:
学号: 总分:
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列实数中是无理数的是( C )
A.3.14
C
2.新冠病毒的直径是120纳米,1纳米=10-9米,则这种冠状病毒的直径(单位:米)用科学记数法表示为( C )
A.120×10-9
B.1.2×10-6
C.1.2×10-7
D.1.2×10-8
C
3.下列图形中,既是轴对称图形又是中心对称图形的是( D )
A.
B.
C.
D
D.
4.如图,AB是☉O的直径,点C在圆上,若∠ABC=70°,则∠BAC的度数为( D )
A.70°
B.60°
C.40°
D.20°
D
5.下列各运算中,正确的运算是( B )
B.(2a2)3=8a6
C.a8÷a4=a2
D.(a-b)2=a2-b2
B
C
7.关于x的方程x2-2x-2=0的根的情况是( A )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法判断根的情况
A
8.如图,将一张矩形纸片折叠,若∠1=80°,则∠2的度数是( A )
A.50°
B.60°
C.70°
D.80°
A
9.如图,点D(0,3),O(0,0),C(4,0)在☉A上,BD是☉A的一条弦,则sin∠OBD=( D )
D
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c-m=0有两个不相等的实数根,下列结论:①b2-4ac<0;②abc>0;③a-b+c<0;④m>-2.其中错误的个数有( B )
A.1
B.2
C.3
D.4
B
0.25
(2a-1)2
x=1
(1,-2)
三、解答题(一):本大题共3小题,每小题8分,共24分.
16.先化简,再求值:(m-n)(m+n)+(m-n)2-2m2.其中m=2,n=1.
解:原式=m2-n2+(m2-2mn+n2)-2m2(4分)
=m2-n2+m2-2mn+n2-2m2
=-2mn.(6分)
当m=2,n=1时,原式=-2×2×1=-4.(8分)
17.如图,在Rt△ABC中,∠C=90°,AC=8.
(1)尺规作图:作∠ABC的平分线交AC于点D;(不写作法,保留作图痕迹)
解:(1)如图,BD即为所求.(4分)
(2)若CD=3,求cos A的值.
解:(2)如图,过点D作DH⊥AB于点H.
18.喜迎2022年10月16日“二十大”的召开,某公司为了贯彻“发展低碳经济,建设美丽中国”的理念,对其生产设备进行了升级改造,不仅提高了产能,而且大幅降低了碳排放量.已知该公司七月的产值为200万元,九月的产值为242万元.
(1)求该公司每月产值的平均增长率;
解:(1)设该公司每月产值的平均增长率为x.
依题意,得 200(1+x)2=242.
解得x1=0.1=10%,x2=-2.1(不合题意,舍去).
答:该公司每月产值的平均增长率为10%.(4分)
(2)按照(1)中平均增长率,求该公司十月的产值.
解:(2)242×(1+10%)=266.2(万元).
答:该公司十月的产值为266.2万元.(8分)
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,在△ABC中,BC>AC,点D在BC边上,且DC=AC, CF是△ACD的高,点E是AB的中点,连接EF.
(2)若四边形BDFE的面积为8,求△AEF的面积.
20.为了让同学们了解自己的体育水平,初三(1)班的体育老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,初三(1)班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
平均分 方差 中位数 众数
男生 7.9 1.99 8 7
女生 7.92 1.993 6 8 8
根据以上信息,解答下列问题:
7.9
8
8
初三(1)班体育模拟测试成绩分析表
(1)这个班共有男生 20 人,共有女生 25 人;
解:(1)提示:这个班共有男生1+2+6+3+5+3=20(人),共有女生45-20=25(人).(2分)
20
25
(2)补全初三(1)班体育模拟测试成绩分析表;
(3)你认为在这次体育测试中,(1)班的男生队、女生队哪个表现更突出一些?并说明理由.(至少从两个不同的角度说明推断的合理性)
解:(3)女生队表现更突出.理由如下:女生队的平均数较高,表示女生队测试成绩较好.女生队的众数较高,女生队的众数为8,中位数也为8,而男生队的众数为7低于中位数8,表示女生队的测试成绩高分较多.(9分)
(1)若点B的坐标是(-3,1),求直线AB的解析式;
解:(1)如图,过点A作AH⊥OC于点H,过点B作BG⊥OC于点G,则AH∥BG.
(2)求△AOC的面积.
(2)点P为抛物线上的点,连接OP交直线DE于点Q,当点Q是OP的中点时,求点P的坐标;
(3)点M在直线DE上,当△CDM为直角三角形时,求出点M的坐标.
①如图2,当∠CMD=90°时,CD2=CM2+DM2.
(2)设△PEF的面积为y(cm2),求y与t之间的函数关系式;
解:(2)如图1,过点A作AG⊥BC于点G.则四边形AGCD是矩形,∠AGB=90°.
(3)连接AP,是否存在某一时刻t,使点E恰好在AP的垂直平分线上?若存在,求出此时t的值;若不存在,请说明理由.
解:(3)存在.理由如下:
如图2,过点P作PH⊥AD于点H.则DH=PC=t,PH=6.
同课章节目录
