湖南省永州市2022-2023学年八年级下学期第三次月考数学试题
文档属性
| 名称 | 湖南省永州市2022-2023学年八年级下学期第三次月考数学试题 |  | |
| 格式 | docx | ||
| 文件大小 | 327.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-09 16:20:17 | ||
图片预览

文档简介
第三次课后服务练习(范围:1—4单元)
一.选择题(共12小题)
1.(3分)下列食品标识中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.(3分)下列各组数中,不是勾股数的是( )
A.3,4,5 B.5,12,13 C.7,25,26 D.6,8,10
3.(3分)如图,三角形ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD的长为( )
A.1 B.2 C.2.5 D.3
4.(3分)下列命题是真命题的是( )
A.对角线相等的平行四边形是菱形
B.有一组邻边相等的平行四边形是菱形
C.对角线相互垂直且相等的四边形是菱形
D.有一组对边平行且相等的四边形是菱形
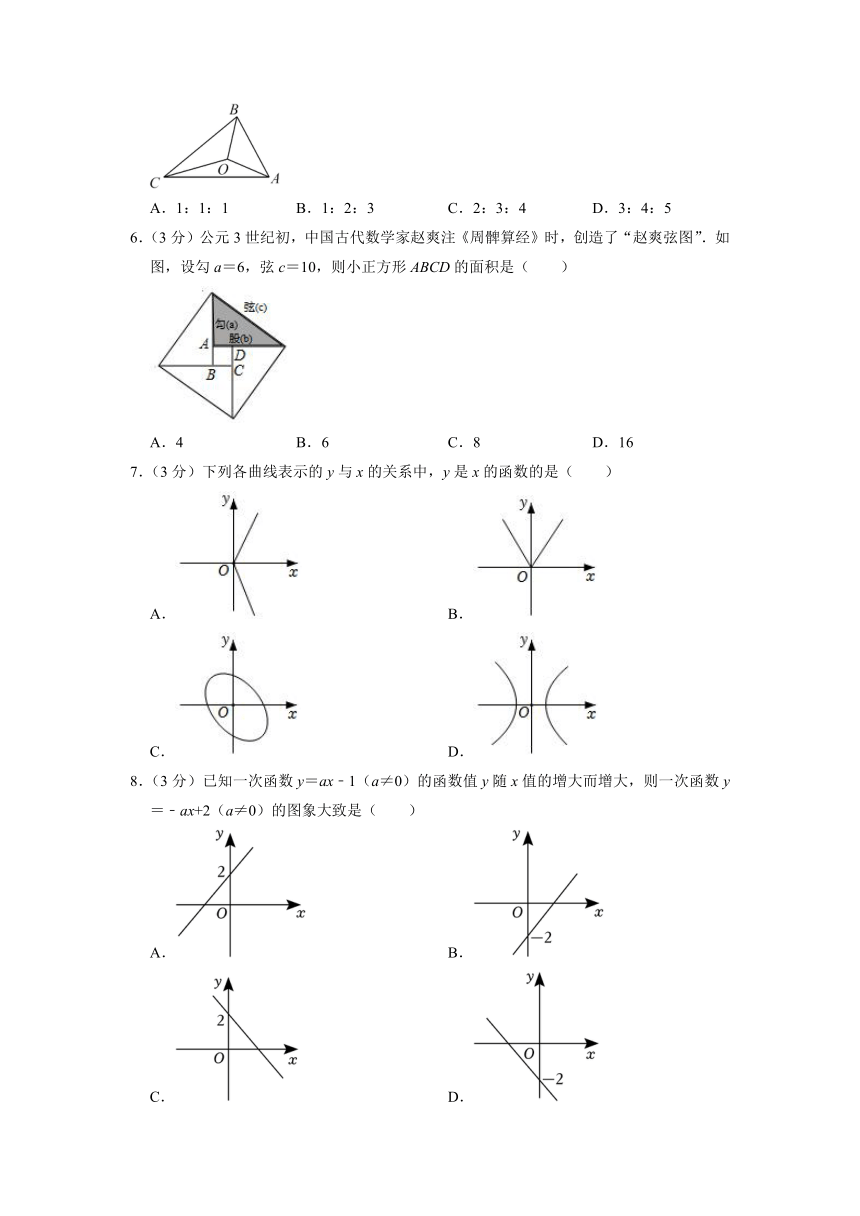
5.(3分)如图,△ABC的三边AB,BC,CA的长分别为20,30,40,O是△ABC三条角平分线的交点,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
6.(3分)公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是( )
A.4 B.6 C.8 D.16
7.(3分)下列各曲线表示的y与x的关系中,y是x的函数的是( )
A. B.
C. D.
8.(3分)已知一次函数y=ax﹣1(a≠0)的函数值y随x值的增大而增大,则一次函数y=﹣ax+2(a≠0)的图象大致是( )
A. B.
C. D.
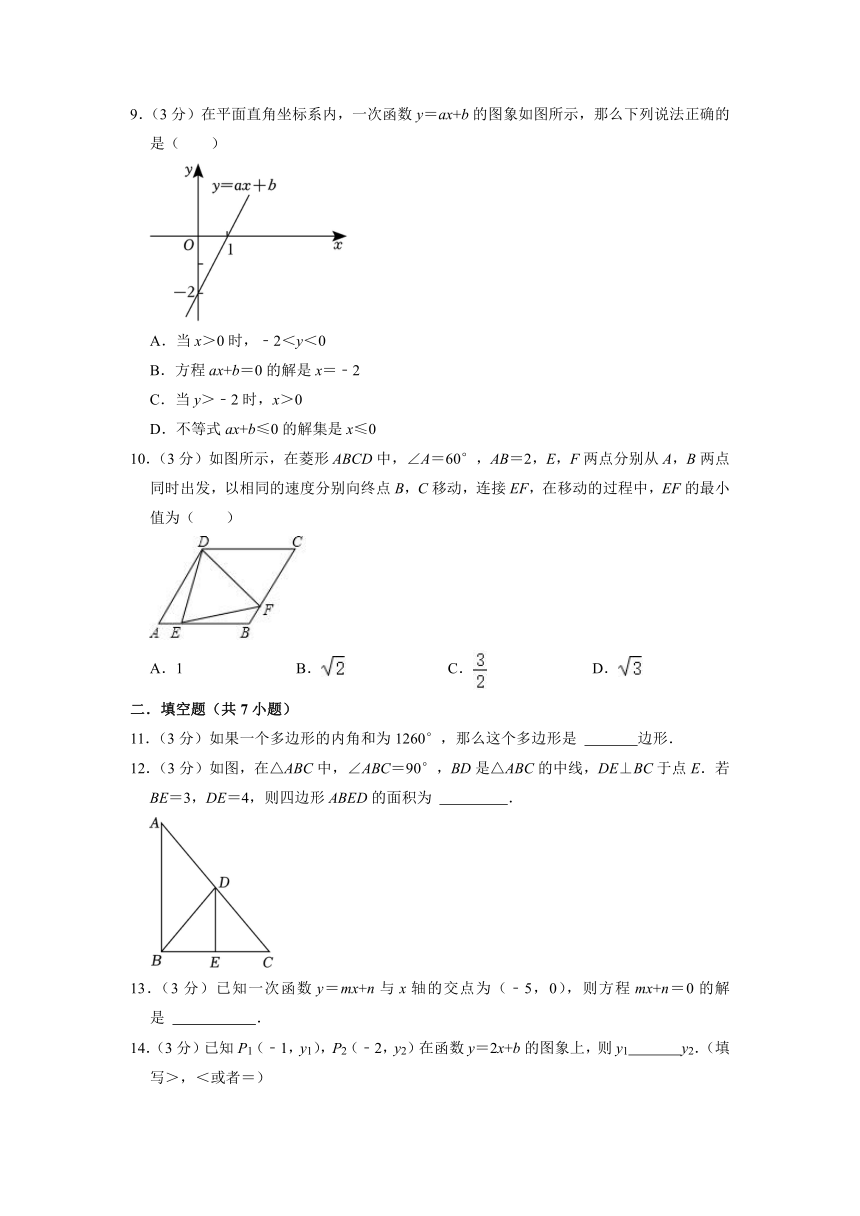
9.(3分)在平面直角坐标系内,一次函数y=ax+b的图象如图所示,那么下列说法正确的是( )
A.当x>0时,﹣2<y<0
B.方程ax+b=0的解是x=﹣2
C.当y>﹣2时,x>0
D.不等式ax+b≤0的解集是x≤0
10.(3分)如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )
A.1 B. C. D.
二.填空题(共7小题)
11.(3分)如果一个多边形的内角和为1260°,那么这个多边形是 边形.
12.(3分)如图,在△ABC中,∠ABC=90°,BD是△ABC的中线,DE⊥BC于点E.若BE=3,DE=4,则四边形ABED的面积为 .
13.(3分)已知一次函数y=mx+n与x轴的交点为(﹣5,0),则方程mx+n=0的解是 .
14.(3分)已知P1(﹣1,y1),P2(﹣2,y2)在函数y=2x+b的图象上,则y1 y2.(填写>,<或者=)
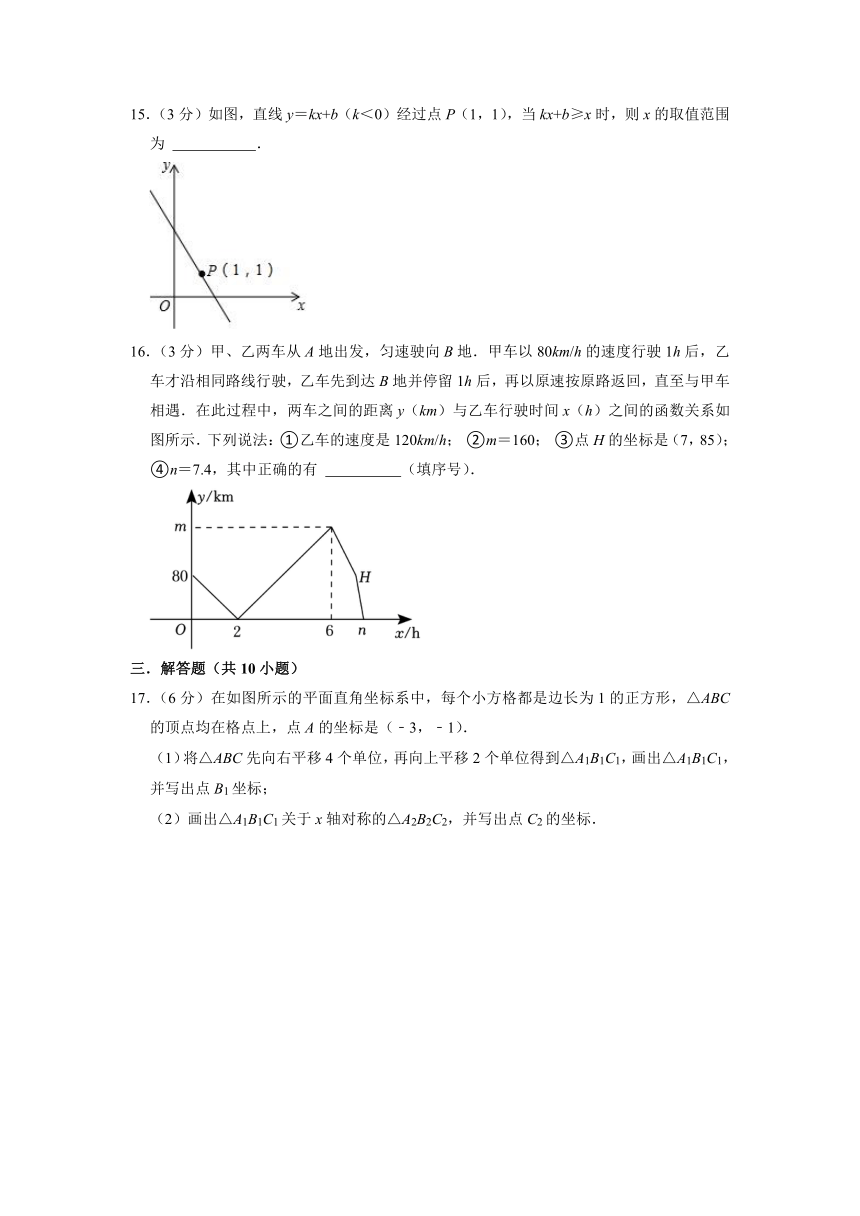
15.(3分)如图,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,则x的取值范围为 .
16.(3分)甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶,乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h; ②m=160; ③点H的坐标是(7,85);④n=7.4,其中正确的有 (填序号).
三.解答题(共10小题)
17.(6分)在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)将△ABC先向右平移4个单位,再向上平移2个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标;
(2)画出△A1B1C1关于x轴对称的△A2B2C2,并写出点C2的坐标.
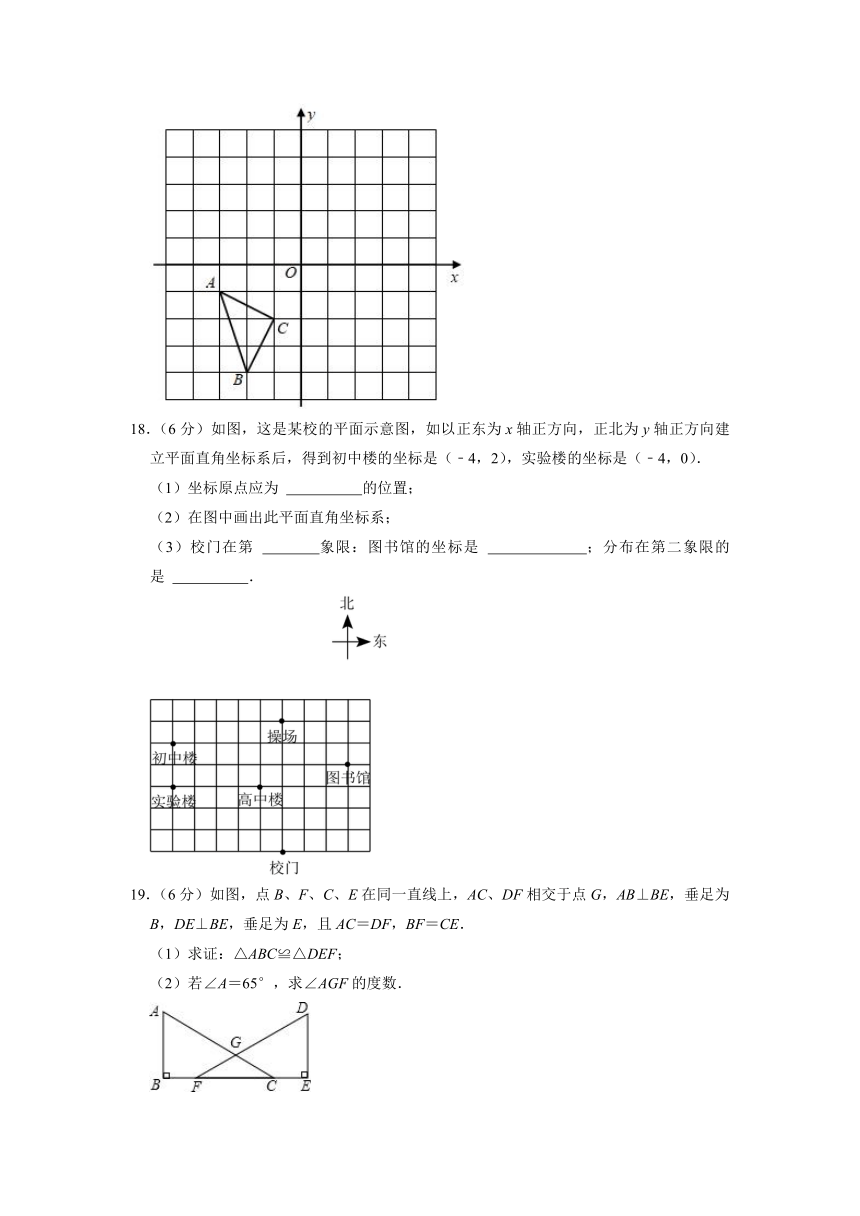
18.(6分)如图,这是某校的平面示意图,如以正东为x轴正方向,正北为y轴正方向建立平面直角坐标系后,得到初中楼的坐标是(﹣4,2),实验楼的坐标是(﹣4,0).
(1)坐标原点应为 的位置;
(2)在图中画出此平面直角坐标系;
(3)校门在第 象限:图书馆的坐标是 ;分布在第二象限的是 .
19.(6分)如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.
(1)求证:△ABC≌△DEF;
(2)若∠A=65°,求∠AGF的度数.
20.(8分)如图,在四边形ABCD中,∠BAC=∠ACD=90°,CD=2AB,E是CD的中点.
(1)求证:四边形ABCE是平行四边形;
(2)若AC=6,AD=10,求 ABCE的面积.
21.(8分)如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,并且DE⊥AB,若AB=4,求:
(1)∠ABC的度数;
(2)对角线AC的长;
(3)菱形ABCD的面积.
22.(9分)已知一次函数y=(1﹣2m)x+m+1;
(1)若一次函数图象经过点P(2,0),求m的值;
(2)若一次函数的图象经过第一、二、三象限;
①求m的取值范围;
②若点M(a﹣1,y1),N(a,y2),在该一次函数的图象上,比较y1和y2大小.
23.(9分)如图, ABCD的对角线AC,BD交于点O,过点D作DE⊥BC于E,延长CB到点F,使BF=CE,连接AF,OF.
(1)求证:四边形AFED是矩形.
(2)若AD=7,BE=2,∠ABF=45°,试求OF的长.
24.(10分)受新冠肺炎疫情影响,一水果种植专业户有大量成熟水果无法出售.“一方有难,八方支援”.某水果经销商主动从该种植专业户购进甲、乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按25元/千克的价格出售.设经销商购进甲种水果x千克,付款y元,y与x之间的函数关系如图所示.
(1)求出当0≤x≤50和x>50时,y与x之间的函数关系式;
(2)若经销商计划一次性购进甲、乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲、乙两种水果的购进量,才能使经销商付款总金额w(元)最少?
25.(10分)如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)求k、b和m的值;
(2)求△ADC的面积;
(3)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由;
(4)若动点P在线段DA上从点D开始以每秒1个单位的速度向点A运动,设点P的运动时间为t秒.是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
第三次课后服务练习(范围:1—4单元)
参考答案与试题解析
一.选择题(共12小题)
1.(3分)下列食品标识中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【考点】中心对称图形;轴对称图形.
【解答】解:A.不是轴对称图形,也不是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.不是轴对称图形,是中心对称图形,故此选项不合题意;
D.既是轴对称图形又是中心对称图形,故此选项符合题意.
故选:D.
【点评】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
2.(3分)下列各组数中,不是勾股数的是( )
A.3,4,5 B.5,12,13 C.7,25,26 D.6,8,10
【考点】勾股数.
【解答】解:A、32+42=52,能构成直角三角形,是整数,故是勾股数,此选项不符合题意;
B、52+122=132,是正整数,同时能构成直角三角形,故是勾股数,此选项不符合题意;
C、72+252≠262,不是勾股数,此选项符合题意;
D、62+82=102,三边是整数,同时能构成直角三角形,故是勾股数,此选项不符合题意.
故选:C.
【点评】此题主要考查了勾股数,解答此题要用到勾股数的定义,及勾股定理的逆定理:已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.
3.(3分)如图,三角形ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD的长为( )
A.1 B.2 C.2.5 D.3
【考点】含30度角的直角三角形.
【解答】解:∵∠ACB=90°,∠A=30°,AB=8,
∴BC=AB=4,∠B=60°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠BCD=30°,
∴BD=BC=2,
故选:B.
【点评】本题考查了含30°角的直角三角形的性质,熟练掌握这个性质是解题的关键.
4.(3分)下列命题是真命题的是( )
A.对角线相等的平行四边形是菱形
B.有一组邻边相等的平行四边形是菱形
C.对角线相互垂直且相等的四边形是菱形
D.有一组对边平行且相等的四边形是菱形
【考点】命题与定理.
【解答】解:A、对角线相等的平行四边形是矩形,故错误,不符合题意;
B、有一组邻边相等的平行四边形是菱形,正确,符合题意;
C、对角线互相垂直平分的四边是四菱形,故错误,不符合题意;
D、有一组对边平行且相等的四边形是平行四边形,故错误,不符合题意;
故选:B.
【点评】考查了菱形的判定,解题的关键是了解特殊的四边形的判定方法,难度不大.
5.(3分)如图,△ABC的三边AB,BC,CA的长分别为20,30,40,O是△ABC三条角平分线的交点,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
【考点】角平分线的性质.
【解答】解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,
∵点O是内心,
∴OE=OF=OD,
∴S△ABO:S△BCO:S△CAO= AB OE: BC OF: AC OD=AB:BC:AC=2:3:4,
故选:C.
【点评】本题主要考查了角平分线性质,三角形的面积公式,熟练掌握角平分线的性质是解题的关键.
6.(3分)公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是( )
A.4 B.6 C.8 D.16
【考点】勾股定理的证明;数学常识.
【解答】解:∵勾a=6,弦c=10,
∴股b==8,
∴小正方形的边长=8﹣6=2,
∴小正方形的面积=22=4
故选:A.
【点评】本题运用了勾股定理和正方形的面积公式,关键是运用了数形结合的数学思想.
7.(3分)下列各曲线表示的y与x的关系中,y是x的函数的是( )
A. B.
C. D.
【考点】函数的概念.
【解答】解:∵选项A,C,D中对于自变量x取值范围内的很多值,都有两个y的值与其对应,
故不符合题意;
∵选项B中每个自变量x,都有唯一的函数值与其对应,
∴选项B符合题意,
故选:B.
【点评】此题考查了利用图象理解函数概念的能力,关键是能准确理解函数的概念和能数形结合解决相关问题.
8.(3分)已知一次函数y=ax﹣1(a≠0)的函数值y随x值的增大而增大,则一次函数y=﹣ax+2(a≠0)的图象大致是( )
A. B.
C. D.
【考点】一次函数的性质;一次函数的图象.
【解答】解:∵一次函数y=ax﹣1(a≠0)的函数值y随x的增大而增大,
∴a>0,
∴﹣a<0,
∴函数y=﹣ax+2的图象经过第一、二、四象限,
故选:C.
【点评】本题考查一次函数的性质、一次函数的图象,解答本题的关键是明确题意,利用一次函数的性质解答.
9.(3分)在平面直角坐标系内,一次函数y=ax+b的图象如图所示,那么下列说法正确的是( )
A.当x>0时,﹣2<y<0
B.方程ax+b=0的解是x=﹣2
C.当y>﹣2时,x>0
D.不等式ax+b≤0的解集是x≤0
【考点】一次函数与一元一次不等式;一次函数的性质;一次函数与一元一次方程.
【解答】解:由函数y=ax+b的图象可知,
A、当x>0时,y>﹣2,原说法错误,不符合题意;
B、方程ax+b=0的解是x=1,原说法错误,不符合题意;
C、当y>﹣2时,x>0,正确,符合题意;
D、不等式ax+b≤0的解集是x≤1,原说法错误,不符合题意.
故选:C.
【点评】本题考查的是一次函数与一元一次不等式,一次函数的性质及一次函数与一元一次方程,利用数形结合求解是解答此题的关键.
10.(3分)如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )
A.1 B. C. D.
【考点】菱形的性质.
【解答】解:连接DB,作DH⊥AB于H,如图,
∵四边形ABCD为菱形,
∴AD=AB=BC=CD,
而∠A=60°,
∴△ABD和△BCD都是等边三角形,
∴∠ADB=∠DBC=60°,AD=BD,
在Rt△ADH中,AH=1,AD=2,
∴DH=,
在△ADE和△BDF中
,
∴△ADE≌△BDF,
∴∠2=∠1,DE=DF
∴∠1+∠BDE=∠2+∠BDE=∠ADB=60°,
∴△DEF为等边三角形,
∴EF=DE,
而当E点运动到H点时,DE的值最小,其最小值为,
∴EF的最小值为.
故选:D.
【点评】本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了等边三角形的判定与性质.
二.填空题(共7小题)
11.(3分)如果一个多边形的内角和为1260°,那么这个多边形是 九 边形.
【考点】多边形内角与外角.
【解答】解:设它的边数为n,根据题意,得(n﹣2) 180°=1260°,
所以n=9.
所以这是一个九边形.
故答案为:九.
【点评】本题考查多边形内角和与外角,掌握多边形的内角和公式结合方程是解决问题的关键.
12.(3分)如图,在△ABC中,∠ABC=90°,BD是△ABC的中线,DE⊥BC于点E.若BE=3,DE=4,则四边形ABED的面积为 18 .
【考点】三角形中位线定理;三角形的面积;直角三角形斜边上的中线.
【解答】解:∵∠ABC=90°,BD是△ABC的中线,
∴BD=CD=AC,
∵DE⊥BC,
∴BE=EC=3,
∴BC=2BE=6,
∴DE是△ABC的中位线,
∴AB=2DE=8,
∴四边形ABED的面积=△ABC的面积﹣△DEC的面积
=AB BC﹣DE EC
=×8×6﹣×4×3
=24﹣6
=18,
故答案为:18.
【点评】本题考查了三角形的中位线定理,直角三角形斜边上的中线,三角形的面积,熟练掌握三角形的中位线定理,以及直角三角形斜边上的中线性质是解题的关键.
13.(3分)已知一次函数y=mx+n与x轴的交点为(﹣5,0),则方程mx+n=0的解是 x=﹣5 .
【考点】一次函数与一元一次方程;一次函数的性质.
【解答】解:∵一次函数y=mx+n与x轴的交点为(﹣5,0),
∴方程mx+n=0的解是x=﹣5,
故答案为:x=﹣5.
【点评】本题考查了一次函数与一元一次方程的关系,熟练掌握一次函数图象上点的坐标特征是解题的关键.
14.(3分)已知P1(﹣1,y1),P2(﹣2,y2)在函数y=2x+b的图象上,则y1 > y2.(填写>,<或者=)
【考点】一次函数图象上点的坐标特征.
【解答】解:∵一次函数y=2x+b中k=2>0,
∴函数y=2x+b的函数值是y随x的增大而增大,
∵﹣1>﹣2,
∴y1>y2.
故答案为:>.
【点评】本题开查的是一次函数图象上点的坐标特点及一次函数的性质,熟知一次函数的增减性是解答此题的关键.
15.(3分)如图,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,则x的取值范围为 x≤1. .
【考点】一次函数与一元一次不等式;一次函数的性质.
【解答】解:由题意,将P(1,1)代入y=kx+b(k<0),
可得k+b=1,即k﹣1=﹣b,
整理kx+b≥x得,(k﹣1)x+b≥0,
∴﹣bx+b≥0,
由图象可知b>0,
∴x﹣1≤0,
∴x≤1,
故答案为:x≤1.
【点评】本题考查了一次函数的图象和性质,解题关键在于灵活应用待定系数法和不等式的性质.
16.(3分)甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶,乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h; ②m=160; ③点H的坐标是(7,85);④n=7.4,其中正确的有 ①②④ (填序号).
【考点】一次函数的应用.
【解答】解:由图象可知,乙出发时,甲乙相距80km,2小时后,乙车追上甲.则说明乙每小时比甲快40km,
∴乙的速度为120km/h.
故①正确;
由图象第2﹣6小时,乙由相遇点到达B,用时4小时,每小时比甲快40km,
则此时甲乙距离4×40=160km,则m=160,
故②正确;
当乙在B休息1h时,甲前进80km,则H点坐标为(7,80),
故③错误;
乙返回时,甲乙相距80km,到两车相遇用时80÷(120+80)=0.4小时,
则n=6+1+0.4=7.4,
故④正确.
故答案为:①②④.
【点评】本题考查一次函数的应用,主要是以函数图象为背景,考查双动点条件下,两点距离与运动时间的函数关系,解答时既要注意图象变化趋势,又要关注动点的运动状态.
三.解答题(共10小题)
17.(6分)在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)将△ABC先向右平移4个单位,再向上平移2个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标;
(2)画出△A1B1C1关于x轴对称的△A2B2C2,并写出点C2的坐标.
【考点】作图﹣轴对称变换;作图﹣平移变换.
【解答】解:(1)如图,△A1B1C1为所作,B1(2,﹣2);
(2)如图,△A2B2C2为所作,点C2的坐标为(3,0).
【点评】本题考查了作图﹣轴对称变换:几何图形都可看作是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的.也考查了平移变换.
18.(6分)如图,这是某校的平面示意图,如以正东为x轴正方向,正北为y轴正方向建立平面直角坐标系后,得到初中楼的坐标是(﹣4,2),实验楼的坐标是(﹣4,0).
(1)坐标原点应为 高中楼 的位置;
(2)在图中画出此平面直角坐标系;
(3)校门在第 四 象限:图书馆的坐标是 (4,1) ;分布在第二象限的是 初中楼 .
【考点】坐标确定位置.
【解答】解:(1)由题意得,可以建立如下坐标系,
∴坐标原点应为高中楼的位置,
故答案为:高中楼;
(2)如图所示,该平面直角坐标系即为所求;
(3)由坐标系可知,校门在第四象限,图书馆的坐标为(4,1),分布在第一象限的是,图书馆和操场,
故答案为:四,(4,1),初中楼.
【点评】本题主要考查了实际问题中用坐标表示位置,正确找到原点是解题的关键.
19.(6分)如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.
(1)求证:△ABC≌△DEF;
(2)若∠A=65°,求∠AGF的度数.
【考点】全等三角形的判定与性质.
【解答】(1)证明:∵AB⊥BE,
∴∠B=90°,
∵DE⊥BE,
∴∠E=90°,
∵BF=CE,
∴BF+CF=CE+CF,
即CB=EF,
在Rt△ABC和Rt△DEF中,,
∴Rt△ABC≌Rt△DEF(HL)
(2)解:∵∠A=65°,AB⊥BE,
∴∠ACB=90°﹣65°=25°,
由(1)知Rt△ABC≌Rt△DEF,
∴∠ACB=∠DFE=25°,
∴∠AGF=∠ACB+∠DFE=50°
【点评】本题考查了全等三角形的判定与性质、直角三角形的性质以及三角形的外角性质;证明三角形全等是解题的关键.
20.(8分)如图,在四边形ABCD中,∠BAC=∠ACD=90°,CD=2AB,E是CD的中点.
(1)求证:四边形ABCE是平行四边形;
(2)若AC=6,AD=10,求 ABCE的面积.
【考点】平行四边形的判定与性质;勾股定理.
【解答】(1)证明:∵∠BAC=∠ACD=90°,
∴AB∥CE,
∵点E是CD的中点,
∴CD=2CE,
∵CD=2AB,
∴AB=EC,
∴四边形ABCE是平行四边形;
(2)解:∵∠ACD=90°,AC=6,AD=10,
∴CD===8,
∵CD=2AB,
∴AB=4,
∴S平行四边形ABCE=AB AC=4×6=24.
【点评】本题考查了平行四边形的判定与性质,勾股定理等知识,证出四边形ABCE为平行四边形是解题的关键.
21.(8分)如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,并且DE⊥AB,若AB=4,求:
(1)∠ABC的度数;
(2)对角线AC的长;
(3)菱形ABCD的面积.
【考点】菱形的性质.
【解答】解:(1)∵E为AB的中点,且DE⊥AB,
∴AD=BD,
∵四边形ABCD是菱形,
∴AD=AB,
∴AD=AB=BD,
∴△ABD是等边三角形,
∴∠DAB=60°,
∴∠ABC=120°;
(2)∵AB=4,
∴AD=AB=4,AE=AB=2,
∴DE==2,
∵△ABD是等边三角形,AO⊥BD,DE⊥AB,
∴AO=DE=2,
∴AC=4;
(3)S菱形ABCD=AB DE=4×2=8.
【点评】此题考查了菱形的性质、等边三角形的判定与性质、线段垂直平分线的性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.
22.(9分)已知一次函数y=(1﹣2m)x+m+1;
(1)若一次函数图象经过点P(2,0),求m的值;
(2)若一次函数的图象经过第一、二、三象限;
①求m的取值范围;
②若点M(a﹣1,y1),N(a,y2),在该一次函数的图象上,比较y1和y2大小.
【考点】一次函数图象与系数的关系;一次函数图象上点的坐标特征.
【解答】解:(1)∵一次函数y=(1﹣2m)x+m+1的图象经过点P(2,0),
∴0=(1﹣2m)×2+m+1,
解得,m=1,
即m的值是1;
(2)①∵一次函数y=(1﹣2m)x+m+1的图象经过第一、二、三象限,
∴,
解得,﹣1<m<;
②∵一次函数y=(1﹣2m)x+m+1的图象经过第一、二、三象限,
∴1﹣2m>0,
∴该函数y随x的增大而增大,
∵点M(a﹣1,y1),N(a,y2)在该一次函数的图象上,a﹣1<a,
∴y1<y2.
【点评】本题考查一次函数图象与系数的关系,一次函数图象上点的坐标特征,一次函数的增减性,解答本题的关键是明确题意,利用一次函数的性质解答.
23.(9分)如图, ABCD的对角线AC,BD交于点O,过点D作DE⊥BC于E,延长CB到点F,使BF=CE,连接AF,OF.
(1)求证:四边形AFED是矩形.
(2)若AD=7,BE=2,∠ABF=45°,试求OF的长.
【考点】矩形的判定与性质;平行四边形的性质.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵BF=CE,
∴FE=BC,
∴四边形AFED是平行四边形,
∵DE⊥BC,
∴∠DEF=90°,
∴四边形AFED是矩形.
(2)解:由(1)得:∠AFE=90°,FE=AD,
∵AD=7,BE=2,
∴FE=7,
∴FB=FE﹣BE=5,
∴CE=BF=5,
∴FC=FE+CE=7+5=12,
∵∠ABF=45°,
∴△ABF是等腰直角三角形,
∴AF=FB=5,
在Rt△AFC中,由勾股定理得:AC===13,
∵四边形ABCD是平行四边形,
∴OA=OC,
∴OF=AC=.
【点评】本题考查了矩形的判定和性质,平行四边形的判定与性质,勾股定理以及直角三角形斜边上的中线性质等知识;正确的识别图形是解题的关键.
24.(10分)受新冠肺炎疫情影响,一水果种植专业户有大量成熟水果无法出售.“一方有难,八方支援”.某水果经销商主动从该种植专业户购进甲、乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按25元/千克的价格出售.设经销商购进甲种水果x千克,付款y元,y与x之间的函数关系如图所示.
(1)求出当0≤x≤50和x>50时,y与x之间的函数关系式;
(2)若经销商计划一次性购进甲、乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲、乙两种水果的购进量,才能使经销商付款总金额w(元)最少?
【考点】一次函数的应用;一元一次不等式的应用.
【解答】解:(1)当0≤x≤50时,设y=k1x(k1≠0),根据题意得50k1=1500,
解得k1=30;
∴y=30x;
当x>50时,设y=k2x+b(k2≠0),
根据题意得,,
解得,
∴y=24x+300.
∴y=;
(2)购进甲种水果为x千克,则购进乙种水果(100﹣x)千克,
∴40≤x≤60,
当40≤x≤50时,w1=30x+25(100﹣x)=5x+2500.
当x=40 时.wmin=2700 元,
当50<x≤60时,w2=24x+300+25(100﹣x)=﹣x+2800.
当x=60时,wmin=2740 元,
∵2740>2700,
∴当x=40时,总费用最少,最少总费用为2700 元.
此时乙种水果100﹣40=60(千克).
答:购进甲种水果为40千克,购进乙种水果60千克,才能使经销商付款总金额w(元)最少.
【点评】本题主要考查了一次函数的图象以及一元一次不等式组的应用.借助函数图象表达题目中的信息,读懂图象是关键.
25.(10分)如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)求k、b和m的值;
(2)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由;
(3)若动点P在线段DA上从点D开始以每秒1个单位的速度向点A运动,设点P的运动时间为t秒.是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
【考点】一次函数综合题.
【解答】解:(1)∵直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),
∴5=1+b,
∴b=4,
∴直线l2:y=﹣x+4,
∵直线l2:y=﹣x+4经过点C(2,m),
∴m=﹣2+4=2,
∴C(2,2),
把C(2,2)代入y=kx+1,得到k=.
∴k=,b=4,m=2.
(2)作点C关于x轴的对称点C′,连接BC′交x轴于E,连接EC,则△BCE的周长最小.
∵B(﹣1,5),C′(2,﹣2),
∴直线BC′的解析式为y=﹣x+,
令y=0,得到x=,
∴E(,0).
(3)如图,由题意AC==2,
当AC=AP=2时,t=6﹣2,
当P′C=P′A时,∠AP′C=90°,AP′=2,
∴t=6﹣2=4,
当AC=CP时,P(0,0),此时t=2.
综上所述,满足条件的t的值为6﹣2或4或2.
【点评】本题属于一次函数综合题,考查了一次函数的性质,待定系数法,轴对称最短问题,等腰三角形的判定和性质,三角形的面积等知识,解题的关键是学会利用轴对称解决最短问题,学会用分类讨论的思想思考问题,属于中考压轴题.
一.选择题(共12小题)
1.(3分)下列食品标识中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.(3分)下列各组数中,不是勾股数的是( )
A.3,4,5 B.5,12,13 C.7,25,26 D.6,8,10
3.(3分)如图,三角形ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD的长为( )
A.1 B.2 C.2.5 D.3
4.(3分)下列命题是真命题的是( )
A.对角线相等的平行四边形是菱形
B.有一组邻边相等的平行四边形是菱形
C.对角线相互垂直且相等的四边形是菱形
D.有一组对边平行且相等的四边形是菱形
5.(3分)如图,△ABC的三边AB,BC,CA的长分别为20,30,40,O是△ABC三条角平分线的交点,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
6.(3分)公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是( )
A.4 B.6 C.8 D.16
7.(3分)下列各曲线表示的y与x的关系中,y是x的函数的是( )
A. B.
C. D.
8.(3分)已知一次函数y=ax﹣1(a≠0)的函数值y随x值的增大而增大,则一次函数y=﹣ax+2(a≠0)的图象大致是( )
A. B.
C. D.
9.(3分)在平面直角坐标系内,一次函数y=ax+b的图象如图所示,那么下列说法正确的是( )
A.当x>0时,﹣2<y<0
B.方程ax+b=0的解是x=﹣2
C.当y>﹣2时,x>0
D.不等式ax+b≤0的解集是x≤0
10.(3分)如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )
A.1 B. C. D.
二.填空题(共7小题)
11.(3分)如果一个多边形的内角和为1260°,那么这个多边形是 边形.
12.(3分)如图,在△ABC中,∠ABC=90°,BD是△ABC的中线,DE⊥BC于点E.若BE=3,DE=4,则四边形ABED的面积为 .
13.(3分)已知一次函数y=mx+n与x轴的交点为(﹣5,0),则方程mx+n=0的解是 .
14.(3分)已知P1(﹣1,y1),P2(﹣2,y2)在函数y=2x+b的图象上,则y1 y2.(填写>,<或者=)
15.(3分)如图,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,则x的取值范围为 .
16.(3分)甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶,乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h; ②m=160; ③点H的坐标是(7,85);④n=7.4,其中正确的有 (填序号).
三.解答题(共10小题)
17.(6分)在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)将△ABC先向右平移4个单位,再向上平移2个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标;
(2)画出△A1B1C1关于x轴对称的△A2B2C2,并写出点C2的坐标.
18.(6分)如图,这是某校的平面示意图,如以正东为x轴正方向,正北为y轴正方向建立平面直角坐标系后,得到初中楼的坐标是(﹣4,2),实验楼的坐标是(﹣4,0).
(1)坐标原点应为 的位置;
(2)在图中画出此平面直角坐标系;
(3)校门在第 象限:图书馆的坐标是 ;分布在第二象限的是 .
19.(6分)如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.
(1)求证:△ABC≌△DEF;
(2)若∠A=65°,求∠AGF的度数.
20.(8分)如图,在四边形ABCD中,∠BAC=∠ACD=90°,CD=2AB,E是CD的中点.
(1)求证:四边形ABCE是平行四边形;
(2)若AC=6,AD=10,求 ABCE的面积.
21.(8分)如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,并且DE⊥AB,若AB=4,求:
(1)∠ABC的度数;
(2)对角线AC的长;
(3)菱形ABCD的面积.
22.(9分)已知一次函数y=(1﹣2m)x+m+1;
(1)若一次函数图象经过点P(2,0),求m的值;
(2)若一次函数的图象经过第一、二、三象限;
①求m的取值范围;
②若点M(a﹣1,y1),N(a,y2),在该一次函数的图象上,比较y1和y2大小.
23.(9分)如图, ABCD的对角线AC,BD交于点O,过点D作DE⊥BC于E,延长CB到点F,使BF=CE,连接AF,OF.
(1)求证:四边形AFED是矩形.
(2)若AD=7,BE=2,∠ABF=45°,试求OF的长.
24.(10分)受新冠肺炎疫情影响,一水果种植专业户有大量成熟水果无法出售.“一方有难,八方支援”.某水果经销商主动从该种植专业户购进甲、乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按25元/千克的价格出售.设经销商购进甲种水果x千克,付款y元,y与x之间的函数关系如图所示.
(1)求出当0≤x≤50和x>50时,y与x之间的函数关系式;
(2)若经销商计划一次性购进甲、乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲、乙两种水果的购进量,才能使经销商付款总金额w(元)最少?
25.(10分)如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)求k、b和m的值;
(2)求△ADC的面积;
(3)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由;
(4)若动点P在线段DA上从点D开始以每秒1个单位的速度向点A运动,设点P的运动时间为t秒.是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
第三次课后服务练习(范围:1—4单元)
参考答案与试题解析
一.选择题(共12小题)
1.(3分)下列食品标识中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【考点】中心对称图形;轴对称图形.
【解答】解:A.不是轴对称图形,也不是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.不是轴对称图形,是中心对称图形,故此选项不合题意;
D.既是轴对称图形又是中心对称图形,故此选项符合题意.
故选:D.
【点评】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
2.(3分)下列各组数中,不是勾股数的是( )
A.3,4,5 B.5,12,13 C.7,25,26 D.6,8,10
【考点】勾股数.
【解答】解:A、32+42=52,能构成直角三角形,是整数,故是勾股数,此选项不符合题意;
B、52+122=132,是正整数,同时能构成直角三角形,故是勾股数,此选项不符合题意;
C、72+252≠262,不是勾股数,此选项符合题意;
D、62+82=102,三边是整数,同时能构成直角三角形,故是勾股数,此选项不符合题意.
故选:C.
【点评】此题主要考查了勾股数,解答此题要用到勾股数的定义,及勾股定理的逆定理:已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.
3.(3分)如图,三角形ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,则BD的长为( )
A.1 B.2 C.2.5 D.3
【考点】含30度角的直角三角形.
【解答】解:∵∠ACB=90°,∠A=30°,AB=8,
∴BC=AB=4,∠B=60°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠BCD=30°,
∴BD=BC=2,
故选:B.
【点评】本题考查了含30°角的直角三角形的性质,熟练掌握这个性质是解题的关键.
4.(3分)下列命题是真命题的是( )
A.对角线相等的平行四边形是菱形
B.有一组邻边相等的平行四边形是菱形
C.对角线相互垂直且相等的四边形是菱形
D.有一组对边平行且相等的四边形是菱形
【考点】命题与定理.
【解答】解:A、对角线相等的平行四边形是矩形,故错误,不符合题意;
B、有一组邻边相等的平行四边形是菱形,正确,符合题意;
C、对角线互相垂直平分的四边是四菱形,故错误,不符合题意;
D、有一组对边平行且相等的四边形是平行四边形,故错误,不符合题意;
故选:B.
【点评】考查了菱形的判定,解题的关键是了解特殊的四边形的判定方法,难度不大.
5.(3分)如图,△ABC的三边AB,BC,CA的长分别为20,30,40,O是△ABC三条角平分线的交点,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
【考点】角平分线的性质.
【解答】解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,
∵点O是内心,
∴OE=OF=OD,
∴S△ABO:S△BCO:S△CAO= AB OE: BC OF: AC OD=AB:BC:AC=2:3:4,
故选:C.
【点评】本题主要考查了角平分线性质,三角形的面积公式,熟练掌握角平分线的性质是解题的关键.
6.(3分)公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是( )
A.4 B.6 C.8 D.16
【考点】勾股定理的证明;数学常识.
【解答】解:∵勾a=6,弦c=10,
∴股b==8,
∴小正方形的边长=8﹣6=2,
∴小正方形的面积=22=4
故选:A.
【点评】本题运用了勾股定理和正方形的面积公式,关键是运用了数形结合的数学思想.
7.(3分)下列各曲线表示的y与x的关系中,y是x的函数的是( )
A. B.
C. D.
【考点】函数的概念.
【解答】解:∵选项A,C,D中对于自变量x取值范围内的很多值,都有两个y的值与其对应,
故不符合题意;
∵选项B中每个自变量x,都有唯一的函数值与其对应,
∴选项B符合题意,
故选:B.
【点评】此题考查了利用图象理解函数概念的能力,关键是能准确理解函数的概念和能数形结合解决相关问题.
8.(3分)已知一次函数y=ax﹣1(a≠0)的函数值y随x值的增大而增大,则一次函数y=﹣ax+2(a≠0)的图象大致是( )
A. B.
C. D.
【考点】一次函数的性质;一次函数的图象.
【解答】解:∵一次函数y=ax﹣1(a≠0)的函数值y随x的增大而增大,
∴a>0,
∴﹣a<0,
∴函数y=﹣ax+2的图象经过第一、二、四象限,
故选:C.
【点评】本题考查一次函数的性质、一次函数的图象,解答本题的关键是明确题意,利用一次函数的性质解答.
9.(3分)在平面直角坐标系内,一次函数y=ax+b的图象如图所示,那么下列说法正确的是( )
A.当x>0时,﹣2<y<0
B.方程ax+b=0的解是x=﹣2
C.当y>﹣2时,x>0
D.不等式ax+b≤0的解集是x≤0
【考点】一次函数与一元一次不等式;一次函数的性质;一次函数与一元一次方程.
【解答】解:由函数y=ax+b的图象可知,
A、当x>0时,y>﹣2,原说法错误,不符合题意;
B、方程ax+b=0的解是x=1,原说法错误,不符合题意;
C、当y>﹣2时,x>0,正确,符合题意;
D、不等式ax+b≤0的解集是x≤1,原说法错误,不符合题意.
故选:C.
【点评】本题考查的是一次函数与一元一次不等式,一次函数的性质及一次函数与一元一次方程,利用数形结合求解是解答此题的关键.
10.(3分)如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )
A.1 B. C. D.
【考点】菱形的性质.
【解答】解:连接DB,作DH⊥AB于H,如图,
∵四边形ABCD为菱形,
∴AD=AB=BC=CD,
而∠A=60°,
∴△ABD和△BCD都是等边三角形,
∴∠ADB=∠DBC=60°,AD=BD,
在Rt△ADH中,AH=1,AD=2,
∴DH=,
在△ADE和△BDF中
,
∴△ADE≌△BDF,
∴∠2=∠1,DE=DF
∴∠1+∠BDE=∠2+∠BDE=∠ADB=60°,
∴△DEF为等边三角形,
∴EF=DE,
而当E点运动到H点时,DE的值最小,其最小值为,
∴EF的最小值为.
故选:D.
【点评】本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了等边三角形的判定与性质.
二.填空题(共7小题)
11.(3分)如果一个多边形的内角和为1260°,那么这个多边形是 九 边形.
【考点】多边形内角与外角.
【解答】解:设它的边数为n,根据题意,得(n﹣2) 180°=1260°,
所以n=9.
所以这是一个九边形.
故答案为:九.
【点评】本题考查多边形内角和与外角,掌握多边形的内角和公式结合方程是解决问题的关键.
12.(3分)如图,在△ABC中,∠ABC=90°,BD是△ABC的中线,DE⊥BC于点E.若BE=3,DE=4,则四边形ABED的面积为 18 .
【考点】三角形中位线定理;三角形的面积;直角三角形斜边上的中线.
【解答】解:∵∠ABC=90°,BD是△ABC的中线,
∴BD=CD=AC,
∵DE⊥BC,
∴BE=EC=3,
∴BC=2BE=6,
∴DE是△ABC的中位线,
∴AB=2DE=8,
∴四边形ABED的面积=△ABC的面积﹣△DEC的面积
=AB BC﹣DE EC
=×8×6﹣×4×3
=24﹣6
=18,
故答案为:18.
【点评】本题考查了三角形的中位线定理,直角三角形斜边上的中线,三角形的面积,熟练掌握三角形的中位线定理,以及直角三角形斜边上的中线性质是解题的关键.
13.(3分)已知一次函数y=mx+n与x轴的交点为(﹣5,0),则方程mx+n=0的解是 x=﹣5 .
【考点】一次函数与一元一次方程;一次函数的性质.
【解答】解:∵一次函数y=mx+n与x轴的交点为(﹣5,0),
∴方程mx+n=0的解是x=﹣5,
故答案为:x=﹣5.
【点评】本题考查了一次函数与一元一次方程的关系,熟练掌握一次函数图象上点的坐标特征是解题的关键.
14.(3分)已知P1(﹣1,y1),P2(﹣2,y2)在函数y=2x+b的图象上,则y1 > y2.(填写>,<或者=)
【考点】一次函数图象上点的坐标特征.
【解答】解:∵一次函数y=2x+b中k=2>0,
∴函数y=2x+b的函数值是y随x的增大而增大,
∵﹣1>﹣2,
∴y1>y2.
故答案为:>.
【点评】本题开查的是一次函数图象上点的坐标特点及一次函数的性质,熟知一次函数的增减性是解答此题的关键.
15.(3分)如图,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,则x的取值范围为 x≤1. .
【考点】一次函数与一元一次不等式;一次函数的性质.
【解答】解:由题意,将P(1,1)代入y=kx+b(k<0),
可得k+b=1,即k﹣1=﹣b,
整理kx+b≥x得,(k﹣1)x+b≥0,
∴﹣bx+b≥0,
由图象可知b>0,
∴x﹣1≤0,
∴x≤1,
故答案为:x≤1.
【点评】本题考查了一次函数的图象和性质,解题关键在于灵活应用待定系数法和不等式的性质.
16.(3分)甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶,乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h; ②m=160; ③点H的坐标是(7,85);④n=7.4,其中正确的有 ①②④ (填序号).
【考点】一次函数的应用.
【解答】解:由图象可知,乙出发时,甲乙相距80km,2小时后,乙车追上甲.则说明乙每小时比甲快40km,
∴乙的速度为120km/h.
故①正确;
由图象第2﹣6小时,乙由相遇点到达B,用时4小时,每小时比甲快40km,
则此时甲乙距离4×40=160km,则m=160,
故②正确;
当乙在B休息1h时,甲前进80km,则H点坐标为(7,80),
故③错误;
乙返回时,甲乙相距80km,到两车相遇用时80÷(120+80)=0.4小时,
则n=6+1+0.4=7.4,
故④正确.
故答案为:①②④.
【点评】本题考查一次函数的应用,主要是以函数图象为背景,考查双动点条件下,两点距离与运动时间的函数关系,解答时既要注意图象变化趋势,又要关注动点的运动状态.
三.解答题(共10小题)
17.(6分)在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)将△ABC先向右平移4个单位,再向上平移2个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标;
(2)画出△A1B1C1关于x轴对称的△A2B2C2,并写出点C2的坐标.
【考点】作图﹣轴对称变换;作图﹣平移变换.
【解答】解:(1)如图,△A1B1C1为所作,B1(2,﹣2);
(2)如图,△A2B2C2为所作,点C2的坐标为(3,0).
【点评】本题考查了作图﹣轴对称变换:几何图形都可看作是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的.也考查了平移变换.
18.(6分)如图,这是某校的平面示意图,如以正东为x轴正方向,正北为y轴正方向建立平面直角坐标系后,得到初中楼的坐标是(﹣4,2),实验楼的坐标是(﹣4,0).
(1)坐标原点应为 高中楼 的位置;
(2)在图中画出此平面直角坐标系;
(3)校门在第 四 象限:图书馆的坐标是 (4,1) ;分布在第二象限的是 初中楼 .
【考点】坐标确定位置.
【解答】解:(1)由题意得,可以建立如下坐标系,
∴坐标原点应为高中楼的位置,
故答案为:高中楼;
(2)如图所示,该平面直角坐标系即为所求;
(3)由坐标系可知,校门在第四象限,图书馆的坐标为(4,1),分布在第一象限的是,图书馆和操场,
故答案为:四,(4,1),初中楼.
【点评】本题主要考查了实际问题中用坐标表示位置,正确找到原点是解题的关键.
19.(6分)如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.
(1)求证:△ABC≌△DEF;
(2)若∠A=65°,求∠AGF的度数.
【考点】全等三角形的判定与性质.
【解答】(1)证明:∵AB⊥BE,
∴∠B=90°,
∵DE⊥BE,
∴∠E=90°,
∵BF=CE,
∴BF+CF=CE+CF,
即CB=EF,
在Rt△ABC和Rt△DEF中,,
∴Rt△ABC≌Rt△DEF(HL)
(2)解:∵∠A=65°,AB⊥BE,
∴∠ACB=90°﹣65°=25°,
由(1)知Rt△ABC≌Rt△DEF,
∴∠ACB=∠DFE=25°,
∴∠AGF=∠ACB+∠DFE=50°
【点评】本题考查了全等三角形的判定与性质、直角三角形的性质以及三角形的外角性质;证明三角形全等是解题的关键.
20.(8分)如图,在四边形ABCD中,∠BAC=∠ACD=90°,CD=2AB,E是CD的中点.
(1)求证:四边形ABCE是平行四边形;
(2)若AC=6,AD=10,求 ABCE的面积.
【考点】平行四边形的判定与性质;勾股定理.
【解答】(1)证明:∵∠BAC=∠ACD=90°,
∴AB∥CE,
∵点E是CD的中点,
∴CD=2CE,
∵CD=2AB,
∴AB=EC,
∴四边形ABCE是平行四边形;
(2)解:∵∠ACD=90°,AC=6,AD=10,
∴CD===8,
∵CD=2AB,
∴AB=4,
∴S平行四边形ABCE=AB AC=4×6=24.
【点评】本题考查了平行四边形的判定与性质,勾股定理等知识,证出四边形ABCE为平行四边形是解题的关键.
21.(8分)如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,并且DE⊥AB,若AB=4,求:
(1)∠ABC的度数;
(2)对角线AC的长;
(3)菱形ABCD的面积.
【考点】菱形的性质.
【解答】解:(1)∵E为AB的中点,且DE⊥AB,
∴AD=BD,
∵四边形ABCD是菱形,
∴AD=AB,
∴AD=AB=BD,
∴△ABD是等边三角形,
∴∠DAB=60°,
∴∠ABC=120°;
(2)∵AB=4,
∴AD=AB=4,AE=AB=2,
∴DE==2,
∵△ABD是等边三角形,AO⊥BD,DE⊥AB,
∴AO=DE=2,
∴AC=4;
(3)S菱形ABCD=AB DE=4×2=8.
【点评】此题考查了菱形的性质、等边三角形的判定与性质、线段垂直平分线的性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.
22.(9分)已知一次函数y=(1﹣2m)x+m+1;
(1)若一次函数图象经过点P(2,0),求m的值;
(2)若一次函数的图象经过第一、二、三象限;
①求m的取值范围;
②若点M(a﹣1,y1),N(a,y2),在该一次函数的图象上,比较y1和y2大小.
【考点】一次函数图象与系数的关系;一次函数图象上点的坐标特征.
【解答】解:(1)∵一次函数y=(1﹣2m)x+m+1的图象经过点P(2,0),
∴0=(1﹣2m)×2+m+1,
解得,m=1,
即m的值是1;
(2)①∵一次函数y=(1﹣2m)x+m+1的图象经过第一、二、三象限,
∴,
解得,﹣1<m<;
②∵一次函数y=(1﹣2m)x+m+1的图象经过第一、二、三象限,
∴1﹣2m>0,
∴该函数y随x的增大而增大,
∵点M(a﹣1,y1),N(a,y2)在该一次函数的图象上,a﹣1<a,
∴y1<y2.
【点评】本题考查一次函数图象与系数的关系,一次函数图象上点的坐标特征,一次函数的增减性,解答本题的关键是明确题意,利用一次函数的性质解答.
23.(9分)如图, ABCD的对角线AC,BD交于点O,过点D作DE⊥BC于E,延长CB到点F,使BF=CE,连接AF,OF.
(1)求证:四边形AFED是矩形.
(2)若AD=7,BE=2,∠ABF=45°,试求OF的长.
【考点】矩形的判定与性质;平行四边形的性质.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵BF=CE,
∴FE=BC,
∴四边形AFED是平行四边形,
∵DE⊥BC,
∴∠DEF=90°,
∴四边形AFED是矩形.
(2)解:由(1)得:∠AFE=90°,FE=AD,
∵AD=7,BE=2,
∴FE=7,
∴FB=FE﹣BE=5,
∴CE=BF=5,
∴FC=FE+CE=7+5=12,
∵∠ABF=45°,
∴△ABF是等腰直角三角形,
∴AF=FB=5,
在Rt△AFC中,由勾股定理得:AC===13,
∵四边形ABCD是平行四边形,
∴OA=OC,
∴OF=AC=.
【点评】本题考查了矩形的判定和性质,平行四边形的判定与性质,勾股定理以及直角三角形斜边上的中线性质等知识;正确的识别图形是解题的关键.
24.(10分)受新冠肺炎疫情影响,一水果种植专业户有大量成熟水果无法出售.“一方有难,八方支援”.某水果经销商主动从该种植专业户购进甲、乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按25元/千克的价格出售.设经销商购进甲种水果x千克,付款y元,y与x之间的函数关系如图所示.
(1)求出当0≤x≤50和x>50时,y与x之间的函数关系式;
(2)若经销商计划一次性购进甲、乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲、乙两种水果的购进量,才能使经销商付款总金额w(元)最少?
【考点】一次函数的应用;一元一次不等式的应用.
【解答】解:(1)当0≤x≤50时,设y=k1x(k1≠0),根据题意得50k1=1500,
解得k1=30;
∴y=30x;
当x>50时,设y=k2x+b(k2≠0),
根据题意得,,
解得,
∴y=24x+300.
∴y=;
(2)购进甲种水果为x千克,则购进乙种水果(100﹣x)千克,
∴40≤x≤60,
当40≤x≤50时,w1=30x+25(100﹣x)=5x+2500.
当x=40 时.wmin=2700 元,
当50<x≤60时,w2=24x+300+25(100﹣x)=﹣x+2800.
当x=60时,wmin=2740 元,
∵2740>2700,
∴当x=40时,总费用最少,最少总费用为2700 元.
此时乙种水果100﹣40=60(千克).
答:购进甲种水果为40千克,购进乙种水果60千克,才能使经销商付款总金额w(元)最少.
【点评】本题主要考查了一次函数的图象以及一元一次不等式组的应用.借助函数图象表达题目中的信息,读懂图象是关键.
25.(10分)如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)求k、b和m的值;
(2)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由;
(3)若动点P在线段DA上从点D开始以每秒1个单位的速度向点A运动,设点P的运动时间为t秒.是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
【考点】一次函数综合题.
【解答】解:(1)∵直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),
∴5=1+b,
∴b=4,
∴直线l2:y=﹣x+4,
∵直线l2:y=﹣x+4经过点C(2,m),
∴m=﹣2+4=2,
∴C(2,2),
把C(2,2)代入y=kx+1,得到k=.
∴k=,b=4,m=2.
(2)作点C关于x轴的对称点C′,连接BC′交x轴于E,连接EC,则△BCE的周长最小.
∵B(﹣1,5),C′(2,﹣2),
∴直线BC′的解析式为y=﹣x+,
令y=0,得到x=,
∴E(,0).
(3)如图,由题意AC==2,
当AC=AP=2时,t=6﹣2,
当P′C=P′A时,∠AP′C=90°,AP′=2,
∴t=6﹣2=4,
当AC=CP时,P(0,0),此时t=2.
综上所述,满足条件的t的值为6﹣2或4或2.
【点评】本题属于一次函数综合题,考查了一次函数的性质,待定系数法,轴对称最短问题,等腰三角形的判定和性质,三角形的面积等知识,解题的关键是学会利用轴对称解决最短问题,学会用分类讨论的思想思考问题,属于中考压轴题.
同课章节目录
