青岛版数学七年级上册 1.4.2线段的作法课件(共13张PPT)
文档属性
| 名称 | 青岛版数学七年级上册 1.4.2线段的作法课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 455.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-09 17:44:34 | ||
图片预览



文档简介
(共13张PPT)
第1章 基本的几何图形
1.4 线段的比较与作法
第2课时 线段的作法
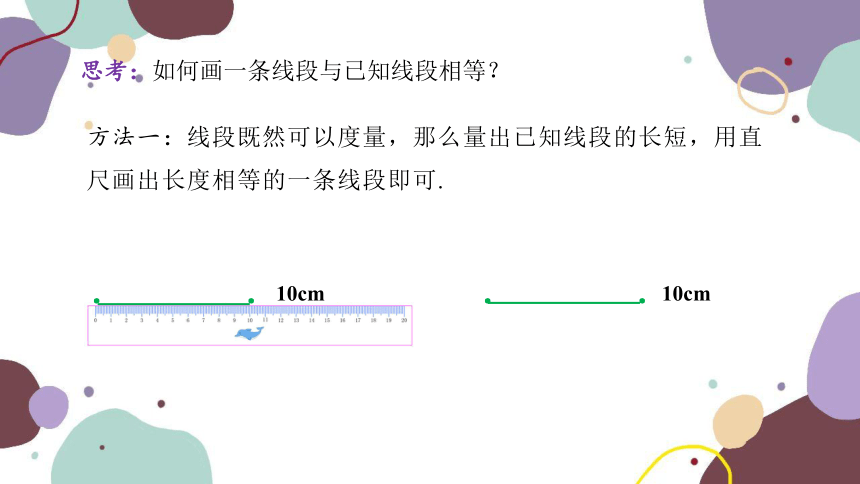
思考:如何画一条线段与已知线段相等?
方法一:线段既然可以度量,那么量出已知线段的长短,用直尺画出长度相等的一条线段即可.
·
·
10cm
·
·
10cm
方法二:不具体量出线段的长度值,直接复制线段.
·
·
①用圆规量取长度a
·
O
A
B
②用直尺画出射线OA,
这种作图方式就是尺规作图.
再用圆规在射线上截取OB=a.
思考:如何画一条线段与已知线段相等?
·
a
尺规作图:作线段的和.
再在AB的延长线上画线段BC=n.
A
M
已知:线段m、n(如图) ;
求作:线段AC,使AC=m + n.
作法:
(1)作直线AM;
B
C
则线段AC就是所求作的线段.
(2)在直线AM上画线段AB=m,
m
n
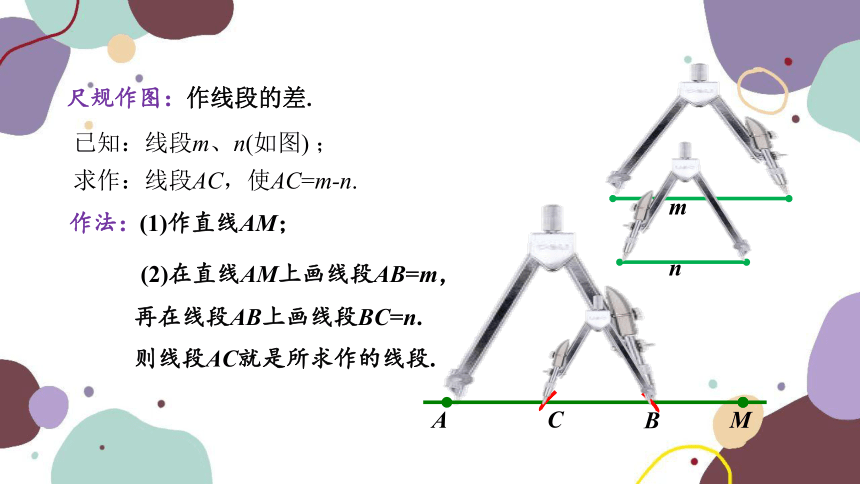
尺规作图:作线段的差.
再在线段AB上画线段BC=n.
A
M
已知:线段m、n(如图) ;
求作:线段AC,使AC=m-n.
作法:
(1)作直线AM;
B
C
则线段AC就是所求作的线段.
(2)在直线AM上画线段AB=m,
m
n
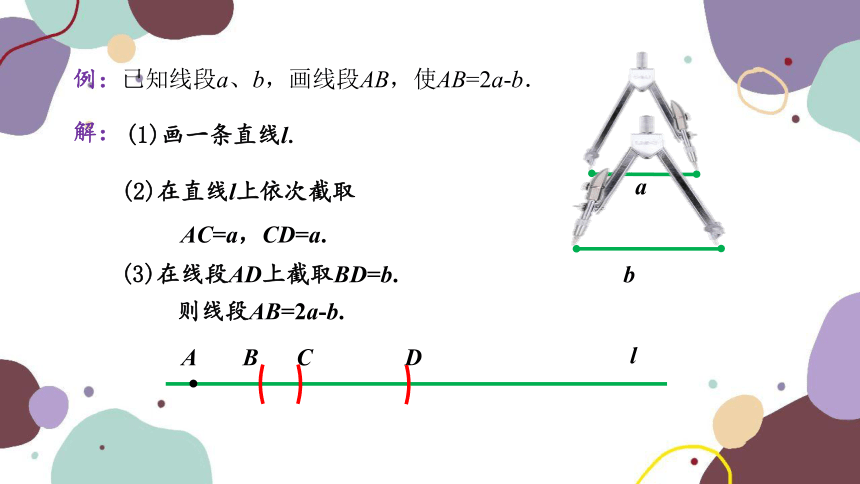
例:已知线段a、b,画线段AB,使AB=2a-b.
a
b
C
D
l
B
(2)在直线l上依次截取
AC=a,CD=a.
(3)在线段AD上截取BD=b.
则线段AB=2a-b.
解:
(1)画一条直线l.
A
思考:要把一根铅笔切成长度相等的两段,应该从何处切断?
A
B
M
如果点M把线段AB分成相等的两条线段AM与BM,那么点M叫做线段AB的中点.
定义:
D
A
B
P
A
A
B
B
P
P
注意:若点A是线段BC的中点,则AB=AC一定成立;
但反过来,若AB=AC,则点A不一定是线段BC的中点.
例:如图,C,D是线段AB上两点,且D是线段AC的中点,若AB=10厘米,BC=4厘米,则AD的长为( )
A.2厘米 B.3厘米 C.4厘米 D.6厘米
A D C B
B
拓展:线段的三等分点、四等分点.
将线段AB分成相等的三条线段AM,MN,NB,得到三等分点M,N.
A M N B
类似地,还可以得到四等分点等.
A M N P B
当堂检测
1.如图所示,点C,D为线段AB上两点,且CD=BD,则在下列说法中,正确的有( )
①AC<AD;②AC=AB-BC;③AD-AC=BD;④AD=AC+BD.
A.1个 B.2个 C.3个 D.4个
A C D B
D
2.已知线段a,b,用直尺和圆规作一条线段AB,使它的长度等于2a+b.
a
b
C
D
l
B
(2)在直线l上依次截取
AC=a,CD=a.
(3)在线段AD的延长线上作BD=b.
则线段AB=2a+b.
解:
(1)画一条直线l.
A
3.如图,D为线段CB的中点,AD=8厘米,AB=10厘米,求CB的长度.
A C D B
解:因为AD=8厘米,AB=10厘米,
所以DB=AB-AD=10-8=2厘米.
又因为D为线段CB的中点,
所以CB=2DB=2×2=4厘米.
第1章 基本的几何图形
1.4 线段的比较与作法
第2课时 线段的作法
思考:如何画一条线段与已知线段相等?
方法一:线段既然可以度量,那么量出已知线段的长短,用直尺画出长度相等的一条线段即可.
·
·
10cm
·
·
10cm
方法二:不具体量出线段的长度值,直接复制线段.
·
·
①用圆规量取长度a
·
O
A
B
②用直尺画出射线OA,
这种作图方式就是尺规作图.
再用圆规在射线上截取OB=a.
思考:如何画一条线段与已知线段相等?
·
a
尺规作图:作线段的和.
再在AB的延长线上画线段BC=n.
A
M
已知:线段m、n(如图) ;
求作:线段AC,使AC=m + n.
作法:
(1)作直线AM;
B
C
则线段AC就是所求作的线段.
(2)在直线AM上画线段AB=m,
m
n
尺规作图:作线段的差.
再在线段AB上画线段BC=n.
A
M
已知:线段m、n(如图) ;
求作:线段AC,使AC=m-n.
作法:
(1)作直线AM;
B
C
则线段AC就是所求作的线段.
(2)在直线AM上画线段AB=m,
m
n
例:已知线段a、b,画线段AB,使AB=2a-b.
a
b
C
D
l
B
(2)在直线l上依次截取
AC=a,CD=a.
(3)在线段AD上截取BD=b.
则线段AB=2a-b.
解:
(1)画一条直线l.
A
思考:要把一根铅笔切成长度相等的两段,应该从何处切断?
A
B
M
如果点M把线段AB分成相等的两条线段AM与BM,那么点M叫做线段AB的中点.
定义:
D
A
B
P
A
A
B
B
P
P
注意:若点A是线段BC的中点,则AB=AC一定成立;
但反过来,若AB=AC,则点A不一定是线段BC的中点.
例:如图,C,D是线段AB上两点,且D是线段AC的中点,若AB=10厘米,BC=4厘米,则AD的长为( )
A.2厘米 B.3厘米 C.4厘米 D.6厘米
A D C B
B
拓展:线段的三等分点、四等分点.
将线段AB分成相等的三条线段AM,MN,NB,得到三等分点M,N.
A M N B
类似地,还可以得到四等分点等.
A M N P B
当堂检测
1.如图所示,点C,D为线段AB上两点,且CD=BD,则在下列说法中,正确的有( )
①AC<AD;②AC=AB-BC;③AD-AC=BD;④AD=AC+BD.
A.1个 B.2个 C.3个 D.4个
A C D B
D
2.已知线段a,b,用直尺和圆规作一条线段AB,使它的长度等于2a+b.
a
b
C
D
l
B
(2)在直线l上依次截取
AC=a,CD=a.
(3)在线段AD的延长线上作BD=b.
则线段AB=2a+b.
解:
(1)画一条直线l.
A
3.如图,D为线段CB的中点,AD=8厘米,AB=10厘米,求CB的长度.
A C D B
解:因为AD=8厘米,AB=10厘米,
所以DB=AB-AD=10-8=2厘米.
又因为D为线段CB的中点,
所以CB=2DB=2×2=4厘米.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
