2023年广东省初中学业水平考试 数学模拟试卷(一)课件(共42张PPT)
文档属性
| 名称 | 2023年广东省初中学业水平考试 数学模拟试卷(一)课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-09 17:44:10 | ||
图片预览








文档简介
(共42张PPT)
第三部分 仿真模拟
2023年广东省初中学业水平考试
数学模拟试卷(一)
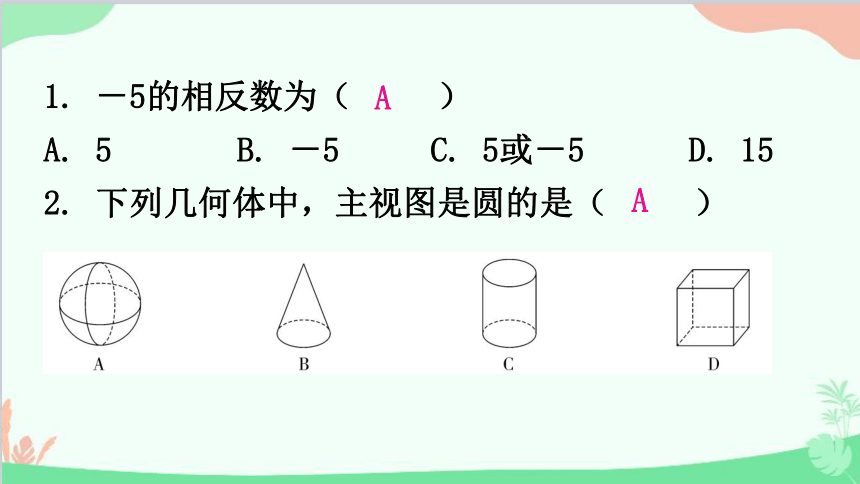
1. -5的相反数为( )
A. 5 B. -5 C. 5或-5 D. 15
2. 下列几何体中,主视图是圆的是( )
A
A
3. 习总书记指出,善于学习就是善于进步,“学习强国”平台上线后的某周末,全国大约有1.2亿人在平台上学习,1.2亿这个数用科学记数法表示,正确的是( )
A. 1.2×109 B. 1.2×108
C. 12×109 D. 1.2×1010
B
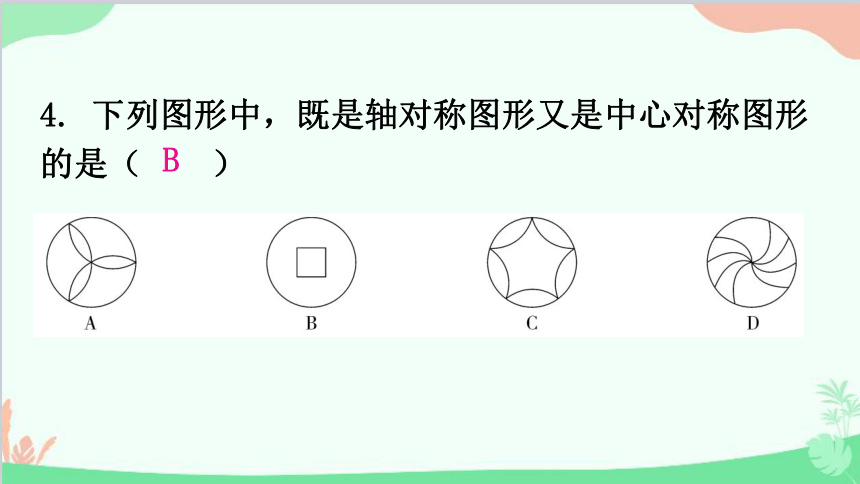
4. 下列图形中,既是轴对称图形又是中心对称图形的是( )
B
5. 下列计算正确的是( )
A. x2+x2=x4 B. (x2)3=x6
C. x6÷x2=x3 D. (xy2)3=xy6
B
C
C
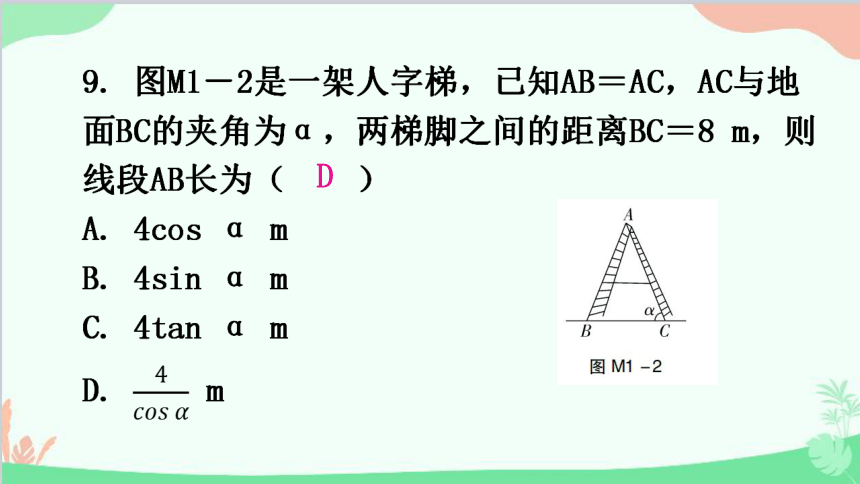
D
D
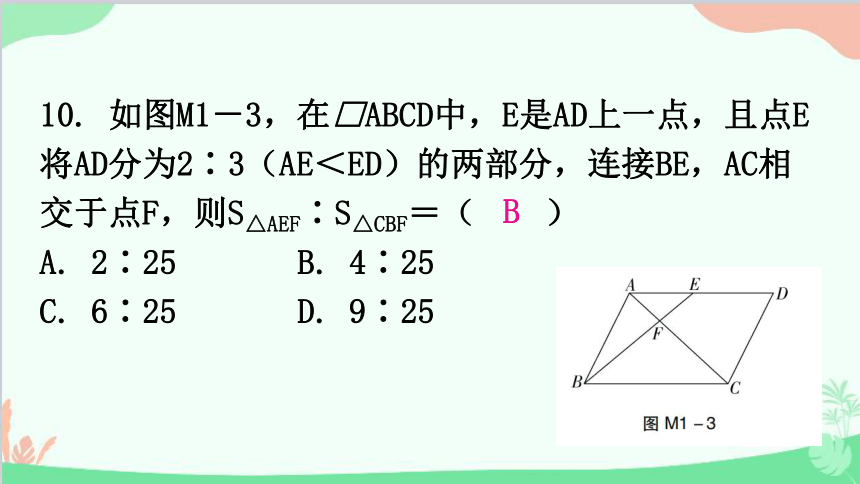
10. 如图M1-3,在□ABCD中,E是AD上一点,且点E将AD分为2∶3(AE<ED)的两部分,连接BE,AC相交于点F,则S△AEF∶S△CBF=( )
A. 2∶25 B. 4∶25
C. 6∶25 D. 9∶25
B
二、填空题(本大题5小题,每小题3分,共15分)请将下列各题的正确答案填写在答题卡相应的位置上.
11. 正十边形的外角和的度数为________.
12. 某三角形的周长为18 cm,它的三条中位线围成的三角形的周长是________cm.
360°
9
13. 一个不透明的袋中装有3个红球和2个白球,这些球除颜色外无其他差别. 现随机从袋中摸出一个
球,这个球是白球的概率是________.
14. 分解因式:a2+3a=________________.
a(a+3)
-6
18. 如图M1-5,在Rt△ABC中,∠C=90°,AC=8.
(1)尺规作图:作∠ABC的平分线交AC于点D;(不写作法,保留作图痕迹)
(2)若CD=3,求cos A.
解:(1)如答图M1-1,射线BD即为所作.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19. 近年来,校园安全受到全社会的广泛关注,为了了解学生对安全知识的掌握程度,学校采用随机抽样的调查方式,根据收集到的信息进行统计,绘制了如图M1-6所示的两幅不完整的统计图,请你根据统计图所提供的信息解答下列问题:
(1)接受问卷调查的学生共有________人,扇形统计图中“基本了解”部分所对应扇形的圆心角的度数为________;
(2)请补全条形统计图;
60
90°
(3)若该中学共有学生3 000人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
解:(2)60-15-30-10=5(人).
补全的条形统计图如答图M1-2.
20. 某厂计划生产A,B两种产品若干件,已知两种产品的成本价和销售价如下表:
类别 A种产品 B种产品
成本价/(元·件-1) 400 300
销售价/(元·件-1) 560 450
(1)工厂第一次用220 000元资金生产了A,B两种产品共600件,求两种产品各生产了多少件;
(2)工厂第二次生产时,工厂规定A种产品生产数量不得超过B种产品生产数量的一半. 工厂计划生产两种产品共3 000件,应如何设计生产方案才能获得最大利润,最大利润是多少?
(1)证明:∵将△ABC沿直线AB折叠得到△ABD,
∴BC=BD. ∴点B在CD的垂直平分线上.
同理,点A在CD的垂直平分线上.
∴AB⊥CD,即OA⊥CD.
∵AG∥CD,∴OA⊥GA.
∵OA是⊙O的半径,∴直线GA是⊙O的切线.
23. 如图M1-9,已知抛物线y=-x2+mx+n与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,3).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时点E的坐标.
谢 谢
第三部分 仿真模拟
2023年广东省初中学业水平考试
数学模拟试卷(一)
1. -5的相反数为( )
A. 5 B. -5 C. 5或-5 D. 15
2. 下列几何体中,主视图是圆的是( )
A
A
3. 习总书记指出,善于学习就是善于进步,“学习强国”平台上线后的某周末,全国大约有1.2亿人在平台上学习,1.2亿这个数用科学记数法表示,正确的是( )
A. 1.2×109 B. 1.2×108
C. 12×109 D. 1.2×1010
B
4. 下列图形中,既是轴对称图形又是中心对称图形的是( )
B
5. 下列计算正确的是( )
A. x2+x2=x4 B. (x2)3=x6
C. x6÷x2=x3 D. (xy2)3=xy6
B
C
C
D
D
10. 如图M1-3,在□ABCD中,E是AD上一点,且点E将AD分为2∶3(AE<ED)的两部分,连接BE,AC相交于点F,则S△AEF∶S△CBF=( )
A. 2∶25 B. 4∶25
C. 6∶25 D. 9∶25
B
二、填空题(本大题5小题,每小题3分,共15分)请将下列各题的正确答案填写在答题卡相应的位置上.
11. 正十边形的外角和的度数为________.
12. 某三角形的周长为18 cm,它的三条中位线围成的三角形的周长是________cm.
360°
9
13. 一个不透明的袋中装有3个红球和2个白球,这些球除颜色外无其他差别. 现随机从袋中摸出一个
球,这个球是白球的概率是________.
14. 分解因式:a2+3a=________________.
a(a+3)
-6
18. 如图M1-5,在Rt△ABC中,∠C=90°,AC=8.
(1)尺规作图:作∠ABC的平分线交AC于点D;(不写作法,保留作图痕迹)
(2)若CD=3,求cos A.
解:(1)如答图M1-1,射线BD即为所作.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19. 近年来,校园安全受到全社会的广泛关注,为了了解学生对安全知识的掌握程度,学校采用随机抽样的调查方式,根据收集到的信息进行统计,绘制了如图M1-6所示的两幅不完整的统计图,请你根据统计图所提供的信息解答下列问题:
(1)接受问卷调查的学生共有________人,扇形统计图中“基本了解”部分所对应扇形的圆心角的度数为________;
(2)请补全条形统计图;
60
90°
(3)若该中学共有学生3 000人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
解:(2)60-15-30-10=5(人).
补全的条形统计图如答图M1-2.
20. 某厂计划生产A,B两种产品若干件,已知两种产品的成本价和销售价如下表:
类别 A种产品 B种产品
成本价/(元·件-1) 400 300
销售价/(元·件-1) 560 450
(1)工厂第一次用220 000元资金生产了A,B两种产品共600件,求两种产品各生产了多少件;
(2)工厂第二次生产时,工厂规定A种产品生产数量不得超过B种产品生产数量的一半. 工厂计划生产两种产品共3 000件,应如何设计生产方案才能获得最大利润,最大利润是多少?
(1)证明:∵将△ABC沿直线AB折叠得到△ABD,
∴BC=BD. ∴点B在CD的垂直平分线上.
同理,点A在CD的垂直平分线上.
∴AB⊥CD,即OA⊥CD.
∵AG∥CD,∴OA⊥GA.
∵OA是⊙O的半径,∴直线GA是⊙O的切线.
23. 如图M1-9,已知抛物线y=-x2+mx+n与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,3).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时点E的坐标.
谢 谢
同课章节目录
