湘教版2022-2023学年度下学期七年级期末练习数学试5(含解析)
文档属性
| 名称 | 湘教版2022-2023学年度下学期七年级期末练习数学试5(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-08 14:04:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湘教版2022-2023学年度下学期七年级期末练习数学试5
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
在我市举办的中学生“争做文明盘锦人”演讲比赛中,有15名学生进入决赛,他们决赛的成绩各不相同,小明想知道自己能否进入前8名,不仅要了解自己的成绩,还要了解这15名学生成绩的( )
A.众数 B.方差 C.平均数 D.中位数
下列计算正确的是( )
A. a2+a2=a4 B. a2 a3=a6 C. a3÷a=a3 D. (a3)3=a9
若多项式因式分解后的一个因式是,则的值是( )
A. B. C. D.
如图,直线AB、CD相交于点O,OD平分∠BOE,则∠AOD的补角的个数为( )
A.1 个 B.2 个 C.3 个 D.4 个
正方形的对称轴的条数为( )
A.1 B.2 C.3 D.4
甲、乙、丙、丁四名同学在一次投掷实心球训练中,在相同条件下各投掷10次,他们成绩的平均数与方差s2如下表:
甲 乙 丙 丁
平均数(环) 11.1 11.1 10.9 10.9
方差s2 1.1 1.2 1.3 1.4
若要选一名成绩好且发挥稳定的同学参加比赛,则应该选择( )
A.甲 B.乙 C.丙 D.丁
端午节前夕,某超市用1680元购进A.B两种商品共60件,其中A型商品每件24元,B型商品每件36元.设购买A型商品x件、B型商品y件,依题意列方程组正确的是( )
A. B.C. D.
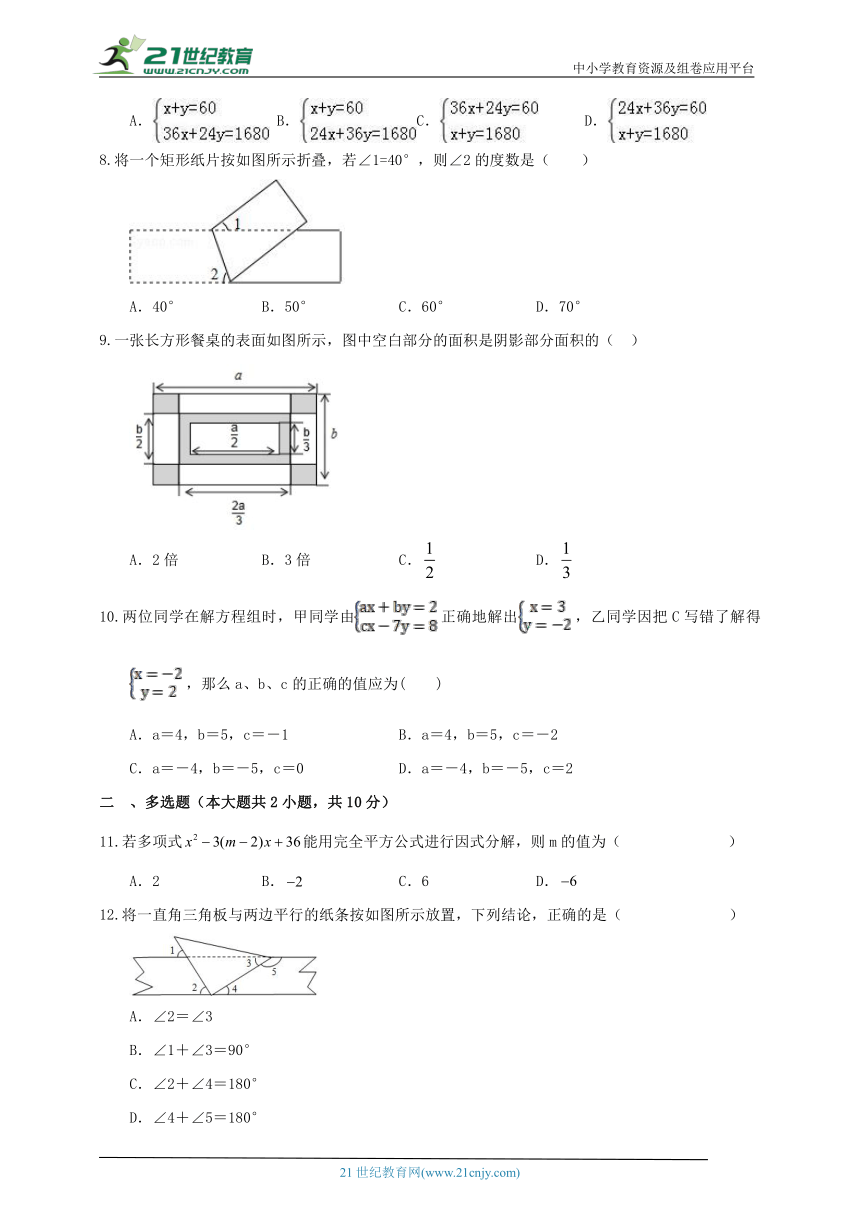
将一个矩形纸片按如图所示折叠,若∠1=40°,则∠2的度数是( )
A.40° B.50° C.60° D.70°
一张长方形餐桌的表面如图所示,图中空白部分的面积是阴影部分面积的( )
A.2倍 B.3倍 C. D.
两位同学在解方程组时,甲同学由正确地解出,乙同学因把C写错了解得,那么a、b、c的正确的值应为( )
A.a=4,b=5,c=-1 B.a=4,b=5,c=-2
C.a=-4,b=-5,c=0 D.a=-4,b=-5,c=2
1 、多选题(本大题共2小题,共10分)
若多项式能用完全平方公式进行因式分解,则m的值为( )
A.2 B. C.6 D.
将一直角三角板与两边平行的纸条按如图所示放置,下列结论,正确的是( )
A.∠2=∠3
B.∠1+∠3=90°
C.∠2+∠4=180°
D.∠4+∠5=180°
1 、填空题(本大题共6小题,每小题4分,共24分)
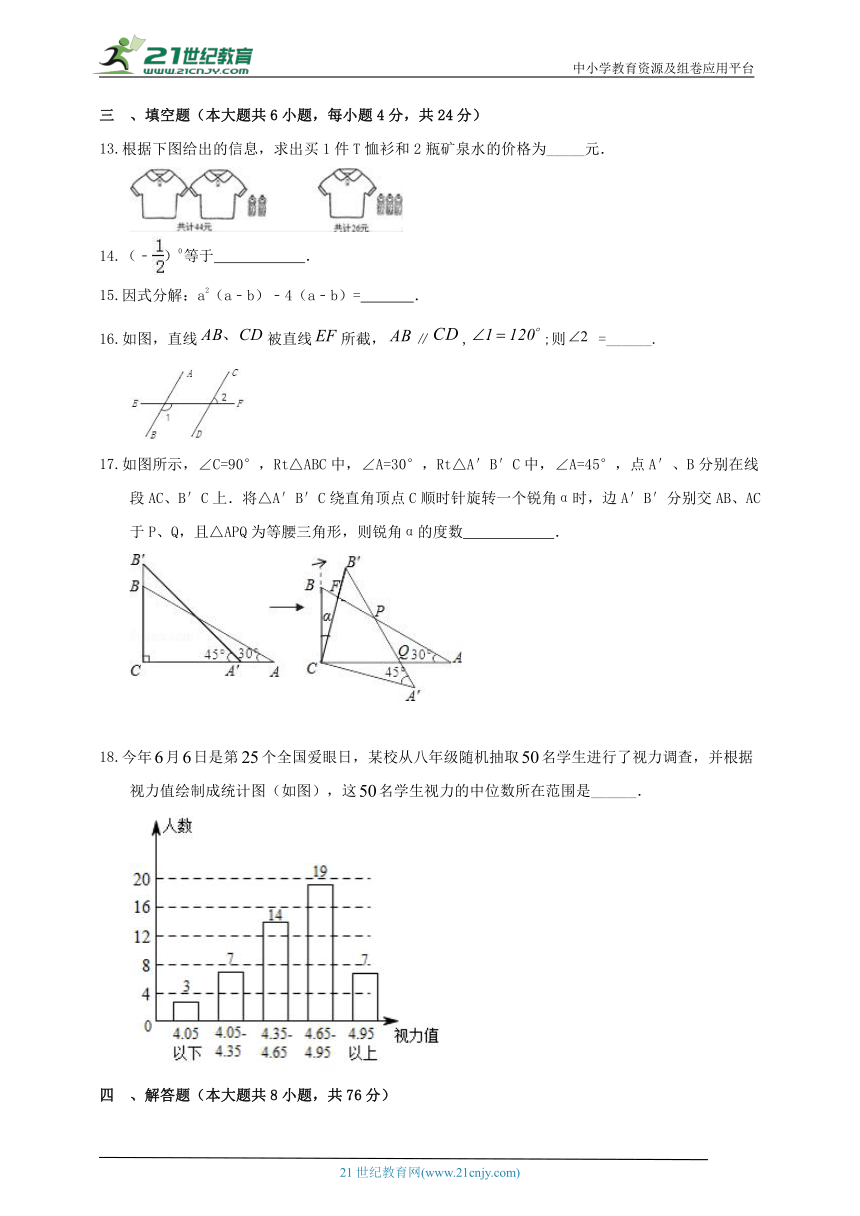
根据下图给出的信息,求出买1件T恤衫和2瓶矿泉水的价格为_____元.
(﹣)0等于 .
因式分解:a2(a﹣b)﹣4(a﹣b)= .
如图,直线被直线所截,∥,;则 =______.
如图所示,∠C=90°,Rt△ABC中,∠A=30°,Rt△A′B′C中,∠A=45°,点A′、B分别在线段AC、B′C上.将△A′B′C绕直角顶点C顺时针旋转一个锐角α时,边A′B′分别交AB、AC于P、Q,且△APQ为等腰三角形,则锐角α的度数 .
今年月日是第个全国爱眼日,某校从八年级随机抽取名学生进行了视力调查,并根据视力值绘制成统计图(如图),这名学生视力的中位数所在范围是______.
1 、解答题(本大题共8小题,共76分)
解方程组:.
先化简,再求值:[(2x+y)2﹣y(4x+y)]÷2x,其中x=﹣2.
如图,CD∥AB,∠DCB=75°,∠CBF=25°,∠EFB=130°,问直线EF与AB有怎样的位置关系?请说明理由.
某校为实现垃圾分类投放,准备在校园内摆放大、小两种垃圾桶购买2个大垃圾桶和4个小垃圾桶共需600元;购买6个大垃圾桶和8个小垃圾桶共需1560元.
(1)求大、小两种垃圾桶的单价;
(2)该校购买8个大垃圾桶和24个小垃圾桶共需多少元?
某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 面 试 体 能
甲 85 80 75
乙 80 90 73
丙 83 79 90
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
如图所示,已知三个村庄的位置如图3所示,经过商量,三个村庄决定联合打一眼机井向三个村庄供水,要想使机井到三个村庄的距离相等,机井应该设在何处?并说明你的理由。
阅读下列材料,并解决问题.
材料:两个正整数相除时,不一定都能整除,当不能整除时,就出现了余数.被除数、除数、商和余数之间有如下的关系:被除数=除数×商+余数(0≤余数<除数).类似的,关于x的多项式A(x)除以多项式B(x)时,一定存在一对多项式g(x)、r(x),使得A(x)=B(x) g(x)+r(x),其中余式r(x)的次数小于除式B(x)的次数.
例如:多项式x2+x+5除以多项式x+2,商为x﹣1,余式数为7,即有x2+x+5=(x+2)(x﹣1)+7.
又如:多项式x2+5x+6除以多项式x+2,商为x+3,余式数为0,即有x2+5x+6=(x+2)(x+3),此时,多项式x2+5x+6能被多项式x+2整除.
问题:
(1)多项式x2+2x﹣8除以多项式x﹣2,所得的商为 .
(2)多项式x2+7x+8除以多项式x+1,所得的余式数为2,则商为 .
(3)多项式2x3+ax2+bx﹣6分别能被x﹣1和x﹣2整除,则多项式2x3+ax2+bx﹣6除以(x﹣1)(x﹣2)的商为 .
在综合与实践课上,老师计同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.°
(1)如图(1),若三角尺的60°角的顶点G放在CD上,若∠2 = 2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明 ∠AEF与∠FGC间的数量关系;
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,∠CFG=β,则∠AEG与∠CFG的数量关系是什么?用含α,β的式子表示.
答案解析
1 、选择题
【考点】统计量的选择.
【分析】15人成绩的中位数是第8名的成绩.参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
解:由题意可得:
小明想要知道自己能否进入前8名,不仅要了解自己的成绩,还要了解这15名学生成绩的中位数,
故选D.
【点评】本题考查统计量的选择,解题的关键是明确题意,选取合适的统计量.
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【分析】根据合并同类项,可判断A,根据同底数幂的乘法,可判断B,根据同底数幂的除法,可判断C,根据幂的乘方,可判断D.
解:A.系数相加字母及指数不变,故A错误;
B、底数不变指数相加,故B错误;
C、底数不变指数相减,故C错误;
D、底数不变指数相乘,故D正确;
故选:D.
【点评】本题考查了同底数幂的除法,根据幂的运算法则计算是解题关键.
【考点】因式分解的意义
【分析】根据多项式x2+bx+c因式分解后的一个因式是(x+1),即可得到当x+1=0,即x= 1时,x2+bx+c=0,即1 b+c=0,即可得到b c的值.
解:为因式分解后的一个因式.
当,即时,,即,
,
.
故选:B.
【点评】本题主要考查了因式分解的意义,把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式.
【考点】补角的定义
【分析】在图中找出与∠AOD之和为180°的角即可.
解:两角之和为180°,则两角互补,
由图可知∠AOC、∠EOD、∠DOB与∠AOD互补.
故选:C.
【点评】考查了补角,解答本题的关键是熟记补角的定义.
【考点】轴对称的性质.
【分析】根据正方形的对称性解答.
解:正方形有4条对称轴.
故选:D.
【点评】本题考查了轴对称的性质,熟记正方形的对称性是解题的关键.
【考点】平均数,方差
【分析】根据平均数和方差的意义解答.
解:从平均数看,成绩好的同学有甲、乙,
从方差看甲、乙两人中,甲方差小,即甲发挥稳定,
故选:A.
【点评】本题考查了平均数和方差,熟悉它们的意义是解题的关键.
【考点】由实际问题抽象出二元一次方程组.
【分析】根据A.B两种商品共60件以及用1680元购进A.B两种商品分别得出等式组成方程组即可.
解:设购买A型商品x件、B型商品y件,依题意列方程组:
.
故选:B.
【点评】此题主要考查了由实际问题抽象出二元一次方程组,正确找出等量关系是解题关键.
【考点】平行线的性质
【分析】结合平行线的性质得出:∠1=∠3=∠4=40°,再利用翻折变换的性质得出答案.
解:由题意可得:∠1=∠3=∠4=40°,
则∠2=∠5==70°.
故选:D.
【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.
【考点】整式的混合运算
【分析】根据长方形的面积公式计算出阴影部分面积和空白部分的面积,即可得到结论.
解:空白部分的面积为:
阴影部分的面积为:
∴空白部分的面积是阴影部分面积的2倍.
故选:A
【点评】本题考查了整式的混合运算,正确识别图形搞清楚各部分的关系是解题的关键.
【考点】二元一次方程的解,解三元一次方程组
【分析】把代入得: ,把代入得:-2a+2b=2,组成方程组 解方程组即可.
解:把代入得: ,
把代入得:-2a+2b=2,
∴
解得:
故选:B.
【点评】本题考查二元一次方程组的解,解题关键是组成三元一次方程组.
1 、多选题
【考点】代数式求值,因式分解的应用
【分析】完全平方式:,根据完全平方式的特点建立方程即可得到答案.
解: 多项式能用完全平方公式进行因式分解,
或,
或
故选:BC.
【点评】本题考查的是利用完全平方公式分解因式,完全平方式的特点,掌握完全平方式的特点是解题的关键.
【考点】平行线的性质
【分析】根据两直线平行同位角相等,内错角相等,同旁内角互补,及直角三角板的特殊性解答.
解:纸条的两边平行,
∠4 +∠5 = 180°,∠3 =∠4,∠1 =∠2,
D选项正确;
又直角三角板在纸片上方,
∠2 +∠4 = 90°,
又∠3 =∠4,
∠2 +∠3 = 90°,
∠1 =∠2,
∠1+∠3 = 90°,
B选项正确.
故选:BD.
【点评】本题考查平行线的性质,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.
1 、填空题
【考点】二元一次方程组的应用
【分析】本题是一道图形结合题,要求买1件T恤衫和2瓶矿泉水的价格,就要先设出买1件T恤衫和1瓶矿泉水的价格,然后从图中找出等量关系,根据题意列方程组求解即可.
解:设买1件T恤衫和1瓶矿泉水的价格分别是x元,y元.
则,
解得.
所以买1件T恤衫和2瓶矿泉水的价格为24元.
故答案为:24.
【点评】本题考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.
【考点】零指数幂.
【分析】依据零指数幂的性质求解即可.
解:由零指数幂的性质可知:(﹣)0=1.
故答案为:1.
【点评】本题考查了零指数幂,要知道,任何非0数的0次幂为1.
【考点】因式分解﹣运用公式法
【分析】先提公因式,再利用平方差公式因式分解即可.
解:a2(a﹣b)﹣4(a﹣b)
=(a﹣b)(a2﹣4)
=(a﹣b)(a﹣2)(a+2),
故答案为:(a﹣b)(a﹣2)(a+2).
【点评】本题考查的是因式分解,掌握提公因式法、平方差公式进行因式分解是解题的关键.
【考点】平行线的性质
【分析】直接利用平角的定义结合平行线的性质得出答案.
解:如图,
∵∠1=120°,
∴∠3=180°-120°=60°,
∵AB∥CD,
∴∠2=∠3=60°.
故答案为:60°.
【点评】此题主要考查了平行线的性质,正确得出∠2=∠3是解题关键.
【考点】 旋转的性质;等腰三角形的性质.
【分析】 根据等腰三角形的性质得出∠QPA=∠A=30°,利用三角形外角性质得出∠PQC=60°=∠A'+∠QCA'=45°+α,解答即可.
解:∵△APQ为等腰三角形,∠A=30°,
∴∠QPA=∠A=30°,
∴∠PQC=60°=∠A'+∠QCA'=45°+α,
∴α=15°.
故答案为:15°.
【点评】 此题考查旋转的性质,关键是根据等腰三角形的性质得出∠QPA=∠A=30°,利用三角形外角性质得出∠PQC=60°=∠A'+∠QCA'=45°+α.
【考点】频数(率)分布直方图,中位数
【分析】根据频率直方图的数据和中位数概念可知,在这50个数据的中位数位于第四组,据此求解即可.
解:由中位数概念知道这个数据位于中间位置,共50个数据,根据频率直方图的数据可知,中位数位于第四组,即这名学生视力的中位数所在范围是4.65-4.95.
故答案为:4.65-4.95.
【点评】本题考查学生对频率直方图的认识和应用,以及对中位数的理解,熟悉相关性质是解题的关键.
1 、解答题
【考点】解二元一次方程组.
【分析】方程组利用加减消元法求出解即可.
解:,
①×3+②得:5x=10,即x=2,
把x=2代入①得:y=1,
则方程组的解为.
【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
【考点】整式的混合运算—化简求值.
【分析】先算乘法,再合并同类项,算除法,最后代入求出即可.
解:[(2x+y)2﹣y(4x+y)]÷2x
=[4x2+4xy+y2﹣4xy﹣y2]÷2x
=4x2÷2x
=2x,
当x=﹣2时,原式=2×(﹣2)=﹣4.
【点评】本题考查了整式的混合运算和求值的应用,主要考查学生的计算和化简能力,难度适中.
【考点】平行线的判定与性质
【分析】两直线的位置关系有两种:平行和相交,根据图形可以可以猜想两直线平行,然后根据已知探求平行的判定条件.
解:EF∥AB,
理由如下:∵CD∥AB,∠DCB=75°
∴∠CBA=∠DCB=75°(两直线平行,内错角相等)
∵∠FBA=∠CBA-∠CBF, ∠CBF=25°
∴∠FBA=75°-25°=50°
∵∠EFB=130°
∴∠FBA+∠EFB=180°
∴EF∥AB(同旁内角互补,两直线平行)
【点评】本题主要考查平行线的判定与性质定理,掌握平行线的判定与性质是解答本题的关键,即①同位角相等两直线平行,②内错角相等两直线平行,③同旁内角互补两直线平行,④a∥b,b∥ca∥c.
【考点】二元一次方程组的应用
【分析】(1)根据题意列出二元一次方程组求解即可.
(2)根据第(1)问求得的大小垃圾桶的单价计算即可.
解:(1)设大垃圾桶的单价为x元,小垃圾桶的单价为y元,
由题意列方程得,
解得,
答:大垃圾桶的单价为180元,小垃圾桶的单价为60元.
(2).
答:该校购买8个大垃圾桶和24个小垃圾桶共需2880元.
【点评】此题考查了二元一次方程组应用题,解题的关键是分析出题目中的等量关系.
【考点】算术平均数,加权平均数
【分析】(1)代入求平均数公式即可求出三人的平均成绩,比较得出结果;
(2)先算出甲、乙、丙的总分,根据公司的规定先排除丙,再根据甲的总分最高,即可得出甲被录用.
解:(1)甲=(85+80+75)÷3=80(分),乙=(80+90+73)÷3=81(分),丙=(83+79+90)÷3=84(分),则从高到低确定三名应聘者的排名顺序为:丙,乙,甲;
(2)甲的总分是:85×60%+80×30%+75×10%=82.5(分),乙的总分是:80×60%+90×30%+73×10%=82.3(分),丙的总分是:83×60%+79×30%+90×10%=82.5(分).
∵公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,
∴丙排除,
∴甲的总分最高,甲被录用.
【点评】本题考查了算术平均数和加权平均数的计算.平均数等于所有数据的和除以数据的个数.
【考点】利用轴对称设计图案
【分析】可以分开考虑,与A.B距离相等的点在线段AB的垂直平分线上,与A.C距离相等的点在线段AC的垂直平分线上。因为同时需要满足到A.B、C三点的距离相等,所以机井应该设在这两条垂直平分线的交点处。
解:如图所示,
(1)连结AC、AB;
(2)作AC的垂直平分线交AC于点F,作AB的垂直平分线交AB于点E,两条垂直平分线相交于点M,点M就是机井的位置。
理由:因为ME垂直平分AB,所以MA=MB;
因为MF垂直平分AC,所以MA=MC;
所以MA=MB= MC,
所以点M到三个村庄的距离相等
【点评】本题考查了线段垂直平分线的性质及作法,熟练掌握线段垂直平分线的性质是解题的关键。
【考点】因式分解的应用,多项式乘多项式,整式的除法
【分析】(1)把已知多项式分解因式即可求解,
(2)首先把已知多项式减去余式再分解因式即可求解,
(3)设2x3+ax2+bx﹣6=(x﹣1)(x﹣2) A,其中A为一次多项式,然后把x=1和x=2时,代入等式可以得到关于a、b的方程组,解方程组求出a,b,最后分解因式即可求解.
解:(1)∵x2+2x﹣8=(x+4)(x﹣2),
∴多项式x2+2x﹣8除以多项式x﹣2,所得的商为x+4,
(2)∵x2+7x+8﹣2=x2+7x+6=(x+1)(x+6),
∴x2+7x+8=(x+1)(x+6)+2,
∴多项式x2+7x+8除以多项式x+1,所得的余式数为2,则商为x+6,
(3)∵多项式2x3+ax2+bx﹣6分别能被x﹣1和x﹣2整除,
∴设2x3+ax2+bx﹣6=(x﹣1)(x﹣2) A,其中A为一次多项式,
当x=1时,2+a+b﹣6=0,
当x=2时,16+4a+2b﹣6=0,
联立解得:,
∴2x3+ax2+bx﹣6
=2x3﹣9x2+13x﹣6,
=2x3﹣5x2+3x﹣4x2+10x﹣6,
=x(2x﹣3)(x﹣1)﹣2(2x﹣3)(x﹣1)
=(2x﹣3)(x﹣1)(x﹣2),
∴多项式2x3+ax2+bx﹣6除以(x﹣1)(x﹣2)的商为2x﹣3.
故答案为:(1)x+4,(2)x+6,(3)2x﹣3.
【点评】此题主要考查了因式分解的应用,正确读懂题意是解题的关键.
【考点】平行线的判定与性质
【分析】(1)根据平行线的性质可知∠1=∠EGD,依据∠2+∠FGE+∠EGD=180°,可求出∠1的度数;
(2)过点F作FP∥AB,得到FP∥AB∥CD,通过平行线的性质把∠AEF和∠FGC转化到∠EFG上即可;
(3)依据AB∥CD,可知∠AEF+∠CFE=180°,再代入∠AEF=∠AEG 30°,∠CFE=∠CFG 90°,即可求出∠AEG+∠CFG=300°,进而即可得到结论.
解:(1)∵AB∥CD,
∴∠1=∠EGD,
∵∠2+∠FGE+∠EGD=180°,∠2=2∠1,
∴2∠1+60°+∠1=180°,解得∠1=40°;
(2)∠AEF+∠FGC=90°,理由如下:
如图,过点F作FP∥AB,
∵CD∥AB,
∴FP∥AB∥CD,
∴∠AEF=∠EFP,∠FGC=∠GFP,
∴∠AEF+∠FGC=∠EFP+∠GFP=∠EFG,
∵∠EFG=90°,
∴∠AEF+∠FGC=90°;
(3)α+β=300°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴∠AEG ∠FEG+∠CFG ∠EFG=180°,
∵∠FEG=30°,∠EFG=90°,
∴∠AEG 30°+∠CFG 90°=180°,
∴∠AEG+∠CFG=300°,即:α+β=300°.
【点评】本题主要考查了平行线的性质,熟练掌握平行线的性质定理,正确作出辅助线是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版2022-2023学年度下学期七年级期末练习数学试5
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
在我市举办的中学生“争做文明盘锦人”演讲比赛中,有15名学生进入决赛,他们决赛的成绩各不相同,小明想知道自己能否进入前8名,不仅要了解自己的成绩,还要了解这15名学生成绩的( )
A.众数 B.方差 C.平均数 D.中位数
下列计算正确的是( )
A. a2+a2=a4 B. a2 a3=a6 C. a3÷a=a3 D. (a3)3=a9
若多项式因式分解后的一个因式是,则的值是( )
A. B. C. D.
如图,直线AB、CD相交于点O,OD平分∠BOE,则∠AOD的补角的个数为( )
A.1 个 B.2 个 C.3 个 D.4 个
正方形的对称轴的条数为( )
A.1 B.2 C.3 D.4
甲、乙、丙、丁四名同学在一次投掷实心球训练中,在相同条件下各投掷10次,他们成绩的平均数与方差s2如下表:
甲 乙 丙 丁
平均数(环) 11.1 11.1 10.9 10.9
方差s2 1.1 1.2 1.3 1.4
若要选一名成绩好且发挥稳定的同学参加比赛,则应该选择( )
A.甲 B.乙 C.丙 D.丁
端午节前夕,某超市用1680元购进A.B两种商品共60件,其中A型商品每件24元,B型商品每件36元.设购买A型商品x件、B型商品y件,依题意列方程组正确的是( )
A. B.C. D.
将一个矩形纸片按如图所示折叠,若∠1=40°,则∠2的度数是( )
A.40° B.50° C.60° D.70°
一张长方形餐桌的表面如图所示,图中空白部分的面积是阴影部分面积的( )
A.2倍 B.3倍 C. D.
两位同学在解方程组时,甲同学由正确地解出,乙同学因把C写错了解得,那么a、b、c的正确的值应为( )
A.a=4,b=5,c=-1 B.a=4,b=5,c=-2
C.a=-4,b=-5,c=0 D.a=-4,b=-5,c=2
1 、多选题(本大题共2小题,共10分)
若多项式能用完全平方公式进行因式分解,则m的值为( )
A.2 B. C.6 D.
将一直角三角板与两边平行的纸条按如图所示放置,下列结论,正确的是( )
A.∠2=∠3
B.∠1+∠3=90°
C.∠2+∠4=180°
D.∠4+∠5=180°
1 、填空题(本大题共6小题,每小题4分,共24分)
根据下图给出的信息,求出买1件T恤衫和2瓶矿泉水的价格为_____元.
(﹣)0等于 .
因式分解:a2(a﹣b)﹣4(a﹣b)= .
如图,直线被直线所截,∥,;则 =______.
如图所示,∠C=90°,Rt△ABC中,∠A=30°,Rt△A′B′C中,∠A=45°,点A′、B分别在线段AC、B′C上.将△A′B′C绕直角顶点C顺时针旋转一个锐角α时,边A′B′分别交AB、AC于P、Q,且△APQ为等腰三角形,则锐角α的度数 .
今年月日是第个全国爱眼日,某校从八年级随机抽取名学生进行了视力调查,并根据视力值绘制成统计图(如图),这名学生视力的中位数所在范围是______.
1 、解答题(本大题共8小题,共76分)
解方程组:.
先化简,再求值:[(2x+y)2﹣y(4x+y)]÷2x,其中x=﹣2.
如图,CD∥AB,∠DCB=75°,∠CBF=25°,∠EFB=130°,问直线EF与AB有怎样的位置关系?请说明理由.
某校为实现垃圾分类投放,准备在校园内摆放大、小两种垃圾桶购买2个大垃圾桶和4个小垃圾桶共需600元;购买6个大垃圾桶和8个小垃圾桶共需1560元.
(1)求大、小两种垃圾桶的单价;
(2)该校购买8个大垃圾桶和24个小垃圾桶共需多少元?
某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 面 试 体 能
甲 85 80 75
乙 80 90 73
丙 83 79 90
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
如图所示,已知三个村庄的位置如图3所示,经过商量,三个村庄决定联合打一眼机井向三个村庄供水,要想使机井到三个村庄的距离相等,机井应该设在何处?并说明你的理由。
阅读下列材料,并解决问题.
材料:两个正整数相除时,不一定都能整除,当不能整除时,就出现了余数.被除数、除数、商和余数之间有如下的关系:被除数=除数×商+余数(0≤余数<除数).类似的,关于x的多项式A(x)除以多项式B(x)时,一定存在一对多项式g(x)、r(x),使得A(x)=B(x) g(x)+r(x),其中余式r(x)的次数小于除式B(x)的次数.
例如:多项式x2+x+5除以多项式x+2,商为x﹣1,余式数为7,即有x2+x+5=(x+2)(x﹣1)+7.
又如:多项式x2+5x+6除以多项式x+2,商为x+3,余式数为0,即有x2+5x+6=(x+2)(x+3),此时,多项式x2+5x+6能被多项式x+2整除.
问题:
(1)多项式x2+2x﹣8除以多项式x﹣2,所得的商为 .
(2)多项式x2+7x+8除以多项式x+1,所得的余式数为2,则商为 .
(3)多项式2x3+ax2+bx﹣6分别能被x﹣1和x﹣2整除,则多项式2x3+ax2+bx﹣6除以(x﹣1)(x﹣2)的商为 .
在综合与实践课上,老师计同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.°
(1)如图(1),若三角尺的60°角的顶点G放在CD上,若∠2 = 2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明 ∠AEF与∠FGC间的数量关系;
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,∠CFG=β,则∠AEG与∠CFG的数量关系是什么?用含α,β的式子表示.
答案解析
1 、选择题
【考点】统计量的选择.
【分析】15人成绩的中位数是第8名的成绩.参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
解:由题意可得:
小明想要知道自己能否进入前8名,不仅要了解自己的成绩,还要了解这15名学生成绩的中位数,
故选D.
【点评】本题考查统计量的选择,解题的关键是明确题意,选取合适的统计量.
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【分析】根据合并同类项,可判断A,根据同底数幂的乘法,可判断B,根据同底数幂的除法,可判断C,根据幂的乘方,可判断D.
解:A.系数相加字母及指数不变,故A错误;
B、底数不变指数相加,故B错误;
C、底数不变指数相减,故C错误;
D、底数不变指数相乘,故D正确;
故选:D.
【点评】本题考查了同底数幂的除法,根据幂的运算法则计算是解题关键.
【考点】因式分解的意义
【分析】根据多项式x2+bx+c因式分解后的一个因式是(x+1),即可得到当x+1=0,即x= 1时,x2+bx+c=0,即1 b+c=0,即可得到b c的值.
解:为因式分解后的一个因式.
当,即时,,即,
,
.
故选:B.
【点评】本题主要考查了因式分解的意义,把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式.
【考点】补角的定义
【分析】在图中找出与∠AOD之和为180°的角即可.
解:两角之和为180°,则两角互补,
由图可知∠AOC、∠EOD、∠DOB与∠AOD互补.
故选:C.
【点评】考查了补角,解答本题的关键是熟记补角的定义.
【考点】轴对称的性质.
【分析】根据正方形的对称性解答.
解:正方形有4条对称轴.
故选:D.
【点评】本题考查了轴对称的性质,熟记正方形的对称性是解题的关键.
【考点】平均数,方差
【分析】根据平均数和方差的意义解答.
解:从平均数看,成绩好的同学有甲、乙,
从方差看甲、乙两人中,甲方差小,即甲发挥稳定,
故选:A.
【点评】本题考查了平均数和方差,熟悉它们的意义是解题的关键.
【考点】由实际问题抽象出二元一次方程组.
【分析】根据A.B两种商品共60件以及用1680元购进A.B两种商品分别得出等式组成方程组即可.
解:设购买A型商品x件、B型商品y件,依题意列方程组:
.
故选:B.
【点评】此题主要考查了由实际问题抽象出二元一次方程组,正确找出等量关系是解题关键.
【考点】平行线的性质
【分析】结合平行线的性质得出:∠1=∠3=∠4=40°,再利用翻折变换的性质得出答案.
解:由题意可得:∠1=∠3=∠4=40°,
则∠2=∠5==70°.
故选:D.
【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.
【考点】整式的混合运算
【分析】根据长方形的面积公式计算出阴影部分面积和空白部分的面积,即可得到结论.
解:空白部分的面积为:
阴影部分的面积为:
∴空白部分的面积是阴影部分面积的2倍.
故选:A
【点评】本题考查了整式的混合运算,正确识别图形搞清楚各部分的关系是解题的关键.
【考点】二元一次方程的解,解三元一次方程组
【分析】把代入得: ,把代入得:-2a+2b=2,组成方程组 解方程组即可.
解:把代入得: ,
把代入得:-2a+2b=2,
∴
解得:
故选:B.
【点评】本题考查二元一次方程组的解,解题关键是组成三元一次方程组.
1 、多选题
【考点】代数式求值,因式分解的应用
【分析】完全平方式:,根据完全平方式的特点建立方程即可得到答案.
解: 多项式能用完全平方公式进行因式分解,
或,
或
故选:BC.
【点评】本题考查的是利用完全平方公式分解因式,完全平方式的特点,掌握完全平方式的特点是解题的关键.
【考点】平行线的性质
【分析】根据两直线平行同位角相等,内错角相等,同旁内角互补,及直角三角板的特殊性解答.
解:纸条的两边平行,
∠4 +∠5 = 180°,∠3 =∠4,∠1 =∠2,
D选项正确;
又直角三角板在纸片上方,
∠2 +∠4 = 90°,
又∠3 =∠4,
∠2 +∠3 = 90°,
∠1 =∠2,
∠1+∠3 = 90°,
B选项正确.
故选:BD.
【点评】本题考查平行线的性质,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.
1 、填空题
【考点】二元一次方程组的应用
【分析】本题是一道图形结合题,要求买1件T恤衫和2瓶矿泉水的价格,就要先设出买1件T恤衫和1瓶矿泉水的价格,然后从图中找出等量关系,根据题意列方程组求解即可.
解:设买1件T恤衫和1瓶矿泉水的价格分别是x元,y元.
则,
解得.
所以买1件T恤衫和2瓶矿泉水的价格为24元.
故答案为:24.
【点评】本题考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.
【考点】零指数幂.
【分析】依据零指数幂的性质求解即可.
解:由零指数幂的性质可知:(﹣)0=1.
故答案为:1.
【点评】本题考查了零指数幂,要知道,任何非0数的0次幂为1.
【考点】因式分解﹣运用公式法
【分析】先提公因式,再利用平方差公式因式分解即可.
解:a2(a﹣b)﹣4(a﹣b)
=(a﹣b)(a2﹣4)
=(a﹣b)(a﹣2)(a+2),
故答案为:(a﹣b)(a﹣2)(a+2).
【点评】本题考查的是因式分解,掌握提公因式法、平方差公式进行因式分解是解题的关键.
【考点】平行线的性质
【分析】直接利用平角的定义结合平行线的性质得出答案.
解:如图,
∵∠1=120°,
∴∠3=180°-120°=60°,
∵AB∥CD,
∴∠2=∠3=60°.
故答案为:60°.
【点评】此题主要考查了平行线的性质,正确得出∠2=∠3是解题关键.
【考点】 旋转的性质;等腰三角形的性质.
【分析】 根据等腰三角形的性质得出∠QPA=∠A=30°,利用三角形外角性质得出∠PQC=60°=∠A'+∠QCA'=45°+α,解答即可.
解:∵△APQ为等腰三角形,∠A=30°,
∴∠QPA=∠A=30°,
∴∠PQC=60°=∠A'+∠QCA'=45°+α,
∴α=15°.
故答案为:15°.
【点评】 此题考查旋转的性质,关键是根据等腰三角形的性质得出∠QPA=∠A=30°,利用三角形外角性质得出∠PQC=60°=∠A'+∠QCA'=45°+α.
【考点】频数(率)分布直方图,中位数
【分析】根据频率直方图的数据和中位数概念可知,在这50个数据的中位数位于第四组,据此求解即可.
解:由中位数概念知道这个数据位于中间位置,共50个数据,根据频率直方图的数据可知,中位数位于第四组,即这名学生视力的中位数所在范围是4.65-4.95.
故答案为:4.65-4.95.
【点评】本题考查学生对频率直方图的认识和应用,以及对中位数的理解,熟悉相关性质是解题的关键.
1 、解答题
【考点】解二元一次方程组.
【分析】方程组利用加减消元法求出解即可.
解:,
①×3+②得:5x=10,即x=2,
把x=2代入①得:y=1,
则方程组的解为.
【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
【考点】整式的混合运算—化简求值.
【分析】先算乘法,再合并同类项,算除法,最后代入求出即可.
解:[(2x+y)2﹣y(4x+y)]÷2x
=[4x2+4xy+y2﹣4xy﹣y2]÷2x
=4x2÷2x
=2x,
当x=﹣2时,原式=2×(﹣2)=﹣4.
【点评】本题考查了整式的混合运算和求值的应用,主要考查学生的计算和化简能力,难度适中.
【考点】平行线的判定与性质
【分析】两直线的位置关系有两种:平行和相交,根据图形可以可以猜想两直线平行,然后根据已知探求平行的判定条件.
解:EF∥AB,
理由如下:∵CD∥AB,∠DCB=75°
∴∠CBA=∠DCB=75°(两直线平行,内错角相等)
∵∠FBA=∠CBA-∠CBF, ∠CBF=25°
∴∠FBA=75°-25°=50°
∵∠EFB=130°
∴∠FBA+∠EFB=180°
∴EF∥AB(同旁内角互补,两直线平行)
【点评】本题主要考查平行线的判定与性质定理,掌握平行线的判定与性质是解答本题的关键,即①同位角相等两直线平行,②内错角相等两直线平行,③同旁内角互补两直线平行,④a∥b,b∥ca∥c.
【考点】二元一次方程组的应用
【分析】(1)根据题意列出二元一次方程组求解即可.
(2)根据第(1)问求得的大小垃圾桶的单价计算即可.
解:(1)设大垃圾桶的单价为x元,小垃圾桶的单价为y元,
由题意列方程得,
解得,
答:大垃圾桶的单价为180元,小垃圾桶的单价为60元.
(2).
答:该校购买8个大垃圾桶和24个小垃圾桶共需2880元.
【点评】此题考查了二元一次方程组应用题,解题的关键是分析出题目中的等量关系.
【考点】算术平均数,加权平均数
【分析】(1)代入求平均数公式即可求出三人的平均成绩,比较得出结果;
(2)先算出甲、乙、丙的总分,根据公司的规定先排除丙,再根据甲的总分最高,即可得出甲被录用.
解:(1)甲=(85+80+75)÷3=80(分),乙=(80+90+73)÷3=81(分),丙=(83+79+90)÷3=84(分),则从高到低确定三名应聘者的排名顺序为:丙,乙,甲;
(2)甲的总分是:85×60%+80×30%+75×10%=82.5(分),乙的总分是:80×60%+90×30%+73×10%=82.3(分),丙的总分是:83×60%+79×30%+90×10%=82.5(分).
∵公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,
∴丙排除,
∴甲的总分最高,甲被录用.
【点评】本题考查了算术平均数和加权平均数的计算.平均数等于所有数据的和除以数据的个数.
【考点】利用轴对称设计图案
【分析】可以分开考虑,与A.B距离相等的点在线段AB的垂直平分线上,与A.C距离相等的点在线段AC的垂直平分线上。因为同时需要满足到A.B、C三点的距离相等,所以机井应该设在这两条垂直平分线的交点处。
解:如图所示,
(1)连结AC、AB;
(2)作AC的垂直平分线交AC于点F,作AB的垂直平分线交AB于点E,两条垂直平分线相交于点M,点M就是机井的位置。
理由:因为ME垂直平分AB,所以MA=MB;
因为MF垂直平分AC,所以MA=MC;
所以MA=MB= MC,
所以点M到三个村庄的距离相等
【点评】本题考查了线段垂直平分线的性质及作法,熟练掌握线段垂直平分线的性质是解题的关键。
【考点】因式分解的应用,多项式乘多项式,整式的除法
【分析】(1)把已知多项式分解因式即可求解,
(2)首先把已知多项式减去余式再分解因式即可求解,
(3)设2x3+ax2+bx﹣6=(x﹣1)(x﹣2) A,其中A为一次多项式,然后把x=1和x=2时,代入等式可以得到关于a、b的方程组,解方程组求出a,b,最后分解因式即可求解.
解:(1)∵x2+2x﹣8=(x+4)(x﹣2),
∴多项式x2+2x﹣8除以多项式x﹣2,所得的商为x+4,
(2)∵x2+7x+8﹣2=x2+7x+6=(x+1)(x+6),
∴x2+7x+8=(x+1)(x+6)+2,
∴多项式x2+7x+8除以多项式x+1,所得的余式数为2,则商为x+6,
(3)∵多项式2x3+ax2+bx﹣6分别能被x﹣1和x﹣2整除,
∴设2x3+ax2+bx﹣6=(x﹣1)(x﹣2) A,其中A为一次多项式,
当x=1时,2+a+b﹣6=0,
当x=2时,16+4a+2b﹣6=0,
联立解得:,
∴2x3+ax2+bx﹣6
=2x3﹣9x2+13x﹣6,
=2x3﹣5x2+3x﹣4x2+10x﹣6,
=x(2x﹣3)(x﹣1)﹣2(2x﹣3)(x﹣1)
=(2x﹣3)(x﹣1)(x﹣2),
∴多项式2x3+ax2+bx﹣6除以(x﹣1)(x﹣2)的商为2x﹣3.
故答案为:(1)x+4,(2)x+6,(3)2x﹣3.
【点评】此题主要考查了因式分解的应用,正确读懂题意是解题的关键.
【考点】平行线的判定与性质
【分析】(1)根据平行线的性质可知∠1=∠EGD,依据∠2+∠FGE+∠EGD=180°,可求出∠1的度数;
(2)过点F作FP∥AB,得到FP∥AB∥CD,通过平行线的性质把∠AEF和∠FGC转化到∠EFG上即可;
(3)依据AB∥CD,可知∠AEF+∠CFE=180°,再代入∠AEF=∠AEG 30°,∠CFE=∠CFG 90°,即可求出∠AEG+∠CFG=300°,进而即可得到结论.
解:(1)∵AB∥CD,
∴∠1=∠EGD,
∵∠2+∠FGE+∠EGD=180°,∠2=2∠1,
∴2∠1+60°+∠1=180°,解得∠1=40°;
(2)∠AEF+∠FGC=90°,理由如下:
如图,过点F作FP∥AB,
∵CD∥AB,
∴FP∥AB∥CD,
∴∠AEF=∠EFP,∠FGC=∠GFP,
∴∠AEF+∠FGC=∠EFP+∠GFP=∠EFG,
∵∠EFG=90°,
∴∠AEF+∠FGC=90°;
(3)α+β=300°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴∠AEG ∠FEG+∠CFG ∠EFG=180°,
∵∠FEG=30°,∠EFG=90°,
∴∠AEG 30°+∠CFG 90°=180°,
∴∠AEG+∠CFG=300°,即:α+β=300°.
【点评】本题主要考查了平行线的性质,熟练掌握平行线的性质定理,正确作出辅助线是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
