湘教版2022-2023学年度下学期八年级期末练习数学试1(含解析)
文档属性
| 名称 | 湘教版2022-2023学年度下学期八年级期末练习数学试1(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-08 18:10:53 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
湘教版2022-2023学年度下学期八年级期末练习数学试1
姓名:__________班级:__________考号:__________总分__________
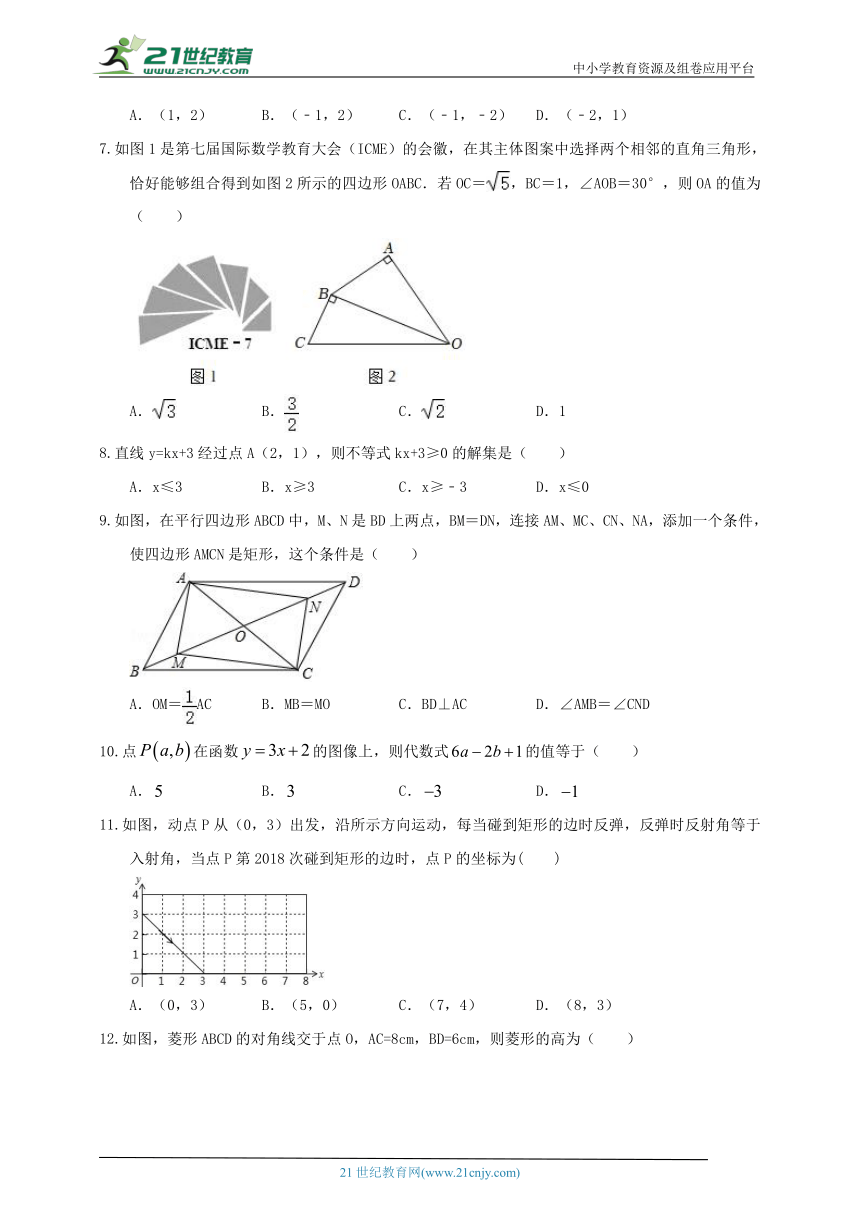
1 、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
下列给出的式子中,x是自变量的是( )
A.x=5 B.2x+y=0 C.2y2=4x+3 D.y=3x﹣1
下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
A. B. C. D.
如果一个正多边形的内角和等于外角和2倍,则这个正多边形是( )
A.正方形 B.正五边形 C.正六边形 D.正八边形
为庆祝建党99周年,某校八年级(3)班团支部为了让同学们进一步了解中国科技的发展,给班上同学布置了一项课外作业,从选出的以下五个内容中任选部分内容进行手抄报的制作:、“北斗卫星”:、“时代”;、“智轨快运系统”;、“东风快递”;、“高铁”.统计同学们所选内容的频数,绘制如图所示的折线统计图,则选择“时代”的频率是( )
A.0.25 B.0.3 C.25 D.30
如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∠ACD=30°,那么下列结论正确的是( )
A.AD=CD B.AC=AB C.BD=BC D.CD=AB
点P(1,﹣2)关于y轴对称的点的坐标是( )
A.(1,2) B.(﹣1,2) C.(﹣1,﹣2) D.(﹣2,1)
如图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形OABC.若OC=,BC=1,∠AOB=30°,则OA的值为( )
A. B. C. D.1
直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )
A.x≤3 B.x≥3 C.x≥﹣3 D.x≤0
如图,在平行四边形ABCD中,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )
A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND
点在函数的图像上,则代数式的值等于( )
A. B. C. D.
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2018次碰到矩形的边时,点P的坐标为( )
A.(0,3) B.(5,0) C.(7,4) D.(8,3)
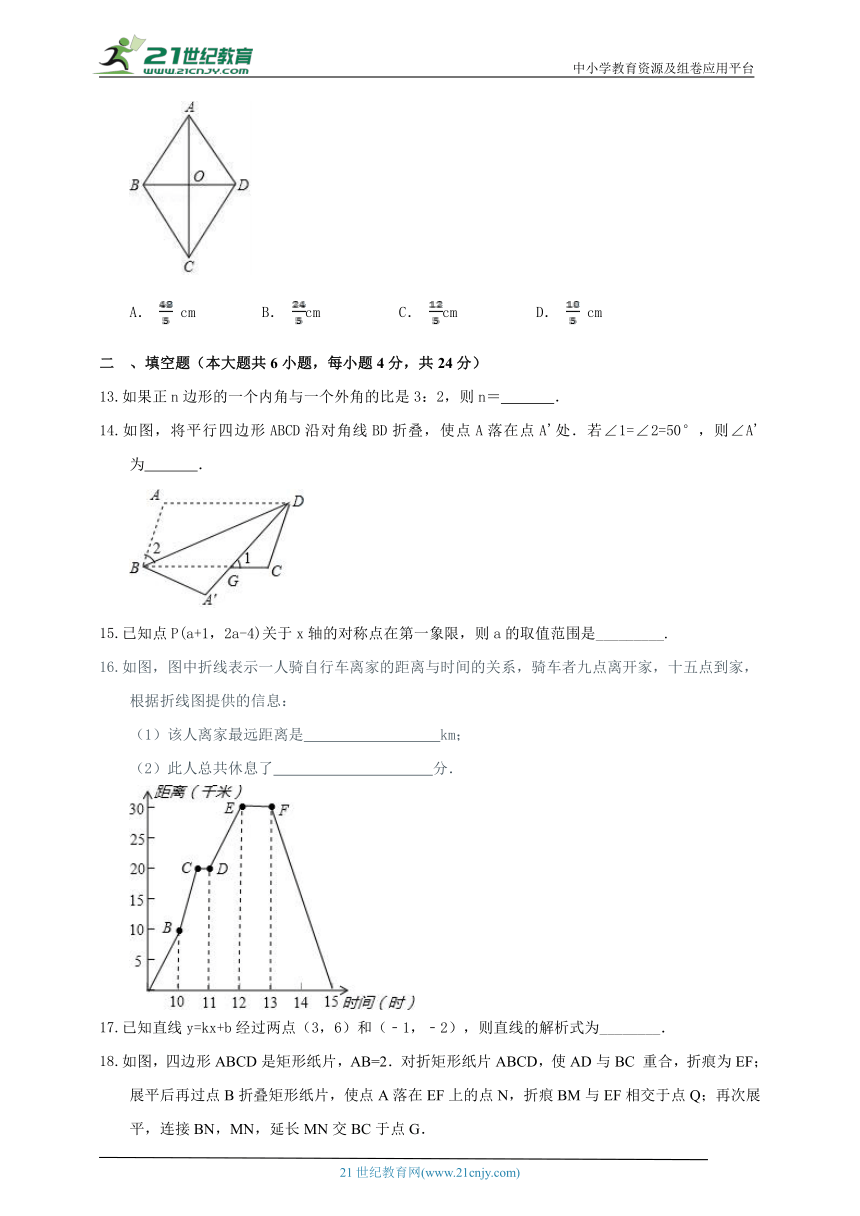
如图,菱形ABCD的对角线交于点O,AC=8cm,BD=6cm,则菱形的高为( )
A. cm B. cm C. cm D. cm
1 、填空题(本大题共6小题,每小题4分,共24分)
如果正n边形的一个内角与一个外角的比是3:2,则n= .
如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点A'处.若∠1=∠2=50°,则∠A'为 .
已知点P(a+1,2a-4)关于x轴的对称点在第一象限,则a的取值范围是_________.
如图,图中折线表示一人骑自行车离家的距离与时间的关系,骑车者九点离开家,十五点到家,根据折线图提供的信息:
(1)该人离家最远距离是 km;
(2)此人总共休息了 分.
已知直线y=kx+b经过两点(3,6)和(﹣1,﹣2),则直线的解析式为________.
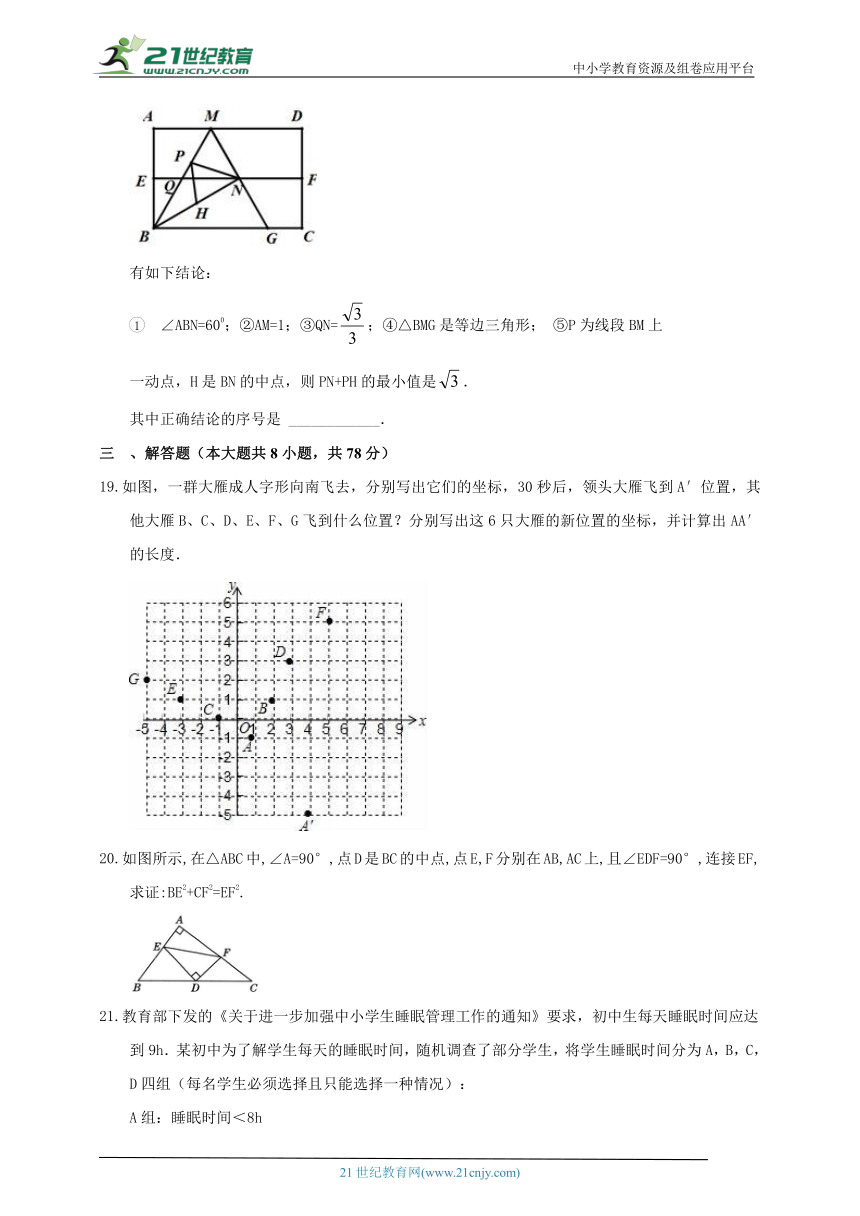
如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC 重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.
有如下结论:
1 ∠ABN=600;②AM=1;③QN=;④△BMG是等边三角形; ⑤P为线段BM上
一动点,H是BN的中点,则PN+PH的最小值是.
其中正确结论的序号是 ____________.
1 、解答题(本大题共8小题,共78分)
如图,一群大雁成人字形向南飞去,分别写出它们的坐标,30秒后,领头大雁飞到A′位置,其他大雁B、C、D、E、F、G飞到什么位置?分别写出这6只大雁的新位置的坐标,并计算出AA′的长度.
如图所示,在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,求证:BE2+CF2=EF2.
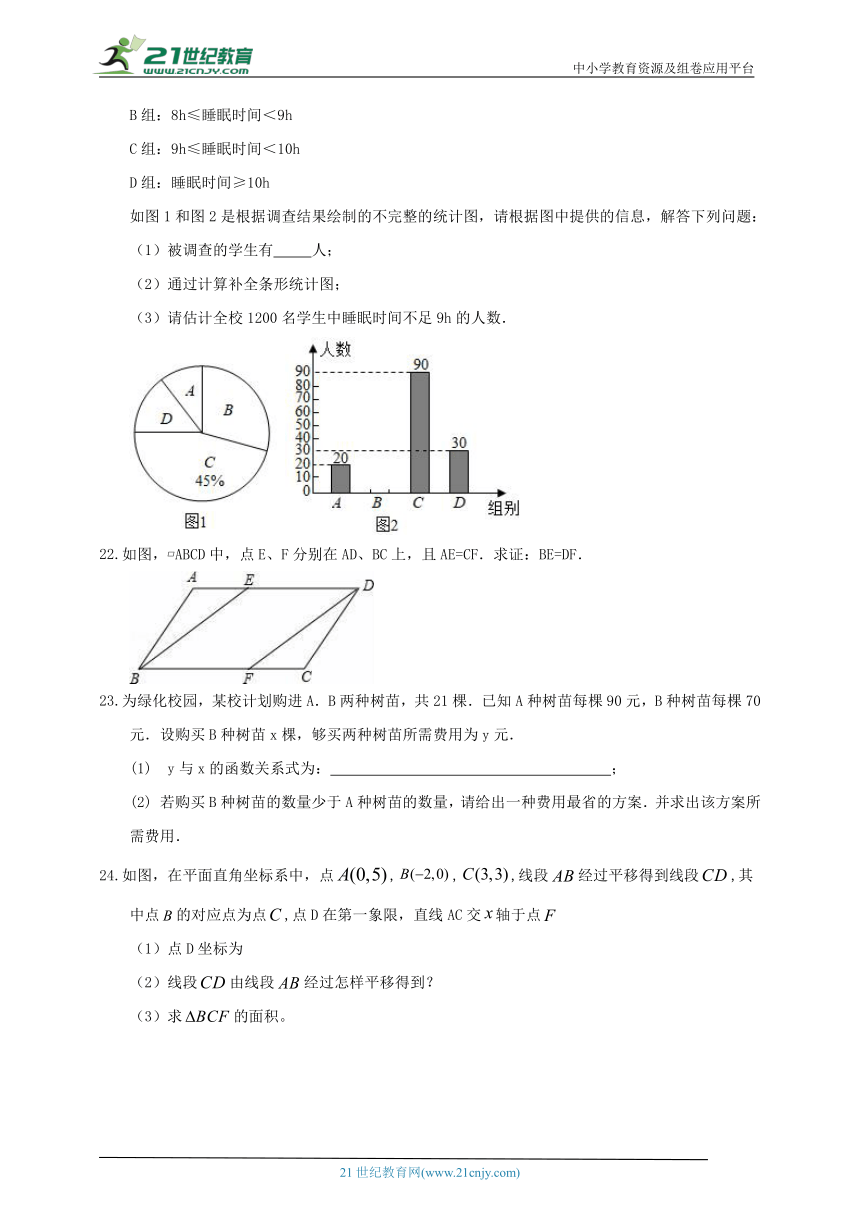
教育部下发的《关于进一步加强中小学生睡眠管理工作的通知》要求,初中生每天睡眠时间应达到9h.某初中为了解学生每天的睡眠时间,随机调查了部分学生,将学生睡眠时间分为A,B,C,D四组(每名学生必须选择且只能选择一种情况):
A组:睡眠时间<8h
B组:8h≤睡眠时间<9h
C组:9h≤睡眠时间<10h
D组:睡眠时间≥10h
如图1和图2是根据调查结果绘制的不完整的统计图,请根据图中提供的信息,解答下列问题:
(1)被调查的学生有 人;
(2)通过计算补全条形统计图;
(3)请估计全校1200名学生中睡眠时间不足9h的人数.
如图, ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:BE=DF.
为绿化校园,某校计划购进A.B两种树苗,共21棵.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,够买两种树苗所需费用为y元.
(1) y与x的函数关系式为: ;
(2) 若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案.并求出该方案所需费用.
如图,在平面直角坐标系中,点,,,线段经过平移得到线段,其中点的对应点为点,点D在第一象限,直线AC交轴于点
(1)点D坐标为
(2)线段由线段经过怎样平移得到?
(3)求的面积。
如图,在四边形ABCD中,AD∥BC,∠A=∠C,点P在边AB上.
(1)判断四边形ABCD的形状并加以证明;
(2)若AB=AD,以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B′、C′上,且B′C′经过点D,折痕与四边形的另一交点为Q.
①在图2中作出四边形PB′C′Q(保留作图痕迹,不必说明作法和理由);
②如果∠C=60°,那么为何值时,B′P⊥AB.
如图,在平面直角坐标系中,直线y=﹣x+m分别与x轴、y轴交于点B、A.其中B点坐标为(12,0),直线y=x与直线AB相交于点C.
(1)求点A的坐标.
(2)求△BOC的面积.
(3)点D为直线AB上的一个动点,过点D作y轴的平行线DE,DE与直线OC交于点E(点D与点E不重合).设点D的横坐标为t,线段DE长度为d.
①求d与t的函数解析式(写出自变量的取值范围).
②当动点D在线段AC上运动时,以DE为边在DE的左侧作正方形DEPQ,若以点H(,t)、G(1,t)为端点的线段与正方形DEPQ的边只有一个交点时,请直接写出t的取值范围.
答案解析
1 、选择题
【考点】常量与变量
【分析】根据函数的定义,可得答案.
解:y=3x﹣1,中y随x的变化而变化,x是自变量,y是x的函数,
故选:D.
【点评】本题考查了自变量,利用函数的定义是解题关键.
【考点】中心对称图形;轴对称图形.
【分析】根据轴对称图形与中心对称图形的概念求解.
解:A.是轴对称图形,不是中心对称图形,符合题意;
B、是轴对称图形,也是中心对称图形,不合题意;
C、是轴对称图形,也是中心对称图形,不合题意;
D、不是轴对称图形,是中心对称图形,不合题意.
故选:A.
【考点】多边形内角与外角.
【分析】设这个多边形的边数为n.根据题意列出方程即可解决问题.
解:设这个多边形的边数为n.
由题意(n﹣2) 180°=2×360°,
解得n=6,
答:这个多边形是正六边形.
故选C.
【点评】本题考查多边形的内角和、外角和等知识,解题的关键是学会构建方程解决问题.
【考点】折线统计图
【分析】先计算出八年级(3)班的全体人数,然后用选择“5G时代”的人数除以八年级(3)班的全体人数即可.
解:由图知,八年级(3)班的全体人数为:(人)
选择“5G时代”的人数为:30人
∴选择“时代”的频率是:
故选:B.
【点评】本题考查了折线统计图的读取,及相应频率的计算,熟知以上知识是解题的关键.
【考点】含30度角的直角三角形.
【分析】根据30°角所对的直角边等于斜边的一半解答即可.
解:∵∠ACB=90°,∠ACD=30°,
∴AD=AC,A错误;
∵∠ACD+∠A=90°,∠B+∠A=90°,
∴∠ACD=∠B=30°,
∴ACAB,B正确;
CD=BC,C、D错误;
故选:B.
【考点】关于x轴、y轴对称的点的坐标.
【分析】关于y轴对称的点,纵坐标相同,横坐标互为相反数,可得答案.
解:P(1,﹣2)关于y轴对称的点的坐标是(﹣1,﹣2),
故选:C.
【点评】本题主要考查的是关于坐标轴对称的点的坐标特点,关于y轴对称点的横坐标互为相反数,纵坐标相等;关于x轴对称点纵坐标互为相反数,横坐标相等.
【考点】勾股定理,含30度角的直角三角形.
【分析】根据勾股定理和含30°角的直角三角形的性质即可得到结论.
解:∵∠OBC=90°,OC=,BC=1,
∴OB===2,
∵∠A=90°,∠AOB=30°,
∴AB=OB=1,
∴OA===,
故选:A.
【点评】本题主要考查了勾股定理,含30°角的直角三角形的性质,三角函数等知识,熟练掌握等角的三角函数值相等是解题的关键.
【考点】一次函数与一元一次不等式.
【分析】首先把点A(2,1)代入y=kx+3中,可得k的值,再解不等式kx+3≥0即可.
解:∵y=kx+3经过点A(2,1),
∴1=2k+3,
解得:k=﹣1,
∴一次函数解析式为:y=﹣x+3,
﹣x+3≥0,
解得:x≤3.
故选A.
【点评】本题考查了一次函数求解析式,以及一元一次不等式的解法,正确求得k的值是关键.
【考点】全等三角形的判定与性质,平行四边形的性质,矩形的判定
【分析】由平行四边形的性质可知:OA=OC,OB=OD,再证明OM=ON即可证明四边形AMCN是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
∵对角线BD上的两点M、N满足BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵OM=AC,
∴MN=AC,
∴四边形AMCN是矩形.
故选:A.
【点评】本题考查了矩形的判定,平行四边形的判定与性质,解题的关键是灵活运用所学知识解决问题.
【考点】代数式求值,一次函数图象上点的坐标特征
【分析】把代入函数解析式得,化简得,化简所求代数式即可得到结果;
解:把代入函数解析式得:,
化简得到:,
∴.
故选:C.
【点评】本题主要考查了通过函数解析式与已知点的坐标得到式子的值,求未知式子的值,准确化简式子是解题的关键.
【考点】规律型:点的坐标
【分析】根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2018除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图,经过6次反弹后动点回到出发点(0,3),
∵2018÷6=336…2,
∴当点P第2018次碰到矩形的边时为第336个循环组的第2次反弹,
点P的坐标为(7,4).
故选:C.
【点评】考查根据图形找出点的坐标变化规律,理解题意,画出示意图,正确总结规律是解题的关键.
【考点】菱形的性质
【分析】根据菱形的对角线互相垂直平分求出OA、OB,再根据勾股定理列式求出AB,然后根据菱形的面积等于底边乘以高,也等于对角线乘积的一半列式计算即可得解.
解:∵菱形ABCD的对角线
根据勾股定理,
设菱形的高为h,
则菱形的面积
即
解得
即菱形的高为cm.
故选B.
【点评】本题考查了菱形的性质,主要利用了菱形的对角线互相垂直平分的性质,以及菱形的面积的两种求解方法.
1 、填空题
【考点】多边形内角与外角.
【分析】设外角为2x,则其内角为3x,根据其内外角互补可以列出方程求得外角的度数,然后利用外角和定理求得边数即可.
解:设外角为2x,则其内角为3x,
则2x+3x=180°,
解得:x=36°,
∴外角为2x=72°,
∵正n边形外角和为360°,
∴n=360°÷72°=5,
故答案为:5.
【点评】本题考查了正多边形的外角与内角的知识,熟练掌握正多边形的内角和和外角和定理是解决此类题目的关键.
【考点】翻折变换(折叠问题);平行四边形的性质.
【分析】由平行四边形的性质和折叠的性质,得出∠ADB=∠BDG=∠DBG,由三角形的外角性质求出∠BDG=∠DBG=∠1=25°,再由三角形内角和定理求出∠A,即可得到结果.
解:∵AD∥BC,
∴∠ADB=∠DBG,
由折叠可得∠ADB=∠BDG,
∴∠DBG=∠BDG,
又∵∠1=∠BDG+∠DBG=50°,
∴∠ADB=∠BDG=25°,
又∵∠2=50°,
∴△ABD中,∠A=105°,
∴∠A'=∠A=105°,
故答案为:105°.
【点评】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质,求出∠BAC的度数是解决问题的关键.
【考点】点的坐标特征
【分析】根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”,再根据各象限内的点的坐标的特点列出不等式组求解即可.
解:∵点P(a+1,2a-4)关于x轴的对称点在第一象限,
∴点P在第四象限,
∴,
解不等式①得,a>-1,
解不等式②得,a<2,
所以,不等式组的解集是-1<a<2.
故答案为-1<a<2.
【点评】本题考查了关于x轴、y轴对称点的坐标,以及各象限内点的坐标的特点,判断出点P在第四象限是解题的关键.
【考点】折线统计图
【分析】(1)由折线统计图可知:离横轴越远的点,表示离家越远,则在E点或F点时该人离家最远,距离为30km;
(2)当距离不增加或减小时,表示此人正在休息,则图中由C到D点,以及由E到F点距离是不变化的,时间一共为30+60=90分钟.
解:(1)30km;
(2)30+60=90分钟
【点评】本题考查的是折线统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.
【考点】待定系数法求一次函数解析式
【分析】根据直线y=kx+b经过两点(3,6)和(﹣1,﹣2),利用待定系数法列式求出k、b的值,从而得解.
解:∵直线y=kx+b经过(3,6)和(﹣1,﹣2)两点, ∴ ,
解得 ,
∴这条直线的解析式为y=2x.
故答案为:y=2x.
【考点】折叠的性质,等边三角形的判定和性质,含300的直角三角形,勾股定理
【分析】①首先根据EF垂直平分AB,可得AN=BN;然后根据折叠的性质,可得AB=BN,据此判断出△ABN为等边三角形,即可判断出∠ABN=60°.
②首先根据∠ABN=60°,∠ABM=∠NBM,求出∠ABM=∠NBM=30°;然后在Rt△ABM中,根据AB=2,求出AM的大小即可.
③首先根据EF∥BC,QN是△MBG的中位线,可得QN=BG;然后根据BG=BM=AB÷cos∠ABM=2÷=,求出QN的长度即可.
④根据∠ABM=∠MBN=30°,∠BNM=∠BAM=90°,推得∠MBG=∠BMG=∠BGM=60°,即可推得△BMG是等边三角形.
⑤首先根据△BMG是等边三角形,点N是MG的中点,判断出BN⊥MG,即可求出BN的大小;然后根据E点和H点关于BM称可得PH=PE,因此P与Q重合时,PN+PH=PN+PE=EN,据此求出PN+PH的最小值是多少即可.
解:如图1,连接AN,
∵EF垂直平分AB,
∴AN=BN,
根据折叠的性质,可得
AB=BN,
∴AN=AB=BN.
∴△ABN为等边三角形.
∴∠ABN=60°,∠PBN=60°÷2=30°,
即结论①正确;
∵∠ABN=60°,∠ABM=∠NBM,
∴∠ABM=∠NBM=60°÷2=30°,
∴AM=AB tan30°=2×=,
即结论②不正确.
∵EF∥BC,QN是△MBG的中位线,
∴QN=QN=BG;
∵BG=BM=AB÷cos∠ABM=2÷=,
∴QN=×=,
即结论③不正确.
∵∠ABM=∠MBN=30°,∠BNM=∠BAM=90°,
∴∠BMG=∠BNM-∠MBN=90°-30°=60°,
∴∠MBG=∠ABG-∠ABM=90°-30°=60°,
∴∠BGM=180°-60°-60°=60°,
∴∠MBG=∠BMG=∠BGM=60°,
∴△BMG为等边三角形,
即结论④正确.
∵△BMG是等边三角形,点N是MG的中点,
∴BN⊥MG,∴BN=BG sin60°=×=2,
根据条件易知E点和H点关于BM对称,∴PH=PE,
∴P与Q重合时,PN+PH的值最小,此时PN+PH=PN+PE=EN,
∵EN=(AM+BG)=(+)=,
∴PN+PH=,
∴PN+PH的最小值是,
即结论⑤正确.
故答案为:①④⑤.
【点评】(1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合方法的应用,要熟练掌握.
(2)此题还考查了等边三角形的判定和性质的应用,以及矩形的性质和应用,要熟练掌握.
(3)此题还考查了折叠的性质和应用,以及余弦定理的应用,要熟练掌握.
1 、解答题
【考点】坐标与图形变化﹣平移.
【分析】根据平面直角坐标系写出各点的坐标即可;
再根据网格结构找出30秒后各大雁的位置,然后根据平面直角坐标系写出各点的坐标,再利用勾股定理列式计算即可求出AA′的长度.
解:A(1,﹣1),B(2,1),C(﹣1,0),D(3,3),E(﹣3,1),F(5,5),G(﹣5,2);
30秒后,这6只大雁的新位置的坐标分别是:
B′(5,﹣3),C′(2,﹣4),D′(6,﹣1),E′(0,﹣3),F′(8,1),G′(﹣2,﹣2),
AA′==5.
【点评】本题考查了坐标与图形变化﹣平移,是基础题,主要利用了在平面直角坐标系中确定点的位置和写出点的坐标.
【考点】全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理
【分析】过点C作CG∥AB交ED的延长线于点G,连接FG,易证△BDE≌△CDG,可得DE=DG,BE=CG,即可求得∠FCG=90°,根据勾股定理可得CG2+CF2=FG2,根据等量代换即可解题.
解:如图,过点C作CG∥AB交ED的延长线于点G,连接FG.
∵CG∥AB,
∴∠B=∠DCG,∠BED=∠DGC.
∵BD=CD,
∴△BDE≌△CDG,(AAS)
∴DE=DG,BE=CG.
∵∠EDF=90°,
∴DF垂直平分EG,
∴EF=FG.
∵∠A=90°,
∴∠B+∠DCF=180°-90°=90°,
∴∠DCF+∠DCG=∠FCG=90°.
在Rt△CFG中,CG2+CF2=FG2,
即BE2+CF2=EF2.
【点评】本题考查了全等三角形的判定与性质,等腰三角形的判定与性质以及勾股定理,作合适的辅助线是解题的关键.
【考点】条形统计图
【分析】(1)根据C组的人数和所占的百分比,可以计算出本次共调查了多少名学生;
(2)根据(1)中的结果可以计算出B组的人数,然后即可补全条形统计图;
(3)根据统计图图中的数据,可以计算出该校学生平均每天睡眠时间不足9h的人数.
解:(1)本次共调查了90÷45%=200(人),
故答案为:200;
(2)B组学生有:200﹣20﹣90﹣30=60(人),
补全的条形统计图如图2所示:
(3)1200×=480(人),
即估计该校学生平均每天睡眠时间不足9h的有480人.
【点评】本题考查的是条形统计图,读懂统计图,会计算部分的数量,根据部分的百分比求总体的数量,从统计图中得到必要的信息是解决问题的关键.
【考点】平行四边形的性质;全等三角形的判定与性质.
【分析】根据平行四边形性质得出AD∥BC,AD=BC,求出DE=BF,DE∥BF,得出四边形DEBF是平行四边形,根据平行四边形的性质推出即可.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF.
【点评】本题考查了平行四边形的性质和判定的应用,注意:平行四边形的对边平行且相等.
【考点】一次函数的应用
【分析】1)根据购买两种树苗所需费用=A种树苗费用+B种树苗费用,即可解答;
(2)根据购买B种树苗的数量少于A种树苗的数量,列出不等式,确定x的取值范围,再根据(1)得出的y与x之间的函数关系式,利用一次函数的增减性结合自变量的取值即可得出更合算的方案.
解:(1)y=-20x+1890;
(2)由题意,知x<21-x.解,得x<10.5.
又∵x≥,∴x的取值范围是:1≤x≤10且x为整数.
由(1)知:对于函数y=-20x+1890,y随x的增大而减小.
∴当x=10时,y有最小值:y最小=-20×10+1890=1690.
所以,使费用最省的方案是购买B种树苗10棵,A种树苗11棵.所需费用为1690元.
【点评】本题主要考查的是一元一次不等式及一次函数的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到关于所求量的等量关系和不等关系.
【考点】一次函数图象与几何变换
【分析】(1) 点,,,根据线段经过平移得到线段,其中点的对应点为点,可得B点先向右平移5个单位,向上平移3个单位可得到点C,所以点A先向右平移5个单位,向上平移3个单位可得到点D, (2)点的对应点为点, 点A对应的点D,所以先向右平移5个单位,向上平移3个单位平移得到线段, (3)
解:(1) 因为点,,,且点的对应点为点,
所以B点先向右平移5个单位,向上平移3个单位可得到点C,
所以点A先向右平移5个单位,向上平移3个单位可得到点D,
(2)因为点的对应点为点, 点A对应的点D,
所以先向右平移5个单位,向上平移3个单位平移得到线段,
(3)设直线AC的解析式为y=kx+b,
将点,代入可得:,解得:,
所以,
令,解得,
所以点F,
所以的面积=.
【点评】本题主要考查点的平移规律和一次函数,以及坐标三角形的面积,解决本题的关键是要熟练掌握点的平移规律和一次函数,以及坐标三角形的面积计算方法.
【考点】四边形综合题
【分析】(1)根据两组对边分别平行的四边形是平行四边形进行判断;(2)①根据轴对称的性质进行作图即可;②先根据折叠得出一些对应边相等,对应角相等,并推导出B′D=B′E,再设AP=a,BP=b,利用解直角三角形将DQ和CQ长用含a的代数式表示出来,最后根据CD=DQ+CQ列出关于a、b的关系式,求得a、b的比值即可.
(1)四边形ABCD是平行四边形
证明:∵在四边形ABCD中,AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠C,
∴∠C+∠B=180°,
∴AB∥CD,
∴四边形ABCD是平行四边形;
(2)①作图如下:
②当AB=AD时,平行四边形ABCD是菱形,
由折叠可得,BP=B′P,CQ=C′Q,BC=B′C′,∠C=∠C′=60°=∠A,
当B′P⊥AB时,由B′P∥C′Q,可得C′Q⊥CD,
∴∠PEA=30°=∠DEB′,∠QDC′=30°=∠B′DE,
∴B′D=B′E,
设AP=a,BP=b,则直角三角形APE中,PE=a,且B′P=b,BC=B′C′=CD=a+b,
∴B′E=b﹣a=B′D,
∴C′D=a+b﹣(b﹣a)=a+a,
∴直角三角形C′QD中,C′Q=a=CQ,DQ=C′Q=a,
∵CD=DQ+CQ=a+b,
∴a+a=a+b,
整理得(+1)a=b,
∴==,即=.
【点评】本题主要考查了平行四边形以及菱形,解题的关键是掌握平行四边形的判定以及菱形的判定与性质.在解题时注意,菱形的四条边都相等,此外在折叠问题中,需要抓住对应边相等,对应角相等这些等量关系,折叠问题的实质是轴对称的性质.
【考点】一次函数综合题
【分析】(1)将点B坐标代入解析式可求直线AB解析式,即可求点A坐标;
(2)联立方程组可求点C坐标,即可求解;
(3)由题意列出不等式组,可求解.
解:(1)∵直线y=﹣x+m与y轴交于点B(12,0),
∴0=﹣×12+m,
∴m=9,
∴直线AB的解析式为:y=﹣x+9,
当x=0时,y=9,
∴点A坐标为(0,9);
(2)由题意可得:,
解得:,
∴点C(8,3),
∴△BOC的面积=×12×3=18;
(3)①如图,
∵点D的横坐标为t,
∴点D(t,﹣t+9),点E(t,t),
当t<8时,d=﹣t+9﹣t=﹣t+9,
当t>8时,d=t+t﹣9=t﹣9;
②∵以点H(,t)、G(1,t)为端点的线段与正方形DEPQ的边只有一个交点,
∴≤t≤1或,
∴≤t≤1或≤t≤.
【点评】本题是一次函数综合题,考查了待定系数法求解析式,三角形的面积公式,不等式组的应用,灵活运用这些性质解决问题是本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版2022-2023学年度下学期八年级期末练习数学试1
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
下列给出的式子中,x是自变量的是( )
A.x=5 B.2x+y=0 C.2y2=4x+3 D.y=3x﹣1
下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
A. B. C. D.
如果一个正多边形的内角和等于外角和2倍,则这个正多边形是( )
A.正方形 B.正五边形 C.正六边形 D.正八边形
为庆祝建党99周年,某校八年级(3)班团支部为了让同学们进一步了解中国科技的发展,给班上同学布置了一项课外作业,从选出的以下五个内容中任选部分内容进行手抄报的制作:、“北斗卫星”:、“时代”;、“智轨快运系统”;、“东风快递”;、“高铁”.统计同学们所选内容的频数,绘制如图所示的折线统计图,则选择“时代”的频率是( )
A.0.25 B.0.3 C.25 D.30
如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∠ACD=30°,那么下列结论正确的是( )
A.AD=CD B.AC=AB C.BD=BC D.CD=AB
点P(1,﹣2)关于y轴对称的点的坐标是( )
A.(1,2) B.(﹣1,2) C.(﹣1,﹣2) D.(﹣2,1)
如图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形OABC.若OC=,BC=1,∠AOB=30°,则OA的值为( )
A. B. C. D.1
直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )
A.x≤3 B.x≥3 C.x≥﹣3 D.x≤0
如图,在平行四边形ABCD中,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )
A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND
点在函数的图像上,则代数式的值等于( )
A. B. C. D.
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2018次碰到矩形的边时,点P的坐标为( )
A.(0,3) B.(5,0) C.(7,4) D.(8,3)
如图,菱形ABCD的对角线交于点O,AC=8cm,BD=6cm,则菱形的高为( )
A. cm B. cm C. cm D. cm
1 、填空题(本大题共6小题,每小题4分,共24分)
如果正n边形的一个内角与一个外角的比是3:2,则n= .
如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点A'处.若∠1=∠2=50°,则∠A'为 .
已知点P(a+1,2a-4)关于x轴的对称点在第一象限,则a的取值范围是_________.
如图,图中折线表示一人骑自行车离家的距离与时间的关系,骑车者九点离开家,十五点到家,根据折线图提供的信息:
(1)该人离家最远距离是 km;
(2)此人总共休息了 分.
已知直线y=kx+b经过两点(3,6)和(﹣1,﹣2),则直线的解析式为________.
如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC 重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.
有如下结论:
1 ∠ABN=600;②AM=1;③QN=;④△BMG是等边三角形; ⑤P为线段BM上
一动点,H是BN的中点,则PN+PH的最小值是.
其中正确结论的序号是 ____________.
1 、解答题(本大题共8小题,共78分)
如图,一群大雁成人字形向南飞去,分别写出它们的坐标,30秒后,领头大雁飞到A′位置,其他大雁B、C、D、E、F、G飞到什么位置?分别写出这6只大雁的新位置的坐标,并计算出AA′的长度.
如图所示,在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,求证:BE2+CF2=EF2.
教育部下发的《关于进一步加强中小学生睡眠管理工作的通知》要求,初中生每天睡眠时间应达到9h.某初中为了解学生每天的睡眠时间,随机调查了部分学生,将学生睡眠时间分为A,B,C,D四组(每名学生必须选择且只能选择一种情况):
A组:睡眠时间<8h
B组:8h≤睡眠时间<9h
C组:9h≤睡眠时间<10h
D组:睡眠时间≥10h
如图1和图2是根据调查结果绘制的不完整的统计图,请根据图中提供的信息,解答下列问题:
(1)被调查的学生有 人;
(2)通过计算补全条形统计图;
(3)请估计全校1200名学生中睡眠时间不足9h的人数.
如图, ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:BE=DF.
为绿化校园,某校计划购进A.B两种树苗,共21棵.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,够买两种树苗所需费用为y元.
(1) y与x的函数关系式为: ;
(2) 若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案.并求出该方案所需费用.
如图,在平面直角坐标系中,点,,,线段经过平移得到线段,其中点的对应点为点,点D在第一象限,直线AC交轴于点
(1)点D坐标为
(2)线段由线段经过怎样平移得到?
(3)求的面积。
如图,在四边形ABCD中,AD∥BC,∠A=∠C,点P在边AB上.
(1)判断四边形ABCD的形状并加以证明;
(2)若AB=AD,以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B′、C′上,且B′C′经过点D,折痕与四边形的另一交点为Q.
①在图2中作出四边形PB′C′Q(保留作图痕迹,不必说明作法和理由);
②如果∠C=60°,那么为何值时,B′P⊥AB.
如图,在平面直角坐标系中,直线y=﹣x+m分别与x轴、y轴交于点B、A.其中B点坐标为(12,0),直线y=x与直线AB相交于点C.
(1)求点A的坐标.
(2)求△BOC的面积.
(3)点D为直线AB上的一个动点,过点D作y轴的平行线DE,DE与直线OC交于点E(点D与点E不重合).设点D的横坐标为t,线段DE长度为d.
①求d与t的函数解析式(写出自变量的取值范围).
②当动点D在线段AC上运动时,以DE为边在DE的左侧作正方形DEPQ,若以点H(,t)、G(1,t)为端点的线段与正方形DEPQ的边只有一个交点时,请直接写出t的取值范围.
答案解析
1 、选择题
【考点】常量与变量
【分析】根据函数的定义,可得答案.
解:y=3x﹣1,中y随x的变化而变化,x是自变量,y是x的函数,
故选:D.
【点评】本题考查了自变量,利用函数的定义是解题关键.
【考点】中心对称图形;轴对称图形.
【分析】根据轴对称图形与中心对称图形的概念求解.
解:A.是轴对称图形,不是中心对称图形,符合题意;
B、是轴对称图形,也是中心对称图形,不合题意;
C、是轴对称图形,也是中心对称图形,不合题意;
D、不是轴对称图形,是中心对称图形,不合题意.
故选:A.
【考点】多边形内角与外角.
【分析】设这个多边形的边数为n.根据题意列出方程即可解决问题.
解:设这个多边形的边数为n.
由题意(n﹣2) 180°=2×360°,
解得n=6,
答:这个多边形是正六边形.
故选C.
【点评】本题考查多边形的内角和、外角和等知识,解题的关键是学会构建方程解决问题.
【考点】折线统计图
【分析】先计算出八年级(3)班的全体人数,然后用选择“5G时代”的人数除以八年级(3)班的全体人数即可.
解:由图知,八年级(3)班的全体人数为:(人)
选择“5G时代”的人数为:30人
∴选择“时代”的频率是:
故选:B.
【点评】本题考查了折线统计图的读取,及相应频率的计算,熟知以上知识是解题的关键.
【考点】含30度角的直角三角形.
【分析】根据30°角所对的直角边等于斜边的一半解答即可.
解:∵∠ACB=90°,∠ACD=30°,
∴AD=AC,A错误;
∵∠ACD+∠A=90°,∠B+∠A=90°,
∴∠ACD=∠B=30°,
∴ACAB,B正确;
CD=BC,C、D错误;
故选:B.
【考点】关于x轴、y轴对称的点的坐标.
【分析】关于y轴对称的点,纵坐标相同,横坐标互为相反数,可得答案.
解:P(1,﹣2)关于y轴对称的点的坐标是(﹣1,﹣2),
故选:C.
【点评】本题主要考查的是关于坐标轴对称的点的坐标特点,关于y轴对称点的横坐标互为相反数,纵坐标相等;关于x轴对称点纵坐标互为相反数,横坐标相等.
【考点】勾股定理,含30度角的直角三角形.
【分析】根据勾股定理和含30°角的直角三角形的性质即可得到结论.
解:∵∠OBC=90°,OC=,BC=1,
∴OB===2,
∵∠A=90°,∠AOB=30°,
∴AB=OB=1,
∴OA===,
故选:A.
【点评】本题主要考查了勾股定理,含30°角的直角三角形的性质,三角函数等知识,熟练掌握等角的三角函数值相等是解题的关键.
【考点】一次函数与一元一次不等式.
【分析】首先把点A(2,1)代入y=kx+3中,可得k的值,再解不等式kx+3≥0即可.
解:∵y=kx+3经过点A(2,1),
∴1=2k+3,
解得:k=﹣1,
∴一次函数解析式为:y=﹣x+3,
﹣x+3≥0,
解得:x≤3.
故选A.
【点评】本题考查了一次函数求解析式,以及一元一次不等式的解法,正确求得k的值是关键.
【考点】全等三角形的判定与性质,平行四边形的性质,矩形的判定
【分析】由平行四边形的性质可知:OA=OC,OB=OD,再证明OM=ON即可证明四边形AMCN是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
∵对角线BD上的两点M、N满足BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵OM=AC,
∴MN=AC,
∴四边形AMCN是矩形.
故选:A.
【点评】本题考查了矩形的判定,平行四边形的判定与性质,解题的关键是灵活运用所学知识解决问题.
【考点】代数式求值,一次函数图象上点的坐标特征
【分析】把代入函数解析式得,化简得,化简所求代数式即可得到结果;
解:把代入函数解析式得:,
化简得到:,
∴.
故选:C.
【点评】本题主要考查了通过函数解析式与已知点的坐标得到式子的值,求未知式子的值,准确化简式子是解题的关键.
【考点】规律型:点的坐标
【分析】根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2018除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图,经过6次反弹后动点回到出发点(0,3),
∵2018÷6=336…2,
∴当点P第2018次碰到矩形的边时为第336个循环组的第2次反弹,
点P的坐标为(7,4).
故选:C.
【点评】考查根据图形找出点的坐标变化规律,理解题意,画出示意图,正确总结规律是解题的关键.
【考点】菱形的性质
【分析】根据菱形的对角线互相垂直平分求出OA、OB,再根据勾股定理列式求出AB,然后根据菱形的面积等于底边乘以高,也等于对角线乘积的一半列式计算即可得解.
解:∵菱形ABCD的对角线
根据勾股定理,
设菱形的高为h,
则菱形的面积
即
解得
即菱形的高为cm.
故选B.
【点评】本题考查了菱形的性质,主要利用了菱形的对角线互相垂直平分的性质,以及菱形的面积的两种求解方法.
1 、填空题
【考点】多边形内角与外角.
【分析】设外角为2x,则其内角为3x,根据其内外角互补可以列出方程求得外角的度数,然后利用外角和定理求得边数即可.
解:设外角为2x,则其内角为3x,
则2x+3x=180°,
解得:x=36°,
∴外角为2x=72°,
∵正n边形外角和为360°,
∴n=360°÷72°=5,
故答案为:5.
【点评】本题考查了正多边形的外角与内角的知识,熟练掌握正多边形的内角和和外角和定理是解决此类题目的关键.
【考点】翻折变换(折叠问题);平行四边形的性质.
【分析】由平行四边形的性质和折叠的性质,得出∠ADB=∠BDG=∠DBG,由三角形的外角性质求出∠BDG=∠DBG=∠1=25°,再由三角形内角和定理求出∠A,即可得到结果.
解:∵AD∥BC,
∴∠ADB=∠DBG,
由折叠可得∠ADB=∠BDG,
∴∠DBG=∠BDG,
又∵∠1=∠BDG+∠DBG=50°,
∴∠ADB=∠BDG=25°,
又∵∠2=50°,
∴△ABD中,∠A=105°,
∴∠A'=∠A=105°,
故答案为:105°.
【点评】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质,求出∠BAC的度数是解决问题的关键.
【考点】点的坐标特征
【分析】根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”,再根据各象限内的点的坐标的特点列出不等式组求解即可.
解:∵点P(a+1,2a-4)关于x轴的对称点在第一象限,
∴点P在第四象限,
∴,
解不等式①得,a>-1,
解不等式②得,a<2,
所以,不等式组的解集是-1<a<2.
故答案为-1<a<2.
【点评】本题考查了关于x轴、y轴对称点的坐标,以及各象限内点的坐标的特点,判断出点P在第四象限是解题的关键.
【考点】折线统计图
【分析】(1)由折线统计图可知:离横轴越远的点,表示离家越远,则在E点或F点时该人离家最远,距离为30km;
(2)当距离不增加或减小时,表示此人正在休息,则图中由C到D点,以及由E到F点距离是不变化的,时间一共为30+60=90分钟.
解:(1)30km;
(2)30+60=90分钟
【点评】本题考查的是折线统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.
【考点】待定系数法求一次函数解析式
【分析】根据直线y=kx+b经过两点(3,6)和(﹣1,﹣2),利用待定系数法列式求出k、b的值,从而得解.
解:∵直线y=kx+b经过(3,6)和(﹣1,﹣2)两点, ∴ ,
解得 ,
∴这条直线的解析式为y=2x.
故答案为:y=2x.
【考点】折叠的性质,等边三角形的判定和性质,含300的直角三角形,勾股定理
【分析】①首先根据EF垂直平分AB,可得AN=BN;然后根据折叠的性质,可得AB=BN,据此判断出△ABN为等边三角形,即可判断出∠ABN=60°.
②首先根据∠ABN=60°,∠ABM=∠NBM,求出∠ABM=∠NBM=30°;然后在Rt△ABM中,根据AB=2,求出AM的大小即可.
③首先根据EF∥BC,QN是△MBG的中位线,可得QN=BG;然后根据BG=BM=AB÷cos∠ABM=2÷=,求出QN的长度即可.
④根据∠ABM=∠MBN=30°,∠BNM=∠BAM=90°,推得∠MBG=∠BMG=∠BGM=60°,即可推得△BMG是等边三角形.
⑤首先根据△BMG是等边三角形,点N是MG的中点,判断出BN⊥MG,即可求出BN的大小;然后根据E点和H点关于BM称可得PH=PE,因此P与Q重合时,PN+PH=PN+PE=EN,据此求出PN+PH的最小值是多少即可.
解:如图1,连接AN,
∵EF垂直平分AB,
∴AN=BN,
根据折叠的性质,可得
AB=BN,
∴AN=AB=BN.
∴△ABN为等边三角形.
∴∠ABN=60°,∠PBN=60°÷2=30°,
即结论①正确;
∵∠ABN=60°,∠ABM=∠NBM,
∴∠ABM=∠NBM=60°÷2=30°,
∴AM=AB tan30°=2×=,
即结论②不正确.
∵EF∥BC,QN是△MBG的中位线,
∴QN=QN=BG;
∵BG=BM=AB÷cos∠ABM=2÷=,
∴QN=×=,
即结论③不正确.
∵∠ABM=∠MBN=30°,∠BNM=∠BAM=90°,
∴∠BMG=∠BNM-∠MBN=90°-30°=60°,
∴∠MBG=∠ABG-∠ABM=90°-30°=60°,
∴∠BGM=180°-60°-60°=60°,
∴∠MBG=∠BMG=∠BGM=60°,
∴△BMG为等边三角形,
即结论④正确.
∵△BMG是等边三角形,点N是MG的中点,
∴BN⊥MG,∴BN=BG sin60°=×=2,
根据条件易知E点和H点关于BM对称,∴PH=PE,
∴P与Q重合时,PN+PH的值最小,此时PN+PH=PN+PE=EN,
∵EN=(AM+BG)=(+)=,
∴PN+PH=,
∴PN+PH的最小值是,
即结论⑤正确.
故答案为:①④⑤.
【点评】(1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合方法的应用,要熟练掌握.
(2)此题还考查了等边三角形的判定和性质的应用,以及矩形的性质和应用,要熟练掌握.
(3)此题还考查了折叠的性质和应用,以及余弦定理的应用,要熟练掌握.
1 、解答题
【考点】坐标与图形变化﹣平移.
【分析】根据平面直角坐标系写出各点的坐标即可;
再根据网格结构找出30秒后各大雁的位置,然后根据平面直角坐标系写出各点的坐标,再利用勾股定理列式计算即可求出AA′的长度.
解:A(1,﹣1),B(2,1),C(﹣1,0),D(3,3),E(﹣3,1),F(5,5),G(﹣5,2);
30秒后,这6只大雁的新位置的坐标分别是:
B′(5,﹣3),C′(2,﹣4),D′(6,﹣1),E′(0,﹣3),F′(8,1),G′(﹣2,﹣2),
AA′==5.
【点评】本题考查了坐标与图形变化﹣平移,是基础题,主要利用了在平面直角坐标系中确定点的位置和写出点的坐标.
【考点】全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理
【分析】过点C作CG∥AB交ED的延长线于点G,连接FG,易证△BDE≌△CDG,可得DE=DG,BE=CG,即可求得∠FCG=90°,根据勾股定理可得CG2+CF2=FG2,根据等量代换即可解题.
解:如图,过点C作CG∥AB交ED的延长线于点G,连接FG.
∵CG∥AB,
∴∠B=∠DCG,∠BED=∠DGC.
∵BD=CD,
∴△BDE≌△CDG,(AAS)
∴DE=DG,BE=CG.
∵∠EDF=90°,
∴DF垂直平分EG,
∴EF=FG.
∵∠A=90°,
∴∠B+∠DCF=180°-90°=90°,
∴∠DCF+∠DCG=∠FCG=90°.
在Rt△CFG中,CG2+CF2=FG2,
即BE2+CF2=EF2.
【点评】本题考查了全等三角形的判定与性质,等腰三角形的判定与性质以及勾股定理,作合适的辅助线是解题的关键.
【考点】条形统计图
【分析】(1)根据C组的人数和所占的百分比,可以计算出本次共调查了多少名学生;
(2)根据(1)中的结果可以计算出B组的人数,然后即可补全条形统计图;
(3)根据统计图图中的数据,可以计算出该校学生平均每天睡眠时间不足9h的人数.
解:(1)本次共调查了90÷45%=200(人),
故答案为:200;
(2)B组学生有:200﹣20﹣90﹣30=60(人),
补全的条形统计图如图2所示:
(3)1200×=480(人),
即估计该校学生平均每天睡眠时间不足9h的有480人.
【点评】本题考查的是条形统计图,读懂统计图,会计算部分的数量,根据部分的百分比求总体的数量,从统计图中得到必要的信息是解决问题的关键.
【考点】平行四边形的性质;全等三角形的判定与性质.
【分析】根据平行四边形性质得出AD∥BC,AD=BC,求出DE=BF,DE∥BF,得出四边形DEBF是平行四边形,根据平行四边形的性质推出即可.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF.
【点评】本题考查了平行四边形的性质和判定的应用,注意:平行四边形的对边平行且相等.
【考点】一次函数的应用
【分析】1)根据购买两种树苗所需费用=A种树苗费用+B种树苗费用,即可解答;
(2)根据购买B种树苗的数量少于A种树苗的数量,列出不等式,确定x的取值范围,再根据(1)得出的y与x之间的函数关系式,利用一次函数的增减性结合自变量的取值即可得出更合算的方案.
解:(1)y=-20x+1890;
(2)由题意,知x<21-x.解,得x<10.5.
又∵x≥,∴x的取值范围是:1≤x≤10且x为整数.
由(1)知:对于函数y=-20x+1890,y随x的增大而减小.
∴当x=10时,y有最小值:y最小=-20×10+1890=1690.
所以,使费用最省的方案是购买B种树苗10棵,A种树苗11棵.所需费用为1690元.
【点评】本题主要考查的是一元一次不等式及一次函数的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到关于所求量的等量关系和不等关系.
【考点】一次函数图象与几何变换
【分析】(1) 点,,,根据线段经过平移得到线段,其中点的对应点为点,可得B点先向右平移5个单位,向上平移3个单位可得到点C,所以点A先向右平移5个单位,向上平移3个单位可得到点D, (2)点的对应点为点, 点A对应的点D,所以先向右平移5个单位,向上平移3个单位平移得到线段, (3)
解:(1) 因为点,,,且点的对应点为点,
所以B点先向右平移5个单位,向上平移3个单位可得到点C,
所以点A先向右平移5个单位,向上平移3个单位可得到点D,
(2)因为点的对应点为点, 点A对应的点D,
所以先向右平移5个单位,向上平移3个单位平移得到线段,
(3)设直线AC的解析式为y=kx+b,
将点,代入可得:,解得:,
所以,
令,解得,
所以点F,
所以的面积=.
【点评】本题主要考查点的平移规律和一次函数,以及坐标三角形的面积,解决本题的关键是要熟练掌握点的平移规律和一次函数,以及坐标三角形的面积计算方法.
【考点】四边形综合题
【分析】(1)根据两组对边分别平行的四边形是平行四边形进行判断;(2)①根据轴对称的性质进行作图即可;②先根据折叠得出一些对应边相等,对应角相等,并推导出B′D=B′E,再设AP=a,BP=b,利用解直角三角形将DQ和CQ长用含a的代数式表示出来,最后根据CD=DQ+CQ列出关于a、b的关系式,求得a、b的比值即可.
(1)四边形ABCD是平行四边形
证明:∵在四边形ABCD中,AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠C,
∴∠C+∠B=180°,
∴AB∥CD,
∴四边形ABCD是平行四边形;
(2)①作图如下:
②当AB=AD时,平行四边形ABCD是菱形,
由折叠可得,BP=B′P,CQ=C′Q,BC=B′C′,∠C=∠C′=60°=∠A,
当B′P⊥AB时,由B′P∥C′Q,可得C′Q⊥CD,
∴∠PEA=30°=∠DEB′,∠QDC′=30°=∠B′DE,
∴B′D=B′E,
设AP=a,BP=b,则直角三角形APE中,PE=a,且B′P=b,BC=B′C′=CD=a+b,
∴B′E=b﹣a=B′D,
∴C′D=a+b﹣(b﹣a)=a+a,
∴直角三角形C′QD中,C′Q=a=CQ,DQ=C′Q=a,
∵CD=DQ+CQ=a+b,
∴a+a=a+b,
整理得(+1)a=b,
∴==,即=.
【点评】本题主要考查了平行四边形以及菱形,解题的关键是掌握平行四边形的判定以及菱形的判定与性质.在解题时注意,菱形的四条边都相等,此外在折叠问题中,需要抓住对应边相等,对应角相等这些等量关系,折叠问题的实质是轴对称的性质.
【考点】一次函数综合题
【分析】(1)将点B坐标代入解析式可求直线AB解析式,即可求点A坐标;
(2)联立方程组可求点C坐标,即可求解;
(3)由题意列出不等式组,可求解.
解:(1)∵直线y=﹣x+m与y轴交于点B(12,0),
∴0=﹣×12+m,
∴m=9,
∴直线AB的解析式为:y=﹣x+9,
当x=0时,y=9,
∴点A坐标为(0,9);
(2)由题意可得:,
解得:,
∴点C(8,3),
∴△BOC的面积=×12×3=18;
(3)①如图,
∵点D的横坐标为t,
∴点D(t,﹣t+9),点E(t,t),
当t<8时,d=﹣t+9﹣t=﹣t+9,
当t>8时,d=t+t﹣9=t﹣9;
②∵以点H(,t)、G(1,t)为端点的线段与正方形DEPQ的边只有一个交点,
∴≤t≤1或,
∴≤t≤1或≤t≤.
【点评】本题是一次函数综合题,考查了待定系数法求解析式,三角形的面积公式,不等式组的应用,灵活运用这些性质解决问题是本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
