广东省2023年中考数学模拟预测卷(3)(无答案)
文档属性
| 名称 | 广东省2023年中考数学模拟预测卷(3)(无答案) | 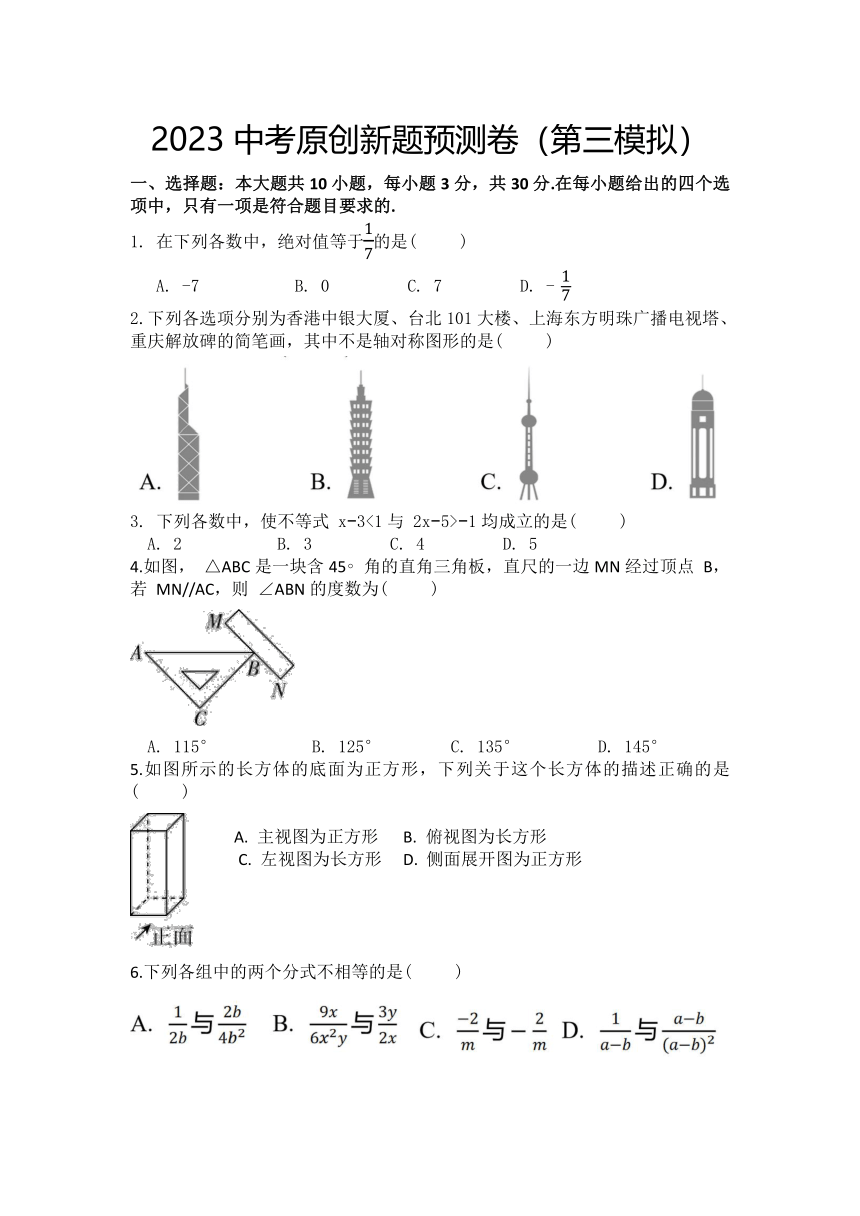 | |
| 格式 | docx | ||
| 文件大小 | 419.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-10 20:30:42 | ||
图片预览



文档简介
2023中考原创新题预测卷(第三模拟)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 在下列各数中,绝对值等于的是( )
A. -7 B. 0 C. 7 D. -
2.下列各选项分别为香港中银大厦、台北101大楼、上海东方明珠广播电视塔、重庆解放碑的简笔画,其中不是轴对称图形的是( )
3. 下列各数中,使不等式 x 3<1与 2x 5> 1均成立的是( )
A. 2 B. 3 C. 4 D. 5
4.如图, △ABC是一块含45 角的直角三角板,直尺的一边MN经过顶点 B,若 MN//AC,则 ∠ABN的度数为( )
A. 115° B. 125° C. 135° D. 145°
5.如图所示的长方体的底面为正方形,下列关于这个长方体的描述正确的是( )
主视图为正方形 B. 俯视图为长方形
C. 左视图为长方形 D. 侧面展开图为正方形
6.下列各组中的两个分式不相等的是( )
7. 对于许多植物来说,叶子从中轴附近生长出来,为了在生长过程中一直能够最佳地利用空间,每片叶子和前一片叶子会形成一个最佳角度,这个角度与圆周 360 的比值约为0.618,因此它被称为“黄金角度”,则“黄金角度”的度数约为( )
A. 222.48 B. 232.48 C. 242.68 D. 252.68
8. 如图,△ACB和△ACD均为 ⊙O的内接三角形,且 AB为直径,若 ∠D=70 ,则 ∠CAB的度数是( )
A. 15° B. 20° C. 25° D. 30°
9.中国邮政推出了2023年“癸卯贺春”贺年明信片,该套明信片采用平面插画的方式表现了新春佳节中国传统民俗活动,画风时尚灵动,造型活泼可爱.小明购买了一套(共4张)明信片,主题分别为“耍龙灯”“舞醒狮”“游锣鼓”“赏花灯”(如图),他打算送两张给同桌小亮.小明洗匀后将它们背面朝上放到桌面上(明信片背面完全一样),让小亮随机抽取两张,则小亮抽到的两张明信
片恰好是“耍龙灯”和“舞醒狮”的概率是( )
A. B. C. D.
10.如图,反比例函数 y=(x>0)的图象与直线y=k(x 3)+4(k<0)交于 A, B两点,其中点B的横坐标大于3,连接OA,OB,当△AOB的面积为9时,k的值为( )
A. B. C. D.
二、填空题:本大题共5小题,每小题3分,共15分.
11. 因式分解: 49 a2= .
12. 北京时间2022年11月21日零时,2022年卡塔尔世界杯比赛正式开始.作为中国建造的主体育场—卢赛尔球场,引发了全球瞩目.卢赛尔球场建筑面积达19.5万平方米,可容纳8万人同时观赛.其中数据19.5万用科学记数法表示为 .
13. 在平面直角坐标系中,点 A(3,2)向下平移4个单位长度得到点B,点 B关于原点对称的点为C,则点C的坐标为 .
14. 一个多边形的每个外角都等于其相邻内角的,则这个多边形的边数为_________.
如图,在△ABC中, ∠ACB=60 ,AC=4,BC=7,点D为AC的中点,点E为BC上一点,连接DE,作点C关于直线DE的对称点C′,连接DC′,EC′, BC′.若四边形 CDC′E为平行四边形,则 BC′的长为__________.
三、解答题(一):本大题共3小题,每小题 8分,共24分.
16.解二元一次方程组:
17.“坡道定点停车和起步”是小型汽车(C1)驾照考试科目二(场地驾驶技能)的必考项目.如图为某驾校供学员训练该项目使用的斜坡的抽象截面图,学员在斜坡 AB段完成“起步→定点停车→起步”的过程,再从斜坡BC段下坡离场,其中斜坡 AB的坡度i=tan A=1/8, ∠C=30°,BH⊥AC于点H,BH=4米,求斜坡坡面(折线 ABC)的总长度.(结果精确到0.1米,≈8.06)
如图,在 Rt△ABC中, ∠ABC=90 .
(1)作出斜边AC的垂直平分线,垂足为O,连接BO并延长到点D,使得OD=OB,连接 AD,CD(要求:尺规作图,保留作图痕迹,不写作法,标明字母);
(2)在(1)的条件下,试猜想四边形 ABCD的形状,并加以证明.
四、解答题(二):本大题共3小题,每小题 9分,共27分.
19.广东绿道建设起步早、历时长、成效快,现已形成了遍布南粤大地的绿道网络,将居民点、自然和人文景观与生态保护地串联为一体.小张和小李相约到某体育休闲公园的环湖绿道上匀速骑行,已知环湖绿道全长6 600米,小张的速度是小李的速度的1.2倍.
(1)若两人同时出发,背向而行,经过12分钟后两人相遇,则小李每分钟骑行多少米?
(2)若两人同时出发,同向而行,最终小张比小李早了4分钟回到起点,则小李每分钟骑行多少米?
20.经有关方面协商一致,并经亚奥理事会执委会批准,杭州2022年第19届亚运会将于2023年9月23日至10月8日举行.为迎接亚运会的到来,某校组织了体育知识竞赛活动,现从男生和女生中各随机选出10名参赛学生的成绩进行分析,将学生竞赛成绩(满分100分)分为优、良、中、差四个等级(优:
90≤x≤100,良:80≤x<90,中:70≤x<80,差:0≤x<70).
10名女生的竞赛成绩为:67,77,80,85,87,87,87,88,94,99.
男生竞赛成绩的条形统计图如下所示,其中成绩等级为良的是:85,86,86,86,88.
两组数据的平均数、中位数、众数、方差如下表所示:
男生竞赛成绩条形统计图
根据以上信息,解答下列问题.
(1)填空:a= ,b= .
(2)补全条形统计图.
(3)根据以上数据,你认为在此次知识竞赛中,男生还是女生的竞赛成绩更好?请说明理由.(一条理由即可)
21.已知关于x的一元二次方程 ax2+bx+c=0(a,b,c为常数,且 a≠0).
(1)若 b=2a,c= 3a,求方程的根;
(2)若 b=3a+c,求证:该方程总有两个不相等的实数根.
五、解答题(三):本大题共2小题,每小题12分,共24分.
22.如图(1)为一个圆形喷水池,水池的中心 O处有一喷水装置,数学活动小组计划使用皮尺测量水池的直径,但因喷水装置阻挡,所以无法直接测量,需要如何进行呢?(水池边缘厚度忽略不计)
图(1) 图(2) 图(3) 图(4)
【方案解决】同学们设计了如下两种方案:
方案一:如图(2),先在水池边上取A,B两点,使得A,O,B三点共线,再在水池外取一点 C,测得 AC, BC的长,在射线AC, BC上分别取点D,E,使得CD=AC,CE=BC,最后测得 DE的长,便可求出 AB的长;
方案二:如图(3),先在水池边上取A,B两点,使得A,O,B 三点共线,再在水池外取一点 C,测得AC,BC的长,在射线AC , BC上分别取点D,E,使得CD=AC, CE= BC,最后测得DE的长,便可求出AB的长.
①理论上,方案一是否可行?请说明理由.
②理论上,方案二是否可行?请说明理由.
(2)同学们去实地考察后,发现喷水装置较大,阻挡视线,难以保障 A, O,B三点共线,经过讨论,同学们设计并实施了方案三:如图(4),在水池边上取三点 A,B,C,使得AB=AC,测得 AB , AC , BC的长,通过计算,便可求得圆形水池的直径.若测得AB=AC=12米,BC=8米,请根据测量的数据,求出水池的直径.
抛物线y=x2+(m 2)x+m 3与 x轴交于点A,B(点A在点B左侧),与y轴交于点C,点P是抛物线上一点,其横坐标为a.
(1)若点A,B均位于x轴负半轴,求m的取值范围.
(2)若m=-1.
①当点P在x轴上方时,直接写出a的取值范围;
②如图,当点P位于第四象限时,过点P分别作直线BC,y轴的垂线PE, PF,垂足分别为E , F,若PE+PF取得最大值,求a的值.
③在②的条件下,连接PB,PC,此时△PBC的面积是否最大?请说明理由.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 在下列各数中,绝对值等于的是( )
A. -7 B. 0 C. 7 D. -
2.下列各选项分别为香港中银大厦、台北101大楼、上海东方明珠广播电视塔、重庆解放碑的简笔画,其中不是轴对称图形的是( )
3. 下列各数中,使不等式 x 3<1与 2x 5> 1均成立的是( )
A. 2 B. 3 C. 4 D. 5
4.如图, △ABC是一块含45 角的直角三角板,直尺的一边MN经过顶点 B,若 MN//AC,则 ∠ABN的度数为( )
A. 115° B. 125° C. 135° D. 145°
5.如图所示的长方体的底面为正方形,下列关于这个长方体的描述正确的是( )
主视图为正方形 B. 俯视图为长方形
C. 左视图为长方形 D. 侧面展开图为正方形
6.下列各组中的两个分式不相等的是( )
7. 对于许多植物来说,叶子从中轴附近生长出来,为了在生长过程中一直能够最佳地利用空间,每片叶子和前一片叶子会形成一个最佳角度,这个角度与圆周 360 的比值约为0.618,因此它被称为“黄金角度”,则“黄金角度”的度数约为( )
A. 222.48 B. 232.48 C. 242.68 D. 252.68
8. 如图,△ACB和△ACD均为 ⊙O的内接三角形,且 AB为直径,若 ∠D=70 ,则 ∠CAB的度数是( )
A. 15° B. 20° C. 25° D. 30°
9.中国邮政推出了2023年“癸卯贺春”贺年明信片,该套明信片采用平面插画的方式表现了新春佳节中国传统民俗活动,画风时尚灵动,造型活泼可爱.小明购买了一套(共4张)明信片,主题分别为“耍龙灯”“舞醒狮”“游锣鼓”“赏花灯”(如图),他打算送两张给同桌小亮.小明洗匀后将它们背面朝上放到桌面上(明信片背面完全一样),让小亮随机抽取两张,则小亮抽到的两张明信
片恰好是“耍龙灯”和“舞醒狮”的概率是( )
A. B. C. D.
10.如图,反比例函数 y=(x>0)的图象与直线y=k(x 3)+4(k<0)交于 A, B两点,其中点B的横坐标大于3,连接OA,OB,当△AOB的面积为9时,k的值为( )
A. B. C. D.
二、填空题:本大题共5小题,每小题3分,共15分.
11. 因式分解: 49 a2= .
12. 北京时间2022年11月21日零时,2022年卡塔尔世界杯比赛正式开始.作为中国建造的主体育场—卢赛尔球场,引发了全球瞩目.卢赛尔球场建筑面积达19.5万平方米,可容纳8万人同时观赛.其中数据19.5万用科学记数法表示为 .
13. 在平面直角坐标系中,点 A(3,2)向下平移4个单位长度得到点B,点 B关于原点对称的点为C,则点C的坐标为 .
14. 一个多边形的每个外角都等于其相邻内角的,则这个多边形的边数为_________.
如图,在△ABC中, ∠ACB=60 ,AC=4,BC=7,点D为AC的中点,点E为BC上一点,连接DE,作点C关于直线DE的对称点C′,连接DC′,EC′, BC′.若四边形 CDC′E为平行四边形,则 BC′的长为__________.
三、解答题(一):本大题共3小题,每小题 8分,共24分.
16.解二元一次方程组:
17.“坡道定点停车和起步”是小型汽车(C1)驾照考试科目二(场地驾驶技能)的必考项目.如图为某驾校供学员训练该项目使用的斜坡的抽象截面图,学员在斜坡 AB段完成“起步→定点停车→起步”的过程,再从斜坡BC段下坡离场,其中斜坡 AB的坡度i=tan A=1/8, ∠C=30°,BH⊥AC于点H,BH=4米,求斜坡坡面(折线 ABC)的总长度.(结果精确到0.1米,≈8.06)
如图,在 Rt△ABC中, ∠ABC=90 .
(1)作出斜边AC的垂直平分线,垂足为O,连接BO并延长到点D,使得OD=OB,连接 AD,CD(要求:尺规作图,保留作图痕迹,不写作法,标明字母);
(2)在(1)的条件下,试猜想四边形 ABCD的形状,并加以证明.
四、解答题(二):本大题共3小题,每小题 9分,共27分.
19.广东绿道建设起步早、历时长、成效快,现已形成了遍布南粤大地的绿道网络,将居民点、自然和人文景观与生态保护地串联为一体.小张和小李相约到某体育休闲公园的环湖绿道上匀速骑行,已知环湖绿道全长6 600米,小张的速度是小李的速度的1.2倍.
(1)若两人同时出发,背向而行,经过12分钟后两人相遇,则小李每分钟骑行多少米?
(2)若两人同时出发,同向而行,最终小张比小李早了4分钟回到起点,则小李每分钟骑行多少米?
20.经有关方面协商一致,并经亚奥理事会执委会批准,杭州2022年第19届亚运会将于2023年9月23日至10月8日举行.为迎接亚运会的到来,某校组织了体育知识竞赛活动,现从男生和女生中各随机选出10名参赛学生的成绩进行分析,将学生竞赛成绩(满分100分)分为优、良、中、差四个等级(优:
90≤x≤100,良:80≤x<90,中:70≤x<80,差:0≤x<70).
10名女生的竞赛成绩为:67,77,80,85,87,87,87,88,94,99.
男生竞赛成绩的条形统计图如下所示,其中成绩等级为良的是:85,86,86,86,88.
两组数据的平均数、中位数、众数、方差如下表所示:
男生竞赛成绩条形统计图
根据以上信息,解答下列问题.
(1)填空:a= ,b= .
(2)补全条形统计图.
(3)根据以上数据,你认为在此次知识竞赛中,男生还是女生的竞赛成绩更好?请说明理由.(一条理由即可)
21.已知关于x的一元二次方程 ax2+bx+c=0(a,b,c为常数,且 a≠0).
(1)若 b=2a,c= 3a,求方程的根;
(2)若 b=3a+c,求证:该方程总有两个不相等的实数根.
五、解答题(三):本大题共2小题,每小题12分,共24分.
22.如图(1)为一个圆形喷水池,水池的中心 O处有一喷水装置,数学活动小组计划使用皮尺测量水池的直径,但因喷水装置阻挡,所以无法直接测量,需要如何进行呢?(水池边缘厚度忽略不计)
图(1) 图(2) 图(3) 图(4)
【方案解决】同学们设计了如下两种方案:
方案一:如图(2),先在水池边上取A,B两点,使得A,O,B三点共线,再在水池外取一点 C,测得 AC, BC的长,在射线AC, BC上分别取点D,E,使得CD=AC,CE=BC,最后测得 DE的长,便可求出 AB的长;
方案二:如图(3),先在水池边上取A,B两点,使得A,O,B 三点共线,再在水池外取一点 C,测得AC,BC的长,在射线AC , BC上分别取点D,E,使得CD=AC, CE= BC,最后测得DE的长,便可求出AB的长.
①理论上,方案一是否可行?请说明理由.
②理论上,方案二是否可行?请说明理由.
(2)同学们去实地考察后,发现喷水装置较大,阻挡视线,难以保障 A, O,B三点共线,经过讨论,同学们设计并实施了方案三:如图(4),在水池边上取三点 A,B,C,使得AB=AC,测得 AB , AC , BC的长,通过计算,便可求得圆形水池的直径.若测得AB=AC=12米,BC=8米,请根据测量的数据,求出水池的直径.
抛物线y=x2+(m 2)x+m 3与 x轴交于点A,B(点A在点B左侧),与y轴交于点C,点P是抛物线上一点,其横坐标为a.
(1)若点A,B均位于x轴负半轴,求m的取值范围.
(2)若m=-1.
①当点P在x轴上方时,直接写出a的取值范围;
②如图,当点P位于第四象限时,过点P分别作直线BC,y轴的垂线PE, PF,垂足分别为E , F,若PE+PF取得最大值,求a的值.
③在②的条件下,连接PB,PC,此时△PBC的面积是否最大?请说明理由.
同课章节目录
