数轴授课课件
图片预览




文档简介
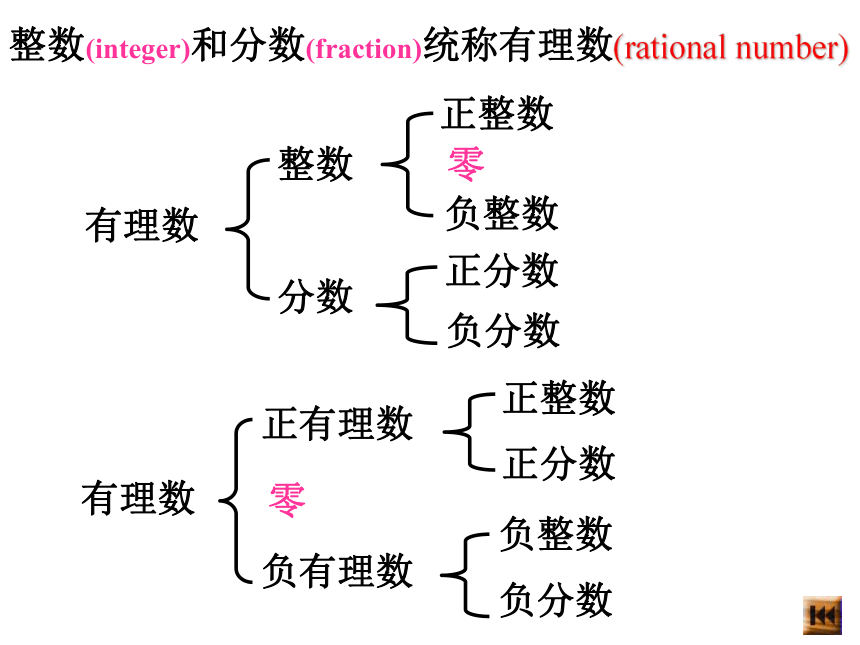
课件24张PPT。人教版初中数学七年级上册1.2.2 数轴整数(integer)和分数(fraction)统称有理数(rational number)有理数整数
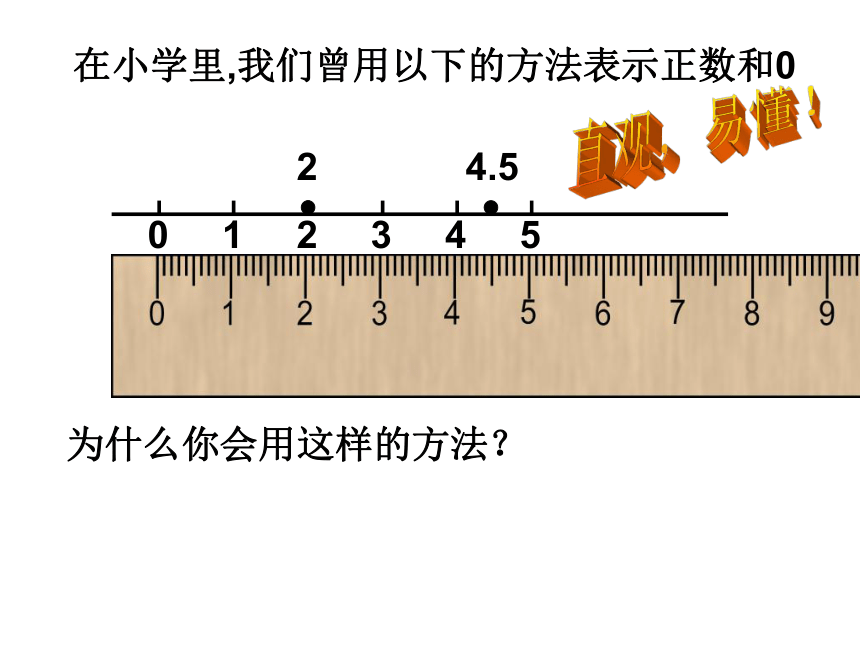
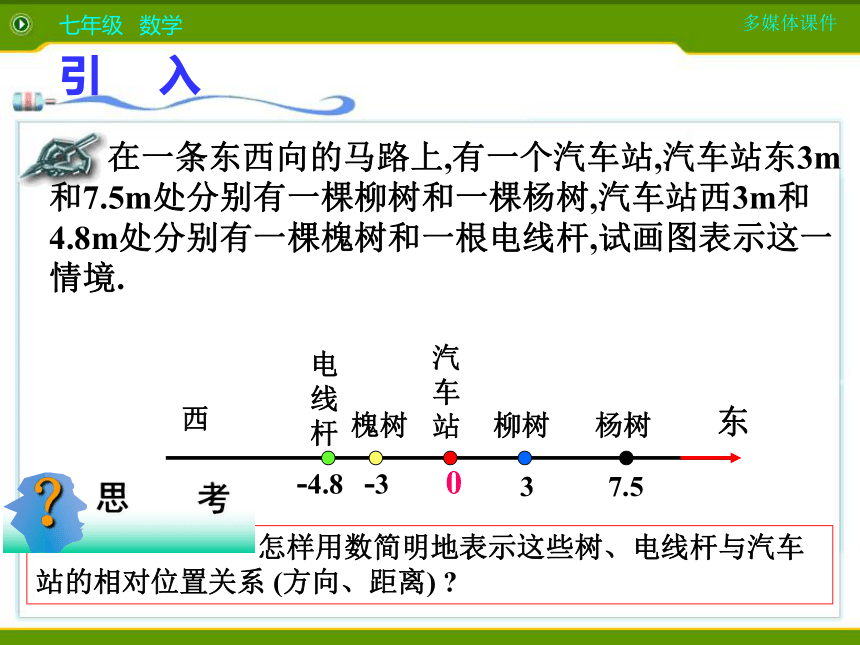
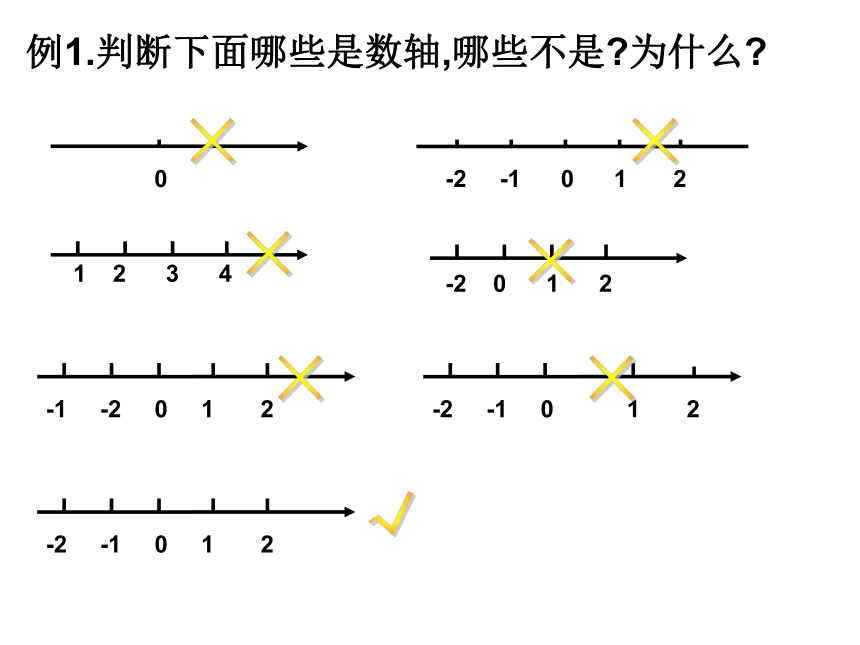
分数正整数 零负整数正分数负分数有理数正有理数零负有理数正整数正分数负整数负分数在小学里,我们曾用以下的方法表示正数和0为什么你会用这样的方法?直观,易懂! 古代部落酋长上任时先在绳上打了个红绳结表示财物往来从0开始,如捕获一只羊在红绳结右边顺次打一个结,每向其他部落借出一只羊就在红绳结左边顺次打一个结,你能解读如图所示A、B绳结的含义吗? 穿越时空 B (左)红绳结(右) A 在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.引入37.5-3-4.8东西汽车站柳树杨树槐树电线杆0活动2学习数轴概念:一般地,在数学中人们用画图把数“直观化”。通常用一条直线上的点表示数,这条直线叫做数轴.教师讲解、学生理解(1)在直线上任取一个点表示数0,这个点叫做原点;(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法表示-1,-2,-3,…例1.判断下面哪些是数轴,哪些不是?为什么?××××××√※思考:你认为数轴最重要的哪三点?正方向数轴的三要素原点画数轴时要注意以下四点:⒈画直线.⒉在直线上取一点作为原点.
⒊确定正方向,并用箭头表示.⒋根据需要选取适当单位长度. 画数轴要体现出数轴的三要素:原点、正方向、长度单位.所有的有理数都可以用数轴的点表示出来.活动31、画数轴3.53、问题:在数轴上能否实际画出表示一千万分之一的点?这个点存在吗?不能这个点存在活动41、观察数轴上的点的特点:数轴上表示数3的点在原点的右边,与原点的距离是3个单位长度;表示数-2的点在原点的左边,与原点的距离是2个单位长度.一般地,设a是一个正数,则数轴上表示数a的点在原点的______边,与原点的距离是______个单位长度;表示数-a的点在原点的______边,与原点的距离是______个单位长度.右a左a活动5例题1(1)画 出数轴并表示下列有理数:(2)写出数轴上点A、B、C、D、E表示的数:点A表示0点B表示-2点C表示1点D表示2.5点E表示-30123解:练习画出数轴,并用数轴上的点表示下列各数:3|2-5,0,5,-4,-3|2,45-5-4-3-2-1-3|23|2(1)若点A表示-3,把A向右移动7个单位长度,则终点表示的数是 。
(2)若点A表示3,把A向左移动7个单位长度,再向右移动的4个单位长度,则终点表示的数是 。
(3)若把点B向右移动3个单位长度,再向左移动4个单位长度,终点表示的数是0,则点B所表示的数是 。.如图,点A与点B的距离是3个单位长度的木条,当木条左端A点落在-9与-8之间,B点落在哪两个整数之间?.如图,以P点为圆心,3个单位长度为半径画圆,该圆与数轴交点表示的数是多少?(1)数轴概念:一般地,在数学中人们用画图把数“直观化”.通常用一条直线上的点表示数,这条直线叫做数轴.(2)数轴的三要素:原点、正方向、长度单位(3)数与形的关系:一 一对应的关系.(4)数学思想:数形结合的思想.3、小结1.下图是五个城市的国际标准时间(单位:时),那么北京时间2012年8月17日上午9时应是( )AA.伦敦时间2012年8月17日凌晨1时
B.纽约时间2012年8月17日晚上22时
C.多伦多时间2012年8月16日晚上20时
D.首尔时间2012年8月17日上午8时在数轴上表示有理数例题2如图所示.解析:画一条数轴,并在数轴上标出表示下列各数的点.2,-4,5,0, ,-0.5,+ . 本题考查数轴的意义及画法,并能将给出的点标在数轴上.根据所给数据,画一条直线,建立适当的数轴来确定它的原点、正方向和单位长度,最后将所给出的点一个不落地标在数轴上.点评:2.下列语句中,正确的是( )
A.任何一个有理数都能在数轴上找到表示它的点
B.数轴上原点及原点右边的数都表示正数
C.数轴是直线,直线就是数轴
D.数轴上的点只能表示正数和负数A4.在数轴上画出表示下列各数的点,并按照从左到右的顺序将这些数重新排列。解:A→-1 B→-2.5 C→3 D→4.5 E→1.5 F→0解:3.如图,指出数轴上的点各表示什么数?数形结合例题3 如图所示,点A,B分别表示-2和2,结合数轴解
答下列问题.解析: (1) 2(1)将点A向右平移4个单位长度后表示的数是 ;
(2)将点B向左平移4个单位长度,再向右移动6个单位后表示的数为 ;
(3)如果一个点先向左移动5个单位长度,再向右移动2个单位长度后表示3,那么这个点表示的原数是什么? (2) 4 解题的标本方法是在数轴上画出平移后的位置,再判断出它所表示的有理数.本题考查了数轴与有理数的关系,解题中利用了数形结合的方法,增强了数与形之间的相互转化.问题(3)需运用逆向思维,培养学生的想象力.点评: (3)如图,由图可得这个点表示的原数是6.5.点A为数轴上表示-2的动点,当A点沿数轴移动4个单位长度到达点B时,点B所表示的有理数为( )
A.2 B.-6 C.2或-6 D.不同于以上答案C(2)6+5+4+2=17(m) (3)由数轴可知,A,D两点间的距离是7m.(1)如图所示: 解:6.小强在建设大路上的通江街车站上的一点O处等人,由于天气较冷,小强来回踱步.他从O点开始,向东行到6m到达一点A处,又由A处向西行走5m,到达一点B处,再由B点继续向西走4m,到达一点C处,最后由C点向东走2m到达一点D处.如果将建设大路看成是一条数轴,通江街车站上一点O处为原点,1m长为一个单位长度,向东的方向为正方向,解答下列问题.
(1)在数轴上标出点O,A,B,C,D;
(2)求小强从O点出发到达D点时所走过的路程;
(3)求数轴上A,D两点间的距离.你能描述一下温度计是怎样表示温度的吗?请带着下列问题阅读教科书: (1)画数轴的步骤是什么?
(2)根据上述实例的经验,“原点”起什么作用?
(3)你是怎么理解“选取适当的长度为单位长度”的?
(4)数轴上,在原点的右边,离原点越远的点所表示
的数 ;在原点的左边,离原点越远的
点所表示的数 -.
作业教材14页复习巩固2,3题
分数正整数 零负整数正分数负分数有理数正有理数零负有理数正整数正分数负整数负分数在小学里,我们曾用以下的方法表示正数和0为什么你会用这样的方法?直观,易懂! 古代部落酋长上任时先在绳上打了个红绳结表示财物往来从0开始,如捕获一只羊在红绳结右边顺次打一个结,每向其他部落借出一只羊就在红绳结左边顺次打一个结,你能解读如图所示A、B绳结的含义吗? 穿越时空 B (左)红绳结(右) A 在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.引入37.5-3-4.8东西汽车站柳树杨树槐树电线杆0活动2学习数轴概念:一般地,在数学中人们用画图把数“直观化”。通常用一条直线上的点表示数,这条直线叫做数轴.教师讲解、学生理解(1)在直线上任取一个点表示数0,这个点叫做原点;(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法表示-1,-2,-3,…例1.判断下面哪些是数轴,哪些不是?为什么?××××××√※思考:你认为数轴最重要的哪三点?正方向数轴的三要素原点画数轴时要注意以下四点:⒈画直线.⒉在直线上取一点作为原点.
⒊确定正方向,并用箭头表示.⒋根据需要选取适当单位长度. 画数轴要体现出数轴的三要素:原点、正方向、长度单位.所有的有理数都可以用数轴的点表示出来.活动31、画数轴3.53、问题:在数轴上能否实际画出表示一千万分之一的点?这个点存在吗?不能这个点存在活动41、观察数轴上的点的特点:数轴上表示数3的点在原点的右边,与原点的距离是3个单位长度;表示数-2的点在原点的左边,与原点的距离是2个单位长度.一般地,设a是一个正数,则数轴上表示数a的点在原点的______边,与原点的距离是______个单位长度;表示数-a的点在原点的______边,与原点的距离是______个单位长度.右a左a活动5例题1(1)画 出数轴并表示下列有理数:(2)写出数轴上点A、B、C、D、E表示的数:点A表示0点B表示-2点C表示1点D表示2.5点E表示-30123解:练习画出数轴,并用数轴上的点表示下列各数:3|2-5,0,5,-4,-3|2,45-5-4-3-2-1-3|23|2(1)若点A表示-3,把A向右移动7个单位长度,则终点表示的数是 。
(2)若点A表示3,把A向左移动7个单位长度,再向右移动的4个单位长度,则终点表示的数是 。
(3)若把点B向右移动3个单位长度,再向左移动4个单位长度,终点表示的数是0,则点B所表示的数是 。.如图,点A与点B的距离是3个单位长度的木条,当木条左端A点落在-9与-8之间,B点落在哪两个整数之间?.如图,以P点为圆心,3个单位长度为半径画圆,该圆与数轴交点表示的数是多少?(1)数轴概念:一般地,在数学中人们用画图把数“直观化”.通常用一条直线上的点表示数,这条直线叫做数轴.(2)数轴的三要素:原点、正方向、长度单位(3)数与形的关系:一 一对应的关系.(4)数学思想:数形结合的思想.3、小结1.下图是五个城市的国际标准时间(单位:时),那么北京时间2012年8月17日上午9时应是( )AA.伦敦时间2012年8月17日凌晨1时
B.纽约时间2012年8月17日晚上22时
C.多伦多时间2012年8月16日晚上20时
D.首尔时间2012年8月17日上午8时在数轴上表示有理数例题2如图所示.解析:画一条数轴,并在数轴上标出表示下列各数的点.2,-4,5,0, ,-0.5,+ . 本题考查数轴的意义及画法,并能将给出的点标在数轴上.根据所给数据,画一条直线,建立适当的数轴来确定它的原点、正方向和单位长度,最后将所给出的点一个不落地标在数轴上.点评:2.下列语句中,正确的是( )
A.任何一个有理数都能在数轴上找到表示它的点
B.数轴上原点及原点右边的数都表示正数
C.数轴是直线,直线就是数轴
D.数轴上的点只能表示正数和负数A4.在数轴上画出表示下列各数的点,并按照从左到右的顺序将这些数重新排列。解:A→-1 B→-2.5 C→3 D→4.5 E→1.5 F→0解:3.如图,指出数轴上的点各表示什么数?数形结合例题3 如图所示,点A,B分别表示-2和2,结合数轴解
答下列问题.解析: (1) 2(1)将点A向右平移4个单位长度后表示的数是 ;
(2)将点B向左平移4个单位长度,再向右移动6个单位后表示的数为 ;
(3)如果一个点先向左移动5个单位长度,再向右移动2个单位长度后表示3,那么这个点表示的原数是什么? (2) 4 解题的标本方法是在数轴上画出平移后的位置,再判断出它所表示的有理数.本题考查了数轴与有理数的关系,解题中利用了数形结合的方法,增强了数与形之间的相互转化.问题(3)需运用逆向思维,培养学生的想象力.点评: (3)如图,由图可得这个点表示的原数是6.5.点A为数轴上表示-2的动点,当A点沿数轴移动4个单位长度到达点B时,点B所表示的有理数为( )
A.2 B.-6 C.2或-6 D.不同于以上答案C(2)6+5+4+2=17(m) (3)由数轴可知,A,D两点间的距离是7m.(1)如图所示: 解:6.小强在建设大路上的通江街车站上的一点O处等人,由于天气较冷,小强来回踱步.他从O点开始,向东行到6m到达一点A处,又由A处向西行走5m,到达一点B处,再由B点继续向西走4m,到达一点C处,最后由C点向东走2m到达一点D处.如果将建设大路看成是一条数轴,通江街车站上一点O处为原点,1m长为一个单位长度,向东的方向为正方向,解答下列问题.
(1)在数轴上标出点O,A,B,C,D;
(2)求小强从O点出发到达D点时所走过的路程;
(3)求数轴上A,D两点间的距离.你能描述一下温度计是怎样表示温度的吗?请带着下列问题阅读教科书: (1)画数轴的步骤是什么?
(2)根据上述实例的经验,“原点”起什么作用?
(3)你是怎么理解“选取适当的长度为单位长度”的?
(4)数轴上,在原点的右边,离原点越远的点所表示
的数 ;在原点的左边,离原点越远的
点所表示的数 -.
作业教材14页复习巩固2,3题
