相反数课件
图片预览





文档简介
课件17张PPT。1.2 有理数(第3课时)
1.2.3 相反数义务教育教科书 数学 七年级 上册课件说明本节课学习相反数的意义和概念.
学习目标:
理解相反数的意义和概念,会求一个数的相反数.
学习重点:
能根据相反数的概念进行符号的化简.
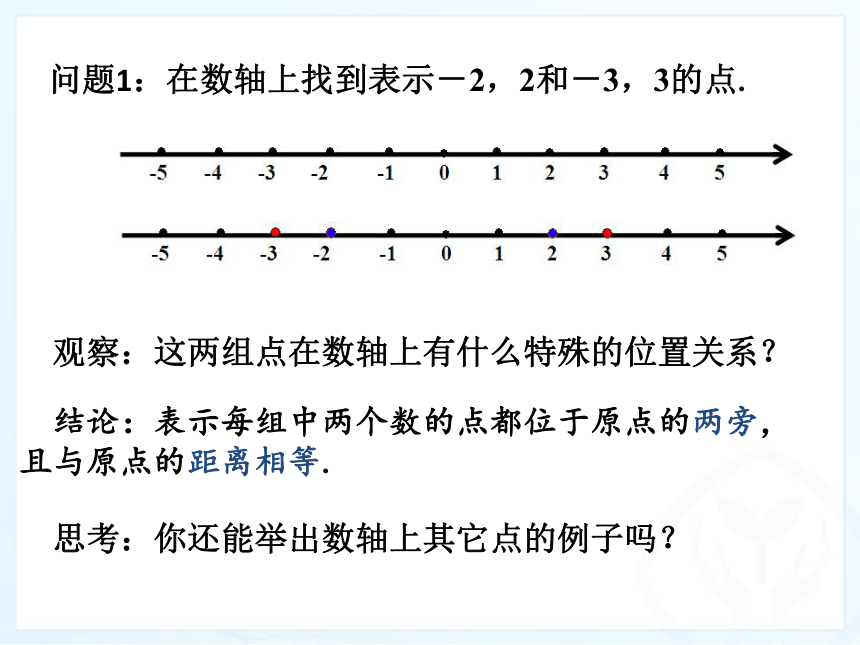
问题1:在数轴上找到表示-2,2和-3,3的点. 结论:表示每组中两个数的点都位于原点的两旁,
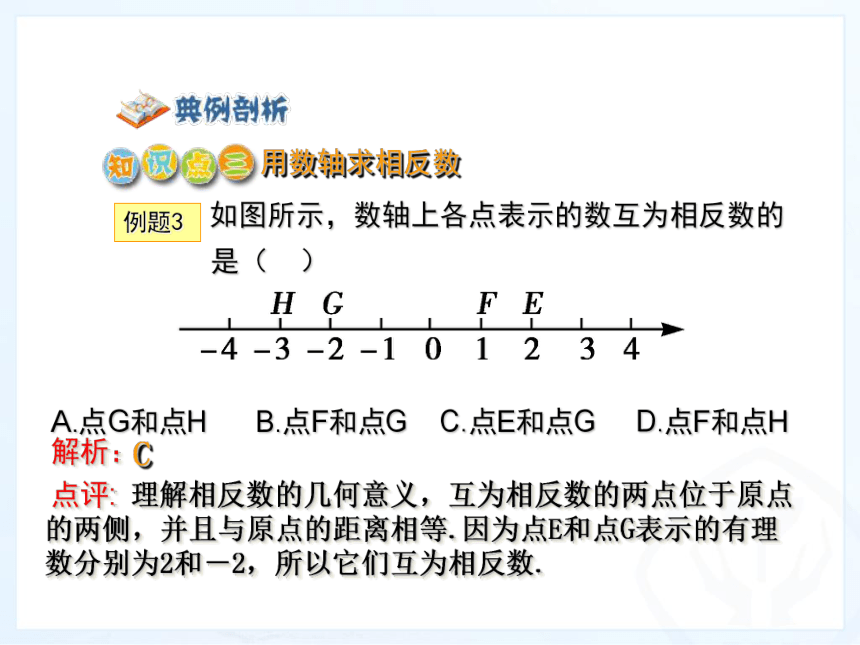
且与原点的距离相等.思考:你还能举出数轴上其它点的例子吗?观察:这两组点在数轴上有什么特殊的位置关系?问题2:观察数轴,说出在数轴上与原点的距离是 2的点有几个?这些点各表示哪些数?设a是一个正数,数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?结论:数轴上与原点的距离是 2的点有两个,表示为-2和2;如果a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示为-a和a,我们说这两个点关于原点对称.相反数: 像2与-2,+5与-5这样只有符号不同的两个数叫做互为相反数,把其中的一个数叫做另一个数的相反数. .特别地,0的相反数是0.问题3:你能再举出几组互为相反数的数的例子吗?小游戏:一个学生说出一个数,然后指定另一名学生回答它的相反数,两人再交换出题,比一比,看哪组回答的又快又准.用数轴求相反数例题3 如图所示,数轴上各点表示的数互为相反数的
是( )
A.点G和点H B.点F和点G C.点E和点G D.点F和点H解析: C 理解相反数的几何意义,互为相反数的两点位于原点的两侧,并且与原点的距离相等.因为点E和点G表示的有理数分别为2和-2,所以它们互为相反数.点评: 在数轴上位于原点的两侧,离原点的距离相等的两个点所表示的数互为相反数. A2.下列各组数中,互为相反数的是( )
A.-(-8)和-8 B.3.2和-4.5
C.0.3和-0.31 D.-(+8)和+(-8)A问题4:你能说出正数、负数和零的相反数分别是什么吗?a的相反数怎么表示?如:5的相反数是-5;-7的相反数是- (-7);
若两个数a、b互为相反数,就可得到a+b=0 ;
反之,若a+b=0,则a、b互为相反数.结论:正数的相反数是负数,负数的相反数是正数,0的相反数是0,a的相反数是-a.教师解释: a可表示任意数——正数、负数、0,求任意一个数的相反数就可以在这个数前加一个“-”号.化简多重符号例题2解析:简化下列各数的符号.(1)-(+5); (2)-(-5); (3)+(+5);
(4)+(-5); (5)-[-(+5)]; (6)+[-(-6)].(1)-(+5)=-5;(2)-(-5)=5;(3)+(+5)=5;(4)+(-5)=-5;(5)-[-(+5)]=5;(6)+[-(-6)]=6. 一个数的前面有偶数个“-”,结果为正,一个数前面有奇数个“-”,结果为负,“+”的个数不影响化简的结果.也可以理解为“同号得正,异号得负” .点评:简化符号:
-(-6)=______; +(-6)=________;
-(+0.73)=_______;-0=________;
-(-34)=________; -(- ) ________.问题5:如何进行符号化简呢?你能自己总结出简化符号的规律吗?师生共同总结:括号外的符号与括号内的符号同号,则化简符号后的数是正数;括号内、外符号异号,则化简符号后的数是负数.练习 教科书第11页
写出下列各数的相反数:
6,-8,-3.9, , ,100 ,0 .课堂小结:说说你对相反数的认识?1.相反数的概念及表示方法;
2.相反数的代数意义与几何意义;
3.多重符号的化简;B3.如果一个数的相反数是最小的正整数,则这个数是 .-11.下列语句,正确的个数是( )
①一个数的相反数等于- ,那么这个数是 ②一个数的相反数是非正数,那么这个数一定是正数③符号不同的两个数互为相反数④一个数的相反数的相反数是它本身
A.1个 B.2个 C.3个 D.4个-0.53.5C6.在数轴上与原点距离是4的点表示的数是( )
A.4 B.-4 C.±4 D.88.在数轴上标记出-3,2,0,-3.5各数与它们的相反数,并说明它们与其相反数在数轴上表示的点到原点的距离有什么关系? C A与C解:下节课我们继续学习!再见
学习目标:
理解相反数的意义和概念,会求一个数的相反数.
学习重点:
能根据相反数的概念进行符号的化简.
问题1:在数轴上找到表示-2,2和-3,3的点. 结论:表示每组中两个数的点都位于原点的两旁,
且与原点的距离相等.思考:你还能举出数轴上其它点的例子吗?观察:这两组点在数轴上有什么特殊的位置关系?问题2:观察数轴,说出在数轴上与原点的距离是 2的点有几个?这些点各表示哪些数?设a是一个正数,数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?结论:数轴上与原点的距离是 2的点有两个,表示为-2和2;如果a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示为-a和a,我们说这两个点关于原点对称.相反数: 像2与-2,+5与-5这样只有符号不同的两个数叫做互为相反数,把其中的一个数叫做另一个数的相反数. .特别地,0的相反数是0.问题3:你能再举出几组互为相反数的数的例子吗?小游戏:一个学生说出一个数,然后指定另一名学生回答它的相反数,两人再交换出题,比一比,看哪组回答的又快又准.用数轴求相反数例题3 如图所示,数轴上各点表示的数互为相反数的
是( )
A.点G和点H B.点F和点G C.点E和点G D.点F和点H解析: C 理解相反数的几何意义,互为相反数的两点位于原点的两侧,并且与原点的距离相等.因为点E和点G表示的有理数分别为2和-2,所以它们互为相反数.点评: 在数轴上位于原点的两侧,离原点的距离相等的两个点所表示的数互为相反数. A2.下列各组数中,互为相反数的是( )
A.-(-8)和-8 B.3.2和-4.5
C.0.3和-0.31 D.-(+8)和+(-8)A问题4:你能说出正数、负数和零的相反数分别是什么吗?a的相反数怎么表示?如:5的相反数是-5;-7的相反数是- (-7);
若两个数a、b互为相反数,就可得到a+b=0 ;
反之,若a+b=0,则a、b互为相反数.结论:正数的相反数是负数,负数的相反数是正数,0的相反数是0,a的相反数是-a.教师解释: a可表示任意数——正数、负数、0,求任意一个数的相反数就可以在这个数前加一个“-”号.化简多重符号例题2解析:简化下列各数的符号.(1)-(+5); (2)-(-5); (3)+(+5);
(4)+(-5); (5)-[-(+5)]; (6)+[-(-6)].(1)-(+5)=-5;(2)-(-5)=5;(3)+(+5)=5;(4)+(-5)=-5;(5)-[-(+5)]=5;(6)+[-(-6)]=6. 一个数的前面有偶数个“-”,结果为正,一个数前面有奇数个“-”,结果为负,“+”的个数不影响化简的结果.也可以理解为“同号得正,异号得负” .点评:简化符号:
-(-6)=______; +(-6)=________;
-(+0.73)=_______;-0=________;
-(-34)=________; -(- ) ________.问题5:如何进行符号化简呢?你能自己总结出简化符号的规律吗?师生共同总结:括号外的符号与括号内的符号同号,则化简符号后的数是正数;括号内、外符号异号,则化简符号后的数是负数.练习 教科书第11页
写出下列各数的相反数:
6,-8,-3.9, , ,100 ,0 .课堂小结:说说你对相反数的认识?1.相反数的概念及表示方法;
2.相反数的代数意义与几何意义;
3.多重符号的化简;B3.如果一个数的相反数是最小的正整数,则这个数是 .-11.下列语句,正确的个数是( )
①一个数的相反数等于- ,那么这个数是 ②一个数的相反数是非正数,那么这个数一定是正数③符号不同的两个数互为相反数④一个数的相反数的相反数是它本身
A.1个 B.2个 C.3个 D.4个-0.53.5C6.在数轴上与原点距离是4的点表示的数是( )
A.4 B.-4 C.±4 D.88.在数轴上标记出-3,2,0,-3.5各数与它们的相反数,并说明它们与其相反数在数轴上表示的点到原点的距离有什么关系? C A与C解:下节课我们继续学习!再见
