不等式的简单变形[下学期]

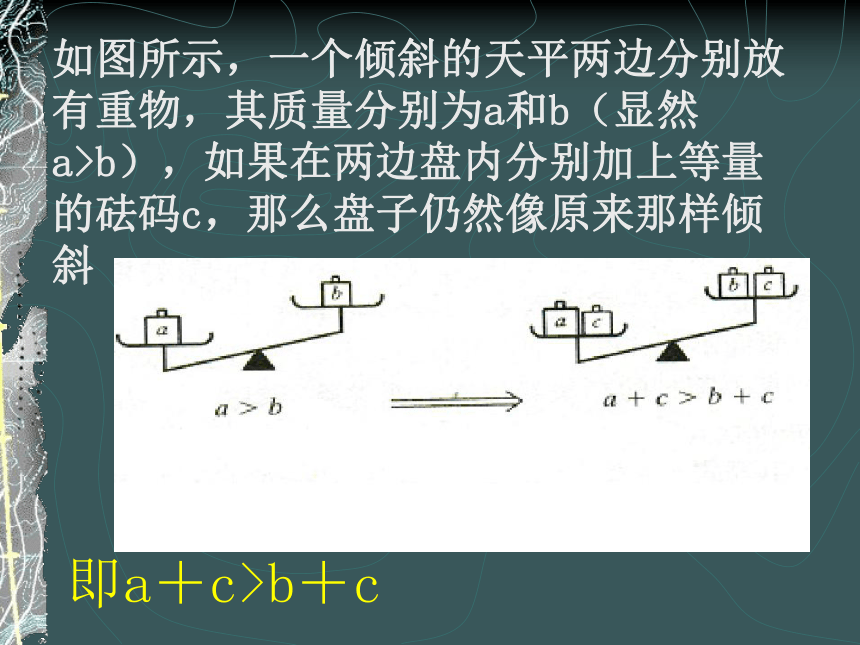
课件14张PPT。不等式的简单变形让我们先做个实验吧！如图所示，一个倾斜的天平两边分别放有重物，其质量分别为a和b（显然a>b），如果在两边盘内分别加上等量的砝码c，那么盘子仍然像原来那样倾斜 即a＋c>b＋c 结论：不等式的性质1：如果a>b，那么a＋c>b＋c，a－c>b－c 这就是说，不等式的两边都加上（或减去）同一个数或同一个整式，不等式的方向不变。 (1)不等式两边都加上(或减去)同一个数或同一个整式，不等号方向如何变化?
思考：不等式的两边都乘以（或除以）同一个不为零的数，不等号的方向是否也不变呢？ 试一试：将不等式7>4两边都乘以同一个数，比较所得的数的大小，用“<”或“>”填空：
7×3_______4×3， 7×2_______4×2，
7×1_______4×1， 7×0_______4×0，
7×（－1）_______4×（－1），
7×（－2）_______4×（－2），
7×（－3）_______4×（－3），从中你能发现什么？ >>>=<<<概括：不等式的性质2 如果a>b，并且c>0，那么ac>bc。
不等式的性质3 如果a>b，并且c<0，那么ac不等式两边都乘以或除以同一负数，不等号方向改变问题探究二例2.设a＞b，用“＜”或“＞”填空：
(1)a-3 b-3 (2) (3) -4a -4b不等式和它的基本性质>><不等式和它的基本性质
1.用“＞”或“＜”在横线上填空，并在题后
括号内填写理由.
∵a＞b (2)∵ a＞b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m＞5n (4)∵4x＞5x
∴ -m ( ) ∴ x 0( )
(5)∵ ＜ (6)∵a-1＜8
∴ a 2b( ) ∴ a 9( ) ＞＞＞＜＜＜不等式基
本性质1不等式基
本性质3不等式基
本性质3不等式基
本性质1不等式基
本性质2不等式基
本性质1不等式和它的基本性质判断正误：
(1)∵a+8＞4 (2)∵3＞2
∴a＞-4 ( ) ∴3a＞2a( )
(3)∵-1＞-2 (4)∵ab＞0
∴a-1＞a-2 ( ) ∴a＞0,b＞ 0( )√×√×与解方程一样，解不等式的过程，就是要将不等式变形成x>a或x（1）x－7<8 解 ：不等式的两边都加上7，不等式的方向不变，所以x－7＋7<8＋7， 得 x<15 （2）3x<2x-3例2：（2）－2x<6
解不等式：
（1） x>－3；