17.1.3 勾股定理同步练习题(含解析)
文档属性
| 名称 | 17.1.3 勾股定理同步练习题(含解析) | 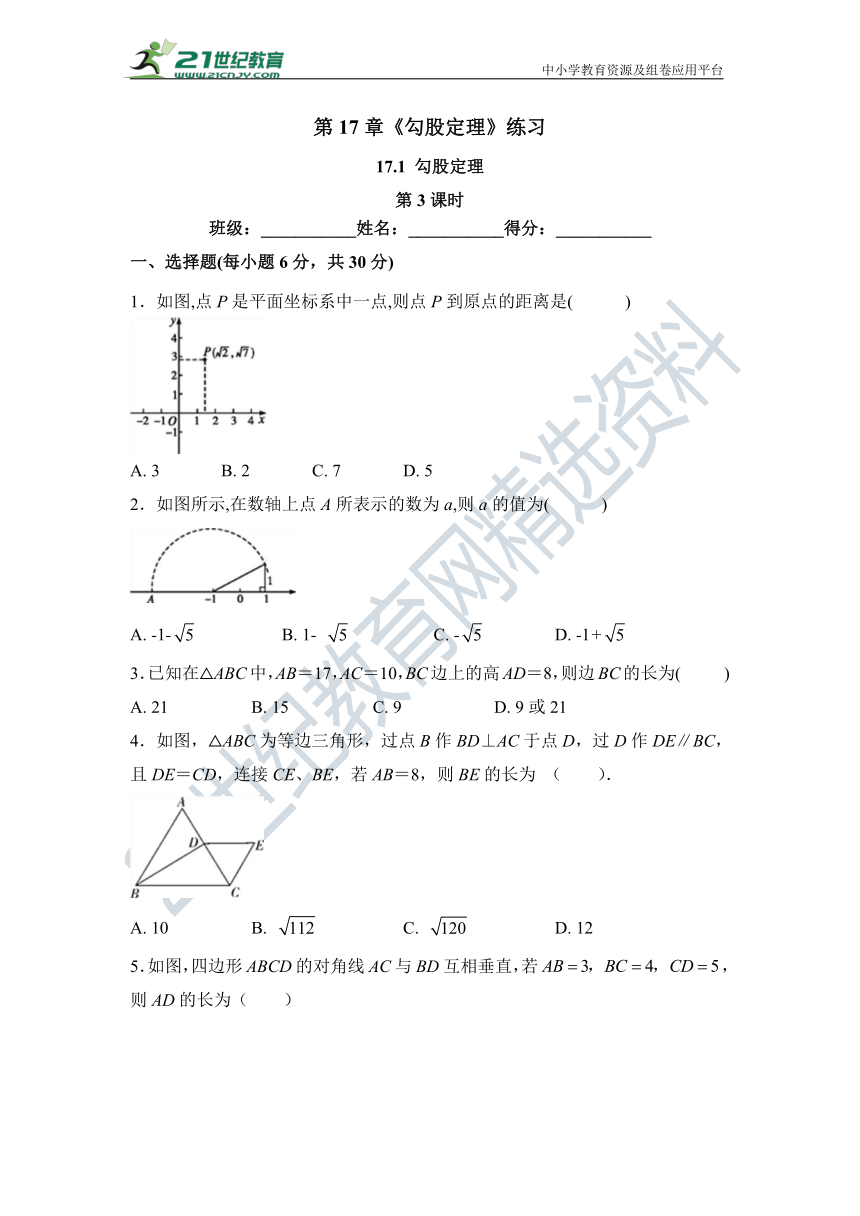 | |
| 格式 | doc | ||
| 文件大小 | 451.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-09 21:45:18 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第17章《勾股定理》练习
17.1 勾股定理
第3课时
班级:___________姓名:___________得分:___________
一、选择题(每小题6分,共30分)
1.如图,点P是平面坐标系中一点,则点P到原点的距离是( )
A. 3 B. 2 C. 7 D. 5
2.如图所示,在数轴上点A所表示的数为a,则a的值为( )
A. -1- B. 1- C. - D. -1+
3.已知在△ABC中,AB=17,AC=10,BC边上的高AD=8,则边BC的长为( )
A. 21 B. 15 C. 9 D. 9或21
4.如图,△ABC为等边三角形,过点B作BD⊥AC于点D,过D作DE∥BC,且DE=CD,连接CE、BE,若AB=8,则BE的长为 ( ).
A. 10 B. C. D. 12
5.如图,四边形ABCD的对角线AC与BD互相垂直,若,则AD的长为( )
A. B. 4 C. D.
二、填空题(每小题6分,共30分)
6.如图,长方形ABCD中,AB=2,AD=1,A,B在数轴上,以B为圆心,BD长为半径作弧交数轴负半轴于点E,则点E表示的实数为___________
7.在所给的8×6网格图中,横竖每相邻两点间的长度均为1,以这些点为顶点的三角形称为网格三角形,请找出点M,使以A,B,M为顶点的网格三角形是直角三角形,这样的点M有_______个.
8.如图,点在以为圆心,以为半径的半圆上,正方形的边长是一个单位长度,则图中点所表示的数是__________,记数对应的点是,则线段的长是__________.
9.定义:如图,点M,N把线段AB分割成三条线段AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点. 若AM=1,MN=2,则BN的长为 .
10.如图,OP=1,过P作且,根据勾股定理,得;再过作且=1,得;又过作且,得OP3=2;…依此继续,得____, _________(n为自然数,且n>0).
三、解答题(共40分)
11.在如图所示的3 ×3 的正方形网格中画出一个△ABC,使AB=,BC=,AC=3,并求出△ABC 的面积.
12.如图,在△ABC中,AB=7,AC=,∠A=45°,AH⊥HC,垂足为H。
(1)求证:△AHC是等腰直角三角形;
(2)求BC的长.
参考答案
1.A
【解析】解:OP=.故选A.
2.A
【解析】解:如图,点A在以O为圆心,OB长为半径的圆上.在直角△BOC中,∵OC=2,BC=1,根据勾股定理知:OB2= OC2+BC2 = 22+12 = 5 ,∴OA=OB=,∴a=.故选A.
3.D
【解析】①∠C为锐角时:
∵Rt△ADC中,,AC=10,AD=8,∴CD2=AC2-AD2=36,∴CD=6;
∵Rt△ADB中,,AB=17,AD=8,∴BD2=AB2-AD2=225,∴BD=15;
∴BC=6+15=21.
②∠ACB为钝角时:
∵Rt△ADC中,,AC=10,AD=8,∴CD2=AC2-AD2=36,∴CD=6;
∵Rt△ADB中,,AB=17,AD=8,∴BD2=AB2-AD2=225,∴BD=15;
∴BC=15-6=9.
综上:BC=9或21.
故选D.
4.B
【解析】∵△ABC为等边三角形,
∴∠ACB=60°,
∵DE∥BC,
∴∠EDC=∠ACB=60°,
又∵DE=DC,
∴△CDE为等边三角形;
过点E作EH⊥BC于H,
,
∵BD⊥AC,
∴CD=AC=AB=4,
又∵△CDE为等边三角形,
∴CE=CD=4,
∵∠ECH=60°,
∴EH=EC sin60°=4×=,CH=EC cos60°=2,BH=10,
∴BE===.
故选:B.
5.A
【解析】解:在Rt△AOB中,AO2=AB2﹣BO2;Rt△DOC中:DO2=DC2﹣CO2;
∴AD2=AO2+DO2=AB2﹣BO2+DC2﹣CO2= AB2 +DC2﹣(BO2+CO2)=18,∴AD==.故选A.
6.1-
【解析】由题意可知,在长方形ABCD中,∠DAB=90°,AB=2,AD=1,
∴BD=,
∴BE=BD=,
又∵点B表示的数是1,点E在点B的左边,
∴点E表示的数为: .
故答案为: .
7.12
【解析】如图,在线段CD和线段EF上各有5个符合条件的点,图中的两个M点也符合要求,所以符合条件的点M共有12个.
8.
【解析】连接OD,由勾股定理可得,
∴,
∴为, ,
故答案为: , .
9.或
【解析】分两种情况:
①当MN为最大线段时,
∵点 M、N是线段AB的勾股分割点,
②当BN为最大线段时,
∵点M、N是线段AB的勾股分割点,
综上所述:BN的长为或
故答案为: 或
10.
【解析】首先根据勾股定理求出OP4,再由OP1,OP2,OP3, OP4,的长度找到规律进而求出OP2018, 的长.
解:由题可知:OP1=,
OP2=,
OP3=,
OP4=,
……
所以 ,
=.
故答案为: , .
11.
【解析】根据勾股定理和正方形网格的特征,画出△ABC即可,利用三角形的面积公式计算即可.
解:如图所示:△ABC中,AB=,BC=,AC=3,
.
12.(1)见解析;(2)BC=5
【解析】(1)先证得∠AHC=90°,再由∠A=45°,即可证得△AHC是等腰直角三角形;(2)设AH=x,则CH=x,BH=7-x,在等腰直角三角形△AHC中,根据勾股定理求得CH=4,即可得BH=3,在Rt△BHC中,根据勾股定理求得BC=5.
(1)证明:∵AH⊥HC,
∴∠AHC=∠BHC=90°,
∵∠A=45°,
∴∠ACH=45°,
∴△AHC是等腰直角三角形;
(2)设AH=x,则CH=x,BH=7-x,
在等腰直角三角形△AHC中,
,
解得x=4.
∴CH=3,BH=4,
在Rt△BHC中,
,
∴BC=5.
第17章《勾股定理》练习
17.1 勾股定理
第3课时
班级:___________姓名:___________得分:___________
一、选择题(每小题6分,共30分)
1.如图,点P是平面坐标系中一点,则点P到原点的距离是( )
A. 3 B. 2 C. 7 D. 5
2.如图所示,在数轴上点A所表示的数为a,则a的值为( )
A. -1- B. 1- C. - D. -1+
3.已知在△ABC中,AB=17,AC=10,BC边上的高AD=8,则边BC的长为( )
A. 21 B. 15 C. 9 D. 9或21
4.如图,△ABC为等边三角形,过点B作BD⊥AC于点D,过D作DE∥BC,且DE=CD,连接CE、BE,若AB=8,则BE的长为 ( ).
A. 10 B. C. D. 12
5.如图,四边形ABCD的对角线AC与BD互相垂直,若,则AD的长为( )
A. B. 4 C. D.
二、填空题(每小题6分,共30分)
6.如图,长方形ABCD中,AB=2,AD=1,A,B在数轴上,以B为圆心,BD长为半径作弧交数轴负半轴于点E,则点E表示的实数为___________
7.在所给的8×6网格图中,横竖每相邻两点间的长度均为1,以这些点为顶点的三角形称为网格三角形,请找出点M,使以A,B,M为顶点的网格三角形是直角三角形,这样的点M有_______个.
8.如图,点在以为圆心,以为半径的半圆上,正方形的边长是一个单位长度,则图中点所表示的数是__________,记数对应的点是,则线段的长是__________.
9.定义:如图,点M,N把线段AB分割成三条线段AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点. 若AM=1,MN=2,则BN的长为 .
10.如图,OP=1,过P作且,根据勾股定理,得;再过作且=1,得;又过作且,得OP3=2;…依此继续,得____, _________(n为自然数,且n>0).
三、解答题(共40分)
11.在如图所示的3 ×3 的正方形网格中画出一个△ABC,使AB=,BC=,AC=3,并求出△ABC 的面积.
12.如图,在△ABC中,AB=7,AC=,∠A=45°,AH⊥HC,垂足为H。
(1)求证:△AHC是等腰直角三角形;
(2)求BC的长.
参考答案
1.A
【解析】解:OP=.故选A.
2.A
【解析】解:如图,点A在以O为圆心,OB长为半径的圆上.在直角△BOC中,∵OC=2,BC=1,根据勾股定理知:OB2= OC2+BC2 = 22+12 = 5 ,∴OA=OB=,∴a=.故选A.
3.D
【解析】①∠C为锐角时:
∵Rt△ADC中,,AC=10,AD=8,∴CD2=AC2-AD2=36,∴CD=6;
∵Rt△ADB中,,AB=17,AD=8,∴BD2=AB2-AD2=225,∴BD=15;
∴BC=6+15=21.
②∠ACB为钝角时:
∵Rt△ADC中,,AC=10,AD=8,∴CD2=AC2-AD2=36,∴CD=6;
∵Rt△ADB中,,AB=17,AD=8,∴BD2=AB2-AD2=225,∴BD=15;
∴BC=15-6=9.
综上:BC=9或21.
故选D.
4.B
【解析】∵△ABC为等边三角形,
∴∠ACB=60°,
∵DE∥BC,
∴∠EDC=∠ACB=60°,
又∵DE=DC,
∴△CDE为等边三角形;
过点E作EH⊥BC于H,
,
∵BD⊥AC,
∴CD=AC=AB=4,
又∵△CDE为等边三角形,
∴CE=CD=4,
∵∠ECH=60°,
∴EH=EC sin60°=4×=,CH=EC cos60°=2,BH=10,
∴BE===.
故选:B.
5.A
【解析】解:在Rt△AOB中,AO2=AB2﹣BO2;Rt△DOC中:DO2=DC2﹣CO2;
∴AD2=AO2+DO2=AB2﹣BO2+DC2﹣CO2= AB2 +DC2﹣(BO2+CO2)=18,∴AD==.故选A.
6.1-
【解析】由题意可知,在长方形ABCD中,∠DAB=90°,AB=2,AD=1,
∴BD=,
∴BE=BD=,
又∵点B表示的数是1,点E在点B的左边,
∴点E表示的数为: .
故答案为: .
7.12
【解析】如图,在线段CD和线段EF上各有5个符合条件的点,图中的两个M点也符合要求,所以符合条件的点M共有12个.
8.
【解析】连接OD,由勾股定理可得,
∴,
∴为, ,
故答案为: , .
9.或
【解析】分两种情况:
①当MN为最大线段时,
∵点 M、N是线段AB的勾股分割点,
②当BN为最大线段时,
∵点M、N是线段AB的勾股分割点,
综上所述:BN的长为或
故答案为: 或
10.
【解析】首先根据勾股定理求出OP4,再由OP1,OP2,OP3, OP4,的长度找到规律进而求出OP2018, 的长.
解:由题可知:OP1=,
OP2=,
OP3=,
OP4=,
……
所以 ,
=.
故答案为: , .
11.
【解析】根据勾股定理和正方形网格的特征,画出△ABC即可,利用三角形的面积公式计算即可.
解:如图所示:△ABC中,AB=,BC=,AC=3,
.
12.(1)见解析;(2)BC=5
【解析】(1)先证得∠AHC=90°,再由∠A=45°,即可证得△AHC是等腰直角三角形;(2)设AH=x,则CH=x,BH=7-x,在等腰直角三角形△AHC中,根据勾股定理求得CH=4,即可得BH=3,在Rt△BHC中,根据勾股定理求得BC=5.
(1)证明:∵AH⊥HC,
∴∠AHC=∠BHC=90°,
∵∠A=45°,
∴∠ACH=45°,
∴△AHC是等腰直角三角形;
(2)设AH=x,则CH=x,BH=7-x,
在等腰直角三角形△AHC中,
,
解得x=4.
∴CH=3,BH=4,
在Rt△BHC中,
,
∴BC=5.
