用相同的正多边形拼地板[下学期]
图片预览





文档简介
课件21张PPT。9.3 .1 用相同的正多边形拼地板① n边形的内角和公式:② 正多边形每个内角=(n-2) ×180° 什么是正多边形?如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形。外角和360°生活中还看到过哪些多边形可用来铺地板呢?
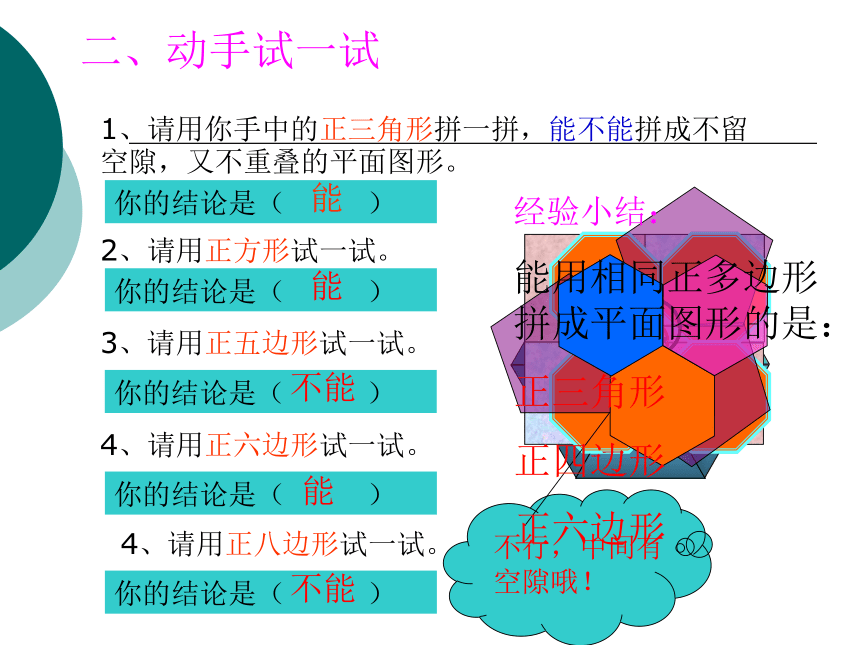
一、观察生活中的图片二、动手试一试1、请用你手中的正三角形拼一拼,能不能拼成不留空隙,又不重叠的平面图形。2、请用正方形试一试。你的结论是( ) 能你的结论是( ) 能3、请用正五边形试一试。你的结论是( ) 不能4、请用正六边形试一试。你的结论是( ) 能4、请用正八边形试一试。你的结论是( ) 不能不行,中间有空隙哦!经验小结:
能用相同正多边形拼成平面图形的是:
正三角形
正四边形
正六边形思考: 为什么有的正多边形可以拼满地板,但有的又不可以呢?
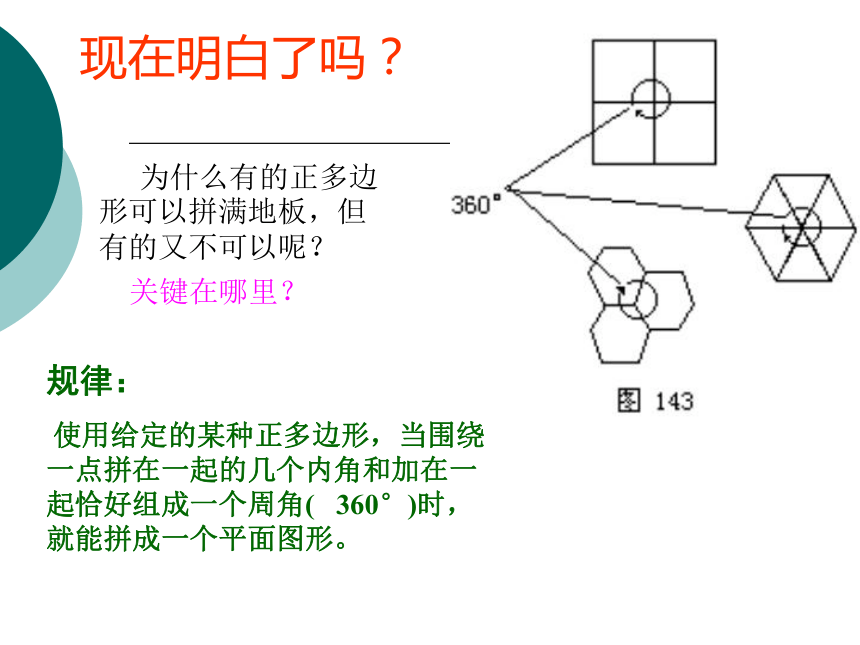
关键在哪里?180度360度540度720度900度(n-2)×18060度90度108度120度约129度请填下表,看是否与每个内角的度数有关。层层深入现在明白了吗? 为什么有的正多边形可以拼满地板,但有的又不可以呢?
关键在哪里?
规律:
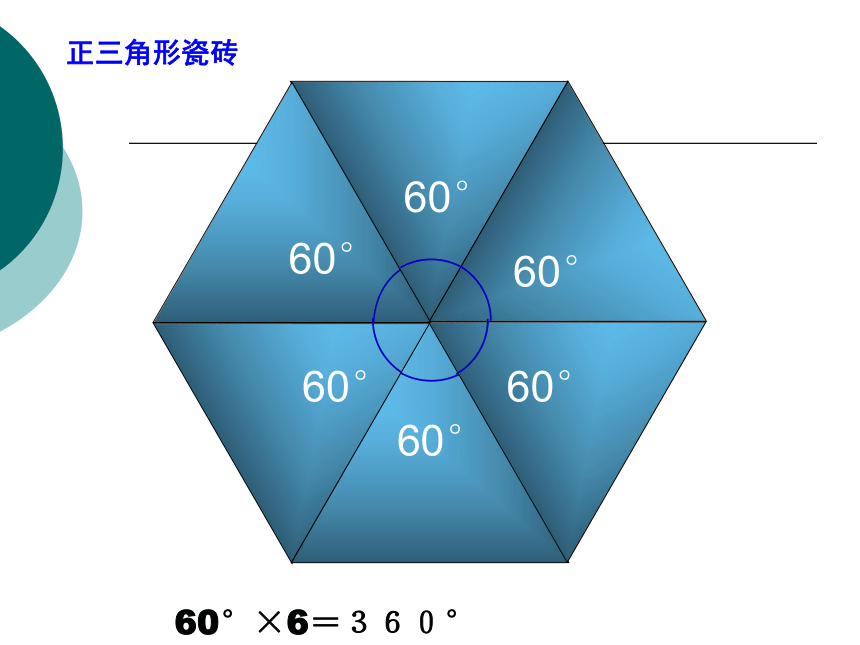
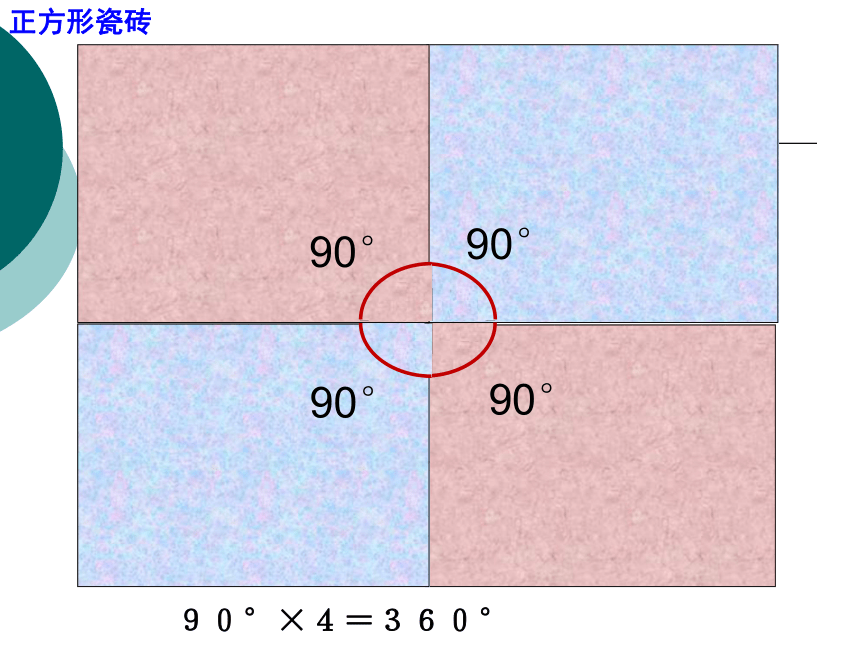
使用给定的某种正多边形,当围绕一点拼在一起的几个内角和加在一起恰好组成一个周角( 360°)时,就能拼成一个平面图形。60°60°60°60°60°60°正三角形瓷砖60°×6=360°90°90°90°90°正方形瓷砖90°×4=360°108°108°108°正五边形瓷砖108°×3=324°正六边形瓷砖120°×3=360°正八边形瓷砖135。135。135。135°×3=405°正八边形瓷砖135°×3=405°小结:
如果,正多边形一个内角度数×正多边形个数= 时,可铺地板。120°×3=360°不能正六边形瓷砖能360o这就说明:当 360°÷
即
为正整数时,用这样的n边形就可以铺满地板.探究 = =2+
n只能是哪些数? 3 4 6化简后剪出一些相同的任意形状的四边形,拼拼看,能否铺满地面。做一做1234 不规则四边形能用来铺地板的道理是:“任意四边形(指凸四边形)内角之和都等于360°。”因此,不管切下的四边形怎样歪七扭八,只要形状完全相同,4块相拼就能凑成360°,而且总能找到等长的边相接,使砖与砖之间不留缝隙。关键:每个四边形都用不同的角围绕一点拼在一起。思考:用相同的任意形状的三角形呢?例1.正十边形能不能铺满平面?为什么?分析:一个正多边形能不能铺满平面,只要看周角360°能否被一个内角度数整除,若能整除,则能铺满平面;若不能整除,则不能铺满平面解:因为正十边形每内角为144°
又因为周角360°不能被144°整除,所以正十边形不能铺满平面
例题讲述练习题: 选择题: CCA填空题: 1.围绕一点,拼在一起的几个内角相加为_______时,此正n边形可铺满整个地面,
没有空隙。 360°判断题:
1.任意一种正多边形都能铺满地面.( )
2.任意一种等腰三角形都能铺满地面.( )
3.任意一种梯形都能铺满地面.( )
4.只要多边形的各边相等,就一定能铺满地面.( )×√√×练习:课本P72第1题
课本P72第2题
今天你学到了什么??1.通过实验与探究,掌握了能用同一种正多边形拼地板 的正多边形有正三角形、正方形、正六边形。3.在探究的过程中,理解了正多边形能够拼地板的道理。 2.正多边形个数×正多边形内角度数=360o 为正整数时,用这样的n边形就可以铺满地板.
一、观察生活中的图片二、动手试一试1、请用你手中的正三角形拼一拼,能不能拼成不留空隙,又不重叠的平面图形。2、请用正方形试一试。你的结论是( ) 能你的结论是( ) 能3、请用正五边形试一试。你的结论是( ) 不能4、请用正六边形试一试。你的结论是( ) 能4、请用正八边形试一试。你的结论是( ) 不能不行,中间有空隙哦!经验小结:
能用相同正多边形拼成平面图形的是:
正三角形
正四边形
正六边形思考: 为什么有的正多边形可以拼满地板,但有的又不可以呢?
关键在哪里?180度360度540度720度900度(n-2)×18060度90度108度120度约129度请填下表,看是否与每个内角的度数有关。层层深入现在明白了吗? 为什么有的正多边形可以拼满地板,但有的又不可以呢?
关键在哪里?
规律:
使用给定的某种正多边形,当围绕一点拼在一起的几个内角和加在一起恰好组成一个周角( 360°)时,就能拼成一个平面图形。60°60°60°60°60°60°正三角形瓷砖60°×6=360°90°90°90°90°正方形瓷砖90°×4=360°108°108°108°正五边形瓷砖108°×3=324°正六边形瓷砖120°×3=360°正八边形瓷砖135。135。135。135°×3=405°正八边形瓷砖135°×3=405°小结:
如果,正多边形一个内角度数×正多边形个数= 时,可铺地板。120°×3=360°不能正六边形瓷砖能360o这就说明:当 360°÷
即
为正整数时,用这样的n边形就可以铺满地板.探究 = =2+
n只能是哪些数? 3 4 6化简后剪出一些相同的任意形状的四边形,拼拼看,能否铺满地面。做一做1234 不规则四边形能用来铺地板的道理是:“任意四边形(指凸四边形)内角之和都等于360°。”因此,不管切下的四边形怎样歪七扭八,只要形状完全相同,4块相拼就能凑成360°,而且总能找到等长的边相接,使砖与砖之间不留缝隙。关键:每个四边形都用不同的角围绕一点拼在一起。思考:用相同的任意形状的三角形呢?例1.正十边形能不能铺满平面?为什么?分析:一个正多边形能不能铺满平面,只要看周角360°能否被一个内角度数整除,若能整除,则能铺满平面;若不能整除,则不能铺满平面解:因为正十边形每内角为144°
又因为周角360°不能被144°整除,所以正十边形不能铺满平面
例题讲述练习题: 选择题: CCA填空题: 1.围绕一点,拼在一起的几个内角相加为_______时,此正n边形可铺满整个地面,
没有空隙。 360°判断题:
1.任意一种正多边形都能铺满地面.( )
2.任意一种等腰三角形都能铺满地面.( )
3.任意一种梯形都能铺满地面.( )
4.只要多边形的各边相等,就一定能铺满地面.( )×√√×练习:课本P72第1题
课本P72第2题
今天你学到了什么??1.通过实验与探究,掌握了能用同一种正多边形拼地板 的正多边形有正三角形、正方形、正六边形。3.在探究的过程中,理解了正多边形能够拼地板的道理。 2.正多边形个数×正多边形内角度数=360o 为正整数时,用这样的n边形就可以铺满地板.
