人教版八年级下册 18.1.1 平行四边形的性质 课件(共22张PPT)
文档属性
| 名称 | 人教版八年级下册 18.1.1 平行四边形的性质 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 952.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 09:20:35 | ||
图片预览


文档简介
(共22张PPT)
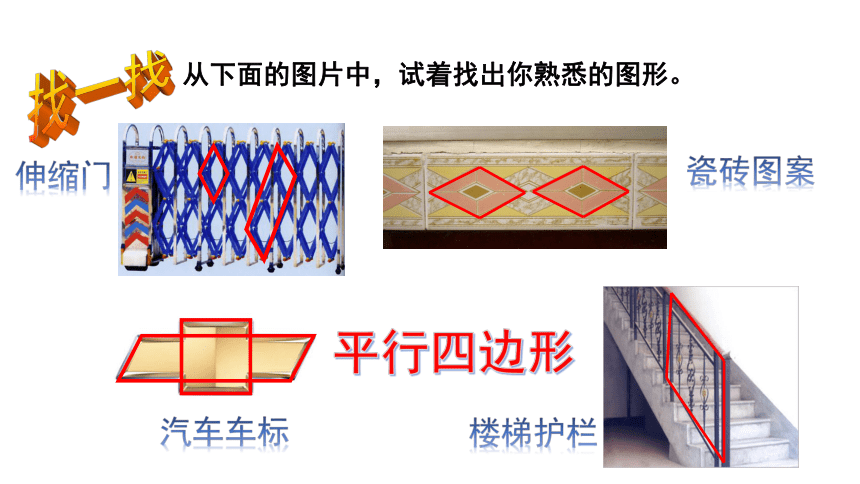
思考:回忆以前,我们是按照怎样的思路来研究三角形的呢?
一般三角形
等腰三角形
等边三角形
直角三角形
特殊三角形
定义
性质
判定
四边形
平行四边形
应用
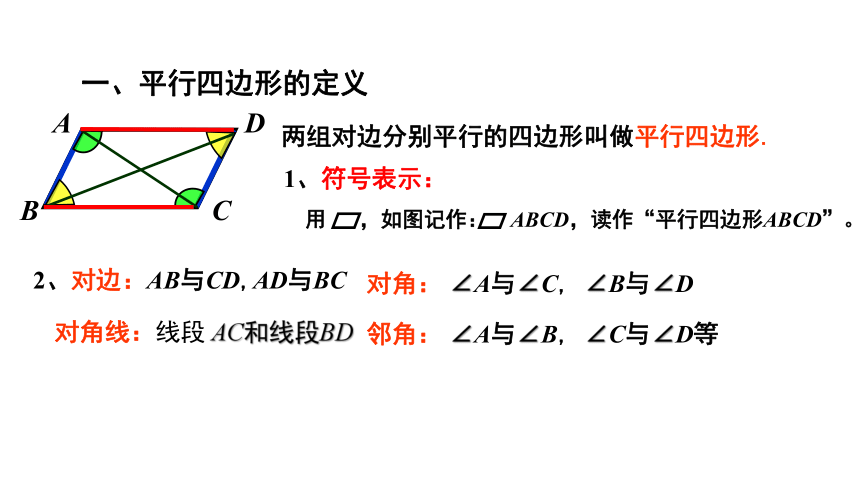
伸缩门
找一找
从下面的图片中,试着找出你熟悉的图形。
瓷砖图案
楼梯护栏
平行四边形
汽车车标
18.1.1 平行四边形(1)
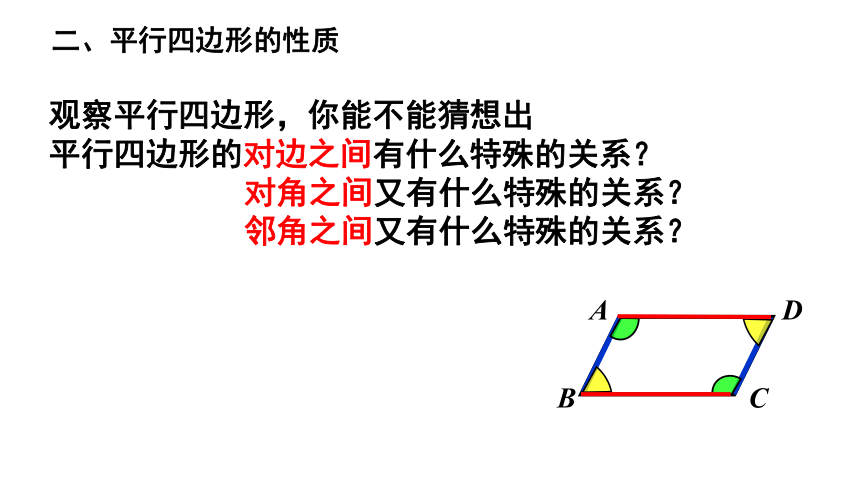
两组对边分别平行的四边形叫做平行四边形.
一、平行四边形的定义
A
B
C
D
1、符号表示:
用 ,如图记作: ABCD,读作“平行四边形ABCD”。
2、对边:AB与CD,AD与BC
对角: ∠A与∠C, ∠B与∠D
邻角: ∠A与∠B, ∠C与∠D等
对角线:线段 AC和线段BD
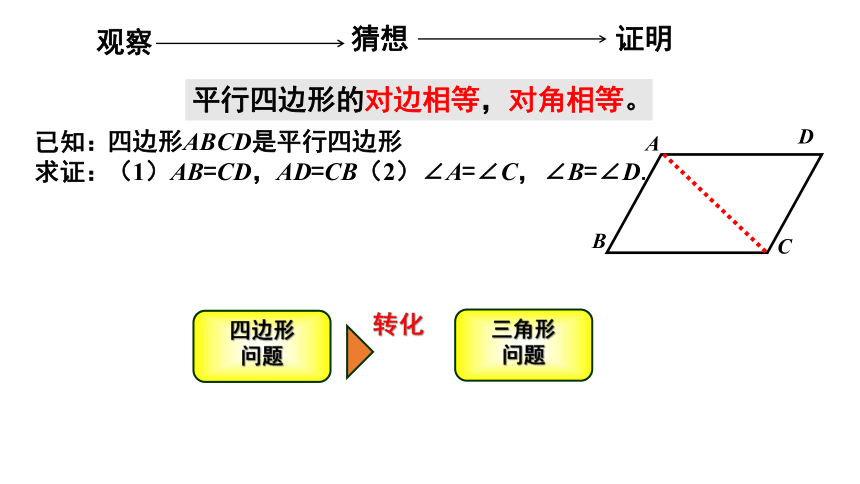
观察平行四边形,你能不能猜想出
平行四边形的对边之间有什么特殊的关系?
对角之间又有什么特殊的关系?
邻角之间又有什么特殊的关系?
二、平行四边形的性质
A
B
C
D
A
B
C
D
四边形ABCD是平行四边形
(1)AB=CD,AD=CB(2)∠A=∠C,∠B=∠D.
已知:
求证:
平行四边形的对边相等,对角相等。
四边形
问题
三角形
问题
转化
证明
猜想
观察
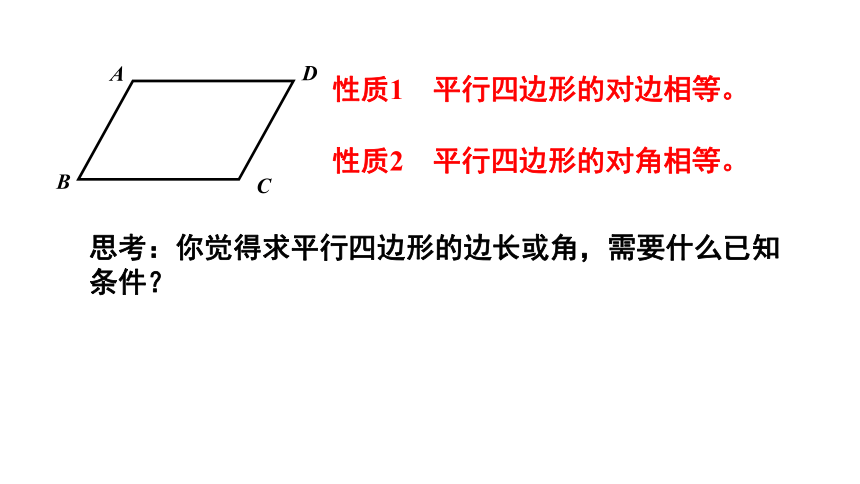
性质1 平行四边形的对边相等。
性质2 平行四边形的对角相等。
A
B
C
D
思考:你觉得求平行四边形的边长或角,需要什么已知条件?
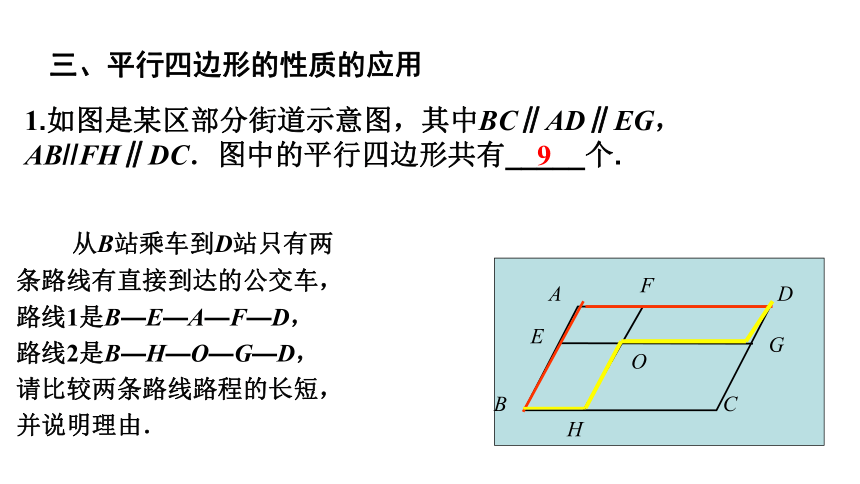
1.如图是某区部分街道示意图,其中BC∥AD∥EG,AB//FH∥DC.图中的平行四边形共有_____个.
9
A
B
C
D
E
G
F
H
O
从B站乘车到D站只有两
条路线有直接到达的公交车,
路线1是B—E—A—F—D,
路线2是B—H—O—G—D,
请比较两条路线路程的长短,
并说明理由.
三、平行四边形的性质的应用
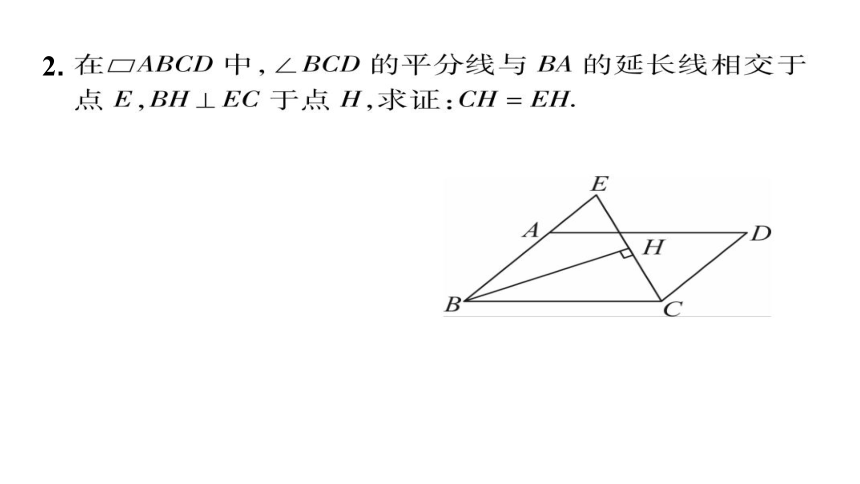
2.
3.如图, ABCD 中,DE⊥AB,BF⊥CD,
垂足分别为E,F.求证:AE=CF.
A
B
C
D
E
F
A
B
C
D
E
F
a
b
AD与BC
对边
相等
N1
M1
Q1
P1
N2
M2
Q2
P2
N3
M3
Q3
P3
M1N1//P1Q1
M2N2//P2Q2
M3N3//P3Q3
AD//BC
相等
相等
相等
结论:夹在两条平行线间的平行线段相等。
a
b
N3
M3
Q3
P3
结论:夹在两条平行线间的平行线段相等。
A
B
C
D
AD与BC
对边
相等
N1
M1
Q1
P1
N2
M2
Q2
P2
M1N1//P1Q1
M2N2//P2Q2
M3N3//P3Q3
AD//BC
相等
相等
相等
a
b
结论:夹在两条平行线间的平行线段相等。
N3
M3
Q3
P3
两条平行中,一条直线任意一点到另一条直线的距离,叫做这两条平行线之间的距离。
A
B
直线a上所有点到直线b上的距离都相等。
结论:夹在两条平行线间的平行线段相等。
a
b
N3
M3
Q3
P3
A
B
a
b
a//b,A是a上任意一点,且AB⊥b,B是垂足,线段AB的长就是a,b之间的距离。
两条平行线中,一条直线任意一点到另一条直线的距离,叫做这两条平行线之间的距离。
点点
点线
线线(两条平行线)
1.如图,l1∥l2,则△ABC与△DBC的面积的关系是 (填“相等”或“不相等”),理由是这两个三角形同底等高,根据 ,可知这两个三角形的高相等.
2.如图
ABCD中,
ABP的面积S,
ADP,
BCP
则S与S1+S2的大小关系是_ __
面积分别是S1,S2,
B
P
D
C
A
S1
S
S2
3.如图,P为 ABCD内任一点,△PAB,△PBC,△PCD的面积分别为3,4,5,则△PAD的面积为 .
4.如图,在 ABCD中,E是BC边上一点,且AB=AE.求证:DE=AC.
5.
课堂小结
18.1.1 平行四边形的性质
知 识
1、平行四边形定义
2、平行四边形的性质
3、夹在两条平行线 间的平行线段相等。
4、平行线间的距离
思 想
转化
四边形
三角形
转化思想
方 法
验证
观察
猜想
探索新知识
证明线段相等的方法
学以致用
里面每同一方向木条都互相平行但并不均匀,
里面每一同方向木条都均匀分布且互相平行,
有一等腰三角形的木格子(如图),
你能帮木工师傅算出拼木格子所需木条的总长度吗? (不计接头).
已知等腰三角形的腰长是30cm,底边长是50cm,
C
A
B
3.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,移动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
A
B
C
D
思考:回忆以前,我们是按照怎样的思路来研究三角形的呢?
一般三角形
等腰三角形
等边三角形
直角三角形
特殊三角形
定义
性质
判定
四边形
平行四边形
应用
伸缩门
找一找
从下面的图片中,试着找出你熟悉的图形。
瓷砖图案
楼梯护栏
平行四边形
汽车车标
18.1.1 平行四边形(1)
两组对边分别平行的四边形叫做平行四边形.
一、平行四边形的定义
A
B
C
D
1、符号表示:
用 ,如图记作: ABCD,读作“平行四边形ABCD”。
2、对边:AB与CD,AD与BC
对角: ∠A与∠C, ∠B与∠D
邻角: ∠A与∠B, ∠C与∠D等
对角线:线段 AC和线段BD
观察平行四边形,你能不能猜想出
平行四边形的对边之间有什么特殊的关系?
对角之间又有什么特殊的关系?
邻角之间又有什么特殊的关系?
二、平行四边形的性质
A
B
C
D
A
B
C
D
四边形ABCD是平行四边形
(1)AB=CD,AD=CB(2)∠A=∠C,∠B=∠D.
已知:
求证:
平行四边形的对边相等,对角相等。
四边形
问题
三角形
问题
转化
证明
猜想
观察
性质1 平行四边形的对边相等。
性质2 平行四边形的对角相等。
A
B
C
D
思考:你觉得求平行四边形的边长或角,需要什么已知条件?
1.如图是某区部分街道示意图,其中BC∥AD∥EG,AB//FH∥DC.图中的平行四边形共有_____个.
9
A
B
C
D
E
G
F
H
O
从B站乘车到D站只有两
条路线有直接到达的公交车,
路线1是B—E—A—F—D,
路线2是B—H—O—G—D,
请比较两条路线路程的长短,
并说明理由.
三、平行四边形的性质的应用
2.
3.如图, ABCD 中,DE⊥AB,BF⊥CD,
垂足分别为E,F.求证:AE=CF.
A
B
C
D
E
F
A
B
C
D
E
F
a
b
AD与BC
对边
相等
N1
M1
Q1
P1
N2
M2
Q2
P2
N3
M3
Q3
P3
M1N1//P1Q1
M2N2//P2Q2
M3N3//P3Q3
AD//BC
相等
相等
相等
结论:夹在两条平行线间的平行线段相等。
a
b
N3
M3
Q3
P3
结论:夹在两条平行线间的平行线段相等。
A
B
C
D
AD与BC
对边
相等
N1
M1
Q1
P1
N2
M2
Q2
P2
M1N1//P1Q1
M2N2//P2Q2
M3N3//P3Q3
AD//BC
相等
相等
相等
a
b
结论:夹在两条平行线间的平行线段相等。
N3
M3
Q3
P3
两条平行中,一条直线任意一点到另一条直线的距离,叫做这两条平行线之间的距离。
A
B
直线a上所有点到直线b上的距离都相等。
结论:夹在两条平行线间的平行线段相等。
a
b
N3
M3
Q3
P3
A
B
a
b
a//b,A是a上任意一点,且AB⊥b,B是垂足,线段AB的长就是a,b之间的距离。
两条平行线中,一条直线任意一点到另一条直线的距离,叫做这两条平行线之间的距离。
点点
点线
线线(两条平行线)
1.如图,l1∥l2,则△ABC与△DBC的面积的关系是 (填“相等”或“不相等”),理由是这两个三角形同底等高,根据 ,可知这两个三角形的高相等.
2.如图
ABCD中,
ABP的面积S,
ADP,
BCP
则S与S1+S2的大小关系是_ __
面积分别是S1,S2,
B
P
D
C
A
S1
S
S2
3.如图,P为 ABCD内任一点,△PAB,△PBC,△PCD的面积分别为3,4,5,则△PAD的面积为 .
4.如图,在 ABCD中,E是BC边上一点,且AB=AE.求证:DE=AC.
5.
课堂小结
18.1.1 平行四边形的性质
知 识
1、平行四边形定义
2、平行四边形的性质
3、夹在两条平行线 间的平行线段相等。
4、平行线间的距离
思 想
转化
四边形
三角形
转化思想
方 法
验证
观察
猜想
探索新知识
证明线段相等的方法
学以致用
里面每同一方向木条都互相平行但并不均匀,
里面每一同方向木条都均匀分布且互相平行,
有一等腰三角形的木格子(如图),
你能帮木工师傅算出拼木格子所需木条的总长度吗? (不计接头).
已知等腰三角形的腰长是30cm,底边长是50cm,
C
A
B
3.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,移动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
A
B
C
D
