人教版九年级上册 23.1 图形的旋转 课件(共24张PPT)
文档属性
| 名称 | 人教版九年级上册 23.1 图形的旋转 课件(共24张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
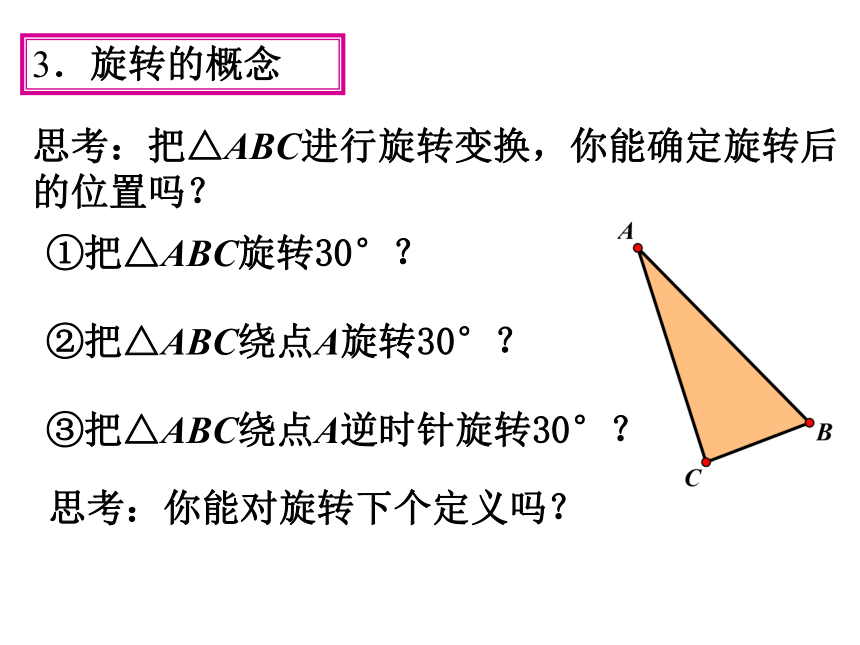
回忆:
我们学过哪些图形变换?
1.温故知新
图形变换:①平移变换②轴对称变换③旋转变换
.
.
2.生活中的旋转
23.1图形的旋转
3.旋转的概念
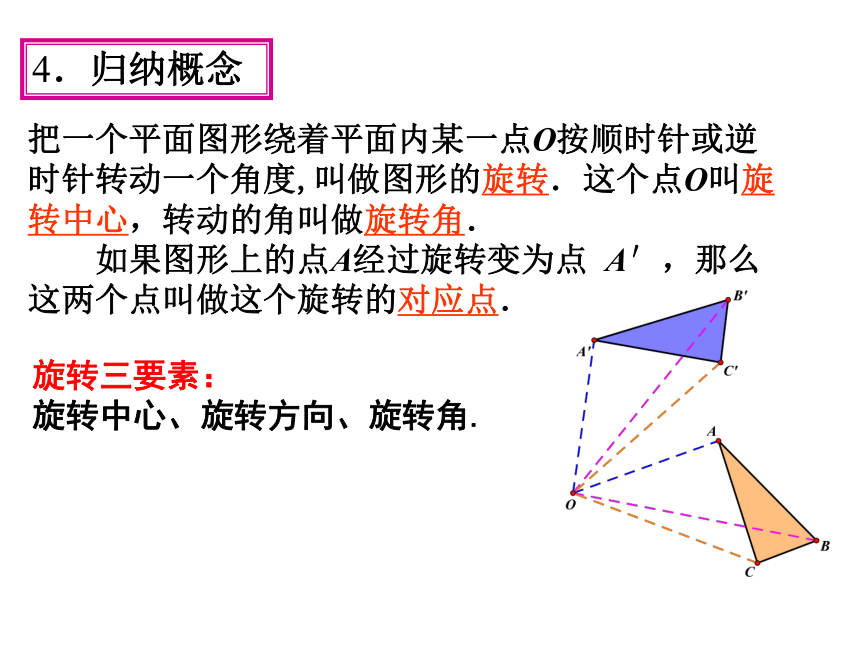
思考:把△ABC进行旋转变换,你能确定旋转后的位置吗?
①把△ABC旋转30°?
②把△ABC绕点A旋转30°?
③把△ABC绕点A逆时针旋转30°?
思考:你能对旋转下个定义吗?
4.归纳概念
把一个平面图形绕着平面内某一点O按顺时针或逆时针转动一个角度,叫做图形的旋转.这个点O叫旋转中心,转动的角叫做旋转角.
如果图形上的点A经过旋转变为点 A′,那么这两个点叫做这个旋转的对应点.
旋转三要素:
旋转中心、旋转方向、旋转角.
旋转的研究思路:
旋转的定义
旋转的性质
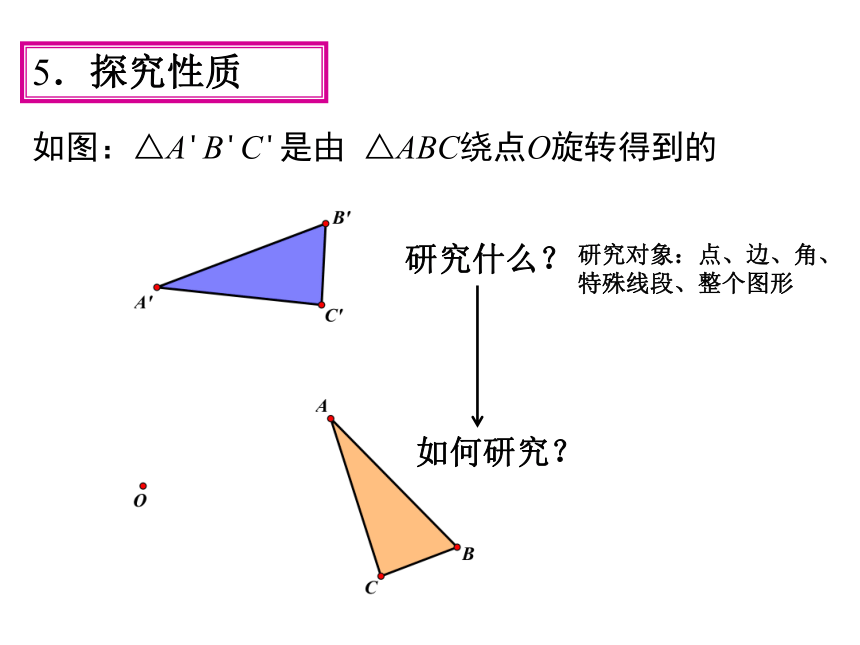
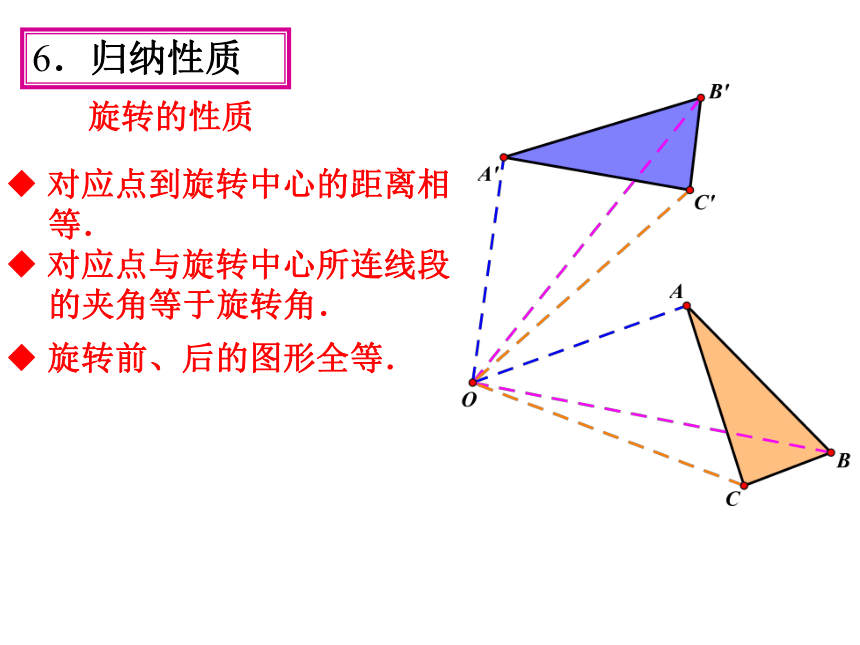
如图:△A'B'C'是由 △ABC绕点O旋转得到的
5.探究性质
研究什么?
如何研究?
研究对象:点、边、角、特殊线段、整个图形
6.归纳性质
◆ 对应点到旋转中心的距离相等.
◆ 对应点与旋转中心所连线段的夹角等于旋转角.
◆ 旋转前、后的图形全等.
旋转的性质
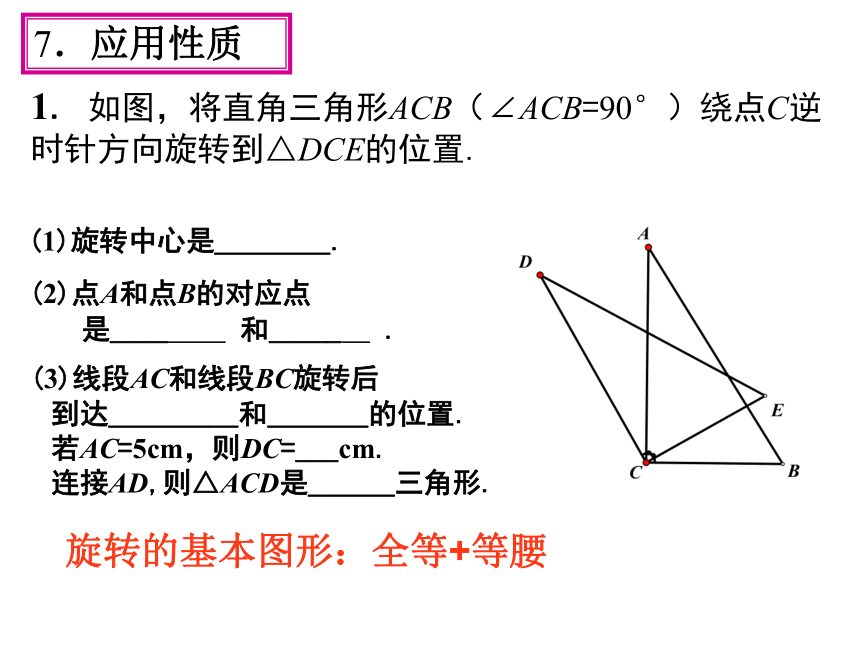
(3)线段AC和线段BC旋转后
到达_________和_______的位置.
若AC=5cm,则DC=___cm.
连接AD,则△ACD是______三角形.
1. 如图,将直角三角形ACB(∠ACB=90°)绕点C逆时针方向旋转到△DCE的位置.
(1)旋转中心是________.
(2)点A和点B的对应点
是____ 和_____ .
7.应用性质
旋转的基本图形:全等+等腰
(4)∠A和∠B旋转后
到_____和_____的位置.
旋转角为_____ 和______.
若∠ACD=30°,则∠BCE=___°.
连接AD,若∠ACD=60°,
则△ACD为______三角形
对应线段所在直线的夹角等于旋转角
1. 如图,将直角三角形ACB(∠ACB=90°)绕点C逆时针方向旋转到△DCE的位置.
线段AB与线段DE的夹角等于?
A
B
C
D
E
2. 如图,E是正方形ABCD边CD上任意一点,以A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
(要求写出作法并说明作法依据)
7.应用性质
分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置
变式1:如图, E 是正方形 ABCD 中 CD 边上任意一
点,以点 A 为中心,把 △ADE
A
B
C
E
D
顺时针
旋转 90°,你能
画出旋转后的图形吗?
变式1:如图, E 是正方形 ABCD 中 CD 边上任意一
点,以点 A 为中心,把 △ADE
旋转 90°,你能
画出旋转后的图形吗?
变式2:如果正方形ABCD的两边BA,BC分别在x轴上、y轴上,点E (5, 3)在边CD上,以A为中心,把 △ADE 旋转 90°,则旋转后点E的对应点的坐标是——
x
y
如果正方形ABCD的两边BA,BC分别在x轴上、y轴上,点E (5, 3)在边CD上,以A为中心,把 △ADE 旋转 90°,则旋转后点E的对应点的坐标为——
变式3:如果把平面直角坐标系的原点移动到A上,点E坐标为(5,-2),点H与点F的坐标分别是什么?
x
y
关于原点对称点的坐标
3.如图,矩形ABCD,AD=3,AB=5,将矩形ABCD绕着顶点B顺时针旋转,得到矩形EBGF,顶点A、D、C分别与点E、F、G对应(点D与点F不重合).如果点E在CD上,求线段AE的长 .
旋转的基本图形:全等+等腰
变式:如图,矩形ABCD,AD=a,将矩形ABCD绕着顶点B顺时针旋转,得到矩形EBGF,顶点A、D、C分别与点E、F、G对应(点D与点F不重合).如果点D、E、F在同一条直线上,求线段DF的长 .(用含a的代数式表示)
旋转的基本图形:全等+等腰
图形变换
小结:对比平移、轴对称,旋转的性质,它们有哪些相同点和不同点?
三要素
三性质
全
等
变
换
中心对称
图案设计
中心对称图形
关于原点对称的点的坐标
轴对称
平移
旋转
小结反思,回顾展望
类比
我们知道图形在旋转过程中,自身的形状和大小是不会变化的。其实生活亦然,当你为生活的山重水复而愁眉苦脸时,我们不妨旋转一个角度看世界,相信你一定会收获一个柳暗花明的美好心情。
悟旋转
7.分层作业
必做题: P60第5题和第8题
选做题:如图∠ADC=∠B=90°,DE⊥AB,E为AB上的一点,且AD=CD,DE=5.请求出四边形ABCD的面积.
A
B
C
D
E
回忆:
我们学过哪些图形变换?
1.温故知新
图形变换:①平移变换②轴对称变换③旋转变换
.
.
2.生活中的旋转
23.1图形的旋转
3.旋转的概念
思考:把△ABC进行旋转变换,你能确定旋转后的位置吗?
①把△ABC旋转30°?
②把△ABC绕点A旋转30°?
③把△ABC绕点A逆时针旋转30°?
思考:你能对旋转下个定义吗?
4.归纳概念
把一个平面图形绕着平面内某一点O按顺时针或逆时针转动一个角度,叫做图形的旋转.这个点O叫旋转中心,转动的角叫做旋转角.
如果图形上的点A经过旋转变为点 A′,那么这两个点叫做这个旋转的对应点.
旋转三要素:
旋转中心、旋转方向、旋转角.
旋转的研究思路:
旋转的定义
旋转的性质
如图:△A'B'C'是由 △ABC绕点O旋转得到的
5.探究性质
研究什么?
如何研究?
研究对象:点、边、角、特殊线段、整个图形
6.归纳性质
◆ 对应点到旋转中心的距离相等.
◆ 对应点与旋转中心所连线段的夹角等于旋转角.
◆ 旋转前、后的图形全等.
旋转的性质
(3)线段AC和线段BC旋转后
到达_________和_______的位置.
若AC=5cm,则DC=___cm.
连接AD,则△ACD是______三角形.
1. 如图,将直角三角形ACB(∠ACB=90°)绕点C逆时针方向旋转到△DCE的位置.
(1)旋转中心是________.
(2)点A和点B的对应点
是____ 和_____ .
7.应用性质
旋转的基本图形:全等+等腰
(4)∠A和∠B旋转后
到_____和_____的位置.
旋转角为_____ 和______.
若∠ACD=30°,则∠BCE=___°.
连接AD,若∠ACD=60°,
则△ACD为______三角形
对应线段所在直线的夹角等于旋转角
1. 如图,将直角三角形ACB(∠ACB=90°)绕点C逆时针方向旋转到△DCE的位置.
线段AB与线段DE的夹角等于?
A
B
C
D
E
2. 如图,E是正方形ABCD边CD上任意一点,以A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
(要求写出作法并说明作法依据)
7.应用性质
分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置
变式1:如图, E 是正方形 ABCD 中 CD 边上任意一
点,以点 A 为中心,把 △ADE
A
B
C
E
D
顺时针
旋转 90°,你能
画出旋转后的图形吗?
变式1:如图, E 是正方形 ABCD 中 CD 边上任意一
点,以点 A 为中心,把 △ADE
旋转 90°,你能
画出旋转后的图形吗?
变式2:如果正方形ABCD的两边BA,BC分别在x轴上、y轴上,点E (5, 3)在边CD上,以A为中心,把 △ADE 旋转 90°,则旋转后点E的对应点的坐标是——
x
y
如果正方形ABCD的两边BA,BC分别在x轴上、y轴上,点E (5, 3)在边CD上,以A为中心,把 △ADE 旋转 90°,则旋转后点E的对应点的坐标为——
变式3:如果把平面直角坐标系的原点移动到A上,点E坐标为(5,-2),点H与点F的坐标分别是什么?
x
y
关于原点对称点的坐标
3.如图,矩形ABCD,AD=3,AB=5,将矩形ABCD绕着顶点B顺时针旋转,得到矩形EBGF,顶点A、D、C分别与点E、F、G对应(点D与点F不重合).如果点E在CD上,求线段AE的长 .
旋转的基本图形:全等+等腰
变式:如图,矩形ABCD,AD=a,将矩形ABCD绕着顶点B顺时针旋转,得到矩形EBGF,顶点A、D、C分别与点E、F、G对应(点D与点F不重合).如果点D、E、F在同一条直线上,求线段DF的长 .(用含a的代数式表示)
旋转的基本图形:全等+等腰
图形变换
小结:对比平移、轴对称,旋转的性质,它们有哪些相同点和不同点?
三要素
三性质
全
等
变
换
中心对称
图案设计
中心对称图形
关于原点对称的点的坐标
轴对称
平移
旋转
小结反思,回顾展望
类比
我们知道图形在旋转过程中,自身的形状和大小是不会变化的。其实生活亦然,当你为生活的山重水复而愁眉苦脸时,我们不妨旋转一个角度看世界,相信你一定会收获一个柳暗花明的美好心情。
悟旋转
7.分层作业
必做题: P60第5题和第8题
选做题:如图∠ADC=∠B=90°,DE⊥AB,E为AB上的一点,且AD=CD,DE=5.请求出四边形ABCD的面积.
A
B
C
D
E
同课章节目录
