人教版九年级上册 第二十三章 旋转 复习课件(共32张PPT)
文档属性
| 名称 | 人教版九年级上册 第二十三章 旋转 复习课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 00:00:00 | ||
图片预览

文档简介
(共32张PPT)
旋 转 复 习 课
A
B
C
C′
A′
B′
O
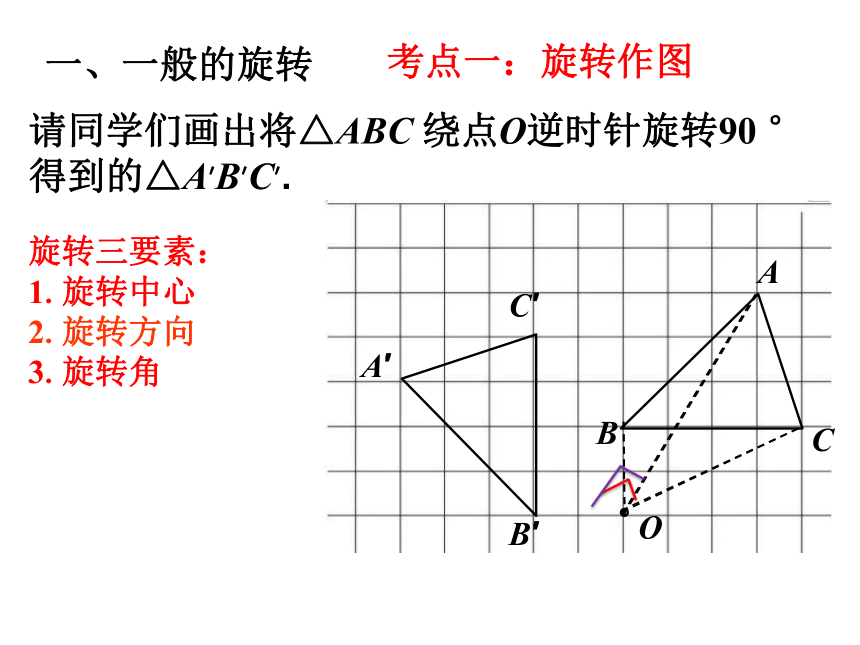
请同学们画出将△ABC 绕点O逆时针旋转90 °得到的△A′B′C′.
旋转三要素:
1.旋转中心
2.旋转方向
3.旋转角
一、一般的旋转
考点一:旋转作图
A
B
C
C′
A′
B′
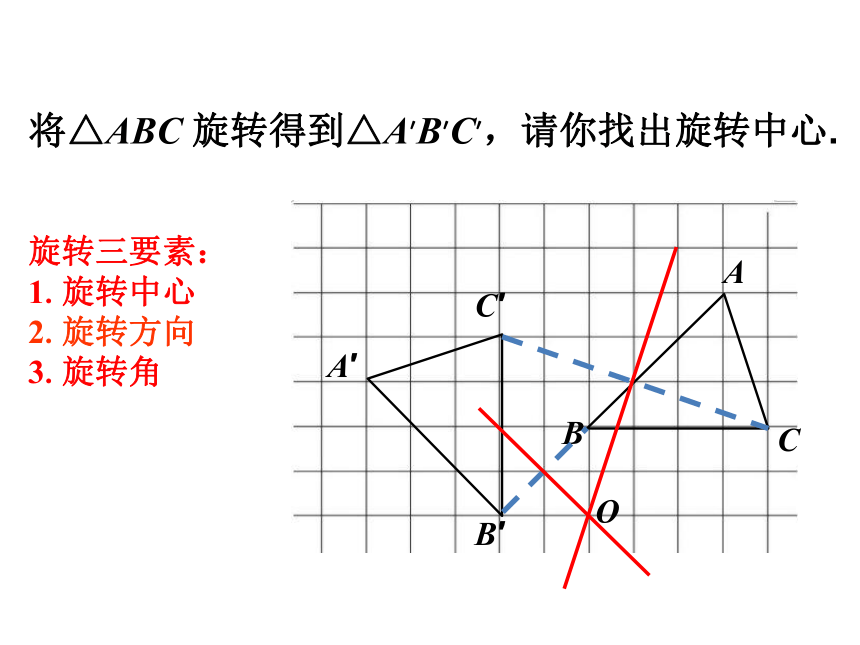
将△ABC 旋转得到△A′B′C′,请你找出旋转中心.
旋转三要素:
1.旋转中心
2.旋转方向
3.旋转角
O
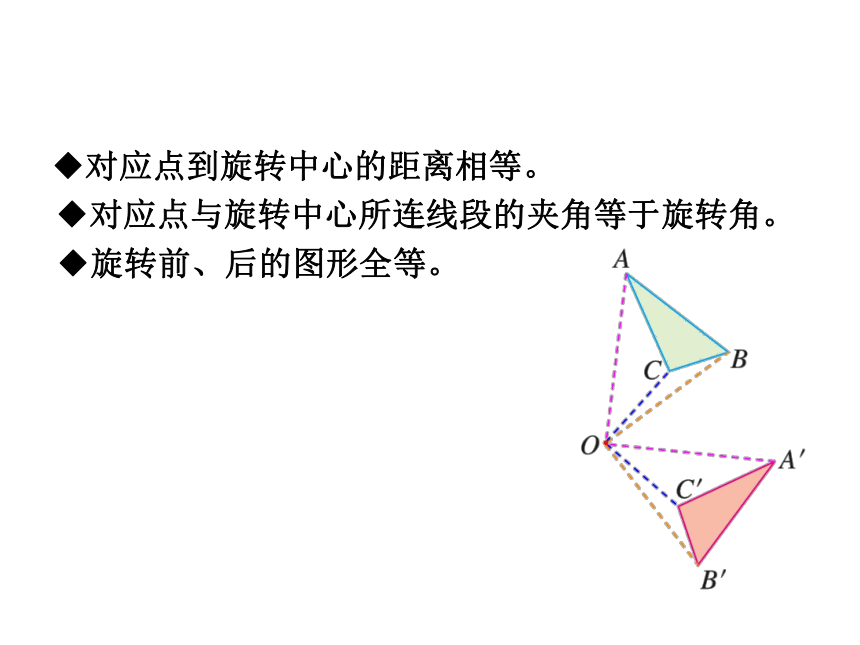
◆旋转前、后的图形全等。
◆对应点到旋转中心的距离相等。
◆对应点与旋转中心所连线段的夹角等于旋转角。
旋转的基本性质
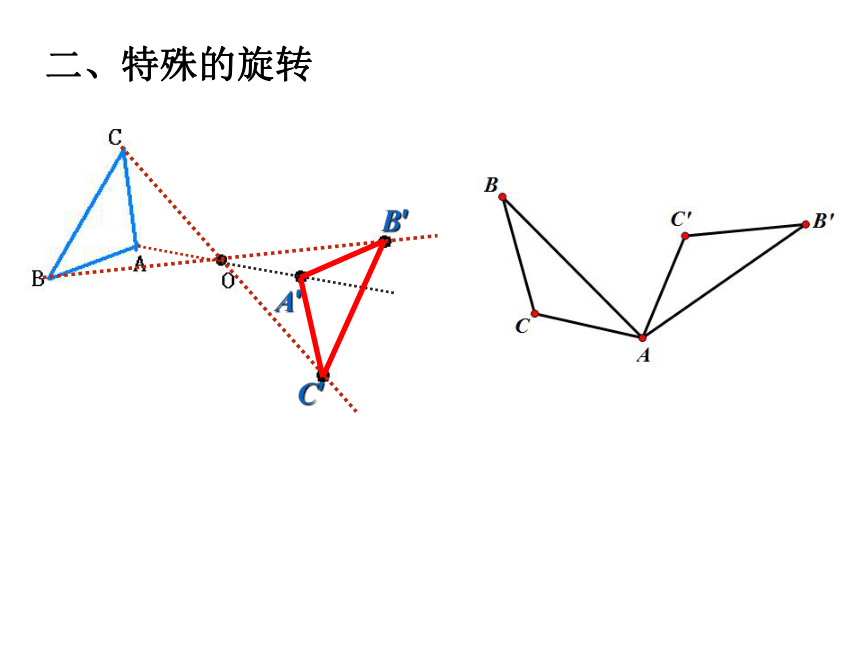
二、特殊的旋转
A′
C′
B′
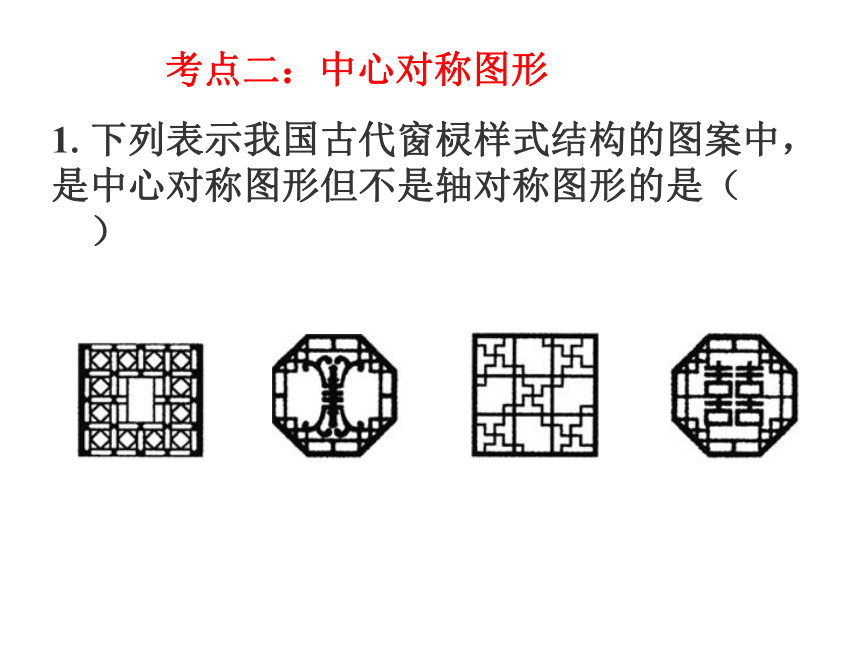
1.下列表示我国古代窗棂样式结构的图案中,是中心对称图形但不是轴对称图形的是( )
考点二:中心对称图形
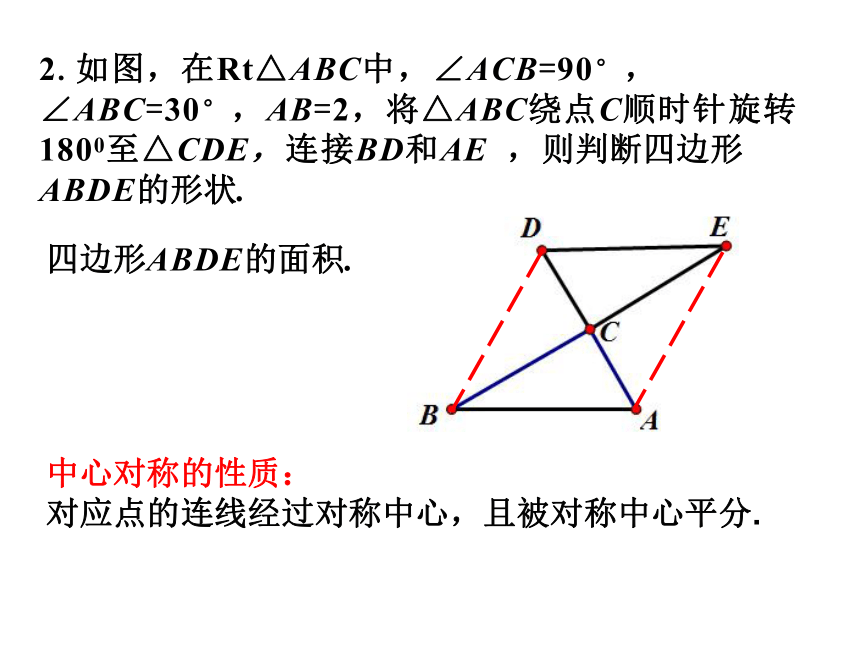
2.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=2,将△ABC绕点C顺时针旋转1800至△CDE,连接BD和AE ,则判断四边形ABDE的形状.
中心对称的性质:
对应点的连线经过对称中心,且被对称中心平分.
四边形ABDE的面积.
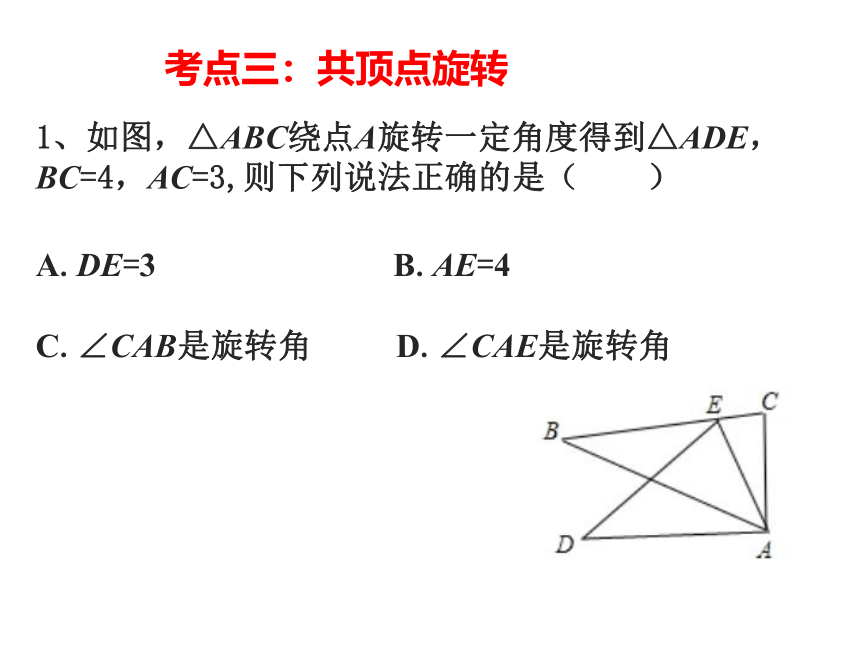
1、如图,△ABC绕点A旋转一定角度得到△ADE,BC=4,AC=3,则下列说法正确的是( )
A.DE=3 B.AE=4
C.∠CAB是旋转角 D.∠CAE是旋转角
考点三:共顶点旋转
复习旧知·检测反馈
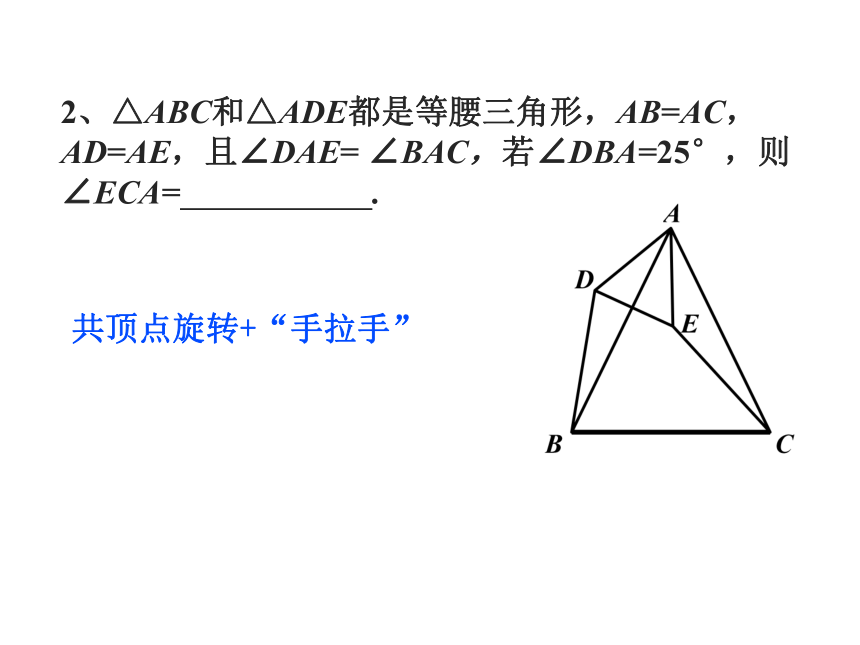
2、△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠DAE= ∠BAC,若∠DBA=25°,则∠ECA= .
共顶点旋转+“手拉手”
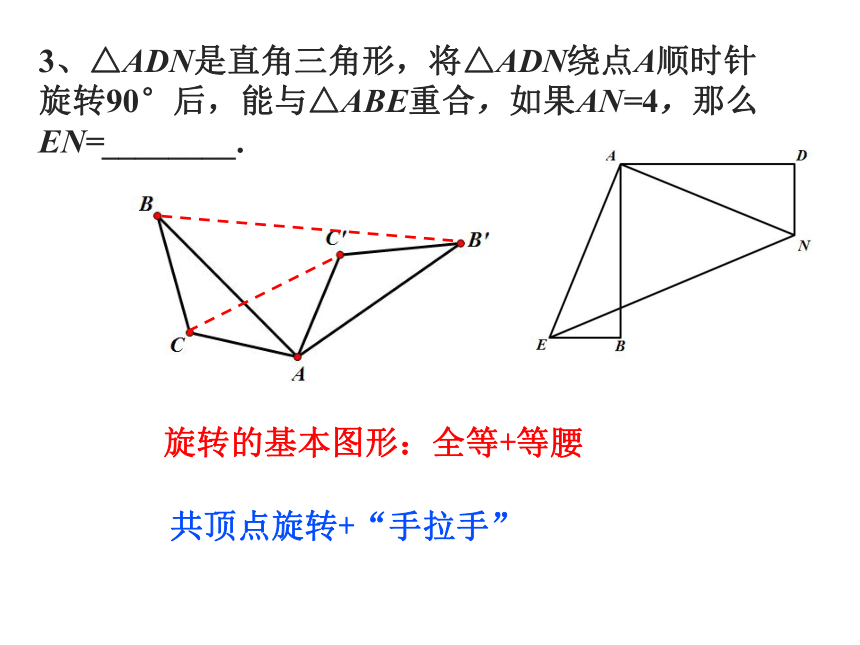
3、△ADN是直角三角形,将△ADN绕点A顺时针旋转90°后,能与△ABE重合,如果AN=4,那么EN=________.
旋转的基本图形:全等+等腰
共顶点旋转+“手拉手”
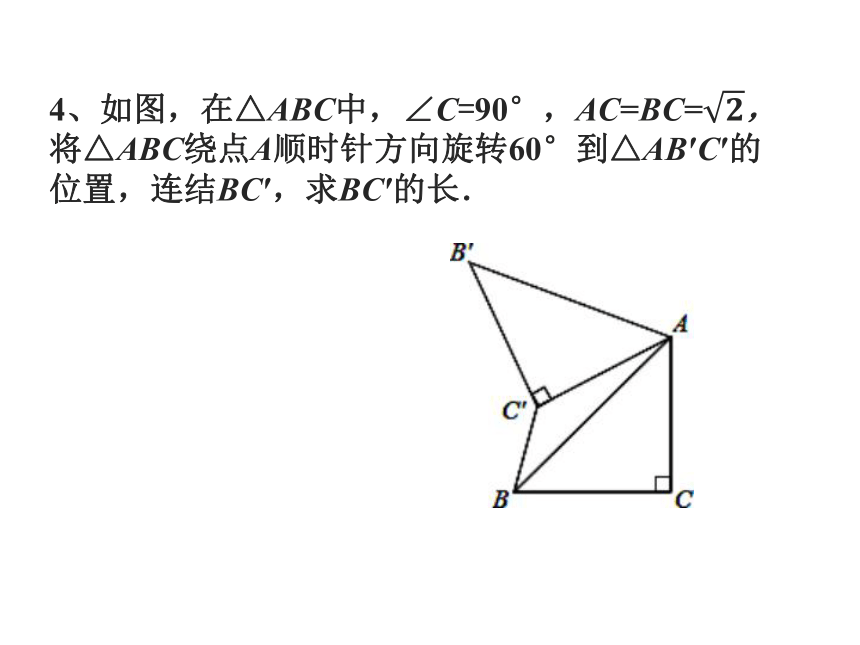
4、如图,在△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连结BC′,求BC′的长.
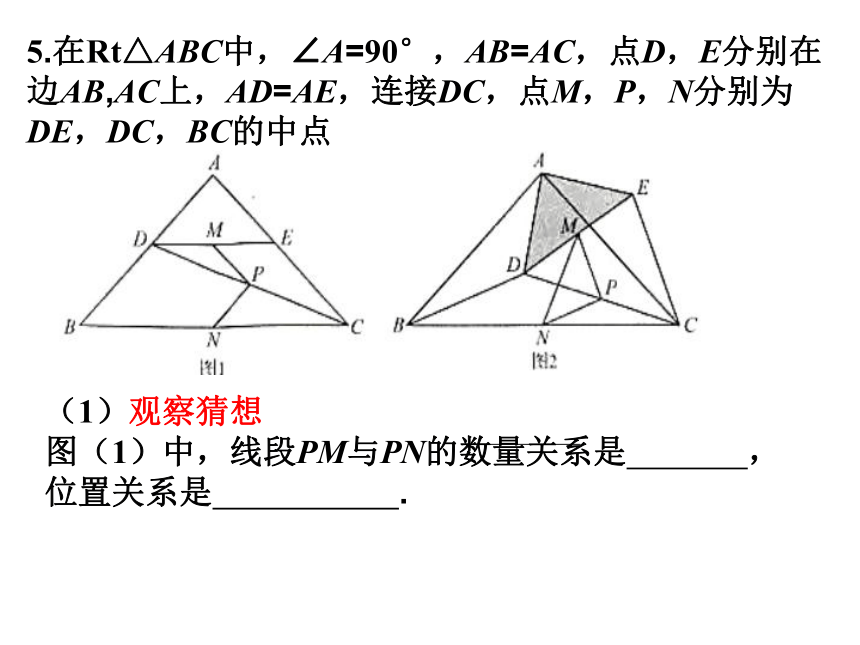
(1)观察猜想
图(1)中,线段PM与PN的数量关系是 ,位置关系是 .
5.在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点
(2)探究证明
把△ADE绕点A逆时针旋转到图(2)的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由。
5.在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点
5.在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
如图,四边形ABCD为正方形,AB=1,把△ABC绕点A逆时针旋转60°得到△AEF,连接DF,则DF的长为( )
求BF的长度
B
A
两张矩形纸片ABCD和CEFG完全相同,且AB=CE,AD>AB.
操作发现:
(1)如图1,点D在GC上,连接AC、CF、CG、AG,则AC和CF有何数量关系和位置关系?并说明理由.
实践探究:
(2)如图2,将图1中的纸片CEFG以点C为旋转中心逆时针旋转,当点D落在GE上时停止旋转,则AG和GF在同一条直线上吗?请判断,并说明理由.
1、如图,在正方形ABCD中,∠MAN=45°,当∠MAN绕点A顺时针旋转到如图的位置时,它的两边分别交BC,DC于点M,N,线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
半角模型
旋转法
典例重温
操作探究
猜想:BM+DN=MN
证明:延长CB至点N',使________,连接AN'
∵四边形ABCD是正方形
∴AB=AD,∠ABC=∠D=90°∴∠ABN'=90°
在△ABN'和△ADN中,
∴△ABN'≌△ADN(______),
∴AN'=AN,∠1=∠____,
∵∠BAD=90°,∠MAN=45°,
∴∠2+∠3=____°,∴∠1+∠3=____°,
∴∠N'AM=∠NAM,
在△AN'M和△ANM中,
∴△AN'M≌△ANM(____),
∴MN'=MN,
又MN'=BN'+BM=DN+BM,
∴BM+DN=MN
如图,正方形ABCD中,∠MAN=45°,
∠MAN的两边分别交BD于点M,N.
延长CD至点M',使DM'=BM,连接AM',
下列结论:
①AM=AM' ②∠NAM'=∠NAM
③ BM+DN=MN ④AN=AM,
其中正确的是:
A. ①② B.②④ C.①②③ D.①④
组织交流·释疑拓展
变式教学·检测反馈
2、如图,正方形ABCD中,∠MAN=45°,当∠MAN绕点A顺时针旋转到如图的位置时,它的两边分别交CB,DC的延长线于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
变式
1
如图,正方形ABCD中,∠MAN=45°,当∠MAN绕点A逆时针旋转到如图的位置时,它的两边分别交BC,CD的延长线于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
变式
2
变式教学·检测反馈
归纳总结·拓展提升
5、如图,在四边形ABCD中, ,
∠MAN的两边分别交CB,DC于点M,N.
要使BM+DN=MN.还需要添加哪些条件?
变式
3
归纳总结·拓展提升
半角模型
变式1
变式2
从特殊到一般
转化思想
变式3
半角模型的条件:
1、半角
2、邻边相等
3、对角互补
例1、如图,P是正三角形ABC内一点,PA=6,PB=8,PC=10,若三角形PAC绕点A逆时针旋转后,得到三角形P/AB,则P与P’之间的距离为 ,∠APB= .
典例重温
求△PBC的面积
【变式】
点P是正△ ABC内部一点,∠APB=150°,∠APC=120°,PA=10,
求PB,PC的长和△ABC的边长。
如图,点P是正方形ABCD内一点,连接AP并延长,交BC于点Q.连接DP.将△ADP绕点A顺时针旋转90°至△ABP'.连结PP',若AP=1,PB= ,PD= ,则正方形的边长为( )
如图,已知∠MON=30°,B为OM上一点,BA⊥ON于点A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连接BE,若AB=2,则BE的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AB=2,点D为线段AB的中点,将线段BC绕点B顺时针旋转90°,得到线段BE,连接DE,则DE最大值是 .
如图,四边形ABCD是菱形,AB=2,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为 .
云端补救·布置作业
1、登录“家校帮”,观看课堂实录,进行
复习,完成推送的思考题,并在线完
成课后检测题。
2、完成学案上的练习。
注意什么
“变”中找“不变”
旋 转 复 习 课
A
B
C
C′
A′
B′
O
请同学们画出将△ABC 绕点O逆时针旋转90 °得到的△A′B′C′.
旋转三要素:
1.旋转中心
2.旋转方向
3.旋转角
一、一般的旋转
考点一:旋转作图
A
B
C
C′
A′
B′
将△ABC 旋转得到△A′B′C′,请你找出旋转中心.
旋转三要素:
1.旋转中心
2.旋转方向
3.旋转角
O
◆旋转前、后的图形全等。
◆对应点到旋转中心的距离相等。
◆对应点与旋转中心所连线段的夹角等于旋转角。
旋转的基本性质
二、特殊的旋转
A′
C′
B′
1.下列表示我国古代窗棂样式结构的图案中,是中心对称图形但不是轴对称图形的是( )
考点二:中心对称图形
2.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=2,将△ABC绕点C顺时针旋转1800至△CDE,连接BD和AE ,则判断四边形ABDE的形状.
中心对称的性质:
对应点的连线经过对称中心,且被对称中心平分.
四边形ABDE的面积.
1、如图,△ABC绕点A旋转一定角度得到△ADE,BC=4,AC=3,则下列说法正确的是( )
A.DE=3 B.AE=4
C.∠CAB是旋转角 D.∠CAE是旋转角
考点三:共顶点旋转
复习旧知·检测反馈
2、△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠DAE= ∠BAC,若∠DBA=25°,则∠ECA= .
共顶点旋转+“手拉手”
3、△ADN是直角三角形,将△ADN绕点A顺时针旋转90°后,能与△ABE重合,如果AN=4,那么EN=________.
旋转的基本图形:全等+等腰
共顶点旋转+“手拉手”
4、如图,在△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连结BC′,求BC′的长.
(1)观察猜想
图(1)中,线段PM与PN的数量关系是 ,位置关系是 .
5.在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点
(2)探究证明
把△ADE绕点A逆时针旋转到图(2)的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由。
5.在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点
5.在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
如图,四边形ABCD为正方形,AB=1,把△ABC绕点A逆时针旋转60°得到△AEF,连接DF,则DF的长为( )
求BF的长度
B
A
两张矩形纸片ABCD和CEFG完全相同,且AB=CE,AD>AB.
操作发现:
(1)如图1,点D在GC上,连接AC、CF、CG、AG,则AC和CF有何数量关系和位置关系?并说明理由.
实践探究:
(2)如图2,将图1中的纸片CEFG以点C为旋转中心逆时针旋转,当点D落在GE上时停止旋转,则AG和GF在同一条直线上吗?请判断,并说明理由.
1、如图,在正方形ABCD中,∠MAN=45°,当∠MAN绕点A顺时针旋转到如图的位置时,它的两边分别交BC,DC于点M,N,线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
半角模型
旋转法
典例重温
操作探究
猜想:BM+DN=MN
证明:延长CB至点N',使________,连接AN'
∵四边形ABCD是正方形
∴AB=AD,∠ABC=∠D=90°∴∠ABN'=90°
在△ABN'和△ADN中,
∴△ABN'≌△ADN(______),
∴AN'=AN,∠1=∠____,
∵∠BAD=90°,∠MAN=45°,
∴∠2+∠3=____°,∴∠1+∠3=____°,
∴∠N'AM=∠NAM,
在△AN'M和△ANM中,
∴△AN'M≌△ANM(____),
∴MN'=MN,
又MN'=BN'+BM=DN+BM,
∴BM+DN=MN
如图,正方形ABCD中,∠MAN=45°,
∠MAN的两边分别交BD于点M,N.
延长CD至点M',使DM'=BM,连接AM',
下列结论:
①AM=AM' ②∠NAM'=∠NAM
③ BM+DN=MN ④AN=AM,
其中正确的是:
A. ①② B.②④ C.①②③ D.①④
组织交流·释疑拓展
变式教学·检测反馈
2、如图,正方形ABCD中,∠MAN=45°,当∠MAN绕点A顺时针旋转到如图的位置时,它的两边分别交CB,DC的延长线于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
变式
1
如图,正方形ABCD中,∠MAN=45°,当∠MAN绕点A逆时针旋转到如图的位置时,它的两边分别交BC,CD的延长线于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
变式
2
变式教学·检测反馈
归纳总结·拓展提升
5、如图,在四边形ABCD中, ,
∠MAN的两边分别交CB,DC于点M,N.
要使BM+DN=MN.还需要添加哪些条件?
变式
3
归纳总结·拓展提升
半角模型
变式1
变式2
从特殊到一般
转化思想
变式3
半角模型的条件:
1、半角
2、邻边相等
3、对角互补
例1、如图,P是正三角形ABC内一点,PA=6,PB=8,PC=10,若三角形PAC绕点A逆时针旋转后,得到三角形P/AB,则P与P’之间的距离为 ,∠APB= .
典例重温
求△PBC的面积
【变式】
点P是正△ ABC内部一点,∠APB=150°,∠APC=120°,PA=10,
求PB,PC的长和△ABC的边长。
如图,点P是正方形ABCD内一点,连接AP并延长,交BC于点Q.连接DP.将△ADP绕点A顺时针旋转90°至△ABP'.连结PP',若AP=1,PB= ,PD= ,则正方形的边长为( )
如图,已知∠MON=30°,B为OM上一点,BA⊥ON于点A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连接BE,若AB=2,则BE的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AB=2,点D为线段AB的中点,将线段BC绕点B顺时针旋转90°,得到线段BE,连接DE,则DE最大值是 .
如图,四边形ABCD是菱形,AB=2,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为 .
云端补救·布置作业
1、登录“家校帮”,观看课堂实录,进行
复习,完成推送的思考题,并在线完
成课后检测题。
2、完成学案上的练习。
注意什么
“变”中找“不变”
同课章节目录
