人教版七年级下册 5.1.1 相交线 课件(共15张PPT)
文档属性
| 名称 | 人教版七年级下册 5.1.1 相交线 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 244.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 09:30:46 | ||
图片预览




文档简介
(共15张PPT)
5.1 相交线
(第一课时)
问题 两条直线有哪些位置关系?
请同学们在纸上任意画两条直线.
动手操作
问题驱动 激活思维
一
平行
垂直
相交
文字格式:
1.文字均为“宋体,28号,黑色,加粗”;
2.字母用“Times New Roman,斜体,28号,黑色,加粗”;
3.段落首起空两个字,行距根据内容调整。
问题驱动 激活思维
一
平行线
相交线
两条直线相交产生的角的关系
两条直线被第三条直线所截产生的角的关系
平行公理
平移
性质
判定
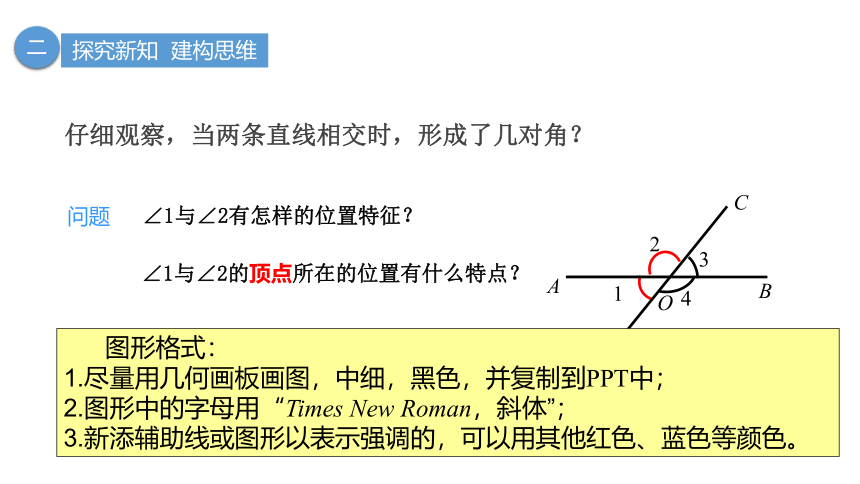
∠1与∠2的顶点所在的位置有什么特点?
∠1与∠2的边所在的位置有什么特点?
问题
仔细观察,当两条直线相交时,形成了几对角?
A
B
C
D
O
1
2
3
4
探究新知 建构思维
二
∠1与∠2有怎样的位置特征?
图形格式:
1.尽量用几何画板画图,中细,黑色,并复制到PPT中;
2.图形中的字母用“Times New Roman,斜体”;
3.新添辅助线或图形以表示强调的,可以用其他红色、蓝色等颜色。
邻补角
∠1和∠2有一条公共边OA,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角.
A
B
C
D
O
1
2
3
4
图中共有几对邻补角?
问题
∠1和∠4
∠2和∠3
∠3和∠4
探究新知 建构思维
二
∠1和∠2
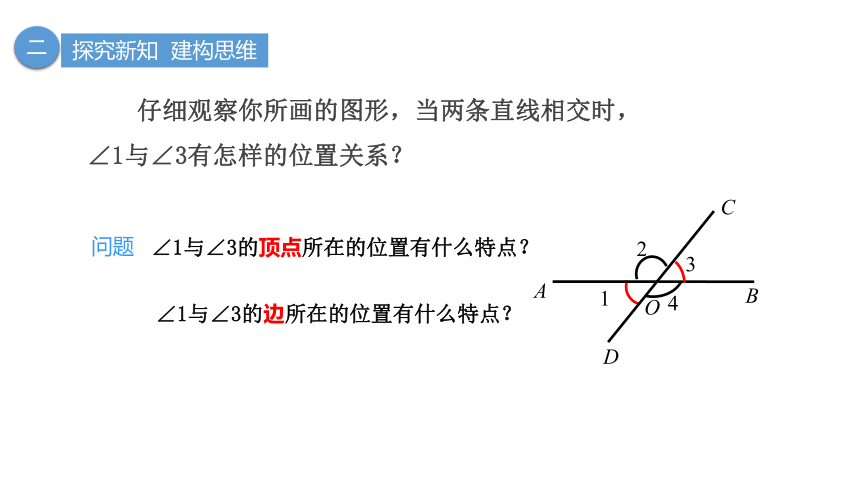
仔细观察你所画的图形,当两条直线相交时,∠1与∠3有怎样的位置关系?
A
B
C
D
O
1
2
3
4
∠1与∠3的顶点所在的位置有什么特点?
∠1与∠3的边所在的位置有什么特点?
问题
探究新知 建构思维
二
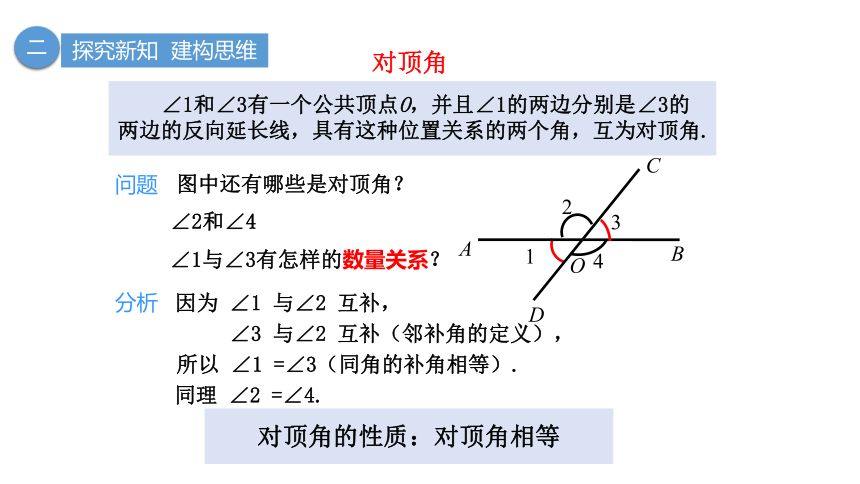
对顶角
图中还有哪些是对顶角?
问题
∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
A
B
C
D
O
1
2
3
4
∠1与∠3有怎样的数量关系?
∠2和∠4
因为 ∠1 与∠2 互补,
分析
探究新知 建构思维
二
对顶角的性质:对顶角相等
∠3 与∠2 互补(邻补角的定义),
所以 ∠1 =∠3(同角的补角相等).
同理 ∠2 =∠4.
对顶角相等
探究新知 建构思维
二
1
2
3
4
a
b
对顶角
邻补角
∠1和∠4
∠2和∠3
∠3和∠4
∠1和∠2
∠2和∠4
∠1和∠3
邻补角互补
如图,直线a,b相交,∠1 = 40°,求∠2,∠3,∠4的度数.
例
1
2
3
4
a
b
由邻补角定义,可得
解
∠2=180°-∠1=180°-40°=140°,
例
题
演
练
应用迁移 拓展思维
三
由对顶角相等,
所以 ∠3=∠1=40°,
所以 ∠4=∠2=140°.
解答格式:
1.题目文字均为“宋体,24号,黑色,加粗”;
1.解答文字均为“仿宋,24号,黑色,,加粗”;
2.字母用“Times New Roman,斜体,24号,黑色,加粗”;
3.解答段落首起空两个字,行距根据内容调整,不能太密;
4.“解”的格式为“蓝色,微软雅黑,24号”,后面空一个字。
1.若∠1 +∠3 = 80°,求∠1 、∠2、∠3、∠4的度数.
1
2
3
4
a
b
如图,直线a,b相交.
变式
所以∠1=∠3=40°,
所以∠1+∠3=2∠1=80°,
所以∠2=∠4=180°- 40 =140°.
解
由对顶角相等,得∠1=∠3,
例
题
演
练
应用迁移 拓展思维
三
2.若∠2是∠1的3.5倍,求∠1 、∠2、∠3、∠4的度数.
1
2
3
4
a
b
如图,直线a,b相交.
变式
所以∠1=∠3=40°,
所以∠1+∠2=∠1+3.5∠1=180°,
所以∠2=∠4=180°-40 =140°.
解
由邻补角定义,得∠1+∠2=180°,
例
题
演
练
应用迁移 拓展思维
三
3.若 1 : 2 = 2 :7 ,求∠1 、∠2、∠3、∠4的度数.
1
2
3
4
a
b
如图,直线a,b相交.
变式
解
由邻补角定义,得∠1+∠2=180°,
因为 1 : 2 = 2 :7,设 1=2x, 2=7x.
所以x=20°,
巧用方程思想
例
题
演
练
应用迁移 拓展思维
三
所以∠1+∠2=2x+7x=180°,
所以∠1=∠3=40°,
所以∠2=∠4=180°-40 =140°.
已知一个角求另外三个角
已知两个角的关系求角的度数
某综合实践小组利用两根木条a、b,将它们钉在一起,探究今天的学习内容,首先固定木条a,转动木条b.
(1)当a与b所成锐角α为35°时,其余的角分别为多少?
(2)当a与b所成角α为90°时,其余的角分别为多少?
(3)当a与b所成角α为m°时,其余的角分别为多少?
应用迁移 拓展思维
三
生
长
拓
学
m°,(180-m)°,(180-m)°
特殊
一般
该综合实践小组深入探究,发现多条直线交于一点,对顶角数量有
一定规律,观察下列各图,寻找对顶角(不含平角).
(1)如图a,图中共有 对对顶角;
(2)如图b,图中共有 对对顶角;
(3)如图c,图中共有 对对顶角;
(4)研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,
猜测:若有n条直线相交于一点,则可形成 对对顶角;
(5)若有10条直线相交于一点,则可形成 对对顶角.
图c
2
6
12
n(n-1)
90
图a
A
B
C
D
O
图b
A
B
C
D
E
F
O
A
B
C
D
E
F
G
H
O
特殊
一般
应用迁移 拓展思维
三
生
长
拓
学
1×2=2
2×3=6
3×4=12
2条
3条
4条
对顶角
相交线
邻补角
相同点
1
2
3
4
a
b
①都是两条直线相交而成的角;
②都有一个公共顶点;
③都是成对出现的.
①有无公共边;
②两直线相交时,对顶角只有
两对,邻补角有四对.
不同点
梳理小结 深化思维
四
小学
七上
七下
基本平面图形——直线、射线、线段和角
两条直线相交
两条直线平行
初步认识几何图形
特殊
一般
方程思想
5.1 相交线
(第一课时)
问题 两条直线有哪些位置关系?
请同学们在纸上任意画两条直线.
动手操作
问题驱动 激活思维
一
平行
垂直
相交
文字格式:
1.文字均为“宋体,28号,黑色,加粗”;
2.字母用“Times New Roman,斜体,28号,黑色,加粗”;
3.段落首起空两个字,行距根据内容调整。
问题驱动 激活思维
一
平行线
相交线
两条直线相交产生的角的关系
两条直线被第三条直线所截产生的角的关系
平行公理
平移
性质
判定
∠1与∠2的顶点所在的位置有什么特点?
∠1与∠2的边所在的位置有什么特点?
问题
仔细观察,当两条直线相交时,形成了几对角?
A
B
C
D
O
1
2
3
4
探究新知 建构思维
二
∠1与∠2有怎样的位置特征?
图形格式:
1.尽量用几何画板画图,中细,黑色,并复制到PPT中;
2.图形中的字母用“Times New Roman,斜体”;
3.新添辅助线或图形以表示强调的,可以用其他红色、蓝色等颜色。
邻补角
∠1和∠2有一条公共边OA,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角.
A
B
C
D
O
1
2
3
4
图中共有几对邻补角?
问题
∠1和∠4
∠2和∠3
∠3和∠4
探究新知 建构思维
二
∠1和∠2
仔细观察你所画的图形,当两条直线相交时,∠1与∠3有怎样的位置关系?
A
B
C
D
O
1
2
3
4
∠1与∠3的顶点所在的位置有什么特点?
∠1与∠3的边所在的位置有什么特点?
问题
探究新知 建构思维
二
对顶角
图中还有哪些是对顶角?
问题
∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
A
B
C
D
O
1
2
3
4
∠1与∠3有怎样的数量关系?
∠2和∠4
因为 ∠1 与∠2 互补,
分析
探究新知 建构思维
二
对顶角的性质:对顶角相等
∠3 与∠2 互补(邻补角的定义),
所以 ∠1 =∠3(同角的补角相等).
同理 ∠2 =∠4.
对顶角相等
探究新知 建构思维
二
1
2
3
4
a
b
对顶角
邻补角
∠1和∠4
∠2和∠3
∠3和∠4
∠1和∠2
∠2和∠4
∠1和∠3
邻补角互补
如图,直线a,b相交,∠1 = 40°,求∠2,∠3,∠4的度数.
例
1
2
3
4
a
b
由邻补角定义,可得
解
∠2=180°-∠1=180°-40°=140°,
例
题
演
练
应用迁移 拓展思维
三
由对顶角相等,
所以 ∠3=∠1=40°,
所以 ∠4=∠2=140°.
解答格式:
1.题目文字均为“宋体,24号,黑色,加粗”;
1.解答文字均为“仿宋,24号,黑色,,加粗”;
2.字母用“Times New Roman,斜体,24号,黑色,加粗”;
3.解答段落首起空两个字,行距根据内容调整,不能太密;
4.“解”的格式为“蓝色,微软雅黑,24号”,后面空一个字。
1.若∠1 +∠3 = 80°,求∠1 、∠2、∠3、∠4的度数.
1
2
3
4
a
b
如图,直线a,b相交.
变式
所以∠1=∠3=40°,
所以∠1+∠3=2∠1=80°,
所以∠2=∠4=180°- 40 =140°.
解
由对顶角相等,得∠1=∠3,
例
题
演
练
应用迁移 拓展思维
三
2.若∠2是∠1的3.5倍,求∠1 、∠2、∠3、∠4的度数.
1
2
3
4
a
b
如图,直线a,b相交.
变式
所以∠1=∠3=40°,
所以∠1+∠2=∠1+3.5∠1=180°,
所以∠2=∠4=180°-40 =140°.
解
由邻补角定义,得∠1+∠2=180°,
例
题
演
练
应用迁移 拓展思维
三
3.若 1 : 2 = 2 :7 ,求∠1 、∠2、∠3、∠4的度数.
1
2
3
4
a
b
如图,直线a,b相交.
变式
解
由邻补角定义,得∠1+∠2=180°,
因为 1 : 2 = 2 :7,设 1=2x, 2=7x.
所以x=20°,
巧用方程思想
例
题
演
练
应用迁移 拓展思维
三
所以∠1+∠2=2x+7x=180°,
所以∠1=∠3=40°,
所以∠2=∠4=180°-40 =140°.
已知一个角求另外三个角
已知两个角的关系求角的度数
某综合实践小组利用两根木条a、b,将它们钉在一起,探究今天的学习内容,首先固定木条a,转动木条b.
(1)当a与b所成锐角α为35°时,其余的角分别为多少?
(2)当a与b所成角α为90°时,其余的角分别为多少?
(3)当a与b所成角α为m°时,其余的角分别为多少?
应用迁移 拓展思维
三
生
长
拓
学
m°,(180-m)°,(180-m)°
特殊
一般
该综合实践小组深入探究,发现多条直线交于一点,对顶角数量有
一定规律,观察下列各图,寻找对顶角(不含平角).
(1)如图a,图中共有 对对顶角;
(2)如图b,图中共有 对对顶角;
(3)如图c,图中共有 对对顶角;
(4)研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,
猜测:若有n条直线相交于一点,则可形成 对对顶角;
(5)若有10条直线相交于一点,则可形成 对对顶角.
图c
2
6
12
n(n-1)
90
图a
A
B
C
D
O
图b
A
B
C
D
E
F
O
A
B
C
D
E
F
G
H
O
特殊
一般
应用迁移 拓展思维
三
生
长
拓
学
1×2=2
2×3=6
3×4=12
2条
3条
4条
对顶角
相交线
邻补角
相同点
1
2
3
4
a
b
①都是两条直线相交而成的角;
②都有一个公共顶点;
③都是成对出现的.
①有无公共边;
②两直线相交时,对顶角只有
两对,邻补角有四对.
不同点
梳理小结 深化思维
四
小学
七上
七下
基本平面图形——直线、射线、线段和角
两条直线相交
两条直线平行
初步认识几何图形
特殊
一般
方程思想
