正方形的性质[下学期]
图片预览







文档简介
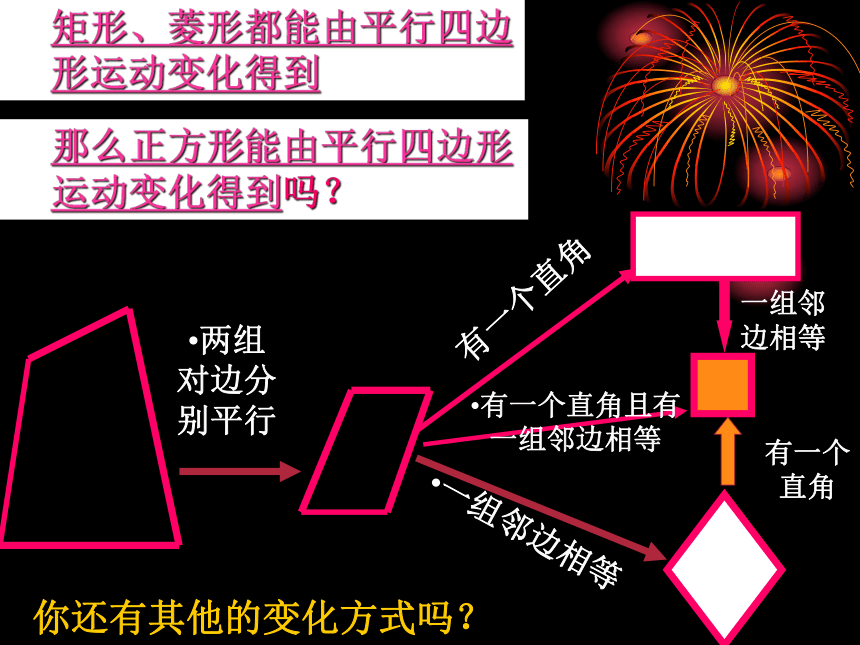
课件23张PPT。正方形的性质两组对边分别平行有一个直角一组邻边相等有一个直角且有一组邻边相等矩形、菱形都能由平行四边形运动变化得到那么正方形能由平行四边形运动变化得到吗?你还有其他的变化方式吗?一组邻边相等有一个直角正方形定义
(类似于矩形、菱形)有一个直角且有一组邻边相等的平行四边形叫做正方形(1)正方形的三个要点:
a: 是平行四边形
b: 有一个角是直角
c: 有一组邻边相等(2)对比正方形与矩形.菱形的定义,得出联系
a:由正方形的定义可知正方形是特殊的矩形
b:由正方形的定义可知正方形是特殊的菱形
c:由正方形的定义可知正方形又是特殊的平行四边形
d:平行四边形,矩形,菱形,正方形都是特殊的四边形
正方形既是 又是矩形菱形观察下列集合图,你能得出什么结论?平行四边形矩形菱形正方形4.从整体知识结构出发,研究正方形的性质边对角线对边平行四边相等对角线相等 互相垂直平分每条对角线平分一组对角四个角相等且都是直角角正方形性质正方形具有平行四边形、矩形、菱形的一切性质。轴对称图形
4条对称轴对称性的研究轴对称图形
2条对称轴轴对称图形
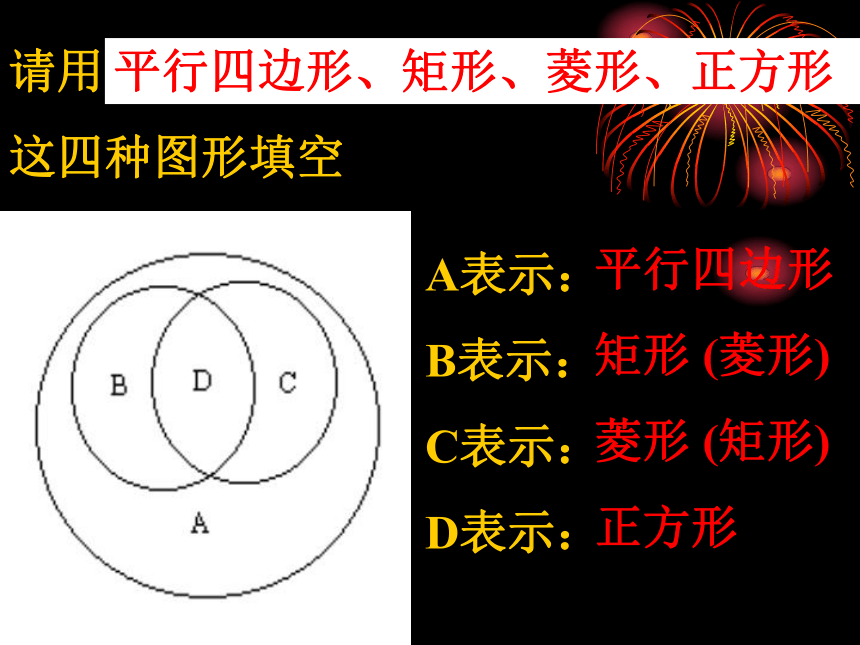
2条对称轴你能有什么规律?请用
这四种图形填空A表示:
B表示:
C表示:
D表示:平行四边形
矩形 (菱形)
菱形 (矩形)
正方形平行四边形、矩形、菱形、正方形已知:正方形的一条对角线长为4cm 解:∵四边形ABCD是正方形
∴AB = BC,∠ABC=90°
﹙正方形的四个角都是直角,四条边都相等﹚1、正方形的面积等于边长的平方。
2、正方形的面积等于等于对角线的平方的一半。
3、正方形的周长等于边长的4倍。 在Rt⊿ABC中,求: 它的边长和面积。已知:在正方形ABCD中,E、F分别在
BC、DC 上,且BE = DF,AC与BC
相交于O点,EF 与AC相交于P点
求证:EF ⊥ AC,EF ∥ BD∴ EF ∥ BD证明: ∵四边形ABCD是正方形∴BC = CD∵BE = DF∴EC = FC∵AC平分∠BCD ∴EF⊥ AC∵AC ⊥BD二.正方形的性质的应用例1 如图:正方形ABCD中,
A D
B C
(1)一条对角线把它分成_____个全等的________三角形
(2)两条对角线把它分成_______个全等的________三角形
2等腰直角4等腰直角(3)对角线AC与正方形的一边所成的角为_____度
(4)正方形的面积为64cm2,求正方形的对角线长及
对角线交点o到正方形一边的距离_______
(5) AB: AO: AC=________ 45AD:1:2小结:
1、正方形的定义。
2、平行四边形、矩形、菱形和正方形的关系。
3、正方形的性质。
4、正方形的周长、面积的求法。例2求证:正方形的两条对角线把正方形分成四个全等的 等腰直角三角形。 已知:四边形ABCD是正方形,对角
线AC、BD相交于点O
求证:⊿ABO、 ⊿ BCO 、 ⊿ CDO、
⊿ DAO是全等的等腰直角三角形 证明:∵四边形ABCD是正方形 由于正方形的面积等于⊿ABO 面积的4倍,所以正方形的面积等于对角线的平方的一半。∴AC=BD,AC⊥BD,AO = CO = BO = DO
﹙正方形的对角线相等,并且互相垂直平分﹚∴⊿ABO、 ⊿ BCO 、 ⊿ CDO、 ⊿ DAO 都是等腰直角三角形,并且⊿ABO ≌⊿ BCO ≌ ⊿ CDO ≌ ⊿ DAO已知:如图2-28,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F.求证:EC=EF=FB. 例2 如图,在正方形ABCD中,E,F分别是CD和AD上的点,EF=AF+CE.求角EBF的度数
例1已知正方形ABCD,延长AB到E,连结EC,作AG⊥EC于G,AG交BC于F,求证:AF=CE例2
如图,正方形ABCD,P为对角线BD上一点,
试说明:PA=PCABCDP例2.如图,在正方形ABCD中,E在BC的延长线上,且CE=AC,AE交CD于F,则求∠AFC的度数。练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF 证明: 例3:如图,边长为a的正方形ABCD的对角线AC,BD相交于点O,E,F分别为DC,BC上的点,且DE=CF。
求证: (1)EO垂直OF
(2)M ,N分别在OE,OF延长线上且
OM=ON=a,正方形MONG与
正方形ABCD重合部分的面积等于1 / 4a
1、已知:如图,在正方形ABCD中,E是CF上一点,四边形BEFD是菱形。求角BEF的度数补充题:ABCDEF2、已知:如图:在正方形
ABDE和ACFG中,
MN过点A垂直BC于N,
交EG于M。求证:M为EG中点
a: 是平行四边形
b: 有一个角是直角
c: 有一组邻边相等(2)对比正方形与矩形.菱形的定义,得出联系
a:由正方形的定义可知正方形是特殊的矩形
b:由正方形的定义可知正方形是特殊的菱形
c:由正方形的定义可知正方形又是特殊的平行四边形
d:平行四边形,矩形,菱形,正方形都是特殊的四边形
正方形既是 又是矩形菱形观察下列集合图,你能得出什么结论?平行四边形矩形菱形正方形4.从整体知识结构出发,研究正方形的性质边对角线对边平行四边相等对角线相等 互相垂直平分每条对角线平分一组对角四个角相等且都是直角角正方形性质正方形具有平行四边形、矩形、菱形的一切性质。轴对称图形
4条对称轴对称性的研究轴对称图形
2条对称轴轴对称图形
2条对称轴你能有什么规律?请用
这四种图形填空A表示:
B表示:
C表示:
D表示:平行四边形
矩形 (菱形)
菱形 (矩形)
正方形平行四边形、矩形、菱形、正方形已知:正方形的一条对角线长为4cm 解:∵四边形ABCD是正方形
∴AB = BC,∠ABC=90°
﹙正方形的四个角都是直角,四条边都相等﹚1、正方形的面积等于边长的平方。
2、正方形的面积等于等于对角线的平方的一半。
3、正方形的周长等于边长的4倍。 在Rt⊿ABC中,求: 它的边长和面积。已知:在正方形ABCD中,E、F分别在
BC、DC 上,且BE = DF,AC与BC
相交于O点,EF 与AC相交于P点
求证:EF ⊥ AC,EF ∥ BD∴ EF ∥ BD证明: ∵四边形ABCD是正方形∴BC = CD∵BE = DF∴EC = FC∵AC平分∠BCD ∴EF⊥ AC∵AC ⊥BD二.正方形的性质的应用例1 如图:正方形ABCD中,
A D
B C
(1)一条对角线把它分成_____个全等的________三角形
(2)两条对角线把它分成_______个全等的________三角形
2等腰直角4等腰直角(3)对角线AC与正方形的一边所成的角为_____度
(4)正方形的面积为64cm2,求正方形的对角线长及
对角线交点o到正方形一边的距离_______
(5) AB: AO: AC=________ 45AD:1:2小结:
1、正方形的定义。
2、平行四边形、矩形、菱形和正方形的关系。
3、正方形的性质。
4、正方形的周长、面积的求法。例2求证:正方形的两条对角线把正方形分成四个全等的 等腰直角三角形。 已知:四边形ABCD是正方形,对角
线AC、BD相交于点O
求证:⊿ABO、 ⊿ BCO 、 ⊿ CDO、
⊿ DAO是全等的等腰直角三角形 证明:∵四边形ABCD是正方形 由于正方形的面积等于⊿ABO 面积的4倍,所以正方形的面积等于对角线的平方的一半。∴AC=BD,AC⊥BD,AO = CO = BO = DO
﹙正方形的对角线相等,并且互相垂直平分﹚∴⊿ABO、 ⊿ BCO 、 ⊿ CDO、 ⊿ DAO 都是等腰直角三角形,并且⊿ABO ≌⊿ BCO ≌ ⊿ CDO ≌ ⊿ DAO已知:如图2-28,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F.求证:EC=EF=FB. 例2 如图,在正方形ABCD中,E,F分别是CD和AD上的点,EF=AF+CE.求角EBF的度数
例1已知正方形ABCD,延长AB到E,连结EC,作AG⊥EC于G,AG交BC于F,求证:AF=CE例2
如图,正方形ABCD,P为对角线BD上一点,
试说明:PA=PCABCDP例2.如图,在正方形ABCD中,E在BC的延长线上,且CE=AC,AE交CD于F,则求∠AFC的度数。练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF 证明: 例3:如图,边长为a的正方形ABCD的对角线AC,BD相交于点O,E,F分别为DC,BC上的点,且DE=CF。
求证: (1)EO垂直OF
(2)M ,N分别在OE,OF延长线上且
OM=ON=a,正方形MONG与
正方形ABCD重合部分的面积等于1 / 4a
1、已知:如图,在正方形ABCD中,E是CF上一点,四边形BEFD是菱形。求角BEF的度数补充题:ABCDEF2、已知:如图:在正方形
ABDE和ACFG中,
MN过点A垂直BC于N,
交EG于M。求证:M为EG中点
