多边形的内角和与外角和[下学期]
文档属性
| 名称 | 多边形的内角和与外角和[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 215.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-19 11:46:00 | ||
图片预览




文档简介
课件25张PPT。生活中的平面图形生活中的平面图形由这图形你抽象出什么几何图形?生活中的平面图形由这图形你抽象出什么几何图形?生活中的平面图形由这图形你抽象出什么几何图形?
生活中的平面图形
由这图形你抽象出什么几何图形?生活中的平面图形
由这图形你抽象出什么几何图形?探索多边形的内角和生活中的平面图形
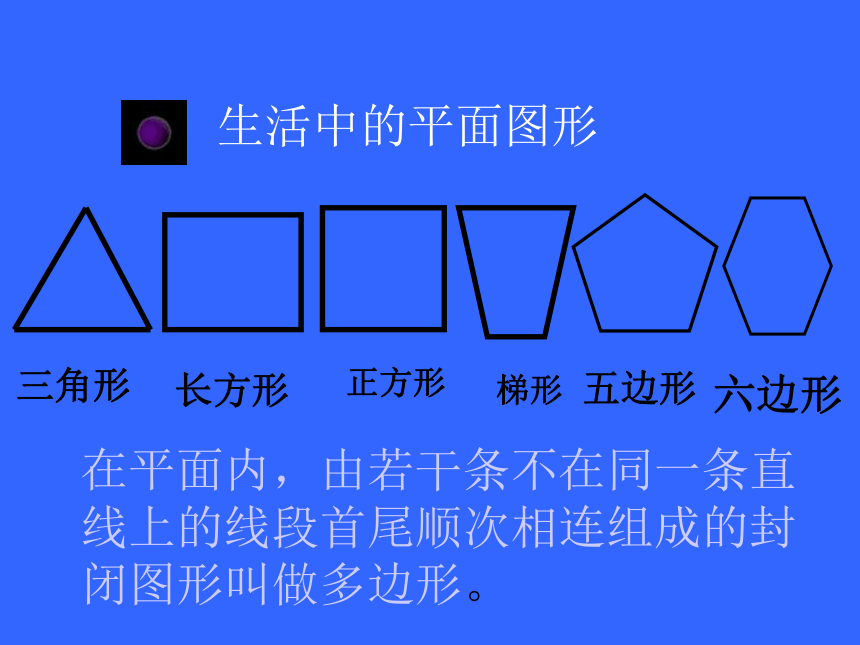
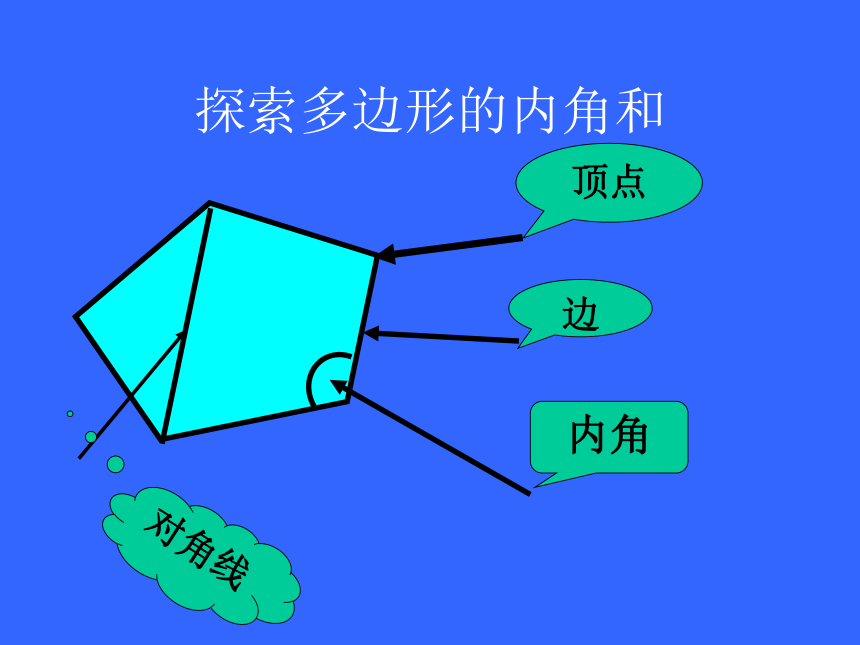
三角形 长方形 六边形在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。五边形梯形正方形探索多边形的内角和顶点边内角对角线ACB如图,三角形ABC的内角和是多少度?探索多边形的内角和探索多边形的内角和ABCD四边形的内角和是多少度?图中有几个三角形?探索多边形的内角和ABDCE 五边形的内角和是多少度?
图中有几个三角形?探索多边形的内角和ABDCFE 六边形的内角和是多少度?
图中有几个三角形?探索多边形的内角和ACDEBF这个六边形的内角和应该怎么求呢?你有几种方法呢?ACDEFB内角和=(6-2)·180°
=4 ·180°
=720 °ACDEBFO内角和=5 ·180°-180°
= 4 ·180°
=720 °ACDEBFO内角和=6 ·180°-360 °
=4 ·180°
=720 °探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-2900 °(n-2) ×180720 °540 °
例1. 已知一个多边形,它的内角和 等于720°,
求这个多边形的边数。
解: 设多边形的边数为n,因为它的内角和等于
(n-2)?180°,所以,
(n-2)?180°=720o。
解得: n=6
?这个多边形的边数为6。
例2. 已知一个多边形,它的内角和 等于五边形的 内角和的2倍,求这个多边形的边数。
解: 设多边形的边数为n,因为它的内角和等于 (n-2)?180°,
五边形内角和等于540o,所以,
(n-2)?180°=2×540o。
解得: n=8
?这个多边形的边数为8。
例3. 一个多边形当边数增加1时,它的内角和增加 多少度?
当边数增加1时,
解: 设多边形的边数为n,
因为它的内角和等于 (n-2)?180°,? (n+1-2)?180°- (n-2)?180°
=n?180°-180°-n?180°+360°
= 180°
?内角和增加180°
内角和为(n+1-2)?180°,想一想:观察下面多边形,它们的边,角有什么特点? 在平面内,内角都相等,边也都相等的多边形叫做正多边形想一想:正三角形正四边形正五边形正六边形正八边形1 上面正多边形的内角各是多少度?2 一个多边形的边都相等,它的内角一定都相等吗?反之结论成立吗?练习: 1. ( 口答) ⑴ 八边形的内角和 . ⑵如果八边形的每一个内角相等,那么每个内 角 是_________ 度。 2. 已知多边形内角和等于1080o,求它的边数。 3. 一个多边形每个内角都等于170o,求它的边数。 4、一个多边形除了一个内角之外,其余各内角之和是2570度,则这个内角的度数等于________度。4、一个多边形除了一个内角之外,其余各内角之和是2570度,则这个内角的度数等于________度。
生活中的平面图形
由这图形你抽象出什么几何图形?生活中的平面图形
由这图形你抽象出什么几何图形?探索多边形的内角和生活中的平面图形
三角形 长方形 六边形在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。五边形梯形正方形探索多边形的内角和顶点边内角对角线ACB如图,三角形ABC的内角和是多少度?探索多边形的内角和探索多边形的内角和ABCD四边形的内角和是多少度?图中有几个三角形?探索多边形的内角和ABDCE 五边形的内角和是多少度?
图中有几个三角形?探索多边形的内角和ABDCFE 六边形的内角和是多少度?
图中有几个三角形?探索多边形的内角和ACDEBF这个六边形的内角和应该怎么求呢?你有几种方法呢?ACDEFB内角和=(6-2)·180°
=4 ·180°
=720 °ACDEBFO内角和=5 ·180°-180°
= 4 ·180°
=720 °ACDEBFO内角和=6 ·180°-360 °
=4 ·180°
=720 °探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-2900 °(n-2) ×180720 °540 °
例1. 已知一个多边形,它的内角和 等于720°,
求这个多边形的边数。
解: 设多边形的边数为n,因为它的内角和等于
(n-2)?180°,所以,
(n-2)?180°=720o。
解得: n=6
?这个多边形的边数为6。
例2. 已知一个多边形,它的内角和 等于五边形的 内角和的2倍,求这个多边形的边数。
解: 设多边形的边数为n,因为它的内角和等于 (n-2)?180°,
五边形内角和等于540o,所以,
(n-2)?180°=2×540o。
解得: n=8
?这个多边形的边数为8。
例3. 一个多边形当边数增加1时,它的内角和增加 多少度?
当边数增加1时,
解: 设多边形的边数为n,
因为它的内角和等于 (n-2)?180°,? (n+1-2)?180°- (n-2)?180°
=n?180°-180°-n?180°+360°
= 180°
?内角和增加180°
内角和为(n+1-2)?180°,想一想:观察下面多边形,它们的边,角有什么特点? 在平面内,内角都相等,边也都相等的多边形叫做正多边形想一想:正三角形正四边形正五边形正六边形正八边形1 上面正多边形的内角各是多少度?2 一个多边形的边都相等,它的内角一定都相等吗?反之结论成立吗?练习: 1. ( 口答) ⑴ 八边形的内角和 . ⑵如果八边形的每一个内角相等,那么每个内 角 是_________ 度。 2. 已知多边形内角和等于1080o,求它的边数。 3. 一个多边形每个内角都等于170o,求它的边数。 4、一个多边形除了一个内角之外,其余各内角之和是2570度,则这个内角的度数等于________度。4、一个多边形除了一个内角之外,其余各内角之和是2570度,则这个内角的度数等于________度。
