小升初真题分类特训:解决问题(专项训练)-小学数学六年级下册北师大版(含答案)
文档属性
| 名称 | 小升初真题分类特训:解决问题(专项训练)-小学数学六年级下册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-09 16:55:28 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
小升初真题分类特训:解决问题(专项训练)-小学数学六年级下册北师大版
1.(2022·湖南株洲·统考小升初真题)弘毅小学从六年级任意抽取若干名学生进行体能测试,并根据收集的数据绘制成如图两幅统计图。请结合这两幅统计图提供的信息,回答下面的问题。
(1)成绩及格的有 名,优秀的有 名。
(2)六年级有多少学生参加了体能测试?
(3)请把条形统计图补充完整。
(4)请把扇形统计图缺少的信息填写完整。
2.(2022·河北唐山·统考小升初真题)今年六月份,唐山市政府助商惠民发放1.5亿消费补贴券,张阿姨领到了一张商超类消费券满360元减120元。商场正在搞八折促销活动,她买一件500元的衣服,一共可以优惠多少元?
3.(2022·河北唐山·统考小升初真题)小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸?这个笔筒的体积是多少?
4.(2022·河北唐山·统考小升初真题)妈妈把五万元钱存入银行,存期为2年,年利率为2.50%。到期时可以取回多少钱?
5.(2022·广东阳江·统考小升初真题)有一个底面直径10米,高1.8米圆柱形水池,如果在水池内壁和底面都要贴上瓷砖,这个水池贴瓷砖的面积是多少平方米?
6.(2022·广东阳江·统考小升初真题)有甲、乙两袋大米,甲袋有60千克,从甲袋取出,从乙袋取出25%后,甲、乙两袋剩余大米的质量比是8∶3。乙袋中原来有多少千克大米?
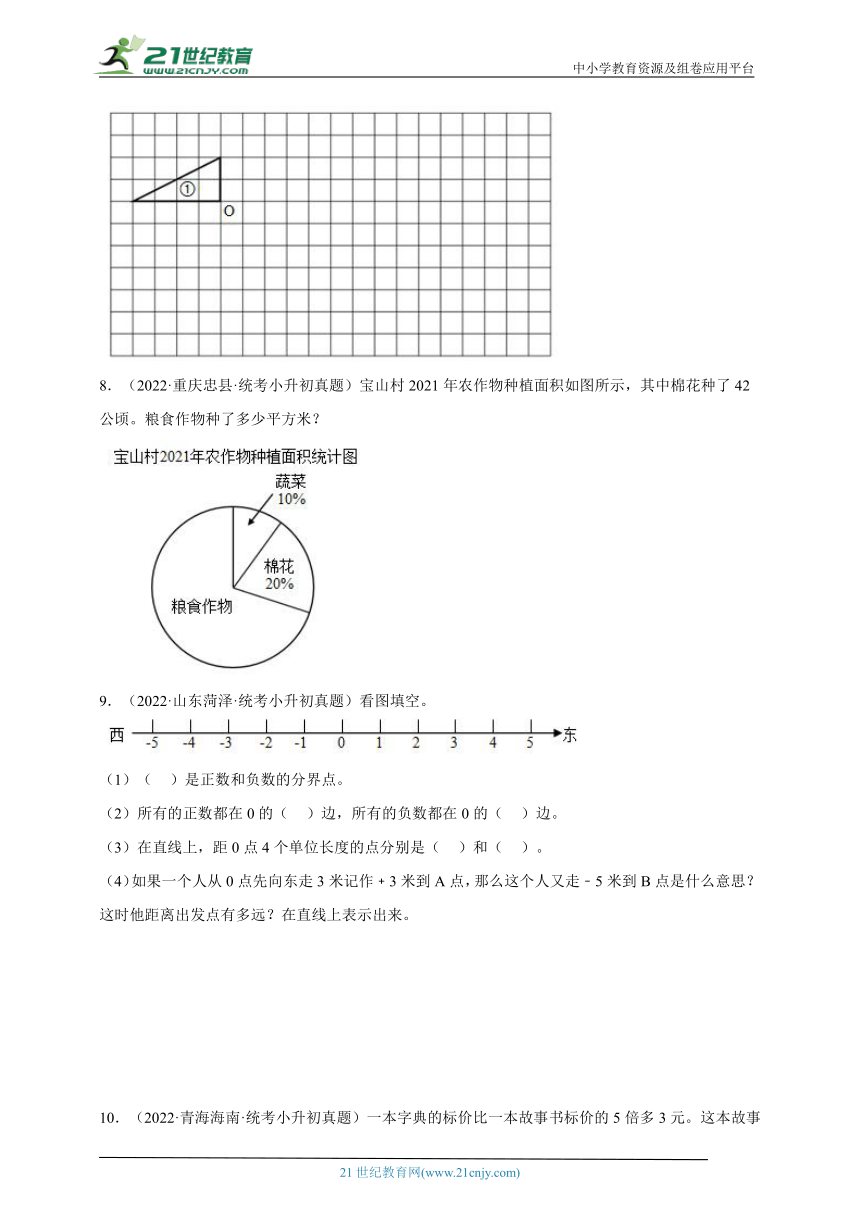
7.(2022·重庆忠县·统考小升初真题)在如图所示按要求作图。
(1)画出图①绕点O顺时针旋转90°的图,得到图②。
(2)按2∶1的比例画出图②放大后的图,得到图③。
(3)图①与图③的面积比是( )。
8.(2022·重庆忠县·统考小升初真题)宝山村2021年农作物种植面积如图所示,其中棉花种了42公顷。粮食作物种了多少平方米?
9.(2022·山东菏泽·统考小升初真题)看图填空。
(1)( )是正数和负数的分界点。
(2)所有的正数都在0的( )边,所有的负数都在0的( )边。
(3)在直线上,距0点4个单位长度的点分别是( )和( )。
(4)如果一个人从0点先向东走3米记作﹢3米到A点,那么这个人又走﹣5米到B点是什么意思?这时他距离出发点有多远?在直线上表示出来。
10.(2022·青海海南·统考小升初真题)一本字典的标价比一本故事书标价的5倍多3元。这本故事书标价5.4元,这本字典标价多少元?
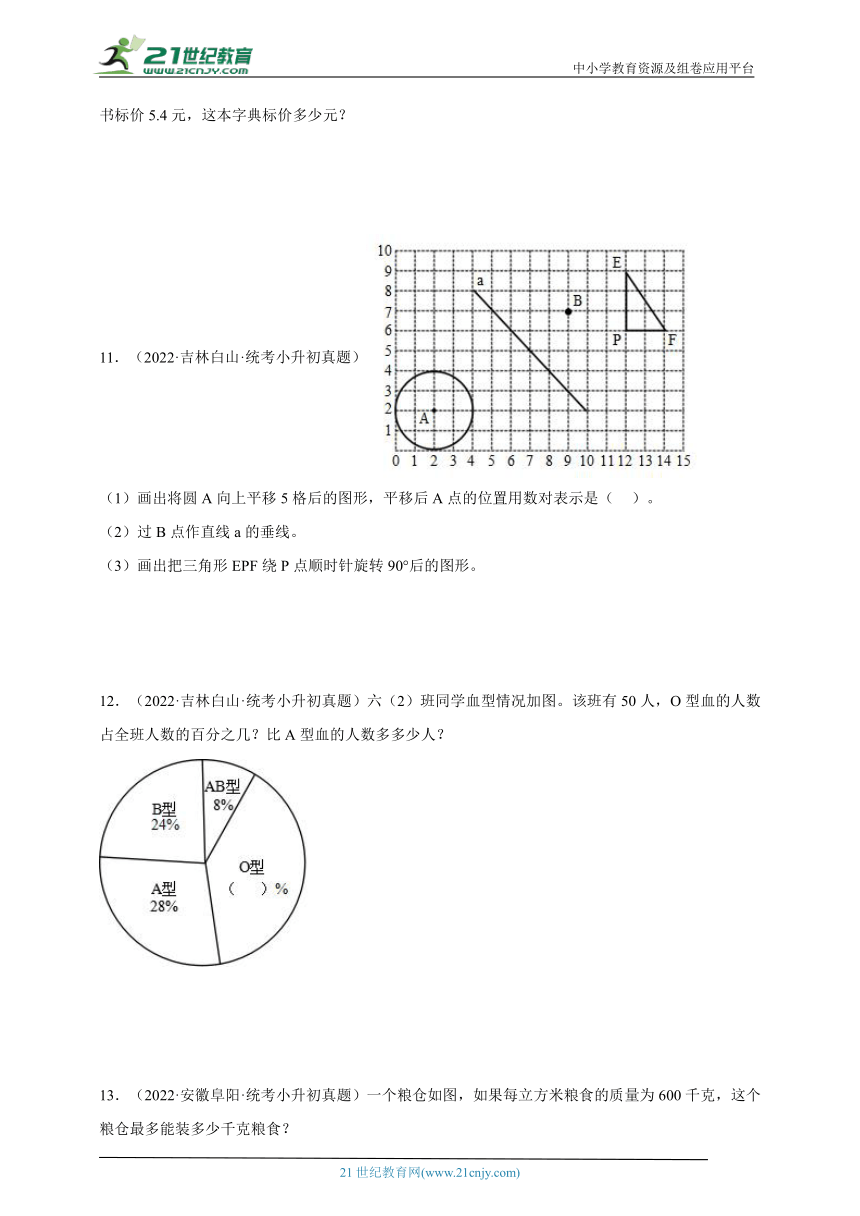
11.(2022·吉林白山·统考小升初真题)
(1)画出将圆A向上平移5格后的图形,平移后A点的位置用数对表示是( )。
(2)过B点作直线a的垂线。
(3)画出把三角形EPF绕P点顺时针旋转90°后的图形。
12.(2022·吉林白山·统考小升初真题)六(2)班同学血型情况加图。该班有50人,O型血的人数占全班人数的百分之几?比A型血的人数多多少人?
13.(2022·安徽阜阳·统考小升初真题)一个粮仓如图,如果每立方米粮食的质量为600千克,这个粮仓最多能装多少千克粮食?
14.(2022·辽宁鞍山·统考小升初真题)如图,一个内直径是6厘米的饮料瓶内饮料的高度是8厘米,将这个饮料瓶的瓶盖拧紧倒置放平,空余部分的高度是6厘米。这个饮料瓶的容积是多少毫升?
15.(2022·辽宁鞍山·统考小升初真题)学校组织老师去博物馆参展,前往博物馆,自驾车,乘公交车和步行的人数如条形统计图(部分)和扇形统计图所示。
(1)学校共有( )名老师去参展。
(2)步行前往博物馆的有( )名老师。
(3)把条形统计图补充完整。
16.(2022·福建泉州·统考小升初真题)王大伯参加了某县农村合作医疗保险。条款规定:起付400元,余下的按75%报销。今年王大伯患急性肠炎在县人民医院住院治疗9天,共计医疗费2800元。按规定王大伯自付多少元?
17.(2022·四川广安·统考小升初真题)物流公司要将一批货物运往加工厂,如果要一次把这批货物全部运出,车辆的载重量与所需车辆的数量如下表。
载重量(吨) 2.5 3 5
数量(辆) 48 40 24
(1)车辆的载重量和所需车辆的数量成 比例。
(2)如果用载重量为4.8吨的卡车来运,一共需要多少辆卡车?(用比例解)
18.(2022·河北石家庄·统考小升初真题)一个圆柱,在直径位置沿高切开分成完全相同的两部分,两部分的表面积之和比圆柱的表面积增加了40平方分米。这个圆柱的体积是多少?
19.(2022·河南开封·统考小升初真题)为了丰富学生的课余生活,学校对六年级参加绘画、书法、舞蹈、乐器这四个社团中的人员分布情况进行抽样调查。并根据收集的数据绘制了如图两幅不完整的统计图。请根据如图提供的信息解答下面的问题。
(1)此次一共调查了多少名学生?
(2)将条形统计图补充完整。
(3)从统计图中你有什么发现?
20.(2022·陕西汉中·统考小升初真题)为保障疫情期间的医疗物资供应,全国各地医疗物资生产企业加班加点生产,某企业接到生产一批防护服的任务,第一天生产的套数与总套数的比是1∶5,第二天生产了660套防护服,两天完成的套数比未完成的套数少。这批防护服的生产任务共是多少套?
21.(2022·山东菏泽·统考小升初真题)一个圆锥的底面半径是3分米。从圆锥的顶点沿着高将它切成相等的两半后,表面积比原来的圆锥表面积增加了24平方分米。这个圆锥的体积是多少立方分米?
22.(2022·山东菏泽·统考小升初真题)一个圆柱形水池,直径10米,深1米。
(1)在池底及池壁抹一层水泥,抹水泥的面积是多少?
(2)这个水池能装水多少立方米?
23.(2022·山东菏泽·统考小升初真题)下面每格代表5m,小兔的起始位置在0点处。
(1)小兔先向西跳了4格到A点。在图上标出A点。
(2)小兔再从A点向东跳了30m到了B点,在图上标出B点。
(3)A点和B点离0点的距离分别是( )米和( )米。
24.(2022·内蒙古通辽·统考小升初真题)长方体的高是5厘米,上底、下底是边长4厘米的正方形,把它削成最大的圆柱。计算出圆柱的体积。
25.(2022·山西晋中·统考小升初真题)成语“立竿见影”在《辞源》里的解释为“竿立而影现,喻收效迅速。”用数学的眼光来看,这是应用了比例知识中的( )关系。(填“正比例”或“反比例”)
希望小学开展了测量旗杆有多高的实践活动。同学们进行了如下操作:某天下午5时,先测出旗杆的影子长度,接着在同一时间,同一地点,测得两棵树的高度和它们影子的长度,如图所示:
旗杆的高度是多少?请用所学数学知识解释说明。
26.(2022·山西晋中·统考小升初真题)沙漏又称沙钟,是我国古代一种计量时间的仪器。(如图)上下是两个完全相同的圆锥形容器,其中一个装满细沙,利用细沙的流动性和重力作用,根据流沙从一个容器漏到另一个容器的数量来计算时间。
(1)如果沙漏上部的圆锥装满细沙,求沙子的体积。
(2)如果漏口每分钟漏出细沙31.4立方厘米,漏完全部沙子需要几分钟?
27.(2022·河南商丘·统考小升初真题)每年的6月5日是世界环境日,它的设立表达了人类对美好环境的向往和追求。笑笑家为了节约用水,做了一个无盖圆柱形铁皮水桶蓄水,高10分米,底面直径是高的,做这个水桶至少要用多少平方分米的铁皮?
28.(2022·河南省直辖县级单位·统考小升初真题)小敏的妈妈想在网上购买一件衣服,两个网店的标价都是320元,但是A店打出七五折优惠,B店打出每满100元减25元的优惠。请告诉小敏的妈妈,到哪个网店购买更省钱?
29.(2022·河南鹤壁·统考小升初真题)在炎热的夏天到来之际,张叔叔准备建一个标准化的长方体游泳池,这个游泳池的长是50m,宽是长的一半,深1.8m。
(1)建成这个游泳池共需挖土多少立方米?
(2)在池的侧面和池底抹一层水泥,抹水泥的面积是多少平方米?
30.(2022·山东临沂·统考小升初真题)华苑小学对全校学生进行了体重调查,体重正常的学生有319人。如图是调查结果统计图。
(1)华苑小学共有学生多少人?
(2)体重偏重、偏轻的学生各有多少人?
(3)分析以上数据,你有什么建议?
31.(2022·甘肃平凉·统考小升初真题)如图,三角形ABC是直角三角形,圆的直径是4厘米,阴影甲-阴影乙=2.5平方厘米,则三角形中BC边长是多少厘米?(π取值为3)
32.(2022·内蒙古通辽·统考小升初真题)工艺品厂要制作6000个中国结,前3天制作完成了总工作量的20%。照这样计算,还需要多少天全部制作完成?
33.(2022·内蒙古通辽·统考小升初真题)一个圆锥形沙堆,底面积是平方米,高是1.8米。把这堆沙铺在宽为5米,长为12米的路面上,厚度大约是多少厘米?(保留整厘米)
34.(2022·内蒙古通辽·统考小升初真题)一个长方形菜地的周长是160米,长比宽的2倍多8米,这块菜地的面积是多少平方米?
35.(2022·内蒙古通辽·统考小升初真题)李师傅要加工一批零件。他第一天完成了总数量的,第二天加工了200个,这两天共完成了总数的60%。这批零件一共有多少个?
36.(2022·内蒙古通辽·统考小升初真题)在一幅比例尺是1∶1000000的地图上,甲、乙两座城市相距5.2厘米。一辆轿车和一辆客车分别从甲城和乙城同时相向而行,轿车每小时行驶70千米,客车每小时行驶60千米。经过多长时间两车相遇?
37.(2022·内蒙古呼伦贝尔·统考小升初真题)这只工具箱的表面积是多少?(单位:分米)
38.(2022·内蒙古呼伦贝尔·统考小升初真题)根据下面的路线图,用自己的语言说说从学校到体育馆的路线。
39.(2022·广西百色·统考小升初真题)一根长2米,横截面直径是20厘米的木头浮在水面上,它正好是一半露出水面。
(1)这根木头的体积是多少立方厘米?
(2)这根木头与水接触的面积是多少平方厘米?
40.(2022·辽宁沈阳·统考小升初真题)体育用品商店。
(1)打折后,每个足球是多少元?
(2)笑笑和奇思共买了2个篮球、2副羽毛球拍和6个羽毛球,比打折前便宜多少元?
参考答案:
1.(1)16,24
(2)80名
(3)见详解
(4)见详解
【分析】(1)通过观察条形统计图可知,成绩及格的有16人,优秀的有24人;
(2)把抽测的人数看作单位“1”,其中及格的有16人,占抽测人数的20%,根据已知一个数的百分之几是多少,求这个数,用除法求出抽测的人数;
(3)再根据求一个数的百分之几是多少,用乘法求出不及格的人数,再根据减法的意义,用减法求出成绩良好的人数,据此补充条形统计图;
(4)根据求一个数是另一个数的百分之几,用除法求出优秀的占抽测人数的百分之几,用减法求出成绩良好的占抽测人数的百分之几,据此完成扇形统计图。
【详解】(1)成绩及格的有16人,优秀的有24人。
(2)16÷20%
=16÷0.2
=80(人)
答:六年级有80名学生参加了体能测试。
(3)80×5%=4(人)
80-(4+16+24)
=80-44
=36(人)
作图如下:
(4)优秀的占总人数的:
24÷80×100%
=0.3×100%
=30%
良好的占总人数的:
1-5%-20%-30%=45%
作图如下:
【点睛】此题考查的目的是理解掌握条形统计图、扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
2.220元
【分析】根据题意,八折就是80%,把衣服原价看作单位“1”,优惠了(1-80%),用500×(1-80%),求出优惠的钱数,500元大于360元,说明这件衣服优惠了120元,再加上打八折优惠的钱数,即可求出这件衣服优惠的钱数。
【详解】500×(1-80%)+120
=500×20%+120
=100+120
=220(元)
答:一共可以优惠220元。
【点睛】本题考查折扣问题,打几折就是百分之几十。
3.376.8平方厘米;653.12立方厘米
【分析】根据题意,求至少需要用多少彩纸,就是求这个圆柱形笔筒的表面积去掉一个底面的面积,根据圆柱的表面积公式:侧面积+底面积,代入数据,求出需要的彩纸的面积;再根据圆柱的体积公式:底面积×高,代入数据,即可解答。
【详解】3.14×(8÷2)2+3.14×8×13
=3.14×16+25.12×13
=50.24+326.56
=376.8(平方厘米)
3.14×(8÷2)2×13
=3.14×16×13
=50.24×13
=653.12(立方厘米)
答:至少需要用376.8平方厘米的彩纸,这个笔筒的体积是653.12立方厘米。
【点睛】利用圆柱的表面积公式、体积公式进行解答,关键是熟记公式。
4.52500元
【分析】根据利息=本金×利率×时间,代入数据,求出利息,再加上本金,即可解答。
【详解】五万=50000元
50000×2.50%×2+50000
=1250×2+50000
=2500+50000
=52500(元)
答:到期时可以取回52500元。
【点睛】本题考查利率问题,关键是熟记利息公式。
5.135.02平方米
【分析】求贴瓷砖的面积就是求圆柱的一个底面积和一个侧面积的和,利用S表=πr2+2πrh计算解答。
【详解】3.14×10×1.8+3.14×(10÷2)2
=31.4×1.8+3.14×25
=56.52+78.5
=135.02(平方米)
答:这个水池贴瓷砖的面积是135.02平方米。
【点睛】此题主要考查圆柱体的表面积,解答时一定要注意分清题目中的条件,灵活解答。
6.20千克
【分析】先把甲袋大米的质量看作单位“1”,取出后,再剩下(1-),根据分数乘法的意义,即可求出此时甲袋所剩大米的质量。再把甲袋所剩大米的质量平均分成8份,先用除法求出1份的质量,再用乘法求出3份的质量,即乙袋取出25%后剩大米的质量。再把乙袋原来大米的质量看作单位“1”,根据百分数除法的意义,用乙袋所剩大米的质量除以(1-25%),就是乙袋大米原来的质量。
【详解】60×(1-)÷8×3÷(1-25%)
=60×÷8×3÷75%
=20(千克)
答:乙袋中原来有20千克大米。
【点睛】关键是根据分数乘法的意义,求出甲袋取出后剩下的质量。除按上述解答方法外,也可把比转化成分数,求出乙袋取出25%后剩的质量,然后再根据百分数除法的意义,求乙袋原来的质量。
7.(1)(2)见详解;
(3)1∶4
【分析】(1)O点位置不变,确定出三角形另外两个顶点的位置,顺次连线。
(2)将图形②的底和高同时扩大到原来的2倍,画出扩大后的图形。
(3)分别求出图①与图③的面积,再写出它们的面积比。
【详解】(1)(2)如图:
(3)4×2÷2=4;
4×8÷2=16;
图①与图③的面积比是4∶16=1∶4。
【点睛】本题考查了图形的旋转、图形的放大与缩小,关键是能准确画图。
8.1470000平方米
【分析】把总面积看成单位“1”,用减法计算得出粮食作物种植面积占的百分率,总面积的20%对应的数量是42公顷,由此用除法求出总面积,再乘粮食作物种植面积占的百分率,即可得粮食作物种了多少平方米。
【详解】1-20%-10%=70%
42÷20%×70%
=210×70%
=147(公顷)
147公顷=1470000平方米
答:粮食作物种了1470000平方米。
【点睛】本题主要考查了扇形统计图,已知一个数的百分之几是多少,求这个数,用除法计算;已知一个数,求它的百分之几是多少,用乘法计算。
9.(1)0(2)右;左(3)4;﹣4(4)向西走5米;2米;图见详解
【分析】(1)0是正数和负数的分界点;据此解答;
(2)根据正负数在数轴上的位置,结合题干,直接填空即可;
(3)根据数轴上到原点的距离相等的数有两个,这两个数互为相反数的特点进行解答即可;
(4)用正负数表示意义相反的两种量:向东走记作正,则向西走就记作负,由此得解。
【详解】(1)0是正数和负数的分界点。
(2)所有的正数都在0的右边,所有的负数都在0的左边。
(3)在直线上,距0点4个单位长度的点分别是4和﹣4。
(4)这个人走﹣5米到B点表示向西走5米。
5-3=2(米)
这时他距离出发点有2米。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
10.30元
【分析】用故事书的标价5.4元乘5,再加上3元,求出这本字典的标价。
【详解】5.4×5+3
=27+3
=30(元)
答:这本字典标价30元。
【点睛】本题考查了小数乘法应用题,求一个数的几倍是多少,用这个数乘倍数。
11.(1)图见详解,(2,7);(2)(3)见详解
【分析】(1)圆心确定圆的位置,半径确定圆的大小,由此先将点A向上平移5格,再以平移后的点A为圆心,以2为半径即可画出这个平移后的图形,再利用数对表示位置的方法表示平移后A点的位置;
(2)用三角板的一条直角边的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和B点重合,过B沿直角边向已知直线a画直线即可;
(3)明确旋转中心以P点为旋转中心,确定旋转方向和角度,顺时针旋转90°,先描出旋转后的对应点再连线即可。
【详解】(1)画出将圆A向上平移5格后的图形①,平移后A点的位置用数对表示是(2,7)。
(1)(2)(3)作图如下:
【点睛】本题考查了图形的平移、旋转及垂线的画法,关键是画图要准确。
12.40%;6人
【分析】把该班总人数看作单位“1”,用减法计算即可得O型血的人数占全班人数的百分之几;用该班的总人数分别乘O型血的人数和A型血的人数占总人数的百分率,再相减即可。
【详解】1-24%-28%-8%
=76%-28%-8%
=40%
50×40%-50×28%
=20-14
=6(人)
答:O型血的人数占全班人数的40%,O型血的人数比A型血的人数多6人。
【点睛】此题主要考查的是如何从扇形统计图中获取信息,然后再根据信息进行计算的能力。
13.3202.8千克
【分析】观察图形可知,粮仓是一个底面直径是2米,高是1.5米的圆柱体和底面直径是2米,高是0.6米的圆锥体;根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×,代入数据,求出这个粮仓的体积,再乘600,即可解答,
【详解】3.14×(2÷2)2×1.5+3.14×(2÷2)2×0.6×
=3.14×1×1.5+3.14×1×0.6×
=3.14×1.5+3.14×0.6×
=4.71+1.884×
=4.71+0.628
=5.338(立方米)
5.338×600=3202.8(千克)
答:这个粮仓最多能装3202.8千克粮食。
【点睛】利用圆柱的体积公式、圆锥的体积公式进行解答,关键是熟记公式。
14.395.64毫升
【分析】根据图示可知,瓶子的容积包括高8厘米水的体积和高6厘米空白部分圆柱的体积,据此计算这两部分的体积和即可。
【详解】3.14×(6÷2)2×(8+6)
=3.14×9×14
=395.64(立方厘米)
395.64立方厘米=395.64毫升
答:这个饮料瓶的容积是395.64毫升。
【点睛】此题主要考查了圆柱体的体积公式的意义,及在生活中的实际应用。
15.(1)40;(2)8;(3)见详解
【分析】(1)把总人数看作单位“1”,其中自驾去参展的有20人,占总人数的50%,根据已知一个数的百分之几是多少,求这个数,用除法解答;(2)步行前往的占20%,根据求一个数的百分之几是多少,用乘法解答;(3)根据步行的人数,完成条形统计图。
【详解】(1)20÷50%=40(名)
(2)40×20%=8(名)
(3)条形统计图补充如下:
【点睛】本题主要考查的是理解掌握扇形统计图、条形统计图的特点及作用,解答本题的关键是根据统计图提供的信息,解决有关的实际问题。
16.1000元
【分析】医疗费-起付金额=报销部分,将报销部分看作单位“1”,报销部分×报销百分比=报销金额,医疗费-报销金额=自付金额,据此列式解答。
【详解】2800-(2800-400)×75%
=2800-2400×0.75
=2800-1800
=1000(元)
答:按规定王大伯自付1000元。
【点睛】关键是确定单位“1”,整体数量×部分对应百分率=部分数量。
17.(1)反
(2)25辆
【分析】(1)2.5×48=4×30=5×24=120,得出:车辆的载重量×所需车辆的数量=总重量,则车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例。
(2)设一共需要x辆卡车。因为车辆的载重量×所需车辆的数量=总重量(一定),所以4.8乘x的积等于2.5×48的积,据此即可解答。
【详解】(1)因为2.5×48=120(吨),4×30=120(吨),车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例。
(2)解:设一共需要x辆卡车。
4.8x=2.5×48
4.8x÷4.8=2.5×48÷4.8
x=25
答:一共需要25辆。
【点睛】本题考查了学生正反比例的判断情况,能运用统计表提供的信息解决问题。同时考查了学生理解分析问题的能力。
18.62.8立方分米
【分析】通过观察图形可知,把圆柱纵切成两半,表面积增加的是两个截面的面积,每个截面的长等于圆柱的高,每个截面的宽等于圆柱的底面直径,据此可以求出圆柱的底面直径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【详解】40÷2÷5
=20÷5
=4(分米)
3.14×(4÷2)2×5
=3.14×4×5
=12.56×5
=62.8(立方分米)
答:这个圆柱的体积是62.8立方分米。
【点睛】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式,重点是求出圆柱的底面直径。
19.(1)200名
(2)见详解
(3)我发现了参加书法的人数占了总人数的10%,参加舞蹈的人数占总人数的15%,参加绘画的人数最多,参加书法的人数最少。(答案不唯一)
【分析】(1)根据图中的信息可知,绘画的人数是90人,占了总人数的45%,用绘画的人数除以绘画所占总人数的百分比即可;
(2)求出参加乐器的人数,再根据画条形统计图的方法,把图补充完整即可;
(3)根据图中所给的信息,分析数据写出的发现合理即可。
【详解】(1)90÷45%=200(名)
答:此次一共调查了200名学生。
(2)200-90-20-30
=110-20-30
=90-30
=60(人)
(3)我发现了参加书法的人数占了总人数的10%,参加舞蹈的人数占总人数的15%,参加绘画的人数最多,参加书法的人数最少。(答案不唯一)。
【点睛】此题考查了学生分析数据的能力和运算能力,考查了条形统计图、扇形统计图等知识。
20.2700套
【分析】设这批防护服的生产任务一共是x套,第一天生产的套数与总套数的比是1∶5,第一天生产x(套),根据等量关系:两天完成的套数=未完成的套数×(1-),列方程解答即可。
【详解】解:设这批防护服的生产任务一共是x套。
x+660=(x-x-660)×(1-)
x+660=(x-660)×
x+660=x-528
x=1188
x=2700
答:这批防护服的生产任务一共是2700套。
【点睛】本题主要考查了比及分数的应用,关键是根据等量关系:两天完成的套数=未完成的套数×(1-),列方程。
21.37.68立方分米
【分析】通过观察图形可知,把这个圆锥纵向切开,表面积增加的是两个切面的面积,每个切面的底等于圆锥的底面直径,每个切面的高等于圆锥的高,根据三角形的面积公式:S=ah÷2,那么h=2S÷a,据此求出圆锥的高,再根据圆锥的体积公式:V=,把数据代入公式解答。
【详解】24÷2=12(平方分米)
12×2÷(3×2)
=24÷6
=4(分米)
×3.14×32×4
=×3.14×9×4
=37.68(立方分米)
答:这个圆锥的体积是37.68立方分米。
【点睛】此题主要考查三角形的面积公式、圆锥的体积公式的灵活运用,关键是熟记公式,重点是求出圆锥的高。
22.(1)109.9平方米
(2)78.5立方米
【分析】(1)抹水泥的面是圆柱的底面和侧面,所以利用公式求出它的底面积和侧面积,再相加求出抹水泥的面积即可;
(2)根据圆柱的体积公式,代入数据求出这个水池能装水多少立方米。
【详解】(1)3.14×10×1+3.14×(10÷2)2
=3.14×10+3.14×25
=3.14×35
=109.9(平方米)
答:抹水泥的面积是109.9平方米。
(2)3.14×(10÷2)2×1
=3.14×25×1
=78.5(立方米)
答:这个水池能装水78.5立方米。
【点睛】本题考查了圆柱的表面积和体积,无盖圆柱表面积=底面积+侧面积,圆柱体积=底面积×高。
23.(1)见详解
(2)见详解
(3)20;10
【分析】根据数轴知识,分别标出A和B的位置即可,然后根据A和B距离0点的距离解答。
【详解】(1)
(2)30÷5=6(格)
6-4=2(格)
(3)A点离0点的距离分别是:
5×4=20(m)
B点离0点的距离分别是:
5×2=10(m)
【点睛】本题考查了数轴知识,结合题意解答即可。
24.62.8cm3
【分析】由题意分析可知,圆柱的底面直径是长方体底面的边长,即4厘米,高等于长方体的高,然后根据圆柱的体积公式进行计算即可。
【详解】3.14×(4÷2)2×5
=3.14×4×5
=62.8(立方厘米)
答:圆柱的体积是62.8立方厘米。
【点睛】本题主要考查长方体和圆柱的关系以及圆柱的体积公式。
25.正比例;15米
【分析】因为:影长÷杆长=每米杆子的影长(一定),所以影长和杆长成正比例。物体的长度和它的影子的长度的比值一定,即物体的长度和它的影子的长度的成正比例,由此列式解答即可。
【详解】“竿立而影现,喻收效迅速。”用数学的眼光来看,这是应用了比例知识中的正比例关系。
解:设旗杆的高度是x米,
x∶20=3∶4
4x=60
x=15
答:旗杆的高度是15米。
【点睛】解答此题的关键是,先判断题中的两种相关联的量成何比例,然后找准对应量,列式解答即可。
26.(1)157立方厘米
(2)5分钟
【分析】(1)由图形可以得到沙漏上部沙子的底面直径为10厘米,高为6厘米,如此利用圆锥的体积公式即可求出答案;
(2)根据上部沙漏沙子的体积可得其速度,再结合下部沙子的体积用除法求解即可。
【详解】(1)3.14×(10÷2)2×6×
=3.14×25×6×
=78.5×6×
=471×
=157(立方厘米)
答:沙漏上部沙子的体积是157立方厘米。
(2)157÷31.4=5(分钟)
答:漏完全部沙子需要5分钟。
【点睛】这是一道关于圆锥应用的题目,关键是掌握圆锥的体积公式。
27.138.6平方分米
【分析】因为底面直径是高的,高是8分米,所以底面直径为:10×=4(分米)。因为是无盖水桶,所以它的表面积等于圆柱的侧面积加上底面积即可。
【详解】10×=4(分米)
3.14×4×10+3.14×(4÷2)2
=125.6+12.56
=138.16(平方分米)
答:这个水桶至少要用铁皮138.6平方分米。
【点睛】本题的解答关键在于先求出底面直径,再根据圆柱的表面积公式即可解答。
28.A网店
【分析】A店打出七五折优惠,就是售价是原价的75%,用原价乘75%即可;B店打出每满100元减25元的优惠,320÷100=3(个)……20(元),320元里面最多有3个100元,可以减去3个25元;分别求出两个网店需要的钱数,然后再比较解答。
【详解】A店:320×75%=240(元);
B店:320÷100=3(个)……20(元);
320-25×3
=320-75
=245(元);
240<245;
答:到A网店购买更省钱。
【点睛】解答此题的关键是根据两个网店的促销活动,计算出每个网店需要花的钱数,然后再进行比较即可。
29.(1)2250立方米;(2)1520平方米
【分析】(1)需要挖土的体积就是这个游泳池的体积,用长方体的体积公式V=abh,解答即可。
(2)抹水泥的面积是长方体5个面的面积,缺少上面,则抹水泥的面积=长×宽+长×高×2+宽×高×2,据此解答。
【详解】(1)50÷2=25(米)
50×25×1.8=2250(立方米)
答:建这个游泳池共需挖土2250立方米。
(2)50×25+50×1.8×2+25×1.8×2
=1250+180+90
=1520(平方米)
答:抹水泥的面积是1520平方米。
【点睛】解答有关长方体表面积和体积的实际问题,一定要搞清所求的是什么,再进一步选择合理的计算方法解答问题。要熟练掌握并灵活运用长方体的表面积和体积公式。
30.(1)580人
(2)偏重:203人,偏轻:58人
(3)见详解
【分析】(1)把全校学生人数看作单位“1”,体重正常的学生有319人,占55%,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(2)根据求一个数的百分之几是多少,用乘法解答。
(3)根据统计图给出合理建议即可。(答案不唯一)
【详解】(1)319÷55%=580(人)
答:华苑小学共有学生580人。
(2)580×35%=203(人)
580×10%=58(人)
答:体重偏重的学生有203人,偏轻的学生有58人。
(3)建议体重偏重的同学,加强体育锻炼,少吃脂肪含量高的食物,建议体重偏轻的同学,不要挑食偏食,合理搭配食物,健康成长。(答案不唯一)
【点睛】此题考查的目的是理解掌握扇条统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
31.4.75厘米
【分析】阴影甲的面积=半圆的面积-空白部分的面积,阴影乙的面积=三角形ABC的面积-空白部分的面积,再根据阴影甲-阴影乙=2.5平方厘米,所以半圆的面积-空白部分的面积-(三角形ABC的面积-空白部分的面积)=2.5平方厘米,即半圆的面积-三角形ABC的面积=2.5平方厘米,利用圆和三角形的面积公式,代入数据求解即可。
【详解】3×(4÷2)2-4×BC÷2=2.5
3×4-2BC=2.5
12-2BC=2.5
2BC=12-2.5
2BC=9.5
BC=4.75
答:三角形中BC边长是4.75厘米。
【点睛】本题主要考查了组合图形的面积,解题的关键是把不规则图形转化为规则图形。
32.12天
【分析】3天就完成了20%,根据分数除法的意义,完成这些任务共需要(3÷20%)天,再减3天,即可得还需要多少天全部制作完成。
【详解】3÷20%-3
=15-3
=12(天)
答:还需要12天全部制作完成。
【点睛】本题主要考查了百分数的实际应用,已知一个数的百分之几是多少,求这个数,用除法计算。
33.16厘米
【分析】根据圆锥体积=底面积×高÷3,求出沙堆体积,再根据长方体的高=体积÷底面积,求出沙子厚度即可。
【详解】15.8×1.8÷3=9.48(立方米)
9.48÷(12×5)
=9.48÷60
=0.158(米)
≈16(厘米)
答:厚度大约是16厘米。
【点睛】关键是掌握并灵活运用长方体和圆锥体积公式。
34.1344平方米
【分析】用160÷2=80求出一组长与宽的和,再根据和倍问题用(80-8)÷(2+1)即可求出宽的长度,进而求出长。最后根据“长方形面积=长×宽”求出面积即可。
【详解】(160÷2-8)÷(2+1)
=72÷3
=24(米)
24×2+8
=48+8
=56(米)
56×24=1344(平方米)
答:这块菜地的面积是1344平方米。
【点睛】解答本题的关键是根据和倍问题先求出长和宽分别是多少,再进一步求出面积。
35.500个
【分析】将零件总数看作单位“1”,两天共完成的对应百分率-第一天完成的对应分率=第二天完成的对应分率或百分率,第二天完成数量÷对应分率或百分率=零件总数,据此列式解答。
【详解】200÷(60%-)
=200÷0.4
=500(个)
答:这批零件一共有500个。
【点睛】关键是确定单位“1”,部分数量÷对应分率或百分率=整体数量。
36.0.4小时
【分析】根据“实际距离=图上距离÷比例尺”解得甲乙两地的距离,然后根据“相遇时间=路程和÷速度和”求出两车的相遇时间。
【详解】1∶1000000=
5.2÷=5200000(厘米)
5200000厘米=52千米
52÷(70+60)
=52÷130
=0.4(小时)
答:经过0.4小时后两车相遇。
【点睛】本题主要考查的是实际距离和图上距离的转化,以及行程问题中的相遇问题,相遇时间=路程和÷速度和。
37.117.96平方分米
【分析】通过观察图形可知,上面的半圆柱求出一个底面的面积加上圆柱侧面积的一半,下面的长方体求它的5个面的面积,根据圆的面积公式:S=πr2,圆柱的侧面积公式:S=πdh,长方形的面积公式:S=a×b,把数据分别代入公式解答。
【详解】3.14×22+3.14×2×2×5÷2+5×4+5×3×2+4×3×2
=3.14×4+12.56×5÷2+20+30+24
=12.56+31.4+20+30+24
=63.96+30+24
=117.96(平方分米)
答:它的表面积是117.96平方分米。
【点睛】此题主要考查圆柱的表面积公式、长方体的表面积公式的灵活运用,关键是熟记公式。
38.学校到体育馆的路线:从学校向东走200米到文化宫,再向北偏东45°方向走400米到体育馆。
【详解】依据地图上的方向辨别方法,即“上北下南,左西右东”,即可描述出从学校到体育馆的路线。
【解答】
测出文化宫与体育馆之间的夹角是45°
测量出学校到文化宫图上距离2厘米,实际距离:
2÷=20000(厘米)
20000厘米=200米
测量出文化宫到体育馆图上距离4厘米,实际距离:
4÷=40000(厘米)
40000厘米=400米
所以学校到体育馆的路线:
从学校向东走200米到文化宫,再向北偏东45°方向走400米到体育馆。
【点睛】此题主要考查依据方向(角度)和距离判定物体位置的方法,首先要根据比例尺计算出实际距离,再根据图示说出路线。
39.(1)62800立方厘米;
(2)6594平方厘米
【分析】先计算出圆柱体木头的半径是多少,再把长2米转化为以厘米为单位的数。
(1)根据圆柱的体积=底面积×高进行计算即可得到答案;
(2)这根木头与水接触的面积就是这根圆柱体木头表面积的一半,可根据圆柱的表面积公式进行计算即可得到答案。
【详解】木头横截面的半径为:20÷2=10(厘米)
2米=200厘米
(1)3.14×102×200
=314×200
=62800(立方厘米)
答:这根木头的体积约是62800立方厘米。
(2)两个底面积:
3.14×102×2
=314×2
=628(平方厘米)
侧面积:
3.14×20×200
=62.8×200
=12560(平方厘米)
表面积:628+12560=13188(平方厘米)
与水接触的面积:13188÷2=6594(平方厘米)
答:这根木头与水接触的面积是6594平方厘米。
【点睛】充分结合示意图,展开空间思维,想象出木头与水接触的面的具体特征,是解题关键。
40.(1)57.6元
(2)58元
【分析】八折是指现价是原价的80%;
(1)把足球的原价看成单位“1”,用原价乘上80%就是打折后的单价;
(2)先求出2个篮球、2副羽毛球拍和6个羽毛球的价钱,然后把原价看成单位“1”,用原价乘上(1-80%)就是便宜的钱数。
【详解】(1)72×80%=57.6(元)
答:每个足球是57.6元。
(2)(96×2+40×2+3×6)×(1-80%)
=(192+80+18)×20%
=290×20%
=58(元)
答:比打折前便宜了58元。
【点睛】解决本题关键是理解打折的含义,再找出单位“1”,根据分数乘法的意义求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初真题分类特训:解决问题(专项训练)-小学数学六年级下册北师大版
1.(2022·湖南株洲·统考小升初真题)弘毅小学从六年级任意抽取若干名学生进行体能测试,并根据收集的数据绘制成如图两幅统计图。请结合这两幅统计图提供的信息,回答下面的问题。
(1)成绩及格的有 名,优秀的有 名。
(2)六年级有多少学生参加了体能测试?
(3)请把条形统计图补充完整。
(4)请把扇形统计图缺少的信息填写完整。
2.(2022·河北唐山·统考小升初真题)今年六月份,唐山市政府助商惠民发放1.5亿消费补贴券,张阿姨领到了一张商超类消费券满360元减120元。商场正在搞八折促销活动,她买一件500元的衣服,一共可以优惠多少元?
3.(2022·河北唐山·统考小升初真题)小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸?这个笔筒的体积是多少?
4.(2022·河北唐山·统考小升初真题)妈妈把五万元钱存入银行,存期为2年,年利率为2.50%。到期时可以取回多少钱?
5.(2022·广东阳江·统考小升初真题)有一个底面直径10米,高1.8米圆柱形水池,如果在水池内壁和底面都要贴上瓷砖,这个水池贴瓷砖的面积是多少平方米?
6.(2022·广东阳江·统考小升初真题)有甲、乙两袋大米,甲袋有60千克,从甲袋取出,从乙袋取出25%后,甲、乙两袋剩余大米的质量比是8∶3。乙袋中原来有多少千克大米?
7.(2022·重庆忠县·统考小升初真题)在如图所示按要求作图。
(1)画出图①绕点O顺时针旋转90°的图,得到图②。
(2)按2∶1的比例画出图②放大后的图,得到图③。
(3)图①与图③的面积比是( )。
8.(2022·重庆忠县·统考小升初真题)宝山村2021年农作物种植面积如图所示,其中棉花种了42公顷。粮食作物种了多少平方米?
9.(2022·山东菏泽·统考小升初真题)看图填空。
(1)( )是正数和负数的分界点。
(2)所有的正数都在0的( )边,所有的负数都在0的( )边。
(3)在直线上,距0点4个单位长度的点分别是( )和( )。
(4)如果一个人从0点先向东走3米记作﹢3米到A点,那么这个人又走﹣5米到B点是什么意思?这时他距离出发点有多远?在直线上表示出来。
10.(2022·青海海南·统考小升初真题)一本字典的标价比一本故事书标价的5倍多3元。这本故事书标价5.4元,这本字典标价多少元?
11.(2022·吉林白山·统考小升初真题)
(1)画出将圆A向上平移5格后的图形,平移后A点的位置用数对表示是( )。
(2)过B点作直线a的垂线。
(3)画出把三角形EPF绕P点顺时针旋转90°后的图形。
12.(2022·吉林白山·统考小升初真题)六(2)班同学血型情况加图。该班有50人,O型血的人数占全班人数的百分之几?比A型血的人数多多少人?
13.(2022·安徽阜阳·统考小升初真题)一个粮仓如图,如果每立方米粮食的质量为600千克,这个粮仓最多能装多少千克粮食?
14.(2022·辽宁鞍山·统考小升初真题)如图,一个内直径是6厘米的饮料瓶内饮料的高度是8厘米,将这个饮料瓶的瓶盖拧紧倒置放平,空余部分的高度是6厘米。这个饮料瓶的容积是多少毫升?
15.(2022·辽宁鞍山·统考小升初真题)学校组织老师去博物馆参展,前往博物馆,自驾车,乘公交车和步行的人数如条形统计图(部分)和扇形统计图所示。
(1)学校共有( )名老师去参展。
(2)步行前往博物馆的有( )名老师。
(3)把条形统计图补充完整。
16.(2022·福建泉州·统考小升初真题)王大伯参加了某县农村合作医疗保险。条款规定:起付400元,余下的按75%报销。今年王大伯患急性肠炎在县人民医院住院治疗9天,共计医疗费2800元。按规定王大伯自付多少元?
17.(2022·四川广安·统考小升初真题)物流公司要将一批货物运往加工厂,如果要一次把这批货物全部运出,车辆的载重量与所需车辆的数量如下表。
载重量(吨) 2.5 3 5
数量(辆) 48 40 24
(1)车辆的载重量和所需车辆的数量成 比例。
(2)如果用载重量为4.8吨的卡车来运,一共需要多少辆卡车?(用比例解)
18.(2022·河北石家庄·统考小升初真题)一个圆柱,在直径位置沿高切开分成完全相同的两部分,两部分的表面积之和比圆柱的表面积增加了40平方分米。这个圆柱的体积是多少?
19.(2022·河南开封·统考小升初真题)为了丰富学生的课余生活,学校对六年级参加绘画、书法、舞蹈、乐器这四个社团中的人员分布情况进行抽样调查。并根据收集的数据绘制了如图两幅不完整的统计图。请根据如图提供的信息解答下面的问题。
(1)此次一共调查了多少名学生?
(2)将条形统计图补充完整。
(3)从统计图中你有什么发现?
20.(2022·陕西汉中·统考小升初真题)为保障疫情期间的医疗物资供应,全国各地医疗物资生产企业加班加点生产,某企业接到生产一批防护服的任务,第一天生产的套数与总套数的比是1∶5,第二天生产了660套防护服,两天完成的套数比未完成的套数少。这批防护服的生产任务共是多少套?
21.(2022·山东菏泽·统考小升初真题)一个圆锥的底面半径是3分米。从圆锥的顶点沿着高将它切成相等的两半后,表面积比原来的圆锥表面积增加了24平方分米。这个圆锥的体积是多少立方分米?
22.(2022·山东菏泽·统考小升初真题)一个圆柱形水池,直径10米,深1米。
(1)在池底及池壁抹一层水泥,抹水泥的面积是多少?
(2)这个水池能装水多少立方米?
23.(2022·山东菏泽·统考小升初真题)下面每格代表5m,小兔的起始位置在0点处。
(1)小兔先向西跳了4格到A点。在图上标出A点。
(2)小兔再从A点向东跳了30m到了B点,在图上标出B点。
(3)A点和B点离0点的距离分别是( )米和( )米。
24.(2022·内蒙古通辽·统考小升初真题)长方体的高是5厘米,上底、下底是边长4厘米的正方形,把它削成最大的圆柱。计算出圆柱的体积。
25.(2022·山西晋中·统考小升初真题)成语“立竿见影”在《辞源》里的解释为“竿立而影现,喻收效迅速。”用数学的眼光来看,这是应用了比例知识中的( )关系。(填“正比例”或“反比例”)
希望小学开展了测量旗杆有多高的实践活动。同学们进行了如下操作:某天下午5时,先测出旗杆的影子长度,接着在同一时间,同一地点,测得两棵树的高度和它们影子的长度,如图所示:
旗杆的高度是多少?请用所学数学知识解释说明。
26.(2022·山西晋中·统考小升初真题)沙漏又称沙钟,是我国古代一种计量时间的仪器。(如图)上下是两个完全相同的圆锥形容器,其中一个装满细沙,利用细沙的流动性和重力作用,根据流沙从一个容器漏到另一个容器的数量来计算时间。
(1)如果沙漏上部的圆锥装满细沙,求沙子的体积。
(2)如果漏口每分钟漏出细沙31.4立方厘米,漏完全部沙子需要几分钟?
27.(2022·河南商丘·统考小升初真题)每年的6月5日是世界环境日,它的设立表达了人类对美好环境的向往和追求。笑笑家为了节约用水,做了一个无盖圆柱形铁皮水桶蓄水,高10分米,底面直径是高的,做这个水桶至少要用多少平方分米的铁皮?
28.(2022·河南省直辖县级单位·统考小升初真题)小敏的妈妈想在网上购买一件衣服,两个网店的标价都是320元,但是A店打出七五折优惠,B店打出每满100元减25元的优惠。请告诉小敏的妈妈,到哪个网店购买更省钱?
29.(2022·河南鹤壁·统考小升初真题)在炎热的夏天到来之际,张叔叔准备建一个标准化的长方体游泳池,这个游泳池的长是50m,宽是长的一半,深1.8m。
(1)建成这个游泳池共需挖土多少立方米?
(2)在池的侧面和池底抹一层水泥,抹水泥的面积是多少平方米?
30.(2022·山东临沂·统考小升初真题)华苑小学对全校学生进行了体重调查,体重正常的学生有319人。如图是调查结果统计图。
(1)华苑小学共有学生多少人?
(2)体重偏重、偏轻的学生各有多少人?
(3)分析以上数据,你有什么建议?
31.(2022·甘肃平凉·统考小升初真题)如图,三角形ABC是直角三角形,圆的直径是4厘米,阴影甲-阴影乙=2.5平方厘米,则三角形中BC边长是多少厘米?(π取值为3)
32.(2022·内蒙古通辽·统考小升初真题)工艺品厂要制作6000个中国结,前3天制作完成了总工作量的20%。照这样计算,还需要多少天全部制作完成?
33.(2022·内蒙古通辽·统考小升初真题)一个圆锥形沙堆,底面积是平方米,高是1.8米。把这堆沙铺在宽为5米,长为12米的路面上,厚度大约是多少厘米?(保留整厘米)
34.(2022·内蒙古通辽·统考小升初真题)一个长方形菜地的周长是160米,长比宽的2倍多8米,这块菜地的面积是多少平方米?
35.(2022·内蒙古通辽·统考小升初真题)李师傅要加工一批零件。他第一天完成了总数量的,第二天加工了200个,这两天共完成了总数的60%。这批零件一共有多少个?
36.(2022·内蒙古通辽·统考小升初真题)在一幅比例尺是1∶1000000的地图上,甲、乙两座城市相距5.2厘米。一辆轿车和一辆客车分别从甲城和乙城同时相向而行,轿车每小时行驶70千米,客车每小时行驶60千米。经过多长时间两车相遇?
37.(2022·内蒙古呼伦贝尔·统考小升初真题)这只工具箱的表面积是多少?(单位:分米)
38.(2022·内蒙古呼伦贝尔·统考小升初真题)根据下面的路线图,用自己的语言说说从学校到体育馆的路线。
39.(2022·广西百色·统考小升初真题)一根长2米,横截面直径是20厘米的木头浮在水面上,它正好是一半露出水面。
(1)这根木头的体积是多少立方厘米?
(2)这根木头与水接触的面积是多少平方厘米?
40.(2022·辽宁沈阳·统考小升初真题)体育用品商店。
(1)打折后,每个足球是多少元?
(2)笑笑和奇思共买了2个篮球、2副羽毛球拍和6个羽毛球,比打折前便宜多少元?
参考答案:
1.(1)16,24
(2)80名
(3)见详解
(4)见详解
【分析】(1)通过观察条形统计图可知,成绩及格的有16人,优秀的有24人;
(2)把抽测的人数看作单位“1”,其中及格的有16人,占抽测人数的20%,根据已知一个数的百分之几是多少,求这个数,用除法求出抽测的人数;
(3)再根据求一个数的百分之几是多少,用乘法求出不及格的人数,再根据减法的意义,用减法求出成绩良好的人数,据此补充条形统计图;
(4)根据求一个数是另一个数的百分之几,用除法求出优秀的占抽测人数的百分之几,用减法求出成绩良好的占抽测人数的百分之几,据此完成扇形统计图。
【详解】(1)成绩及格的有16人,优秀的有24人。
(2)16÷20%
=16÷0.2
=80(人)
答:六年级有80名学生参加了体能测试。
(3)80×5%=4(人)
80-(4+16+24)
=80-44
=36(人)
作图如下:
(4)优秀的占总人数的:
24÷80×100%
=0.3×100%
=30%
良好的占总人数的:
1-5%-20%-30%=45%
作图如下:
【点睛】此题考查的目的是理解掌握条形统计图、扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
2.220元
【分析】根据题意,八折就是80%,把衣服原价看作单位“1”,优惠了(1-80%),用500×(1-80%),求出优惠的钱数,500元大于360元,说明这件衣服优惠了120元,再加上打八折优惠的钱数,即可求出这件衣服优惠的钱数。
【详解】500×(1-80%)+120
=500×20%+120
=100+120
=220(元)
答:一共可以优惠220元。
【点睛】本题考查折扣问题,打几折就是百分之几十。
3.376.8平方厘米;653.12立方厘米
【分析】根据题意,求至少需要用多少彩纸,就是求这个圆柱形笔筒的表面积去掉一个底面的面积,根据圆柱的表面积公式:侧面积+底面积,代入数据,求出需要的彩纸的面积;再根据圆柱的体积公式:底面积×高,代入数据,即可解答。
【详解】3.14×(8÷2)2+3.14×8×13
=3.14×16+25.12×13
=50.24+326.56
=376.8(平方厘米)
3.14×(8÷2)2×13
=3.14×16×13
=50.24×13
=653.12(立方厘米)
答:至少需要用376.8平方厘米的彩纸,这个笔筒的体积是653.12立方厘米。
【点睛】利用圆柱的表面积公式、体积公式进行解答,关键是熟记公式。
4.52500元
【分析】根据利息=本金×利率×时间,代入数据,求出利息,再加上本金,即可解答。
【详解】五万=50000元
50000×2.50%×2+50000
=1250×2+50000
=2500+50000
=52500(元)
答:到期时可以取回52500元。
【点睛】本题考查利率问题,关键是熟记利息公式。
5.135.02平方米
【分析】求贴瓷砖的面积就是求圆柱的一个底面积和一个侧面积的和,利用S表=πr2+2πrh计算解答。
【详解】3.14×10×1.8+3.14×(10÷2)2
=31.4×1.8+3.14×25
=56.52+78.5
=135.02(平方米)
答:这个水池贴瓷砖的面积是135.02平方米。
【点睛】此题主要考查圆柱体的表面积,解答时一定要注意分清题目中的条件,灵活解答。
6.20千克
【分析】先把甲袋大米的质量看作单位“1”,取出后,再剩下(1-),根据分数乘法的意义,即可求出此时甲袋所剩大米的质量。再把甲袋所剩大米的质量平均分成8份,先用除法求出1份的质量,再用乘法求出3份的质量,即乙袋取出25%后剩大米的质量。再把乙袋原来大米的质量看作单位“1”,根据百分数除法的意义,用乙袋所剩大米的质量除以(1-25%),就是乙袋大米原来的质量。
【详解】60×(1-)÷8×3÷(1-25%)
=60×÷8×3÷75%
=20(千克)
答:乙袋中原来有20千克大米。
【点睛】关键是根据分数乘法的意义,求出甲袋取出后剩下的质量。除按上述解答方法外,也可把比转化成分数,求出乙袋取出25%后剩的质量,然后再根据百分数除法的意义,求乙袋原来的质量。
7.(1)(2)见详解;
(3)1∶4
【分析】(1)O点位置不变,确定出三角形另外两个顶点的位置,顺次连线。
(2)将图形②的底和高同时扩大到原来的2倍,画出扩大后的图形。
(3)分别求出图①与图③的面积,再写出它们的面积比。
【详解】(1)(2)如图:
(3)4×2÷2=4;
4×8÷2=16;
图①与图③的面积比是4∶16=1∶4。
【点睛】本题考查了图形的旋转、图形的放大与缩小,关键是能准确画图。
8.1470000平方米
【分析】把总面积看成单位“1”,用减法计算得出粮食作物种植面积占的百分率,总面积的20%对应的数量是42公顷,由此用除法求出总面积,再乘粮食作物种植面积占的百分率,即可得粮食作物种了多少平方米。
【详解】1-20%-10%=70%
42÷20%×70%
=210×70%
=147(公顷)
147公顷=1470000平方米
答:粮食作物种了1470000平方米。
【点睛】本题主要考查了扇形统计图,已知一个数的百分之几是多少,求这个数,用除法计算;已知一个数,求它的百分之几是多少,用乘法计算。
9.(1)0(2)右;左(3)4;﹣4(4)向西走5米;2米;图见详解
【分析】(1)0是正数和负数的分界点;据此解答;
(2)根据正负数在数轴上的位置,结合题干,直接填空即可;
(3)根据数轴上到原点的距离相等的数有两个,这两个数互为相反数的特点进行解答即可;
(4)用正负数表示意义相反的两种量:向东走记作正,则向西走就记作负,由此得解。
【详解】(1)0是正数和负数的分界点。
(2)所有的正数都在0的右边,所有的负数都在0的左边。
(3)在直线上,距0点4个单位长度的点分别是4和﹣4。
(4)这个人走﹣5米到B点表示向西走5米。
5-3=2(米)
这时他距离出发点有2米。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
10.30元
【分析】用故事书的标价5.4元乘5,再加上3元,求出这本字典的标价。
【详解】5.4×5+3
=27+3
=30(元)
答:这本字典标价30元。
【点睛】本题考查了小数乘法应用题,求一个数的几倍是多少,用这个数乘倍数。
11.(1)图见详解,(2,7);(2)(3)见详解
【分析】(1)圆心确定圆的位置,半径确定圆的大小,由此先将点A向上平移5格,再以平移后的点A为圆心,以2为半径即可画出这个平移后的图形,再利用数对表示位置的方法表示平移后A点的位置;
(2)用三角板的一条直角边的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和B点重合,过B沿直角边向已知直线a画直线即可;
(3)明确旋转中心以P点为旋转中心,确定旋转方向和角度,顺时针旋转90°,先描出旋转后的对应点再连线即可。
【详解】(1)画出将圆A向上平移5格后的图形①,平移后A点的位置用数对表示是(2,7)。
(1)(2)(3)作图如下:
【点睛】本题考查了图形的平移、旋转及垂线的画法,关键是画图要准确。
12.40%;6人
【分析】把该班总人数看作单位“1”,用减法计算即可得O型血的人数占全班人数的百分之几;用该班的总人数分别乘O型血的人数和A型血的人数占总人数的百分率,再相减即可。
【详解】1-24%-28%-8%
=76%-28%-8%
=40%
50×40%-50×28%
=20-14
=6(人)
答:O型血的人数占全班人数的40%,O型血的人数比A型血的人数多6人。
【点睛】此题主要考查的是如何从扇形统计图中获取信息,然后再根据信息进行计算的能力。
13.3202.8千克
【分析】观察图形可知,粮仓是一个底面直径是2米,高是1.5米的圆柱体和底面直径是2米,高是0.6米的圆锥体;根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×,代入数据,求出这个粮仓的体积,再乘600,即可解答,
【详解】3.14×(2÷2)2×1.5+3.14×(2÷2)2×0.6×
=3.14×1×1.5+3.14×1×0.6×
=3.14×1.5+3.14×0.6×
=4.71+1.884×
=4.71+0.628
=5.338(立方米)
5.338×600=3202.8(千克)
答:这个粮仓最多能装3202.8千克粮食。
【点睛】利用圆柱的体积公式、圆锥的体积公式进行解答,关键是熟记公式。
14.395.64毫升
【分析】根据图示可知,瓶子的容积包括高8厘米水的体积和高6厘米空白部分圆柱的体积,据此计算这两部分的体积和即可。
【详解】3.14×(6÷2)2×(8+6)
=3.14×9×14
=395.64(立方厘米)
395.64立方厘米=395.64毫升
答:这个饮料瓶的容积是395.64毫升。
【点睛】此题主要考查了圆柱体的体积公式的意义,及在生活中的实际应用。
15.(1)40;(2)8;(3)见详解
【分析】(1)把总人数看作单位“1”,其中自驾去参展的有20人,占总人数的50%,根据已知一个数的百分之几是多少,求这个数,用除法解答;(2)步行前往的占20%,根据求一个数的百分之几是多少,用乘法解答;(3)根据步行的人数,完成条形统计图。
【详解】(1)20÷50%=40(名)
(2)40×20%=8(名)
(3)条形统计图补充如下:
【点睛】本题主要考查的是理解掌握扇形统计图、条形统计图的特点及作用,解答本题的关键是根据统计图提供的信息,解决有关的实际问题。
16.1000元
【分析】医疗费-起付金额=报销部分,将报销部分看作单位“1”,报销部分×报销百分比=报销金额,医疗费-报销金额=自付金额,据此列式解答。
【详解】2800-(2800-400)×75%
=2800-2400×0.75
=2800-1800
=1000(元)
答:按规定王大伯自付1000元。
【点睛】关键是确定单位“1”,整体数量×部分对应百分率=部分数量。
17.(1)反
(2)25辆
【分析】(1)2.5×48=4×30=5×24=120,得出:车辆的载重量×所需车辆的数量=总重量,则车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例。
(2)设一共需要x辆卡车。因为车辆的载重量×所需车辆的数量=总重量(一定),所以4.8乘x的积等于2.5×48的积,据此即可解答。
【详解】(1)因为2.5×48=120(吨),4×30=120(吨),车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例。
(2)解:设一共需要x辆卡车。
4.8x=2.5×48
4.8x÷4.8=2.5×48÷4.8
x=25
答:一共需要25辆。
【点睛】本题考查了学生正反比例的判断情况,能运用统计表提供的信息解决问题。同时考查了学生理解分析问题的能力。
18.62.8立方分米
【分析】通过观察图形可知,把圆柱纵切成两半,表面积增加的是两个截面的面积,每个截面的长等于圆柱的高,每个截面的宽等于圆柱的底面直径,据此可以求出圆柱的底面直径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【详解】40÷2÷5
=20÷5
=4(分米)
3.14×(4÷2)2×5
=3.14×4×5
=12.56×5
=62.8(立方分米)
答:这个圆柱的体积是62.8立方分米。
【点睛】此题主要考查圆柱体积公式的灵活运用,关键是熟记公式,重点是求出圆柱的底面直径。
19.(1)200名
(2)见详解
(3)我发现了参加书法的人数占了总人数的10%,参加舞蹈的人数占总人数的15%,参加绘画的人数最多,参加书法的人数最少。(答案不唯一)
【分析】(1)根据图中的信息可知,绘画的人数是90人,占了总人数的45%,用绘画的人数除以绘画所占总人数的百分比即可;
(2)求出参加乐器的人数,再根据画条形统计图的方法,把图补充完整即可;
(3)根据图中所给的信息,分析数据写出的发现合理即可。
【详解】(1)90÷45%=200(名)
答:此次一共调查了200名学生。
(2)200-90-20-30
=110-20-30
=90-30
=60(人)
(3)我发现了参加书法的人数占了总人数的10%,参加舞蹈的人数占总人数的15%,参加绘画的人数最多,参加书法的人数最少。(答案不唯一)。
【点睛】此题考查了学生分析数据的能力和运算能力,考查了条形统计图、扇形统计图等知识。
20.2700套
【分析】设这批防护服的生产任务一共是x套,第一天生产的套数与总套数的比是1∶5,第一天生产x(套),根据等量关系:两天完成的套数=未完成的套数×(1-),列方程解答即可。
【详解】解:设这批防护服的生产任务一共是x套。
x+660=(x-x-660)×(1-)
x+660=(x-660)×
x+660=x-528
x=1188
x=2700
答:这批防护服的生产任务一共是2700套。
【点睛】本题主要考查了比及分数的应用,关键是根据等量关系:两天完成的套数=未完成的套数×(1-),列方程。
21.37.68立方分米
【分析】通过观察图形可知,把这个圆锥纵向切开,表面积增加的是两个切面的面积,每个切面的底等于圆锥的底面直径,每个切面的高等于圆锥的高,根据三角形的面积公式:S=ah÷2,那么h=2S÷a,据此求出圆锥的高,再根据圆锥的体积公式:V=,把数据代入公式解答。
【详解】24÷2=12(平方分米)
12×2÷(3×2)
=24÷6
=4(分米)
×3.14×32×4
=×3.14×9×4
=37.68(立方分米)
答:这个圆锥的体积是37.68立方分米。
【点睛】此题主要考查三角形的面积公式、圆锥的体积公式的灵活运用,关键是熟记公式,重点是求出圆锥的高。
22.(1)109.9平方米
(2)78.5立方米
【分析】(1)抹水泥的面是圆柱的底面和侧面,所以利用公式求出它的底面积和侧面积,再相加求出抹水泥的面积即可;
(2)根据圆柱的体积公式,代入数据求出这个水池能装水多少立方米。
【详解】(1)3.14×10×1+3.14×(10÷2)2
=3.14×10+3.14×25
=3.14×35
=109.9(平方米)
答:抹水泥的面积是109.9平方米。
(2)3.14×(10÷2)2×1
=3.14×25×1
=78.5(立方米)
答:这个水池能装水78.5立方米。
【点睛】本题考查了圆柱的表面积和体积,无盖圆柱表面积=底面积+侧面积,圆柱体积=底面积×高。
23.(1)见详解
(2)见详解
(3)20;10
【分析】根据数轴知识,分别标出A和B的位置即可,然后根据A和B距离0点的距离解答。
【详解】(1)
(2)30÷5=6(格)
6-4=2(格)
(3)A点离0点的距离分别是:
5×4=20(m)
B点离0点的距离分别是:
5×2=10(m)
【点睛】本题考查了数轴知识,结合题意解答即可。
24.62.8cm3
【分析】由题意分析可知,圆柱的底面直径是长方体底面的边长,即4厘米,高等于长方体的高,然后根据圆柱的体积公式进行计算即可。
【详解】3.14×(4÷2)2×5
=3.14×4×5
=62.8(立方厘米)
答:圆柱的体积是62.8立方厘米。
【点睛】本题主要考查长方体和圆柱的关系以及圆柱的体积公式。
25.正比例;15米
【分析】因为:影长÷杆长=每米杆子的影长(一定),所以影长和杆长成正比例。物体的长度和它的影子的长度的比值一定,即物体的长度和它的影子的长度的成正比例,由此列式解答即可。
【详解】“竿立而影现,喻收效迅速。”用数学的眼光来看,这是应用了比例知识中的正比例关系。
解:设旗杆的高度是x米,
x∶20=3∶4
4x=60
x=15
答:旗杆的高度是15米。
【点睛】解答此题的关键是,先判断题中的两种相关联的量成何比例,然后找准对应量,列式解答即可。
26.(1)157立方厘米
(2)5分钟
【分析】(1)由图形可以得到沙漏上部沙子的底面直径为10厘米,高为6厘米,如此利用圆锥的体积公式即可求出答案;
(2)根据上部沙漏沙子的体积可得其速度,再结合下部沙子的体积用除法求解即可。
【详解】(1)3.14×(10÷2)2×6×
=3.14×25×6×
=78.5×6×
=471×
=157(立方厘米)
答:沙漏上部沙子的体积是157立方厘米。
(2)157÷31.4=5(分钟)
答:漏完全部沙子需要5分钟。
【点睛】这是一道关于圆锥应用的题目,关键是掌握圆锥的体积公式。
27.138.6平方分米
【分析】因为底面直径是高的,高是8分米,所以底面直径为:10×=4(分米)。因为是无盖水桶,所以它的表面积等于圆柱的侧面积加上底面积即可。
【详解】10×=4(分米)
3.14×4×10+3.14×(4÷2)2
=125.6+12.56
=138.16(平方分米)
答:这个水桶至少要用铁皮138.6平方分米。
【点睛】本题的解答关键在于先求出底面直径,再根据圆柱的表面积公式即可解答。
28.A网店
【分析】A店打出七五折优惠,就是售价是原价的75%,用原价乘75%即可;B店打出每满100元减25元的优惠,320÷100=3(个)……20(元),320元里面最多有3个100元,可以减去3个25元;分别求出两个网店需要的钱数,然后再比较解答。
【详解】A店:320×75%=240(元);
B店:320÷100=3(个)……20(元);
320-25×3
=320-75
=245(元);
240<245;
答:到A网店购买更省钱。
【点睛】解答此题的关键是根据两个网店的促销活动,计算出每个网店需要花的钱数,然后再进行比较即可。
29.(1)2250立方米;(2)1520平方米
【分析】(1)需要挖土的体积就是这个游泳池的体积,用长方体的体积公式V=abh,解答即可。
(2)抹水泥的面积是长方体5个面的面积,缺少上面,则抹水泥的面积=长×宽+长×高×2+宽×高×2,据此解答。
【详解】(1)50÷2=25(米)
50×25×1.8=2250(立方米)
答:建这个游泳池共需挖土2250立方米。
(2)50×25+50×1.8×2+25×1.8×2
=1250+180+90
=1520(平方米)
答:抹水泥的面积是1520平方米。
【点睛】解答有关长方体表面积和体积的实际问题,一定要搞清所求的是什么,再进一步选择合理的计算方法解答问题。要熟练掌握并灵活运用长方体的表面积和体积公式。
30.(1)580人
(2)偏重:203人,偏轻:58人
(3)见详解
【分析】(1)把全校学生人数看作单位“1”,体重正常的学生有319人,占55%,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(2)根据求一个数的百分之几是多少,用乘法解答。
(3)根据统计图给出合理建议即可。(答案不唯一)
【详解】(1)319÷55%=580(人)
答:华苑小学共有学生580人。
(2)580×35%=203(人)
580×10%=58(人)
答:体重偏重的学生有203人,偏轻的学生有58人。
(3)建议体重偏重的同学,加强体育锻炼,少吃脂肪含量高的食物,建议体重偏轻的同学,不要挑食偏食,合理搭配食物,健康成长。(答案不唯一)
【点睛】此题考查的目的是理解掌握扇条统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
31.4.75厘米
【分析】阴影甲的面积=半圆的面积-空白部分的面积,阴影乙的面积=三角形ABC的面积-空白部分的面积,再根据阴影甲-阴影乙=2.5平方厘米,所以半圆的面积-空白部分的面积-(三角形ABC的面积-空白部分的面积)=2.5平方厘米,即半圆的面积-三角形ABC的面积=2.5平方厘米,利用圆和三角形的面积公式,代入数据求解即可。
【详解】3×(4÷2)2-4×BC÷2=2.5
3×4-2BC=2.5
12-2BC=2.5
2BC=12-2.5
2BC=9.5
BC=4.75
答:三角形中BC边长是4.75厘米。
【点睛】本题主要考查了组合图形的面积,解题的关键是把不规则图形转化为规则图形。
32.12天
【分析】3天就完成了20%,根据分数除法的意义,完成这些任务共需要(3÷20%)天,再减3天,即可得还需要多少天全部制作完成。
【详解】3÷20%-3
=15-3
=12(天)
答:还需要12天全部制作完成。
【点睛】本题主要考查了百分数的实际应用,已知一个数的百分之几是多少,求这个数,用除法计算。
33.16厘米
【分析】根据圆锥体积=底面积×高÷3,求出沙堆体积,再根据长方体的高=体积÷底面积,求出沙子厚度即可。
【详解】15.8×1.8÷3=9.48(立方米)
9.48÷(12×5)
=9.48÷60
=0.158(米)
≈16(厘米)
答:厚度大约是16厘米。
【点睛】关键是掌握并灵活运用长方体和圆锥体积公式。
34.1344平方米
【分析】用160÷2=80求出一组长与宽的和,再根据和倍问题用(80-8)÷(2+1)即可求出宽的长度,进而求出长。最后根据“长方形面积=长×宽”求出面积即可。
【详解】(160÷2-8)÷(2+1)
=72÷3
=24(米)
24×2+8
=48+8
=56(米)
56×24=1344(平方米)
答:这块菜地的面积是1344平方米。
【点睛】解答本题的关键是根据和倍问题先求出长和宽分别是多少,再进一步求出面积。
35.500个
【分析】将零件总数看作单位“1”,两天共完成的对应百分率-第一天完成的对应分率=第二天完成的对应分率或百分率,第二天完成数量÷对应分率或百分率=零件总数,据此列式解答。
【详解】200÷(60%-)
=200÷0.4
=500(个)
答:这批零件一共有500个。
【点睛】关键是确定单位“1”,部分数量÷对应分率或百分率=整体数量。
36.0.4小时
【分析】根据“实际距离=图上距离÷比例尺”解得甲乙两地的距离,然后根据“相遇时间=路程和÷速度和”求出两车的相遇时间。
【详解】1∶1000000=
5.2÷=5200000(厘米)
5200000厘米=52千米
52÷(70+60)
=52÷130
=0.4(小时)
答:经过0.4小时后两车相遇。
【点睛】本题主要考查的是实际距离和图上距离的转化,以及行程问题中的相遇问题,相遇时间=路程和÷速度和。
37.117.96平方分米
【分析】通过观察图形可知,上面的半圆柱求出一个底面的面积加上圆柱侧面积的一半,下面的长方体求它的5个面的面积,根据圆的面积公式:S=πr2,圆柱的侧面积公式:S=πdh,长方形的面积公式:S=a×b,把数据分别代入公式解答。
【详解】3.14×22+3.14×2×2×5÷2+5×4+5×3×2+4×3×2
=3.14×4+12.56×5÷2+20+30+24
=12.56+31.4+20+30+24
=63.96+30+24
=117.96(平方分米)
答:它的表面积是117.96平方分米。
【点睛】此题主要考查圆柱的表面积公式、长方体的表面积公式的灵活运用,关键是熟记公式。
38.学校到体育馆的路线:从学校向东走200米到文化宫,再向北偏东45°方向走400米到体育馆。
【详解】依据地图上的方向辨别方法,即“上北下南,左西右东”,即可描述出从学校到体育馆的路线。
【解答】
测出文化宫与体育馆之间的夹角是45°
测量出学校到文化宫图上距离2厘米,实际距离:
2÷=20000(厘米)
20000厘米=200米
测量出文化宫到体育馆图上距离4厘米,实际距离:
4÷=40000(厘米)
40000厘米=400米
所以学校到体育馆的路线:
从学校向东走200米到文化宫,再向北偏东45°方向走400米到体育馆。
【点睛】此题主要考查依据方向(角度)和距离判定物体位置的方法,首先要根据比例尺计算出实际距离,再根据图示说出路线。
39.(1)62800立方厘米;
(2)6594平方厘米
【分析】先计算出圆柱体木头的半径是多少,再把长2米转化为以厘米为单位的数。
(1)根据圆柱的体积=底面积×高进行计算即可得到答案;
(2)这根木头与水接触的面积就是这根圆柱体木头表面积的一半,可根据圆柱的表面积公式进行计算即可得到答案。
【详解】木头横截面的半径为:20÷2=10(厘米)
2米=200厘米
(1)3.14×102×200
=314×200
=62800(立方厘米)
答:这根木头的体积约是62800立方厘米。
(2)两个底面积:
3.14×102×2
=314×2
=628(平方厘米)
侧面积:
3.14×20×200
=62.8×200
=12560(平方厘米)
表面积:628+12560=13188(平方厘米)
与水接触的面积:13188÷2=6594(平方厘米)
答:这根木头与水接触的面积是6594平方厘米。
【点睛】充分结合示意图,展开空间思维,想象出木头与水接触的面的具体特征,是解题关键。
40.(1)57.6元
(2)58元
【分析】八折是指现价是原价的80%;
(1)把足球的原价看成单位“1”,用原价乘上80%就是打折后的单价;
(2)先求出2个篮球、2副羽毛球拍和6个羽毛球的价钱,然后把原价看成单位“1”,用原价乘上(1-80%)就是便宜的钱数。
【详解】(1)72×80%=57.6(元)
答:每个足球是57.6元。
(2)(96×2+40×2+3×6)×(1-80%)
=(192+80+18)×20%
=290×20%
=58(元)
答:比打折前便宜了58元。
【点睛】解决本题关键是理解打折的含义,再找出单位“1”,根据分数乘法的意义求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
