19。2。1矩形的性质[下学期]
文档属性
| 名称 | 19。2。1矩形的性质[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-19 00:00:00 | ||
图片预览






文档简介
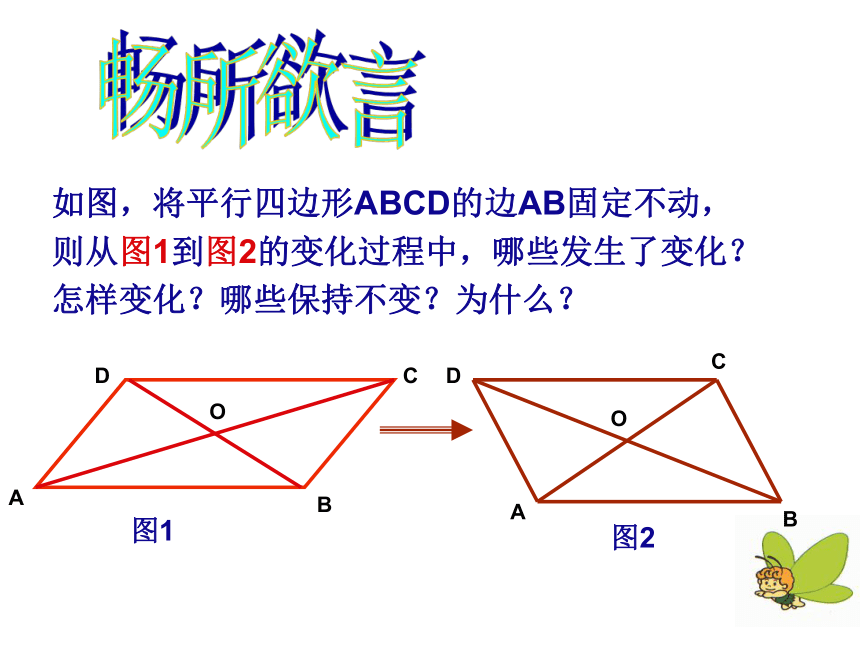
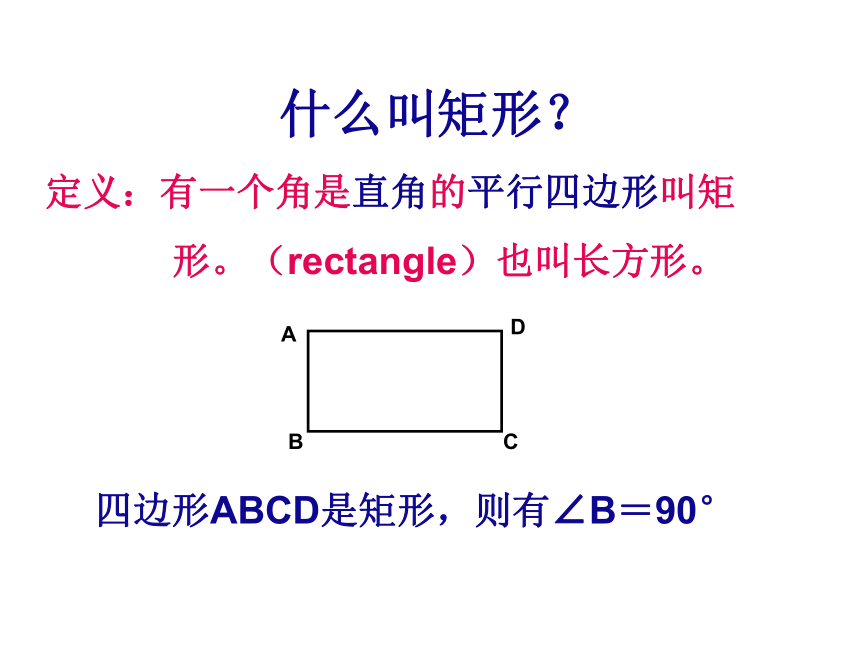
课件23张PPT。19.2特殊的平行四边形 畅所欲言如图,将平行四边形ABCD的边AB固定不动,则从图1到图2的变化过程中,哪些发生了变化?怎样变化?哪些保持不变?为什么?什么叫矩形?定义:有一个角是直角的平行四边形叫矩
形。(rectangle)也叫长方形。四边形ABCD是矩形,则有∠B=90°知识整合:平行四边形与矩形有什么关系?矩形是特殊的平行四边形,平行四边形包含矩形猜想:矩形有什么性质?命题1:矩形的四个角都是直角已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°命题2:矩形的对角线相等已知:四边形ABCD是矩形
求证:AC=BD证明:∵四边形ABCD是平行四边形
∴ AD=BC
又∵∠DAB=∠CBA=90°
在△ABC与△BAD中
∴△ABC≌△BAD
AC=BDAD=BC
∠DAB=∠CBA
AB=BA∴ODCBA相等的线段:AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD相等的角:∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB等腰三角形有:△OAB △ OBC △OCD △OAD直角三角形有:Rt△ABC Rt△BCD Rt△CDA Rt△DAB全等三角形有:Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB已知四边形ABCD是矩形有一个角是直角的
平行四边形叫矩形2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分 且相等1.矩形的定义:5.矩形是轴对称图形.3.直角三角形斜边上的中线等于斜边的一半4. 矩形的对角线把矩形分成两对全等的
等腰三角形总结例 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:∵四边形ABCD是矩形
∴ OA=OB
∵∠AOB=60° ∴△AOB是等边三角形
∴OA=AB=4(㎝)
∴矩形的对角线长 AC=BD=2OA=8(㎝)O 例2(补充)已知:如图 ,矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm.求AD的长及点A到BD的距离AE的长. 例3(补充) 已知:如图,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC. 求证:CE=EF.
证明:∵ 四边形ABCD是矩形,
∴ ∠B=90°,且AD∥BC. ∴ ∠1=∠2.
∵ DF⊥AE, ∴ ∠AFD=90°.
∴ ∠B=∠AFD.又 AD=AE,
∴ △ABE≌△DFA(AAS).
∴ AF=BE.
∴ EF=EC. 四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝550°10100°40°12482880°试一试试一试已知△ABC是Rt△,∠ABC=Rt∠,
BD是斜边AC上的中线若BD=3㎝则AC= ㎝
2 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝,∠BDC=6510120°如图,矩形的长与宽分别是2与1,以A为圆心AD为半径作DE弧,再以CD中点F为圆心,FC为半径作CE弧,则图中阴影部分面积为
阴影部分的面积是矩形面积的一半1例4,如图,锐角△ABC中,BE,CF是高,点M,N分别为
BC,EF的中点,求证:MN EF⊥开动脑筋 如图,在△ABC中,D,E,F,分别是BC、AC、AB边的中点,AH⊥BC于H,FD=8㎝,则HE=8㎝开动脑筋
你能将下列的矩形分割成三个面积相等的小矩形吗?你有几种方法?这
堂
课
你
学
到
了
什
么?回味无穷
形。(rectangle)也叫长方形。四边形ABCD是矩形,则有∠B=90°知识整合:平行四边形与矩形有什么关系?矩形是特殊的平行四边形,平行四边形包含矩形猜想:矩形有什么性质?命题1:矩形的四个角都是直角已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°命题2:矩形的对角线相等已知:四边形ABCD是矩形
求证:AC=BD证明:∵四边形ABCD是平行四边形
∴ AD=BC
又∵∠DAB=∠CBA=90°
在△ABC与△BAD中
∴△ABC≌△BAD
AC=BDAD=BC
∠DAB=∠CBA
AB=BA∴ODCBA相等的线段:AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD相等的角:∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB等腰三角形有:△OAB △ OBC △OCD △OAD直角三角形有:Rt△ABC Rt△BCD Rt△CDA Rt△DAB全等三角形有:Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB已知四边形ABCD是矩形有一个角是直角的
平行四边形叫矩形2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分 且相等1.矩形的定义:5.矩形是轴对称图形.3.直角三角形斜边上的中线等于斜边的一半4. 矩形的对角线把矩形分成两对全等的
等腰三角形总结例 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:∵四边形ABCD是矩形
∴ OA=OB
∵∠AOB=60° ∴△AOB是等边三角形
∴OA=AB=4(㎝)
∴矩形的对角线长 AC=BD=2OA=8(㎝)O 例2(补充)已知:如图 ,矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm.求AD的长及点A到BD的距离AE的长. 例3(补充) 已知:如图,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC. 求证:CE=EF.
证明:∵ 四边形ABCD是矩形,
∴ ∠B=90°,且AD∥BC. ∴ ∠1=∠2.
∵ DF⊥AE, ∴ ∠AFD=90°.
∴ ∠B=∠AFD.又 AD=AE,
∴ △ABE≌△DFA(AAS).
∴ AF=BE.
∴ EF=EC. 四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝550°10100°40°12482880°试一试试一试已知△ABC是Rt△,∠ABC=Rt∠,
BD是斜边AC上的中线若BD=3㎝则AC= ㎝
2 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝,∠BDC=6510120°如图,矩形的长与宽分别是2与1,以A为圆心AD为半径作DE弧,再以CD中点F为圆心,FC为半径作CE弧,则图中阴影部分面积为
阴影部分的面积是矩形面积的一半1例4,如图,锐角△ABC中,BE,CF是高,点M,N分别为
BC,EF的中点,求证:MN EF⊥开动脑筋 如图,在△ABC中,D,E,F,分别是BC、AC、AB边的中点,AH⊥BC于H,FD=8㎝,则HE=8㎝开动脑筋
你能将下列的矩形分割成三个面积相等的小矩形吗?你有几种方法?这
堂
课
你
学
到
了
什
么?回味无穷
