2023年中考数学专题冲刺针对复习测试卷:三角形(含答案)
文档属性
| 名称 | 2023年中考数学专题冲刺针对复习测试卷:三角形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 183.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 14:42:58 | ||
图片预览


文档简介
专题冲刺针对复习测试卷:三角形
(时间:60分钟 分数:100分)
姓名: 班级: 学号: 分数:
选择题(本题共8小题,共40分)
1.(2022·江苏宿迁)若等腰三角形的两边长分别是3cm和5cm,则这个等腰三角形的周长是( )
A.8cm B.13cm C.8cm或13cm D.11cm或13cm
2.(2022·广西贺州)如图,在Rt△ABC中,∠C=90°,∠B=56°,则∠A的度数为( )
A. B. C. D.
3.(2020 福建)如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5 C.4 D.3
4.(2020 聊城)如图,在△ABC中,AB=AC,∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是( )
A.120° B.130° C.145° D.150°
5.(2020·湖南益阳)如图,在中,的垂直平分线交于点,平分,若,则的度数为( )
A. B. C. D.
6.(2020 河北)如图,从笔直的公路l旁一点P出发,向西走6km到达l;从P出发向北走6km也到达l.下列说法错误的是( )
A.从点P向北偏西45°走3km到达l
B.公路l的走向是南偏西45°
C.公路l的走向是北偏东45°
D.从点P向北走3km后,再向西走3km到达l
7.(2020·广西贺州)如图,将两个完全相同的Rt△ACB和Rt△A'C′B′拼在一起,其中点A′与点B重合,点C'在边AB上,连接B′C,若∠ABC=∠A′B′C′=30°,AC=A′C′=2,则B′C的长为( )
A.2 B.4 C.2 D.4
8.(2020 内江)如图,在△ABC中,D、E分别是AB和AC的中点,S四边形BCED=15,则S△ABC=( )
A.30 B.25 C.22.5 D.20
填空题(本题共5小题,每空3分,共15分)
9.(2021·辽宁本溪)如图,在中,,由图中的尺规作图痕迹得到的射线与交于点E,点F为的中点,连接,若,则的周长为_______.
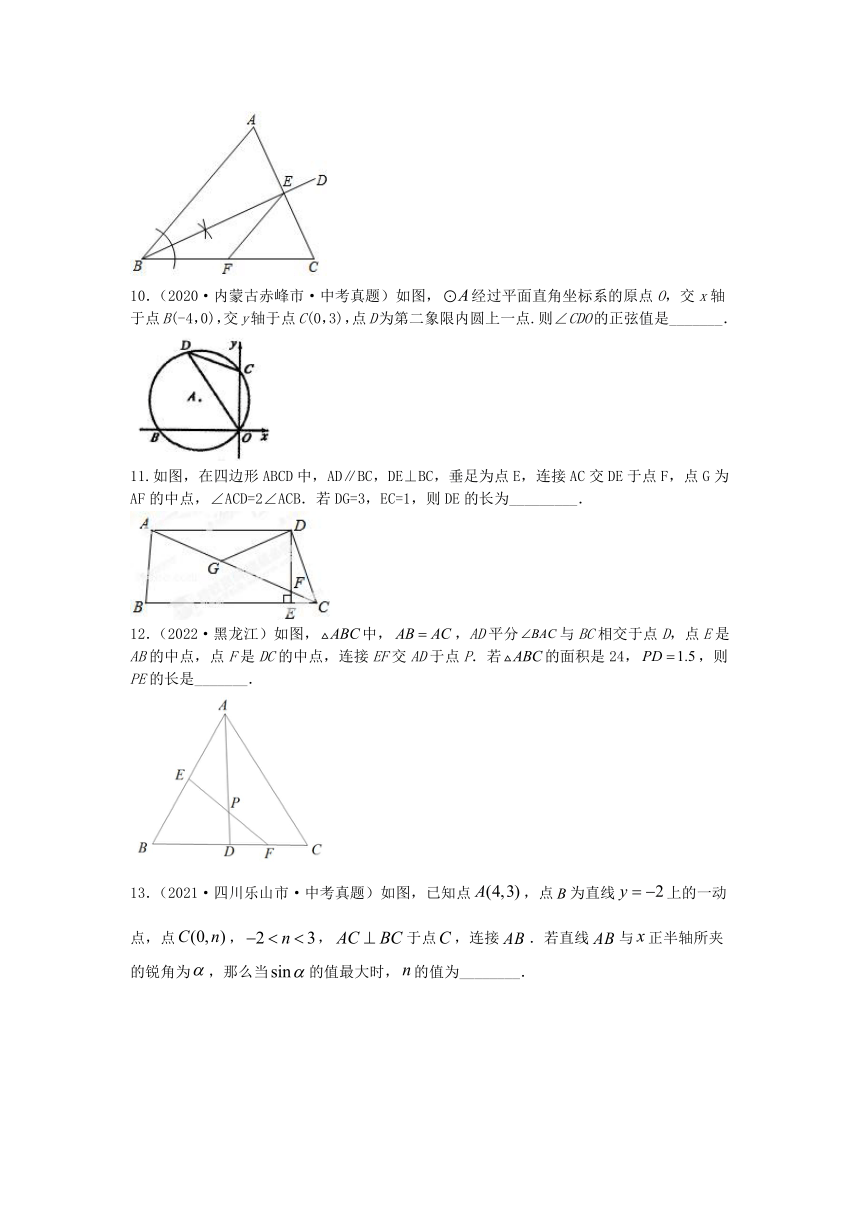
10.(2020·内蒙古赤峰市·中考真题)如图,经过平面直角坐标系的原点O,交x轴于点B(-4,0),交y轴于点C(0,3),点D为第二象限内圆上一点.则∠CDO的正弦值是_______.
11.如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为_________.
12.(2022·黑龙江)如图,中,,AD平分与BC相交于点D,点E是AB的中点,点F是DC的中点,连接EF交AD于点P.若的面积是24,,则PE的长是_______.
13.(2021·四川乐山市·中考真题)如图,已知点,点为直线上的一动点,点,,于点,连接.若直线与正半轴所夹的锐角为,那么当的值最大时,的值为________.
解答题(本题共3小题,共45分)
14.如图,AC平分∠BAD,AB=AD.求证:BC=DC.
15.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
16.(2021·贵州黔西)如图1,D为等边△ABC内一点,将线段AD绕点A逆时针旋转60°得到AE,连接CE,BD的延长线与AC交于点G,与CE交于点F.
(1)求证:BD=CE;
(2)如图2,连接FA,小颖对该图形进行探究,得出结论:∠BFC=∠AFB=∠AFE.小颖的结论是否正确?若正确,请给出证明;若不正确,请说明理由.
参考答案:
1.D 2.A 3.B 4.B 5.B 6.A 7.A 8.D
9.
10.
11.
12.2.5
13.
14.证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,
又∵AB=AD,AC=AC,
∴△ABC≌△ADC(SAS),
∴BC=CD.
15.(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴AB=CD;
(2)解:∵△ABE≌△DCF,
∴AB=CD,BE=CF,∠B=∠C,
∵∠B=40°,
∴∠C=40°
∵AB=CF,
∴CF=CD,
∴∠D=∠CFD(180°﹣40°)=70°.
16.解:证明:(1)如图1,∵线段AD绕点A逆时针旋转60°得到AE,
∴AD=AE,∠DAE=60°,
∵∠BAC=60°,
∴∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
(2)由(1)可知△ABD≌△ACE
则∠ABD=∠ACE,
又∵∠AGB=∠CGF,
∴∠BFC=∠BAC=60°,
∴∠BFE=120°,
过A作BD,CF的垂线段分别交于点M,N,
又∵△ABD≌△ACE,BD=CE,
∴由面积相等可得AM=AN,
在Rt△AFM和Rt△AFN中,
,
∴Rt△AFM≌Rt△AFN(HL),
∴∠AFM=∠AFN,
∴∠BFC=∠AFB=∠AFE=60°.
(时间:60分钟 分数:100分)
姓名: 班级: 学号: 分数:
选择题(本题共8小题,共40分)
1.(2022·江苏宿迁)若等腰三角形的两边长分别是3cm和5cm,则这个等腰三角形的周长是( )
A.8cm B.13cm C.8cm或13cm D.11cm或13cm
2.(2022·广西贺州)如图,在Rt△ABC中,∠C=90°,∠B=56°,则∠A的度数为( )
A. B. C. D.
3.(2020 福建)如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5 C.4 D.3
4.(2020 聊城)如图,在△ABC中,AB=AC,∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是( )
A.120° B.130° C.145° D.150°
5.(2020·湖南益阳)如图,在中,的垂直平分线交于点,平分,若,则的度数为( )
A. B. C. D.
6.(2020 河北)如图,从笔直的公路l旁一点P出发,向西走6km到达l;从P出发向北走6km也到达l.下列说法错误的是( )
A.从点P向北偏西45°走3km到达l
B.公路l的走向是南偏西45°
C.公路l的走向是北偏东45°
D.从点P向北走3km后,再向西走3km到达l
7.(2020·广西贺州)如图,将两个完全相同的Rt△ACB和Rt△A'C′B′拼在一起,其中点A′与点B重合,点C'在边AB上,连接B′C,若∠ABC=∠A′B′C′=30°,AC=A′C′=2,则B′C的长为( )
A.2 B.4 C.2 D.4
8.(2020 内江)如图,在△ABC中,D、E分别是AB和AC的中点,S四边形BCED=15,则S△ABC=( )
A.30 B.25 C.22.5 D.20
填空题(本题共5小题,每空3分,共15分)
9.(2021·辽宁本溪)如图,在中,,由图中的尺规作图痕迹得到的射线与交于点E,点F为的中点,连接,若,则的周长为_______.
10.(2020·内蒙古赤峰市·中考真题)如图,经过平面直角坐标系的原点O,交x轴于点B(-4,0),交y轴于点C(0,3),点D为第二象限内圆上一点.则∠CDO的正弦值是_______.
11.如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为_________.
12.(2022·黑龙江)如图,中,,AD平分与BC相交于点D,点E是AB的中点,点F是DC的中点,连接EF交AD于点P.若的面积是24,,则PE的长是_______.
13.(2021·四川乐山市·中考真题)如图,已知点,点为直线上的一动点,点,,于点,连接.若直线与正半轴所夹的锐角为,那么当的值最大时,的值为________.
解答题(本题共3小题,共45分)
14.如图,AC平分∠BAD,AB=AD.求证:BC=DC.
15.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
16.(2021·贵州黔西)如图1,D为等边△ABC内一点,将线段AD绕点A逆时针旋转60°得到AE,连接CE,BD的延长线与AC交于点G,与CE交于点F.
(1)求证:BD=CE;
(2)如图2,连接FA,小颖对该图形进行探究,得出结论:∠BFC=∠AFB=∠AFE.小颖的结论是否正确?若正确,请给出证明;若不正确,请说明理由.
参考答案:
1.D 2.A 3.B 4.B 5.B 6.A 7.A 8.D
9.
10.
11.
12.2.5
13.
14.证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,
又∵AB=AD,AC=AC,
∴△ABC≌△ADC(SAS),
∴BC=CD.
15.(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴AB=CD;
(2)解:∵△ABE≌△DCF,
∴AB=CD,BE=CF,∠B=∠C,
∵∠B=40°,
∴∠C=40°
∵AB=CF,
∴CF=CD,
∴∠D=∠CFD(180°﹣40°)=70°.
16.解:证明:(1)如图1,∵线段AD绕点A逆时针旋转60°得到AE,
∴AD=AE,∠DAE=60°,
∵∠BAC=60°,
∴∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
(2)由(1)可知△ABD≌△ACE
则∠ABD=∠ACE,
又∵∠AGB=∠CGF,
∴∠BFC=∠BAC=60°,
∴∠BFE=120°,
过A作BD,CF的垂线段分别交于点M,N,
又∵△ABD≌△ACE,BD=CE,
∴由面积相等可得AM=AN,
在Rt△AFM和Rt△AFN中,
,
∴Rt△AFM≌Rt△AFN(HL),
∴∠AFM=∠AFN,
∴∠BFC=∠AFB=∠AFE=60°.
同课章节目录
