江苏省无锡市第一中学2006—2007学年度上学期高一质量测试数学--苏教版[上学期]
文档属性
| 名称 | 江苏省无锡市第一中学2006—2007学年度上学期高一质量测试数学--苏教版[上学期] | 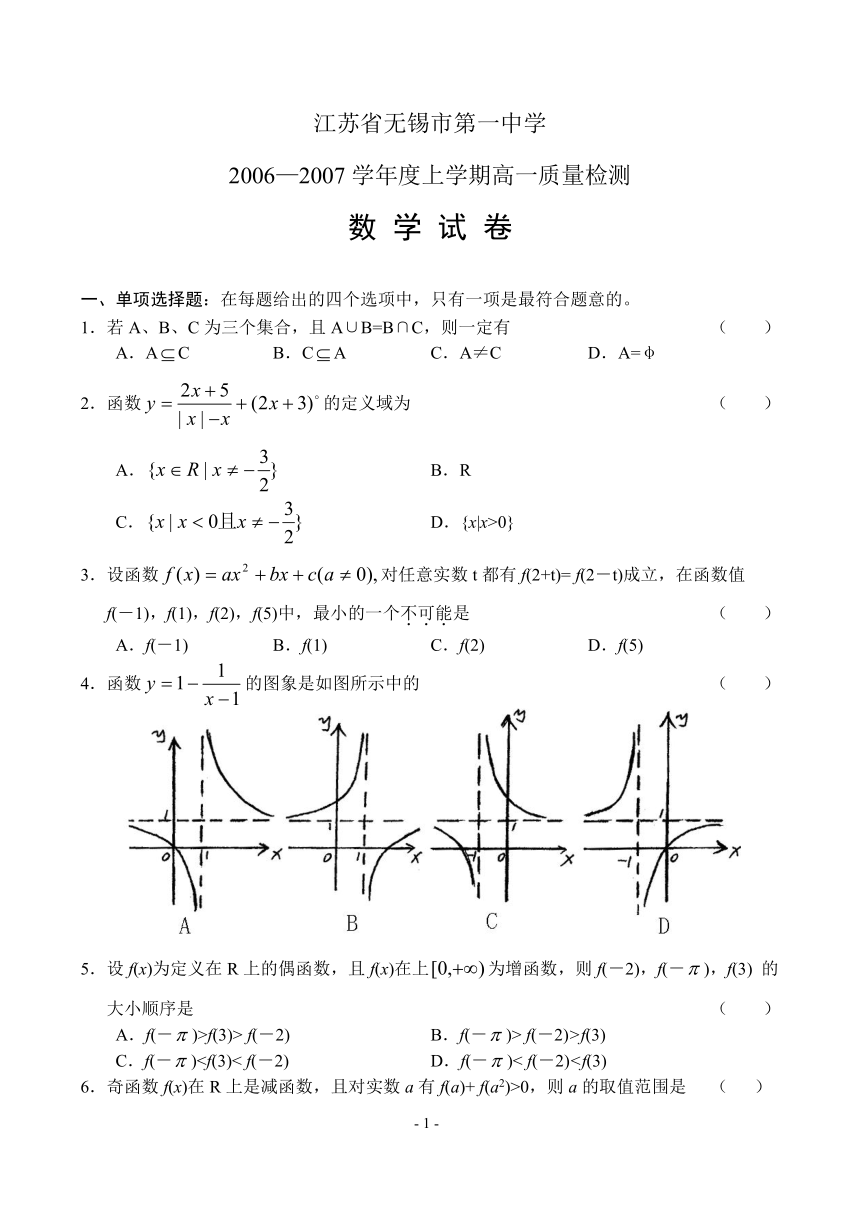 | |
| 格式 | zip | ||
| 文件大小 | 132.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-21 15:01:00 | ||
图片预览



文档简介
5
江苏省无锡市第一中学
2006—2007学年度上学期高一质量检测
数 学 试 卷
一、单项选择题:在每题给出的四个选项中,只有一项是最符合题意的。
1.若A、B、C为三个集合,且A∪B=B∩C,则一定有 ( )
A.AC B.CA C.A≠C D.A=φ
2.函数的定义域为 ( )
A. B.R
C. D.{x|x>0}
3.设函数对任意实数t都有f(2+t)= f(2-t)成立,在函数值
f(-1),f(1),f(2),f(5)中,最小的一个不可能是 ( )
A.f(-1) B.f(1) C.f(2) D.f(5)
4.函数的图象是如图所示中的 ( )
5.设f(x)为定义在R上的偶函数,且f(x)在上为增函数,则f(-2),f(-),f(3) 的
大小顺序是 ( )
A.f(-)>f(3)> f(-2) B.f(-)> f(-2)>f(3)
C.f(-)6.奇函数f(x)在R上是减函数,且对实数a有f(a)+ f(a2)>0,则a的取值范围是 ( )
A.(-∞,-1) B.(1,+∞) C.(0,1) D.(-1,0)
7.若奇函数y= f(x)(x≠0),在x∈(0,+∞)时,f(x)=x-1,那么使f(x-1)<0的x的集合为
( )
A.{x|18.已知定义在R上的函数f(x)满足f(x+y)= f(x)+f(y),则f(x)一定是 ( )
A.奇函数 B.偶函数 C.既奇又偶函数 D.非奇非偶函数
二、填空题:
9.函数的值域为
10.函数上具有单调性,则a的取值范围是
11.已知函数y=f(x)是R上奇函数,且当x>0时,f(x)=1,则函数y=f(x)的表达式是
12.现代社会对破译密码的难度要求越来越高,有一处密码把英文的明文(真实名)按字母分解,其中英文a,b,c…,z这26个字母(不论大小写)依次对应1,2,3…,26这26个正整数。(见下表)
a b c d e f g h i j k l M
1 2 3 4 5 6 7 8 9 10 11 12 13
n o p q r s t u v w x y z
14 15 16 17 18 19 20 21 22 23 24 25 26
用如下变换公式:将明文转换成密码,如,即y变成m;
按上述变换规则,若将明文译成的密码是live,那么原来的明文是
三、解答题:
13.设全集U=R,且AB,
求实数a的取值范围.
14.已知f(x)是一个定义在R上的函数,求证:
(1)g(x)= f(x)+ f(-x)是偶函数;
(2)h(x)= f(x)-f(-x)是奇函数.
15.已知f(x)是二次函数,且f(0)=0,f(x+1)= f(x)+x+1,
(1)求f(x)的表达式;
(2)若f(x)>a在x∈[-1,1]恒成立,求实数a的取值范围;
16.建造一个容积为8m3、深为2m的长方体形无盖游泳池,如果池底和池壁的造价分别为
120元/m2和80元/m2。
(1)求总造价y(元)关于底面一边长x(m)的函数解析式,并指出该函数的定义域;
(2)在定义域范围内求出总造价的最小值。
(如利用函数单调性求最小值的,请用定义证明单调性)
参考答案
一、选择题:
1.A 2.C 3.B 4.B 5.A 6.D 7.C 8.A
二、填空题:
9. 10. 11.12.wqri
三、解答题:
13.解:
∴实数a的取值范围[1,3]
14.证:(1)
∴g(x)是R上的偶函数
∴h(x)是-R上的奇函数.
15.证:(1)设
(2)
16.解:(1)
定义域(0,+∞)
(2)设
设
∴f(x)在上是减函数,f(x)在(2,+∞)上是增函数
∴当x=2时,f(x)min=f(2)=1760(元)
答:在定义域范围内总造价的最小值为1760元.
PAGE
- 1 -
江苏省无锡市第一中学
2006—2007学年度上学期高一质量检测
数 学 试 卷
一、单项选择题:在每题给出的四个选项中,只有一项是最符合题意的。
1.若A、B、C为三个集合,且A∪B=B∩C,则一定有 ( )
A.AC B.CA C.A≠C D.A=φ
2.函数的定义域为 ( )
A. B.R
C. D.{x|x>0}
3.设函数对任意实数t都有f(2+t)= f(2-t)成立,在函数值
f(-1),f(1),f(2),f(5)中,最小的一个不可能是 ( )
A.f(-1) B.f(1) C.f(2) D.f(5)
4.函数的图象是如图所示中的 ( )
5.设f(x)为定义在R上的偶函数,且f(x)在上为增函数,则f(-2),f(-),f(3) 的
大小顺序是 ( )
A.f(-)>f(3)> f(-2) B.f(-)> f(-2)>f(3)
C.f(-)
A.(-∞,-1) B.(1,+∞) C.(0,1) D.(-1,0)
7.若奇函数y= f(x)(x≠0),在x∈(0,+∞)时,f(x)=x-1,那么使f(x-1)<0的x的集合为
( )
A.{x|1
A.奇函数 B.偶函数 C.既奇又偶函数 D.非奇非偶函数
二、填空题:
9.函数的值域为
10.函数上具有单调性,则a的取值范围是
11.已知函数y=f(x)是R上奇函数,且当x>0时,f(x)=1,则函数y=f(x)的表达式是
12.现代社会对破译密码的难度要求越来越高,有一处密码把英文的明文(真实名)按字母分解,其中英文a,b,c…,z这26个字母(不论大小写)依次对应1,2,3…,26这26个正整数。(见下表)
a b c d e f g h i j k l M
1 2 3 4 5 6 7 8 9 10 11 12 13
n o p q r s t u v w x y z
14 15 16 17 18 19 20 21 22 23 24 25 26
用如下变换公式:将明文转换成密码,如,即y变成m;
按上述变换规则,若将明文译成的密码是live,那么原来的明文是
三、解答题:
13.设全集U=R,且AB,
求实数a的取值范围.
14.已知f(x)是一个定义在R上的函数,求证:
(1)g(x)= f(x)+ f(-x)是偶函数;
(2)h(x)= f(x)-f(-x)是奇函数.
15.已知f(x)是二次函数,且f(0)=0,f(x+1)= f(x)+x+1,
(1)求f(x)的表达式;
(2)若f(x)>a在x∈[-1,1]恒成立,求实数a的取值范围;
16.建造一个容积为8m3、深为2m的长方体形无盖游泳池,如果池底和池壁的造价分别为
120元/m2和80元/m2。
(1)求总造价y(元)关于底面一边长x(m)的函数解析式,并指出该函数的定义域;
(2)在定义域范围内求出总造价的最小值。
(如利用函数单调性求最小值的,请用定义证明单调性)
参考答案
一、选择题:
1.A 2.C 3.B 4.B 5.A 6.D 7.C 8.A
二、填空题:
9. 10. 11.12.wqri
三、解答题:
13.解:
∴实数a的取值范围[1,3]
14.证:(1)
∴g(x)是R上的偶函数
∴h(x)是-R上的奇函数.
15.证:(1)设
(2)
16.解:(1)
定义域(0,+∞)
(2)设
设
∴f(x)在上是减函数,f(x)在(2,+∞)上是增函数
∴当x=2时,f(x)min=f(2)=1760(元)
答:在定义域范围内总造价的最小值为1760元.
PAGE
- 1 -
