1.4.3 整式的乘法(第3课时)(北师大版七年级下册)
文档属性
| 名称 | 1.4.3 整式的乘法(第3课时)(北师大版七年级下册) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-15 23:08:10 | ||
图片预览







文档简介
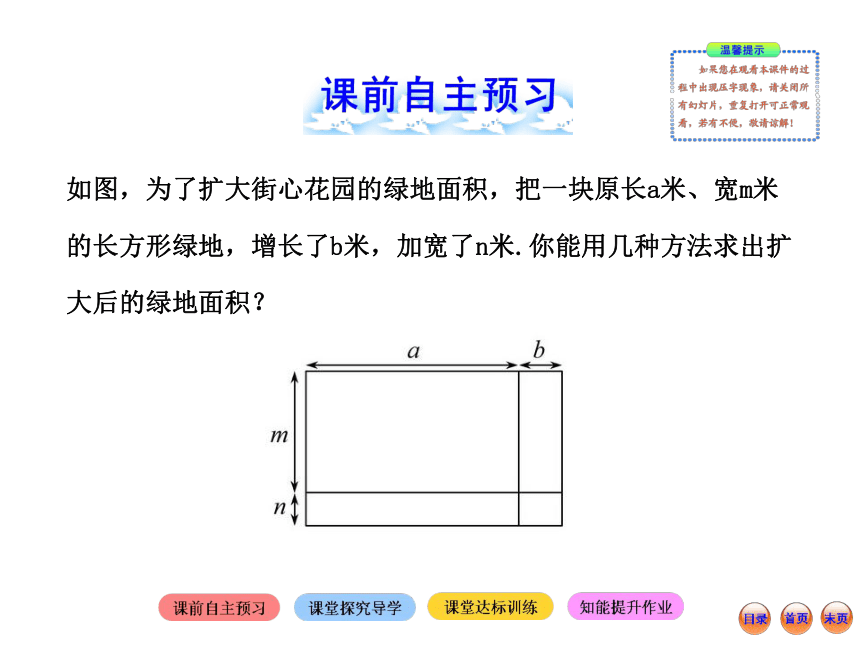
课件20张PPT。第3课时如图,为了扩大街心花园的绿地面积,把一块原长a米、宽m米的长方形绿地,增长了b米,加宽了n米.你能用几种方法求出扩大后的绿地面积?方法一:这块花园现在长______米,宽______米,因而面积为
___________平方米.
方法二:这块花园现在是由___小块组成,它们的面积分别为:
___平方米、___平方米、___平方米、___平方米,故这块绿地
的面积为______________平方米.
由此可得:___________和____________表示的是同一块绿地面
积.所以有_______________________.(a+b)(m+n)(a+b)(m+n)四amanbmbn(am+an+bm+bn)(a+b)(m+n)am+an+bm+bn(a+b)(m+n)=am+an+bm+bn【归纳】多项式与多项式相乘,先用一个多项式的_______乘另
一个多项式的_______,再把所得的积_____.
【点拨】多项式乘以多项式的法则,体现了数学的转化思想,即多项式乘以多项式转化为单项式乘以多项式,最后转化为单项式乘以单项式.每一项每一项相加【预习思考】
多项式与多项式相乘,在合并同类项之前,积的项数和两个多项式的项数有什么关系?
提示:在合并之前积的项数等于两个多项式的项数之积. 多项式乘以多项式
【例】(8分)计算:(1)(-2x-1)·(3x-1).
(2)(a+1)(a2-a+1).【规范解答】
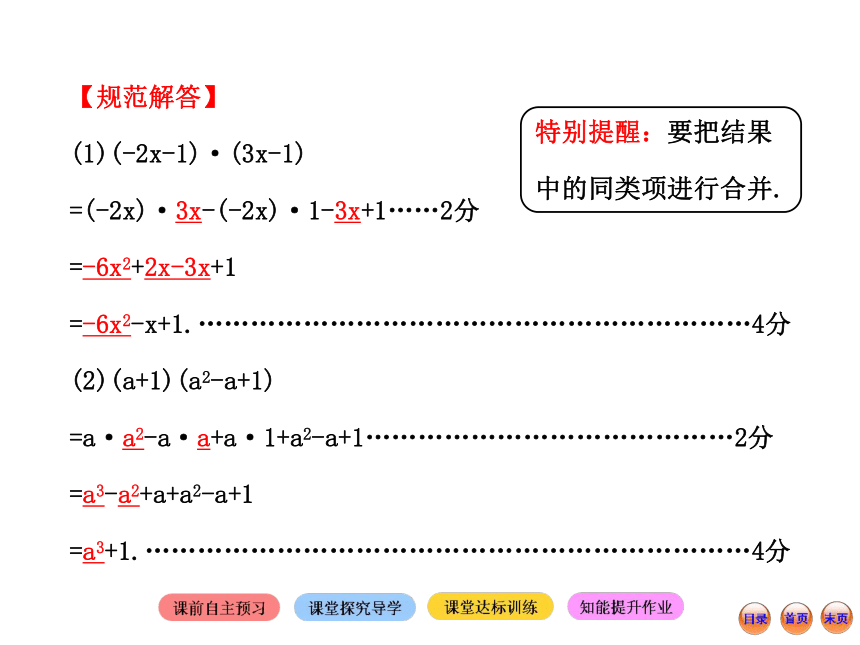
(1)(-2x-1)·(3x-1)
=(-2x)·3x-(-2x)·1-3x+1……2分
=-6x2+2x-3x+1
=-6x2-x+1.………………………………………………………4分
(2)(a+1)(a2-a+1)
=a·a2-a·a+a·1+a2-a+1……………………………………2分
=a3-a2+a+a2-a+1
=a3+1.……………………………………………………………4分特别提醒:要把结果中的同类项进行合并.【规律总结】
多项式乘以多项式的“三点注意”
(1)一定要按照一定的顺序相乘,做到不重不漏.
(2)计算时,一定要注意符号问题,每一项都包含前面的符号.
(3)如果结果中有同类项,一定要合并同类项.【跟踪训练】
1.(x-1)(2x+3)的计算结果是( )
(A)2x2+x-3 (B)2x2-x-3
(C)2x2-x+3 (D)x3-2x-3
【解析】选A.(x-1)(2x+3)=2x2+3x-2x-3
=2x2+x-3.2.若(x+4)(x-3)=x2+mx-n,则( )
(A)m=-1,n=12 (B)m=-1,n=-12
(C)m=1,n=-12 (D)m=1,n=12
【解析】选D.因为(x+4)(x-3)=x2+x-12,
而(x+4)(x-3)=x2+mx-n,
所以x2+x-12=x2+mx-n,所以m=1,n=12.【变式备选】若(x+3)(x+n)=x2+mx-15,则m的值为( )
(A)-5 (B)5 (C)-2 (D)2
【解析】选C.因为(x+3)(x+n)=x2+(3+n)x+3n
=x2+mx-15,所以3+n=m,3n=-15,解得n=-5,m=-5+3=-2.3.计算:(a-2b)(2a-b)=_____.
【解析】(a-2b)(2a-b)=2a2-ab-4ab+2b2
=2a2-5ab+2b2.
答案:2a2-5ab+2b24.解方程:8x2-(2x-3)(4x+2)=14.
【解析】8x2-(2x-3)(4x+2)=14,
8x2-(8x2+4x-12x-6)=14,
8x2-8x2-4x+12x+6=14,
8x=8,
x=1.1.下列各式中,计算结果是a2-3a-40的是( )
(A)(a+4)(a-10) (B)(a-4)(a+10)
(C)(a-5)(a+8) (D)(a+5)(a-8)
【解析】选D.(a+4)(a-10)=a2-6a-40;(a-4)(a+10)=a2+6a-40; (a-5)(a+8)=a2+3a-40;(a+5)(a-8)=a2-3a-40.2.长方形一边长3m+2n,另一边比它长m-n,则这个长方形面积是( )
(A)12m2+11mn+2n2 (B)12m2+5mn+2n2
(C)12m2-5mn+2n2 (D)12m2+11mn+n2
【解析】选A.由题意知,另一边的长为3m+2n+m-n=4m+n,
所以这个长方形的面积是(3m+2n)(4m+n)=12m2+11mn+2n2.3.若(x+m)(x+3)整理后结果中不含x的一次项,则m的值为_____.
【解析】因为(x+m)(x+3)=x2+(m+3)x+3m,又因为结果中不含x的一次项,所以m+3=0,解得m=-3.
答案:-34.若(x+6)(x+2)=x(x-3)-21,则x=_____.
【解析】因为(x+6)(x+2)=x2+8x+12,x(x-3)-21=x2-3x-21,所以x2+8x+12=x2-3x-21,所以11x=-33,x=-3.
答案:-35.(2012·安徽中考)计算:(a+3)(a-1)+a(a-2).
【解析】原式=a2-a+3a-3+a2-2a
=2a2-3.
___________平方米.
方法二:这块花园现在是由___小块组成,它们的面积分别为:
___平方米、___平方米、___平方米、___平方米,故这块绿地
的面积为______________平方米.
由此可得:___________和____________表示的是同一块绿地面
积.所以有_______________________.(a+b)(m+n)(a+b)(m+n)四amanbmbn(am+an+bm+bn)(a+b)(m+n)am+an+bm+bn(a+b)(m+n)=am+an+bm+bn【归纳】多项式与多项式相乘,先用一个多项式的_______乘另
一个多项式的_______,再把所得的积_____.
【点拨】多项式乘以多项式的法则,体现了数学的转化思想,即多项式乘以多项式转化为单项式乘以多项式,最后转化为单项式乘以单项式.每一项每一项相加【预习思考】
多项式与多项式相乘,在合并同类项之前,积的项数和两个多项式的项数有什么关系?
提示:在合并之前积的项数等于两个多项式的项数之积. 多项式乘以多项式
【例】(8分)计算:(1)(-2x-1)·(3x-1).
(2)(a+1)(a2-a+1).【规范解答】
(1)(-2x-1)·(3x-1)
=(-2x)·3x-(-2x)·1-3x+1……2分
=-6x2+2x-3x+1
=-6x2-x+1.………………………………………………………4分
(2)(a+1)(a2-a+1)
=a·a2-a·a+a·1+a2-a+1……………………………………2分
=a3-a2+a+a2-a+1
=a3+1.……………………………………………………………4分特别提醒:要把结果中的同类项进行合并.【规律总结】
多项式乘以多项式的“三点注意”
(1)一定要按照一定的顺序相乘,做到不重不漏.
(2)计算时,一定要注意符号问题,每一项都包含前面的符号.
(3)如果结果中有同类项,一定要合并同类项.【跟踪训练】
1.(x-1)(2x+3)的计算结果是( )
(A)2x2+x-3 (B)2x2-x-3
(C)2x2-x+3 (D)x3-2x-3
【解析】选A.(x-1)(2x+3)=2x2+3x-2x-3
=2x2+x-3.2.若(x+4)(x-3)=x2+mx-n,则( )
(A)m=-1,n=12 (B)m=-1,n=-12
(C)m=1,n=-12 (D)m=1,n=12
【解析】选D.因为(x+4)(x-3)=x2+x-12,
而(x+4)(x-3)=x2+mx-n,
所以x2+x-12=x2+mx-n,所以m=1,n=12.【变式备选】若(x+3)(x+n)=x2+mx-15,则m的值为( )
(A)-5 (B)5 (C)-2 (D)2
【解析】选C.因为(x+3)(x+n)=x2+(3+n)x+3n
=x2+mx-15,所以3+n=m,3n=-15,解得n=-5,m=-5+3=-2.3.计算:(a-2b)(2a-b)=_____.
【解析】(a-2b)(2a-b)=2a2-ab-4ab+2b2
=2a2-5ab+2b2.
答案:2a2-5ab+2b24.解方程:8x2-(2x-3)(4x+2)=14.
【解析】8x2-(2x-3)(4x+2)=14,
8x2-(8x2+4x-12x-6)=14,
8x2-8x2-4x+12x+6=14,
8x=8,
x=1.1.下列各式中,计算结果是a2-3a-40的是( )
(A)(a+4)(a-10) (B)(a-4)(a+10)
(C)(a-5)(a+8) (D)(a+5)(a-8)
【解析】选D.(a+4)(a-10)=a2-6a-40;(a-4)(a+10)=a2+6a-40; (a-5)(a+8)=a2+3a-40;(a+5)(a-8)=a2-3a-40.2.长方形一边长3m+2n,另一边比它长m-n,则这个长方形面积是( )
(A)12m2+11mn+2n2 (B)12m2+5mn+2n2
(C)12m2-5mn+2n2 (D)12m2+11mn+n2
【解析】选A.由题意知,另一边的长为3m+2n+m-n=4m+n,
所以这个长方形的面积是(3m+2n)(4m+n)=12m2+11mn+2n2.3.若(x+m)(x+3)整理后结果中不含x的一次项,则m的值为_____.
【解析】因为(x+m)(x+3)=x2+(m+3)x+3m,又因为结果中不含x的一次项,所以m+3=0,解得m=-3.
答案:-34.若(x+6)(x+2)=x(x-3)-21,则x=_____.
【解析】因为(x+6)(x+2)=x2+8x+12,x(x-3)-21=x2-3x-21,所以x2+8x+12=x2-3x-21,所以11x=-33,x=-3.
答案:-35.(2012·安徽中考)计算:(a+3)(a-1)+a(a-2).
【解析】原式=a2-a+3a-3+a2-2a
=2a2-3.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
