:1.7.2 整式的除法(第2课时)(北师大版七年级下册)
文档属性
| 名称 | :1.7.2 整式的除法(第2课时)(北师大版七年级下册) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-15 00:00:00 | ||
图片预览








文档简介
课件22张PPT。第2课时完成下列各题:
(1)因为(____)c=ac+bc,所以(ac+bc)÷c=____.
(2)因为(______)b=ab2+3ab,所以(ab2+3ab)÷b=______.
(3)由于(_____)xy=xy-xy2,所以(xy-xy2)÷xy= _____.a+ba+bab+3aab+3a1-y1-y由以上解题我们不难得出:
(ac+bc)÷c=____=ac÷__+bc÷__.
(ab2+3ab)÷b=______=a2b÷__+3ab÷__.
(xy-xy2)÷xy= _____=xy÷___-xy2÷___.
由此,你能归纳出多项式除以单项式的法则吗?
【归纳】多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.
【点拨】多项式除以单项式的运算是转化为单项式除以单项式来计算的,所以计算中要特别注意每项的符号.a+bab+3ab1-yxyxyccb【预习思考】
多项式中的某一项与除式完全相同时,相除后的结果是多少?
提示:相除的结果是1而不是0. 多项式除以单项式
【例】(9分)计算:
(1)(28a3-14a2+7a)÷7a.
(2)(36x4y3-24x3y2+3x2y2)÷(-6x2y).
(3)[(2x+y)2-y(y+4x)-8x]÷2x.【规范解答】(1)(28a3-14a2+7a)÷7a
=28a3÷7a-14a2÷7a+7a÷7a
=4a2-2a+1.……………………3分
(2)(36x4y3-24x3y2+3x2y2)÷(-6x2y)
=(36x4y3)÷(-6x2y)-(24x3y2)÷(-6x2y)+(3x2y2)÷(-6x2y)
=-6x2y2+4xy- .……………………………………………3分特别提醒:不要漏掉(1)中的最后一项.(3)[(2x+y)2-y(y+4x)-8x]÷2x
=(4x2+4xy+y2-y2-4xy-8x)÷2x
=(4x2-8x)÷2x
=4x2÷2x-8x÷2x
=2x-4.…………………………………………………………3分【互动探究】如何检验多项式除以单项式的结果是否正确?
提示:可以利用乘除是互逆运算,检验计算结果是否正确.【规律总结】
多项式除以单项式中的“三点注意”
1.被除式有几项,则商就有几项,不可丢项.
2.各项系数相除时,应包含前面的符号.当除式的系数为负数时,商式的各项符号与被除多项式各项的符号相反.
3.商的次数小于或等于被除式的次数.【跟踪训练】
1.计算(3x2-x)÷(-x)的正确结果是( )
(A)3x (B)3x-1
(C)-3x+1 (D)-3x-1
【解析】选C.(3x2-x)÷(-x)
=3x2÷(-x)-x÷(-x)=-3x+1.2.5x3y2与一个多项式的积为20x5y2-15x3y4+70(x2y3)2,则这个多项式为( )
(A)4x2-3y2 (B)4x2y-3xy2
(C)4x2-3y2+14xy4 (D)4x2-3y2+7xy3
【解析】选C.依题意得[20x5y2-15x3y4+70(x2y3)2]÷5x3y2 =4x2-3y2+14xy4.【变式备选】
如果(4a2b-3ab2)÷M=-4a+3b,那么单项式M等于( )
(A)ab (B)-ab (C)a (D)-b
【解析】选B.因为(-4a+3b)·(-ab)=4a2b-3ab2,所以M=-ab.3.计算:(-9x2+3x)÷(-3x)=____.
【解析】原式=(-9x2)÷(-3x)+3x÷(-3x)=3x-1.
答案:3x-14.一个长方形的面积为a3-2ab+a,宽为a,则长方形的长为____.
【解析】因为(a3-2ab+a)÷a=a2-2b+1,所以长方形的长为a2-2b+1.
答案:a2-2b+15.计算:(1)(24m3n-16m2n2+mn3)÷(-8m).
(2)[(3x+2y)(3x-2y)-(x+2y)(5x-2y)]÷4x.
【解析】(1)(24m3n-16m2n2+mn3)÷(-8m)
=24m3n÷(-8m)-16m2n2÷(-8m)+mn3÷(-8m)
(2)[(3x+2y)(3x-2y)-(x+2y)(5x-2y)]÷4x
=[(9x2-4y2)-(5x2+8xy-4y2)]÷4x
=(9x2-4y2-5x2-8xy+4y2)÷4x
=(4x2-8xy)÷4x=x-2y.1.计算(8x5-6x3-4x2)÷(-2x)的正确结果是( )
(A)-4x4-3x2+2x (B)-4x4+3x2+2x
(C)4x4+3x2-2x (D)4x4-3x2-2x
【解析】选B.(8x5-6x3-4x2)÷(-2x)
=8x5÷(-2x)-6x3÷(-2x)-4x2÷(-2x)
=-4x4+3x2+2x.2.如果 代数式(28a3-28a2+7a)÷7a的值是( )
(A)6.25 (B)0.25 (C)-2.25 (D)-4
【解析】选B.(28a3-28a2+7a)÷7a=4a2-4a+1=(2a-1)2,把
代入得,原式=0.25. 3.计算:(4m3n3-2m2n- mn)÷(- mn)=____.
【解析】(4m3n3-2m2n- mn)÷(- mn)
=-4m3n3÷ mn+2m2n÷ mn+ mn÷ mn
=-8m2n2+4m+1
答案:-8m2n2+4m+14.若圆柱体的体积是2πa3+3πa2,底面半径为a,则这个圆柱体的高是_____.
【解析】圆柱体的体积=底面积×高,设高为h,则2πa3+3πa2=πa2·h,所以h=(2πa3+3πa2)÷πa2=2a+3.
答案:2a+35.先化简,再求值:[(xy+2)(xy-2)-2(x2y2-2)]÷xy,其中x=1,y=-2.
【解析】[(xy+2)(xy-2)-2(x2y2-2)]÷xy
=[(xy)2-22-2x2y2+4]÷xy
=(x2y2-4-2x2y2+4)÷xy
=(-x2y2)÷xy
=-xy.
当x=1,y=-2 时,原式=-1×(-2)=2.
(1)因为(____)c=ac+bc,所以(ac+bc)÷c=____.
(2)因为(______)b=ab2+3ab,所以(ab2+3ab)÷b=______.
(3)由于(_____)xy=xy-xy2,所以(xy-xy2)÷xy= _____.a+ba+bab+3aab+3a1-y1-y由以上解题我们不难得出:
(ac+bc)÷c=____=ac÷__+bc÷__.
(ab2+3ab)÷b=______=a2b÷__+3ab÷__.
(xy-xy2)÷xy= _____=xy÷___-xy2÷___.
由此,你能归纳出多项式除以单项式的法则吗?
【归纳】多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.
【点拨】多项式除以单项式的运算是转化为单项式除以单项式来计算的,所以计算中要特别注意每项的符号.a+bab+3ab1-yxyxyccb【预习思考】
多项式中的某一项与除式完全相同时,相除后的结果是多少?
提示:相除的结果是1而不是0. 多项式除以单项式
【例】(9分)计算:
(1)(28a3-14a2+7a)÷7a.
(2)(36x4y3-24x3y2+3x2y2)÷(-6x2y).
(3)[(2x+y)2-y(y+4x)-8x]÷2x.【规范解答】(1)(28a3-14a2+7a)÷7a
=28a3÷7a-14a2÷7a+7a÷7a
=4a2-2a+1.……………………3分
(2)(36x4y3-24x3y2+3x2y2)÷(-6x2y)
=(36x4y3)÷(-6x2y)-(24x3y2)÷(-6x2y)+(3x2y2)÷(-6x2y)
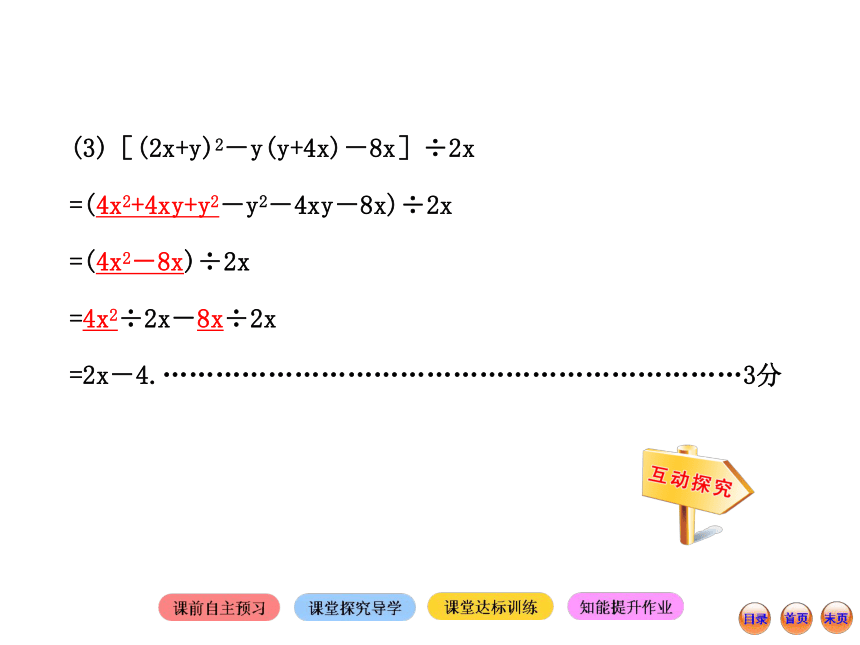
=-6x2y2+4xy- .……………………………………………3分特别提醒:不要漏掉(1)中的最后一项.(3)[(2x+y)2-y(y+4x)-8x]÷2x
=(4x2+4xy+y2-y2-4xy-8x)÷2x
=(4x2-8x)÷2x
=4x2÷2x-8x÷2x
=2x-4.…………………………………………………………3分【互动探究】如何检验多项式除以单项式的结果是否正确?
提示:可以利用乘除是互逆运算,检验计算结果是否正确.【规律总结】
多项式除以单项式中的“三点注意”
1.被除式有几项,则商就有几项,不可丢项.
2.各项系数相除时,应包含前面的符号.当除式的系数为负数时,商式的各项符号与被除多项式各项的符号相反.
3.商的次数小于或等于被除式的次数.【跟踪训练】
1.计算(3x2-x)÷(-x)的正确结果是( )
(A)3x (B)3x-1
(C)-3x+1 (D)-3x-1
【解析】选C.(3x2-x)÷(-x)
=3x2÷(-x)-x÷(-x)=-3x+1.2.5x3y2与一个多项式的积为20x5y2-15x3y4+70(x2y3)2,则这个多项式为( )
(A)4x2-3y2 (B)4x2y-3xy2
(C)4x2-3y2+14xy4 (D)4x2-3y2+7xy3
【解析】选C.依题意得[20x5y2-15x3y4+70(x2y3)2]÷5x3y2 =4x2-3y2+14xy4.【变式备选】
如果(4a2b-3ab2)÷M=-4a+3b,那么单项式M等于( )
(A)ab (B)-ab (C)a (D)-b
【解析】选B.因为(-4a+3b)·(-ab)=4a2b-3ab2,所以M=-ab.3.计算:(-9x2+3x)÷(-3x)=____.
【解析】原式=(-9x2)÷(-3x)+3x÷(-3x)=3x-1.
答案:3x-14.一个长方形的面积为a3-2ab+a,宽为a,则长方形的长为____.
【解析】因为(a3-2ab+a)÷a=a2-2b+1,所以长方形的长为a2-2b+1.
答案:a2-2b+15.计算:(1)(24m3n-16m2n2+mn3)÷(-8m).
(2)[(3x+2y)(3x-2y)-(x+2y)(5x-2y)]÷4x.
【解析】(1)(24m3n-16m2n2+mn3)÷(-8m)
=24m3n÷(-8m)-16m2n2÷(-8m)+mn3÷(-8m)
(2)[(3x+2y)(3x-2y)-(x+2y)(5x-2y)]÷4x
=[(9x2-4y2)-(5x2+8xy-4y2)]÷4x
=(9x2-4y2-5x2-8xy+4y2)÷4x
=(4x2-8xy)÷4x=x-2y.1.计算(8x5-6x3-4x2)÷(-2x)的正确结果是( )
(A)-4x4-3x2+2x (B)-4x4+3x2+2x
(C)4x4+3x2-2x (D)4x4-3x2-2x
【解析】选B.(8x5-6x3-4x2)÷(-2x)
=8x5÷(-2x)-6x3÷(-2x)-4x2÷(-2x)
=-4x4+3x2+2x.2.如果 代数式(28a3-28a2+7a)÷7a的值是( )
(A)6.25 (B)0.25 (C)-2.25 (D)-4
【解析】选B.(28a3-28a2+7a)÷7a=4a2-4a+1=(2a-1)2,把
代入得,原式=0.25. 3.计算:(4m3n3-2m2n- mn)÷(- mn)=____.
【解析】(4m3n3-2m2n- mn)÷(- mn)
=-4m3n3÷ mn+2m2n÷ mn+ mn÷ mn
=-8m2n2+4m+1
答案:-8m2n2+4m+14.若圆柱体的体积是2πa3+3πa2,底面半径为a,则这个圆柱体的高是_____.
【解析】圆柱体的体积=底面积×高,设高为h,则2πa3+3πa2=πa2·h,所以h=(2πa3+3πa2)÷πa2=2a+3.
答案:2a+35.先化简,再求值:[(xy+2)(xy-2)-2(x2y2-2)]÷xy,其中x=1,y=-2.
【解析】[(xy+2)(xy-2)-2(x2y2-2)]÷xy
=[(xy)2-22-2x2y2+4]÷xy
=(x2y2-4-2x2y2+4)÷xy
=(-x2y2)÷xy
=-xy.
当x=1,y=-2 时,原式=-1×(-2)=2.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
