浙江省宁波市2023年中考数学押题密卷(含解析)
文档属性
| 名称 | 浙江省宁波市2023年中考数学押题密卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-09 15:04:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江省宁波市2023年中考数学押题密卷
一.选择题(共10小题,满分40分,每小题4分)
1.﹣2023的倒数为( )
A.﹣2023 B. C. D.2023
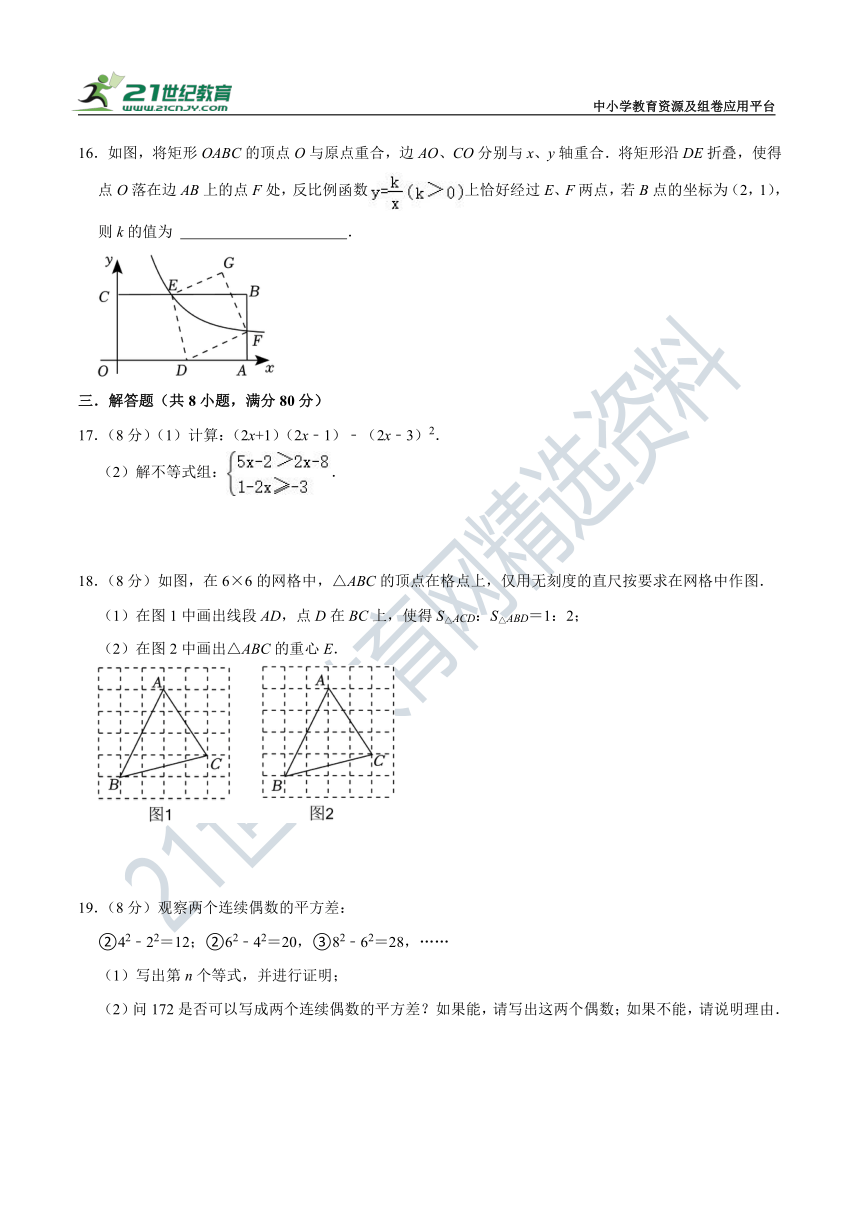
2.下列计算正确的是( )
A.a3+a3=2a6 B.a3×a3=a6 C.a6÷a3=a2 D.(3a)3=9a3
3.我国研究人员利用中国天眼对致密星系群“斯蒂芬五重星系”及周围天区的氢原子气体进行成像观测,发现了1个尺度大约为200万光年的巨大原子气体系统,尺度比银河系大20倍.长度单位光年是指光在真空中传播一年所经过的距离,大约为9460700000000千米,将数9460700000000用科学记数法表示为( )
A.9.4607×1011 B.9.4607×1012
C.94607×108 D.0.94607×1013
4.如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
5.某学习小组9名学生参加“生活中的数学知识竞赛”,他们的得分情况如表:
人数(人) 1 3 4 1
分数(分) 80 85 90 95
那么这9名学生所得分数的众数和中位数分别是( )
A.90,90 B.90,85 C.90,87.5 D.85,85
6.有5张卡片,正面分别写着“冰墩墩”、“雪容融”、“琮琮”、“莲莲”、“辰辰”,其余都相同,正面朝下放置.小军从中任取一张恰为杭州亚运会吉祥物的概率为( )
(注:“冰墩墩”是北京冬奥会的吉祥物,“雪容融”为北京冬残奥会吉祥物,“琮琮”、“莲莲”、“辰辰”都是杭州亚运会的吉祥物)
A. B. C. D.
7.如图,在△ABC中,AB=AC,∠A=36°.以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于点N.接着分别以点M,N为圆心,大于长为半径作圆弧,两弧交于点H.作射线BH,交AC于点D.再以点D为圆心,DC长为半径作圆弧,交BC于点E,连结DE.则下列说法错误的是( )
A.AD=BD B.∠BDC=∠BCD C. D.△BED∽△BDA
8.我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:现在有数人一起去买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问共有多少人,物品的价格是多少钱?若设人数共有x人,物品的价格为y钱,可列方程组为( )
A. B.
C. D.
9.如图,已知圆锥侧面展开图的扇形面积为65πcm2,扇形的弧长为10πcm,则圆锥的高是( )
A.5cm B.10cm C.12cm D.13cm
10.如图,一次函数y1=kx+b(k≠0)与反比例函数的图象相交于A(1,2),B(﹣2,a)两点,则不等式kx+b﹣<0的解是( )
A.x<﹣2 B.x<﹣2或0<x<1
C.﹣2<x<0或x>1 D.x<1
二.填空题(共6小题,满分30分,每小题5分)
11.= .
12.分解因式:x2﹣4= .
13.如图,以AB为直径的⊙O与BC相切于点B,交AC于点D.若∠CBD=30°,则∠CAB的度数为 .
14.定义一种新运算:对于任意的非零实数a,b,a b=.若(x﹣1) (x+1)=,则x的值为 .
15.如图,二次函数y=ax2+bx+c(a≠0)图象经过点A(﹣1,﹣2),对称轴为直线x=1,则9a+3b+c的值是 .
16.如图,将矩形OABC的顶点O与原点重合,边AO、CO分别与x、y轴重合.将矩形沿DE折叠,使得点O落在边AB上的点F处,反比例函数上恰好经过E、F两点,若B点的坐标为(2,1),则k的值为 .
三.解答题(共8小题,满分80分)
17.(8分)(1)计算:(2x+1)(2x﹣1)﹣(2x﹣3)2.
(2)解不等式组:.
18.(8分)如图,在6×6的网格中,△ABC的顶点在格点上,仅用无刻度的直尺按要求在网格中作图.
(1)在图1中画出线段AD,点D在BC上,使得S△ACD:S△ABD=1:2;
(2)在图2中画出△ABC的重心E.
19.(8分)观察两个连续偶数的平方差:
②42﹣22=12;②62﹣42=20,③82﹣62=28,……
(1)写出第n个等式,并进行证明;
(2)问172是否可以写成两个连续偶数的平方差?如果能,请写出这两个偶数;如果不能,请说明理由.
20.(8分)新能源车是当下热点,某品牌新能源汽车去年8~12月五个月的销售总量为106万台,图1表示该品牌新能源汽车8~12月各月的销量,图2表示该品牌新能源汽车8~12月各月和上个月的环比增长率,请解答下列问题:
(1)请你根据信息将统计图1补充完整;
(2)增长率最大的是哪个月,增长了多少万台;
(3)小明观察图2后认为,从十月份开始该品牌新能源汽车的销量逐渐降低.他的说法正确吗?请说明理由.
21.(10分)我市的花果山景区大圣湖畔屹立着一座古塔——阿育王塔,是苏北地区现存最高和最古老的宝塔.小明与小亮要测量阿育王塔的高度,如图所示,小明在点A处测得阿育王塔最高点C的仰角∠CAE=45°,再沿正对阿育王塔方向前进至B处测得最高点C的仰角∠CBE=53°,AB=10m;小亮在点G处竖立标杆FG,小亮的所在位置点D、标杆顶F、最高点C在一条直线上,FG=1.5m,GD=2m.
(1)求阿育王塔的高度CE;
(2)求小亮与阿育王塔之间的距离ED.
(注:结果精确到0.01m,参考数据:sin53°≈0.799,cos53°≈0.602,tan53°≈1.327)
22.(12分)乌馒头是江北慈城地方特色点心,用麦粉发酵,再掺以白糖黄糖,蒸制而成.因其用黄糖,颜色暗黄,所以称之谓“乌馒头”.某商店销售乌馒头,通过分析销售情况发现,乌馒头的日销售量y(盒)是销售单价x(元/盒)的一次函数,销售单价、日销售量的部分对应值如下表,已知销售单价不低于成本价且不高于20元,每天销售乌馒头的固定损耗为20元,且销售单价为18元/盒时,日销售纯利润为1180元.
销售单价x(元/盒) 15 13
日销售量y(盒) 500 700
(1)求乌馒头的日销售量y(盒)与销售单价x(元/盒)的函数表达式;
(2)“端午乌馒重阳粽”是慈城的习俗.端午节期间,商店决定采用降价促销的方式回馈顾客.在顾客获得最大实惠的前提下,当乌馒头每盒降价多少元时,商店日销售纯利润为1480元?
(3)当销售单价定为多少时,日销售纯利润最大,并求此日销售最大纯利润.
23.(12分)【基础巩固】
(1)如图1,在△ABC中,D为BC上一点,连结AD,E为AD上一点,连结CE,若∠BAD=∠ACE,CD=CE,求证:△ABD∽△CAE.
【尝试应用】
(2)如图2,在平行四边形ABCD中,对角线AC、BD交于点O,E为OC上一点,连结BE,∠CBE=∠DCO,BE=DO,若BD=12,OE=5,求AC的长.
【拓展提升】
(3)如图3,在菱形ABCD中,对角线AC、BD交于点O,E为BC中点,F为DC上一点,连结OE、AF,∠AEO=∠CAF,若,AC=6,求菱形ABCD的边长.
24.(14分)如图1,AC,BD是⊙O的两条弦,且BD⊥AC于点E.
(1)若AE=BE,求证:DE=CE.
(2)如图2,连结AB,BC,CD,若CA=CD,
①判断∠ACB与∠ACD具有怎样的数量关系,并说明理由.
②在BD上存在点F,满足BF=2AB,M是的中点,连结MF.若,MF=2,求⊙O的半径.
浙江省宁波市2023年中考数学押题密卷
试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.﹣2023的倒数为( )
A.﹣2023 B. C. D.2023
【分析】乘积是1的两数互为倒数,由此即可得到答案.
【解答】解:﹣2023的倒数为﹣.
故选:C.
2.下列计算正确的是( )
A.a3+a3=2a6 B.a3×a3=a6 C.a6÷a3=a2 D.(3a)3=9a3
【分析】利用合并同类项的法则,同底数幂的除法的法则,同底数幂的乘法的法则,积的乘方的法则对各项进行运算即可.
【解答】解:A、a3+a3=2a3,故A不符合题意;
B、a3×a3=a6,故B符合题意;
C、a6÷a3=a3,故C不符合题意;
D、(3a)3=27a3,故D不符合题意;
故选:B.
3.我国研究人员利用中国天眼对致密星系群“斯蒂芬五重星系”及周围天区的氢原子气体进行成像观测,发现了1个尺度大约为200万光年的巨大原子气体系统,尺度比银河系大20倍.长度单位光年是指光在真空中传播一年所经过的距离,大约为9460700000000千米,将数9460700000000用科学记数法表示为( )
A.9.4607×1011 B.9.4607×1012
C.94607×108 D.0.94607×1013
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:9460700000000=9.4607×1012.
故选:B.
4.如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
【分析】根据主视图是从物体的正面看得到的视图解答即可.
【解答】解:从正面看,共有两列,从左到右小正方形的个数分别为3、1.
故选:A.
5.某学习小组9名学生参加“生活中的数学知识竞赛”,他们的得分情况如表:
人数(人) 1 3 4 1
分数(分) 80 85 90 95
那么这9名学生所得分数的众数和中位数分别是( )
A.90,90 B.90,85 C.90,87.5 D.85,85
【分析】众数是一组数据中出现次数最多的数据;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;可得答案.
【解答】解:在这一组数据中90是出现次数最多的,故众数是90;
排序后处于中间位置的那个数是90,那么由中位数的定义可知,这组数据的中位数是90.
故选:A.
6.有5张卡片,正面分别写着“冰墩墩”、“雪容融”、“琮琮”、“莲莲”、“辰辰”,其余都相同,正面朝下放置.小军从中任取一张恰为杭州亚运会吉祥物的概率为( )
(注:“冰墩墩”是北京冬奥会的吉祥物,“雪容融”为北京冬残奥会吉祥物,“琮琮”、“莲莲”、“辰辰”都是杭州亚运会的吉祥物)
A. B. C. D.
【分析】直接根据概率公式求解.
【解答】解:∵5张卡片上有3张为杭州亚运会吉祥物,
∴小军从中任取一张恰为杭州亚运会吉祥物的概率为.
故选:C.
7.如图,在△ABC中,AB=AC,∠A=36°.以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于点N.接着分别以点M,N为圆心,大于长为半径作圆弧,两弧交于点H.作射线BH,交AC于点D.再以点D为圆心,DC长为半径作圆弧,交BC于点E,连结DE.则下列说法错误的是( )
A.AD=BD B.∠BDC=∠BCD C. D.△BED∽△BDA
【分析】由作图得BD平分∠ABC,DE=DC,由AB=AC,∠A=36°,得∠ABC=∠ACB=72°,则∠ABD=∠CBD=36°=∠A,所以AD=BD,可判断A正确;因为∠BDC=∠ABD+∠A=72°,∠BCD=72°,所以∠BDC=∠BCD,可判断B正确;因为∠DEC=∠DCE=72°,所以∠EDB=∠DEC﹣∠CBD=36°,则∠EDB=∠CBD,所以BE=DE=DC,由∠DBE=∠ABD=36°,∠EDB=∠A=36°,得△BED∽△BDA,可判断D正确;由=,得=,则AD2=DC AC,可证明AD=BE≠BE,可判断C错误,于是得到问题的答案.
【解答】解:由作图得BD平分∠ABC,DE=DC,
∵AB=AC,∠A=36°,
∴∠ABC=∠ACB==72°,
∴∠ABD=∠CBD=∠ABC=×72°=36°,
∴∠ABD=∠A,
∴AD=BD,
故A正确;
∵∠BDC=∠ABD+∠A=36°+36°=72°,∠BCD=72°,
∴∠BDC=∠BCD,
故B正确;
∵DE=DC,
∴∠DEC=∠DCE=72°,
∴∠EDB=∠DEC﹣∠CBD=72°﹣36°=36°,
∴∠EDB=∠CBD,
∴BE=DE=DC,
∵∠DBE=∠ABD=36°,∠EDB=∠A=36°,
∴△BED∽△BDA,
故D正确;
∴=,
∴=,
∴AD2=DC AC,
设AD=x,BE=DC=m,则AC=x+m,
∴x2=m(x+m),
解关于x的方程得x1=m,x2=m(不符合题意,舍去),
∴AD=BE≠BE,
故C错误,
故选:C.
8.我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:现在有数人一起去买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问共有多少人,物品的价格是多少钱?若设人数共有x人,物品的价格为y钱,可列方程组为( )
A. B.
C. D.
【分析】根据题意可以找出题目中的等量关系,列出相应的方程组,从而可以解答本题.
【解答】解:由题意可得,.
故选:D.
9.如图,已知圆锥侧面展开图的扇形面积为65πcm2,扇形的弧长为10πcm,则圆锥的高是( )
A.5cm B.10cm C.12cm D.13cm
【分析】圆锥的侧面积=×弧长×母线长,把相应数值代入即可求解可得圆锥的母线长,然后可以利用勾股定理求得圆锥的高.
【解答】解:设母线长为R,由题意得:65π=×10π×R,解得R=13cm.
设圆锥的底面半径为r,则10π=2πr,
解得:r=5,
故圆锥的高为:=12
故选:C.
10.如图,一次函数y1=kx+b(k≠0)与反比例函数的图象相交于A(1,2),B(﹣2,a)两点,则不等式kx+b﹣<0的解是( )
A.x<﹣2 B.x<﹣2或0<x<1
C.﹣2<x<0或x>1 D.x<1
【分析】一次函数y1=kx+b落在与反比例函数的图象下方的部分对应的自变量的取值范围即为所求.
【解答】解:∵一次函数y1=kx+b(k≠0)与反比例函数的图象相交于A(1,2),B(﹣2,a)两点,
∴不等式kx+b﹣<0的解集是x<﹣2或0<x<1.
故选:B.
二.填空题(共6小题,满分30分,每小题5分)
11.= 2 .
【分析】利用算术平方根定义计算即可求出值.
【解答】解:∵22=4,
∴4的算术平方根是2,即=2.
故答案为:2.
12.分解因式:x2﹣4= (x+2)(x﹣2) .
【分析】直接利用平方差公式进行因式分解即可.
【解答】解:x2﹣4=(x+2)(x﹣2).
故答案为:(x+2)(x﹣2).
13.如图,以AB为直径的⊙O与BC相切于点B,交AC于点D.若∠CBD=30°,则∠CAB的度数为 30° .
【分析】利用圆的切线的性质定理∠CBD+∠ABD=90°,利用圆周角定理得到∠CAB+∠ABD=90°,利用同角的余角相等即可得出结论.
【解答】解:∵以AB为直径的⊙O与BC相切于点B,
∴AB⊥BC,
∴∠ABC=90°,
∴∠CBD+∠ABD=90°.
∵AB为直径,
∴∠ADB=90°,
∴∠CAB+∠ABD=90°,
∴∠CAB=∠CBD=30°.
故答案为:30°.
14.定义一种新运算:对于任意的非零实数a,b,a b=.若(x﹣1) (x+1)=,则x的值为 x=2 .
【分析】根据题干的新定义,得到.再解这分式方程,进而求得x.
【解答】解:由题意得,.
去分母,得x+1+x﹣1=3x﹣2.
移项,得x+x﹣3x=﹣2+1﹣1.
合并同类项,得﹣x=﹣2.
x的系数化为1,得x=2.
检验:当x=2,(x+1)(x﹣1)≠0.
∴该分式方程的解为x=2.
故答案为:x=2.
15.如图,二次函数y=ax2+bx+c(a≠0)图象经过点A(﹣1,﹣2),对称轴为直线x=1,则9a+3b+c的值是 ﹣2 .
【分析】根据抛物线的轴对称性质得到:当x=3与当x=﹣1时,所对应的y值相等,据此解答.
【解答】解:∵二次函数y=ax2+bx+c(a≠0)图象经过点A(﹣1,﹣2),对称轴为直线x=1,
∴点A(﹣1,﹣2)关于直线x=1对称的点的坐标为(3,﹣2).
∴当x=3时,y=﹣2,
即9a+3b+c=﹣2.
故答案为:﹣2.
16.如图,将矩形OABC的顶点O与原点重合,边AO、CO分别与x、y轴重合.将矩形沿DE折叠,使得点O落在边AB上的点F处,反比例函数上恰好经过E、F两点,若B点的坐标为(2,1),则k的值为 10﹣2 .
【分析】连结OF,过E作EH⊥OA于H,由B点坐标为(2,1),即可得出E点的坐标为(k,1),F点的坐标为,证得△EHD∽△OAF,得到,求得,进而求得,,由折叠可得,利用勾股定理得到关于k的方程,解方程即可求得k的值.
【解答】解:连结OF,过E作EH⊥OA于H.
∵B点坐标为(2,1),
∴E点的纵坐标为1,F点的横坐标为2,
∵反比例函数上恰好经过E、F两点,
∴E点的坐标为(k,1),F点的坐标为,
∵∠EDH+∠AOF=∠EDH+∠HED=90°,
∴∠AOF=∠HED,
又∠EHD=∠OAF=90°,
∴△EHD∽△OAF,
∴,即,
∴,
∴,,
由折叠可得,
在Rt△DAF中,由勾股定理可得,
解得,(舍).
∴k的值为10﹣2.
故答案为:10﹣2.
三.解答题(共8小题,满分80分)
17.(8分)(1)计算:(2x+1)(2x﹣1)﹣(2x﹣3)2.
(2)解不等式组:.
【分析】(1)先用平方差公式、完全平方公式,再合并同类项;
(2)先解不等式组中的各不等式,再确定不等式组的解集.
【解答】解:(1)原式=4x2﹣1﹣(4x2﹣12x+9)
=4x2﹣1﹣4x2+12x﹣9
=12x﹣10;
(2),
解①得x>﹣2,
解②得x≤2.
∴不等式组的解集为﹣2<x≤2.
18.(8分)如图,在6×6的网格中,△ABC的顶点在格点上,仅用无刻度的直尺按要求在网格中作图.
(1)在图1中画出线段AD,点D在BC上,使得S△ACD:S△ABD=1:2;
(2)在图2中画出△ABC的重心E.
【分析】(1)取格点P,Q连接PQ交BC于点D,连接AD即可;
(2)作直线BM,CN交于点E,点E即为所求.
【解答】解:(1)如图1中,点D即为所求;
(2)如图2中,点E即为所求.
19.(8分)观察两个连续偶数的平方差:
②42﹣22=12;②62﹣42=20,③82﹣62=28,……
(1)写出第n个等式,并进行证明;
(2)问172是否可以写成两个连续偶数的平方差?如果能,请写出这两个偶数;如果不能,请说明理由.
【分析】(1)根据给定的例子可得第n个等式是:(2n+2)2﹣(2n)2=4(2n+1),根据平方差公式的逆运算证明即可;
(2)当8n+4=172时,解得n=21,即可确定答案.
【解答】解:(1)第n个等式是:(2n+2)2﹣(2n)2=4(2n+1),证明如下:
∵(2n+2)2﹣(2n)2
=(2n+2+2n)(2n+2﹣2n)
=2(4n+2)
=4(2n+1),
∴(2n+2)2﹣(2n)2=4(2n+1).
(2)172可以写成两个连续偶数的平方差,这两个偶数是42和44,理由如下:
当8n+4=172时,解得n=21,
∴2n=2×21=42,2n+2=42+2=44,
∴两个偶数分别为42和44.
20.(8分)新能源车是当下热点,某品牌新能源汽车去年8~12月五个月的销售总量为106万台,图1表示该品牌新能源汽车8~12月各月的销量,图2表示该品牌新能源汽车8~12月各月和上个月的环比增长率,请解答下列问题:
(1)请你根据信息将统计图1补充完整;
(2)增长率最大的是哪个月,增长了多少万台;
(3)小明观察图2后认为,从十月份开始该品牌新能源汽车的销量逐渐降低.他的说法正确吗?请说明理由.
【分析】(1)用销售总量减去其他四个月的销售量可得9月份的销售量,进而补全条形统计图;
(2)结合统计图数据列式计算即可;
(3)根据增长率的定义解答即可.
【解答】解:(1)由题意可知,9月份销量为106﹣(17.5+22+23+23.5)=20(万台).
所补作图形如图所示:
(2)由题意可知,9月增长率最高为14.3%,增长了20﹣17.5=2.5(万台);
(3)小明的说法是错误的,理由如下:
因为10~12月份只是增长率降低,但是增长率仍为正,说明销量仍在增加(答案不唯一).
21.(10分)我市的花果山景区大圣湖畔屹立着一座古塔——阿育王塔,是苏北地区现存最高和最古老的宝塔.小明与小亮要测量阿育王塔的高度,如图所示,小明在点A处测得阿育王塔最高点C的仰角∠CAE=45°,再沿正对阿育王塔方向前进至B处测得最高点C的仰角∠CBE=53°,AB=10m;小亮在点G处竖立标杆FG,小亮的所在位置点D、标杆顶F、最高点C在一条直线上,FG=1.5m,GD=2m.
(1)求阿育王塔的高度CE;
(2)求小亮与阿育王塔之间的距离ED.
(注:结果精确到0.01m,参考数据:sin53°≈0.799,cos53°≈0.602,tan53°≈1.327)
【分析】(1)由∠CAE=45°,AB=10m,可得BE=AE﹣10=CE﹣10,在Rt△CEB中,可得tan∠CBE=tan53°==,即可解得阿育王塔的高度CE约为40.58m;
(2)由△FGD∽△CED,可得=,可解得小亮与阿育王塔之间的距离ED是54.11m.
【解答】解:(1)在Rt△CAE中,
∵∠CAE=45°,
∴CE=AE,
∵AB=10m,
∴BE=AE﹣10=CE﹣10,
在Rt△CEB中,
tan∠CBE=tan53°==,
∴1.327≈,
解得CE≈40.58(m);
答:阿育王塔的高度CE约为40.58m;
(2)由题意知:∠CED=90°=∠FGD,∠FDG=∠CDE,
∴△FGD∽△CED,
∴=,即=,
解得ED≈54.11(m),
答:小亮与阿育王塔之间的距离ED约是54.11m.
22.(12分)乌馒头是江北慈城地方特色点心,用麦粉发酵,再掺以白糖黄糖,蒸制而成.因其用黄糖,颜色暗黄,所以称之谓“乌馒头”.某商店销售乌馒头,通过分析销售情况发现,乌馒头的日销售量y(盒)是销售单价x(元/盒)的一次函数,销售单价、日销售量的部分对应值如下表,已知销售单价不低于成本价且不高于20元,每天销售乌馒头的固定损耗为20元,且销售单价为18元/盒时,日销售纯利润为1180元.
销售单价x(元/盒) 15 13
日销售量y(盒) 500 700
(1)求乌馒头的日销售量y(盒)与销售单价x(元/盒)的函数表达式;
(2)“端午乌馒重阳粽”是慈城的习俗.端午节期间,商店决定采用降价促销的方式回馈顾客.在顾客获得最大实惠的前提下,当乌馒头每盒降价多少元时,商店日销售纯利润为1480元?
(3)当销售单价定为多少时,日销售纯利润最大,并求此日销售最大纯利润.
【分析】(1)设y=kx+b,根据表格即可求解;
(2)根据:销售量×单件利润﹣损耗费用=销售总利润,列出方程即可求解;
(3)设日销售纯利润为w元,根据:销售量×单件利润﹣损耗费用=销售总利润,列出函数关系式,并在12≤x≤20求最值即可.
【解答】解:(1)设y=kx+b,由题意得
,
解得,
∴y=﹣100x+2000.
(2)当x=18时,y=200,
即销售200盒的纯利润为1180元,
∴成本价为:18﹣(1180+20)÷200=12(元),
(﹣100x+2000)(x﹣12)=1480+20,
解得:x1=17(舍),x2=15,
18﹣15=3(元).
答:当乌馒头每盒降价3元时,商店每天获利为1480元.
(3)设日销售纯利润为w元,由题意得
w=(﹣100x+2000)(x﹣12)﹣20
=﹣100x2+3200x﹣24020
=﹣100(x﹣16)2+1580,
∵﹣100<0,12≤x≤20,
∴当x=16时,w有最大值1580元,
答:当销售单价定为16元/盒时,日销售纯利润最大,最大纯利润为1580元.
23.(12分)【基础巩固】
(1)如图1,在△ABC中,D为BC上一点,连结AD,E为AD上一点,连结CE,若∠BAD=∠ACE,CD=CE,求证:△ABD∽△CAE.
【尝试应用】
(2)如图2,在平行四边形ABCD中,对角线AC、BD交于点O,E为OC上一点,连结BE,∠CBE=∠DCO,BE=DO,若BD=12,OE=5,求AC的长.
【拓展提升】
(3)如图3,在菱形ABCD中,对角线AC、BD交于点O,E为BC中点,F为DC上一点,连结OE、AF,∠AEO=∠CAF,若,AC=6,求菱形ABCD的边长.
【分析】(1)可证得∠CDE=∠CED,从而∠ADB=∠CEA,进一步得出结论;
(2)可证得∠BEO=∠BOE,从而得出∠BEC=∠COD,进而得出△BEC∽△COD,从而,设OC=x,则CE=OC﹣OE=x﹣5,从而得出,从而求得x的值,进一步得出结果;
(3)延长AG,BC,交于点G,可得出△CGF∽△DAF,从而,进而表示出CG,可证得△AOE∽△GCA,从而,进而求得t的值,进一步得出结果.
【解答】(1)证明:∵CD=CE,
∴∠CDE=∠CED,
∴180°﹣∠CDE=180°﹣∠CED,
∴∠ADB=∠CEA,
∵∠BAD=∠ACE,
∴△ABD∽△CAE.
(2)解:∵四边形ABCD是平行四边形,
∴,
∴BE=DO=BO=6.
∴∠BEO=∠BOE,
∴180°﹣∠BEO=180°﹣∠BOE,
∴∠BEC=∠COD.
∵∠CBE=∠DCO,
∴△BEC∽△COD,
∴,
设OC=x,则CE=OC﹣OE=x﹣5,
∴,
∴x1=9,x2=﹣4(舍去),
∴OC=9,
∴AC=2OC=18;
(3)解:如图,
延长AG,BC,交于点G.
∵,
∴设DF=5t,FC=3t,则CD=8t,
∵四边形ABCD是菱形,
∴AB=AD=BC=CD=8t,AD∥BC,,AC⊥BD,
∴△CGF∽△DAF,
∴,
即,
∴.
在Rt△BOC中,
∵E为BC的中点,
∴OE=CE=BC=4t.
∴∠COE=∠ACE,
∴∠AOE=∠ACG,
∵∠AEO=∠CAF,
∴△AOE∽△GCA,
∴,
即,
∴t1=,t2=﹣(舍去),
∴,
即菱形ABCD的边长为.
24.(14分)如图1,AC,BD是⊙O的两条弦,且BD⊥AC于点E.
(1)若AE=BE,求证:DE=CE.
(2)如图2,连结AB,BC,CD,若CA=CD,
①判断∠ACB与∠ACD具有怎样的数量关系,并说明理由.
②在BD上存在点F,满足BF=2AB,M是的中点,连结MF.若,MF=2,求⊙O的半径.
【分析】(1)连接AD,BC.证明△ADE∽△BCE,由相似三角形的性质得出,进一步得出结论;
(2)①作OF⊥AC于F,作OG⊥CD于G,可推出OC平分∠ACD,可推出∠A+∠ACH=90°,∠A+∠ADE=90°,进而∠ADE=∠ACH,进一步得出结果;
②连接CM,交BD于H,连接AM,作AG∥MF,交BD于G,可推出△CEH∽△CAM,四边形AGFM是平行四边形,从而,AG=MF=2,FG=AM=2,进而得出FG的长,可推出EH=EB,设BE=x,则EG=﹣x,由AE2=AG2﹣EG2=AB2﹣BE2,列出22﹣(2﹣x)2=(2)2﹣x2,从而求得x的值,则求出BE及AE的长,由比例线段可求出CE,进一步得出结果.
【解答】(1)证明:如图1,
连接AD,BC,
∵,,
∴∠D=∠C,∠A=∠B,
∴△ADE∽△BCE,
∴,
∵AE=BE,
∴DE=CE;
(2)解:①如图2,
∠ACB=∠ACD,理由如下:
作OF⊥AC于F,作OG⊥CD于G,
CF=AC,CG=CD,
∵AC=CD,
∴CF=CG,
∴∠COF=∠COG,
∴∠ACO=∠DCO,
∴CH⊥AD,
∴∠AHC=90°,
∴∠A+∠ACH=90°,
∵BD⊥AC,
∴∠AED=90°,
∴∠A+∠ADE=90°,
∴∠ADE=∠ACH,
∵∠ACB=∠ADE,
∴∠ACB=∠ACH=∠ACD;
②如图3,
连接CM,交BD于H,连接AM,作AG∥MF,交BD于G,
∴∠MAC=90°,
∵BD⊥AC,
∴∠DEC=90°,
∴∠DEC=∠MAC,
∴AM∥BD,
∴△CEH∽△CAM,四边形AGFM是平行四边形,
∴,AG=MF=2,FG=AM,
由①得,
∠ACB=∠ACM,
∴=,
∴AM=AB=2,
∴FG=2,
∴BG=BF﹣FG=2,
∵∠CEB=∠CEH=90°,
∴∠CHE=∠CBE,
∴CH=CB,
∴EH=EB,
设BE=x,则EG=2﹣x,
由AE2=AG2﹣EG2=AB2﹣BE2,
∴22﹣(2﹣x)2=(2)2﹣x2,
∴x=,
∴EH=BE=,
∴AE=(2)2﹣()2,
∴AE=,
∴,
∴CE=,
∴AC=CE+AE=2,
∴CM===8,
∴圆的半径为4.
浙江省宁波市2023年中考数学押题密卷
一.选择题(共10小题,满分40分,每小题4分)
1.﹣2023的倒数为( )
A.﹣2023 B. C. D.2023
2.下列计算正确的是( )
A.a3+a3=2a6 B.a3×a3=a6 C.a6÷a3=a2 D.(3a)3=9a3
3.我国研究人员利用中国天眼对致密星系群“斯蒂芬五重星系”及周围天区的氢原子气体进行成像观测,发现了1个尺度大约为200万光年的巨大原子气体系统,尺度比银河系大20倍.长度单位光年是指光在真空中传播一年所经过的距离,大约为9460700000000千米,将数9460700000000用科学记数法表示为( )
A.9.4607×1011 B.9.4607×1012
C.94607×108 D.0.94607×1013
4.如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
5.某学习小组9名学生参加“生活中的数学知识竞赛”,他们的得分情况如表:
人数(人) 1 3 4 1
分数(分) 80 85 90 95
那么这9名学生所得分数的众数和中位数分别是( )
A.90,90 B.90,85 C.90,87.5 D.85,85
6.有5张卡片,正面分别写着“冰墩墩”、“雪容融”、“琮琮”、“莲莲”、“辰辰”,其余都相同,正面朝下放置.小军从中任取一张恰为杭州亚运会吉祥物的概率为( )
(注:“冰墩墩”是北京冬奥会的吉祥物,“雪容融”为北京冬残奥会吉祥物,“琮琮”、“莲莲”、“辰辰”都是杭州亚运会的吉祥物)
A. B. C. D.
7.如图,在△ABC中,AB=AC,∠A=36°.以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于点N.接着分别以点M,N为圆心,大于长为半径作圆弧,两弧交于点H.作射线BH,交AC于点D.再以点D为圆心,DC长为半径作圆弧,交BC于点E,连结DE.则下列说法错误的是( )
A.AD=BD B.∠BDC=∠BCD C. D.△BED∽△BDA
8.我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:现在有数人一起去买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问共有多少人,物品的价格是多少钱?若设人数共有x人,物品的价格为y钱,可列方程组为( )
A. B.
C. D.
9.如图,已知圆锥侧面展开图的扇形面积为65πcm2,扇形的弧长为10πcm,则圆锥的高是( )
A.5cm B.10cm C.12cm D.13cm
10.如图,一次函数y1=kx+b(k≠0)与反比例函数的图象相交于A(1,2),B(﹣2,a)两点,则不等式kx+b﹣<0的解是( )
A.x<﹣2 B.x<﹣2或0<x<1
C.﹣2<x<0或x>1 D.x<1
二.填空题(共6小题,满分30分,每小题5分)
11.= .
12.分解因式:x2﹣4= .
13.如图,以AB为直径的⊙O与BC相切于点B,交AC于点D.若∠CBD=30°,则∠CAB的度数为 .
14.定义一种新运算:对于任意的非零实数a,b,a b=.若(x﹣1) (x+1)=,则x的值为 .
15.如图,二次函数y=ax2+bx+c(a≠0)图象经过点A(﹣1,﹣2),对称轴为直线x=1,则9a+3b+c的值是 .
16.如图,将矩形OABC的顶点O与原点重合,边AO、CO分别与x、y轴重合.将矩形沿DE折叠,使得点O落在边AB上的点F处,反比例函数上恰好经过E、F两点,若B点的坐标为(2,1),则k的值为 .
三.解答题(共8小题,满分80分)
17.(8分)(1)计算:(2x+1)(2x﹣1)﹣(2x﹣3)2.
(2)解不等式组:.
18.(8分)如图,在6×6的网格中,△ABC的顶点在格点上,仅用无刻度的直尺按要求在网格中作图.
(1)在图1中画出线段AD,点D在BC上,使得S△ACD:S△ABD=1:2;
(2)在图2中画出△ABC的重心E.
19.(8分)观察两个连续偶数的平方差:
②42﹣22=12;②62﹣42=20,③82﹣62=28,……
(1)写出第n个等式,并进行证明;
(2)问172是否可以写成两个连续偶数的平方差?如果能,请写出这两个偶数;如果不能,请说明理由.
20.(8分)新能源车是当下热点,某品牌新能源汽车去年8~12月五个月的销售总量为106万台,图1表示该品牌新能源汽车8~12月各月的销量,图2表示该品牌新能源汽车8~12月各月和上个月的环比增长率,请解答下列问题:
(1)请你根据信息将统计图1补充完整;
(2)增长率最大的是哪个月,增长了多少万台;
(3)小明观察图2后认为,从十月份开始该品牌新能源汽车的销量逐渐降低.他的说法正确吗?请说明理由.
21.(10分)我市的花果山景区大圣湖畔屹立着一座古塔——阿育王塔,是苏北地区现存最高和最古老的宝塔.小明与小亮要测量阿育王塔的高度,如图所示,小明在点A处测得阿育王塔最高点C的仰角∠CAE=45°,再沿正对阿育王塔方向前进至B处测得最高点C的仰角∠CBE=53°,AB=10m;小亮在点G处竖立标杆FG,小亮的所在位置点D、标杆顶F、最高点C在一条直线上,FG=1.5m,GD=2m.
(1)求阿育王塔的高度CE;
(2)求小亮与阿育王塔之间的距离ED.
(注:结果精确到0.01m,参考数据:sin53°≈0.799,cos53°≈0.602,tan53°≈1.327)
22.(12分)乌馒头是江北慈城地方特色点心,用麦粉发酵,再掺以白糖黄糖,蒸制而成.因其用黄糖,颜色暗黄,所以称之谓“乌馒头”.某商店销售乌馒头,通过分析销售情况发现,乌馒头的日销售量y(盒)是销售单价x(元/盒)的一次函数,销售单价、日销售量的部分对应值如下表,已知销售单价不低于成本价且不高于20元,每天销售乌馒头的固定损耗为20元,且销售单价为18元/盒时,日销售纯利润为1180元.
销售单价x(元/盒) 15 13
日销售量y(盒) 500 700
(1)求乌馒头的日销售量y(盒)与销售单价x(元/盒)的函数表达式;
(2)“端午乌馒重阳粽”是慈城的习俗.端午节期间,商店决定采用降价促销的方式回馈顾客.在顾客获得最大实惠的前提下,当乌馒头每盒降价多少元时,商店日销售纯利润为1480元?
(3)当销售单价定为多少时,日销售纯利润最大,并求此日销售最大纯利润.
23.(12分)【基础巩固】
(1)如图1,在△ABC中,D为BC上一点,连结AD,E为AD上一点,连结CE,若∠BAD=∠ACE,CD=CE,求证:△ABD∽△CAE.
【尝试应用】
(2)如图2,在平行四边形ABCD中,对角线AC、BD交于点O,E为OC上一点,连结BE,∠CBE=∠DCO,BE=DO,若BD=12,OE=5,求AC的长.
【拓展提升】
(3)如图3,在菱形ABCD中,对角线AC、BD交于点O,E为BC中点,F为DC上一点,连结OE、AF,∠AEO=∠CAF,若,AC=6,求菱形ABCD的边长.
24.(14分)如图1,AC,BD是⊙O的两条弦,且BD⊥AC于点E.
(1)若AE=BE,求证:DE=CE.
(2)如图2,连结AB,BC,CD,若CA=CD,
①判断∠ACB与∠ACD具有怎样的数量关系,并说明理由.
②在BD上存在点F,满足BF=2AB,M是的中点,连结MF.若,MF=2,求⊙O的半径.
浙江省宁波市2023年中考数学押题密卷
试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.﹣2023的倒数为( )
A.﹣2023 B. C. D.2023
【分析】乘积是1的两数互为倒数,由此即可得到答案.
【解答】解:﹣2023的倒数为﹣.
故选:C.
2.下列计算正确的是( )
A.a3+a3=2a6 B.a3×a3=a6 C.a6÷a3=a2 D.(3a)3=9a3
【分析】利用合并同类项的法则,同底数幂的除法的法则,同底数幂的乘法的法则,积的乘方的法则对各项进行运算即可.
【解答】解:A、a3+a3=2a3,故A不符合题意;
B、a3×a3=a6,故B符合题意;
C、a6÷a3=a3,故C不符合题意;
D、(3a)3=27a3,故D不符合题意;
故选:B.
3.我国研究人员利用中国天眼对致密星系群“斯蒂芬五重星系”及周围天区的氢原子气体进行成像观测,发现了1个尺度大约为200万光年的巨大原子气体系统,尺度比银河系大20倍.长度单位光年是指光在真空中传播一年所经过的距离,大约为9460700000000千米,将数9460700000000用科学记数法表示为( )
A.9.4607×1011 B.9.4607×1012
C.94607×108 D.0.94607×1013
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:9460700000000=9.4607×1012.
故选:B.
4.如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
【分析】根据主视图是从物体的正面看得到的视图解答即可.
【解答】解:从正面看,共有两列,从左到右小正方形的个数分别为3、1.
故选:A.
5.某学习小组9名学生参加“生活中的数学知识竞赛”,他们的得分情况如表:
人数(人) 1 3 4 1
分数(分) 80 85 90 95
那么这9名学生所得分数的众数和中位数分别是( )
A.90,90 B.90,85 C.90,87.5 D.85,85
【分析】众数是一组数据中出现次数最多的数据;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;可得答案.
【解答】解:在这一组数据中90是出现次数最多的,故众数是90;
排序后处于中间位置的那个数是90,那么由中位数的定义可知,这组数据的中位数是90.
故选:A.
6.有5张卡片,正面分别写着“冰墩墩”、“雪容融”、“琮琮”、“莲莲”、“辰辰”,其余都相同,正面朝下放置.小军从中任取一张恰为杭州亚运会吉祥物的概率为( )
(注:“冰墩墩”是北京冬奥会的吉祥物,“雪容融”为北京冬残奥会吉祥物,“琮琮”、“莲莲”、“辰辰”都是杭州亚运会的吉祥物)
A. B. C. D.
【分析】直接根据概率公式求解.
【解答】解:∵5张卡片上有3张为杭州亚运会吉祥物,
∴小军从中任取一张恰为杭州亚运会吉祥物的概率为.
故选:C.
7.如图,在△ABC中,AB=AC,∠A=36°.以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于点N.接着分别以点M,N为圆心,大于长为半径作圆弧,两弧交于点H.作射线BH,交AC于点D.再以点D为圆心,DC长为半径作圆弧,交BC于点E,连结DE.则下列说法错误的是( )
A.AD=BD B.∠BDC=∠BCD C. D.△BED∽△BDA
【分析】由作图得BD平分∠ABC,DE=DC,由AB=AC,∠A=36°,得∠ABC=∠ACB=72°,则∠ABD=∠CBD=36°=∠A,所以AD=BD,可判断A正确;因为∠BDC=∠ABD+∠A=72°,∠BCD=72°,所以∠BDC=∠BCD,可判断B正确;因为∠DEC=∠DCE=72°,所以∠EDB=∠DEC﹣∠CBD=36°,则∠EDB=∠CBD,所以BE=DE=DC,由∠DBE=∠ABD=36°,∠EDB=∠A=36°,得△BED∽△BDA,可判断D正确;由=,得=,则AD2=DC AC,可证明AD=BE≠BE,可判断C错误,于是得到问题的答案.
【解答】解:由作图得BD平分∠ABC,DE=DC,
∵AB=AC,∠A=36°,
∴∠ABC=∠ACB==72°,
∴∠ABD=∠CBD=∠ABC=×72°=36°,
∴∠ABD=∠A,
∴AD=BD,
故A正确;
∵∠BDC=∠ABD+∠A=36°+36°=72°,∠BCD=72°,
∴∠BDC=∠BCD,
故B正确;
∵DE=DC,
∴∠DEC=∠DCE=72°,
∴∠EDB=∠DEC﹣∠CBD=72°﹣36°=36°,
∴∠EDB=∠CBD,
∴BE=DE=DC,
∵∠DBE=∠ABD=36°,∠EDB=∠A=36°,
∴△BED∽△BDA,
故D正确;
∴=,
∴=,
∴AD2=DC AC,
设AD=x,BE=DC=m,则AC=x+m,
∴x2=m(x+m),
解关于x的方程得x1=m,x2=m(不符合题意,舍去),
∴AD=BE≠BE,
故C错误,
故选:C.
8.我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:现在有数人一起去买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问共有多少人,物品的价格是多少钱?若设人数共有x人,物品的价格为y钱,可列方程组为( )
A. B.
C. D.
【分析】根据题意可以找出题目中的等量关系,列出相应的方程组,从而可以解答本题.
【解答】解:由题意可得,.
故选:D.
9.如图,已知圆锥侧面展开图的扇形面积为65πcm2,扇形的弧长为10πcm,则圆锥的高是( )
A.5cm B.10cm C.12cm D.13cm
【分析】圆锥的侧面积=×弧长×母线长,把相应数值代入即可求解可得圆锥的母线长,然后可以利用勾股定理求得圆锥的高.
【解答】解:设母线长为R,由题意得:65π=×10π×R,解得R=13cm.
设圆锥的底面半径为r,则10π=2πr,
解得:r=5,
故圆锥的高为:=12
故选:C.
10.如图,一次函数y1=kx+b(k≠0)与反比例函数的图象相交于A(1,2),B(﹣2,a)两点,则不等式kx+b﹣<0的解是( )
A.x<﹣2 B.x<﹣2或0<x<1
C.﹣2<x<0或x>1 D.x<1
【分析】一次函数y1=kx+b落在与反比例函数的图象下方的部分对应的自变量的取值范围即为所求.
【解答】解:∵一次函数y1=kx+b(k≠0)与反比例函数的图象相交于A(1,2),B(﹣2,a)两点,
∴不等式kx+b﹣<0的解集是x<﹣2或0<x<1.
故选:B.
二.填空题(共6小题,满分30分,每小题5分)
11.= 2 .
【分析】利用算术平方根定义计算即可求出值.
【解答】解:∵22=4,
∴4的算术平方根是2,即=2.
故答案为:2.
12.分解因式:x2﹣4= (x+2)(x﹣2) .
【分析】直接利用平方差公式进行因式分解即可.
【解答】解:x2﹣4=(x+2)(x﹣2).
故答案为:(x+2)(x﹣2).
13.如图,以AB为直径的⊙O与BC相切于点B,交AC于点D.若∠CBD=30°,则∠CAB的度数为 30° .
【分析】利用圆的切线的性质定理∠CBD+∠ABD=90°,利用圆周角定理得到∠CAB+∠ABD=90°,利用同角的余角相等即可得出结论.
【解答】解:∵以AB为直径的⊙O与BC相切于点B,
∴AB⊥BC,
∴∠ABC=90°,
∴∠CBD+∠ABD=90°.
∵AB为直径,
∴∠ADB=90°,
∴∠CAB+∠ABD=90°,
∴∠CAB=∠CBD=30°.
故答案为:30°.
14.定义一种新运算:对于任意的非零实数a,b,a b=.若(x﹣1) (x+1)=,则x的值为 x=2 .
【分析】根据题干的新定义,得到.再解这分式方程,进而求得x.
【解答】解:由题意得,.
去分母,得x+1+x﹣1=3x﹣2.
移项,得x+x﹣3x=﹣2+1﹣1.
合并同类项,得﹣x=﹣2.
x的系数化为1,得x=2.
检验:当x=2,(x+1)(x﹣1)≠0.
∴该分式方程的解为x=2.
故答案为:x=2.
15.如图,二次函数y=ax2+bx+c(a≠0)图象经过点A(﹣1,﹣2),对称轴为直线x=1,则9a+3b+c的值是 ﹣2 .
【分析】根据抛物线的轴对称性质得到:当x=3与当x=﹣1时,所对应的y值相等,据此解答.
【解答】解:∵二次函数y=ax2+bx+c(a≠0)图象经过点A(﹣1,﹣2),对称轴为直线x=1,
∴点A(﹣1,﹣2)关于直线x=1对称的点的坐标为(3,﹣2).
∴当x=3时,y=﹣2,
即9a+3b+c=﹣2.
故答案为:﹣2.
16.如图,将矩形OABC的顶点O与原点重合,边AO、CO分别与x、y轴重合.将矩形沿DE折叠,使得点O落在边AB上的点F处,反比例函数上恰好经过E、F两点,若B点的坐标为(2,1),则k的值为 10﹣2 .
【分析】连结OF,过E作EH⊥OA于H,由B点坐标为(2,1),即可得出E点的坐标为(k,1),F点的坐标为,证得△EHD∽△OAF,得到,求得,进而求得,,由折叠可得,利用勾股定理得到关于k的方程,解方程即可求得k的值.
【解答】解:连结OF,过E作EH⊥OA于H.
∵B点坐标为(2,1),
∴E点的纵坐标为1,F点的横坐标为2,
∵反比例函数上恰好经过E、F两点,
∴E点的坐标为(k,1),F点的坐标为,
∵∠EDH+∠AOF=∠EDH+∠HED=90°,
∴∠AOF=∠HED,
又∠EHD=∠OAF=90°,
∴△EHD∽△OAF,
∴,即,
∴,
∴,,
由折叠可得,
在Rt△DAF中,由勾股定理可得,
解得,(舍).
∴k的值为10﹣2.
故答案为:10﹣2.
三.解答题(共8小题,满分80分)
17.(8分)(1)计算:(2x+1)(2x﹣1)﹣(2x﹣3)2.
(2)解不等式组:.
【分析】(1)先用平方差公式、完全平方公式,再合并同类项;
(2)先解不等式组中的各不等式,再确定不等式组的解集.
【解答】解:(1)原式=4x2﹣1﹣(4x2﹣12x+9)
=4x2﹣1﹣4x2+12x﹣9
=12x﹣10;
(2),
解①得x>﹣2,
解②得x≤2.
∴不等式组的解集为﹣2<x≤2.
18.(8分)如图,在6×6的网格中,△ABC的顶点在格点上,仅用无刻度的直尺按要求在网格中作图.
(1)在图1中画出线段AD,点D在BC上,使得S△ACD:S△ABD=1:2;
(2)在图2中画出△ABC的重心E.
【分析】(1)取格点P,Q连接PQ交BC于点D,连接AD即可;
(2)作直线BM,CN交于点E,点E即为所求.
【解答】解:(1)如图1中,点D即为所求;
(2)如图2中,点E即为所求.
19.(8分)观察两个连续偶数的平方差:
②42﹣22=12;②62﹣42=20,③82﹣62=28,……
(1)写出第n个等式,并进行证明;
(2)问172是否可以写成两个连续偶数的平方差?如果能,请写出这两个偶数;如果不能,请说明理由.
【分析】(1)根据给定的例子可得第n个等式是:(2n+2)2﹣(2n)2=4(2n+1),根据平方差公式的逆运算证明即可;
(2)当8n+4=172时,解得n=21,即可确定答案.
【解答】解:(1)第n个等式是:(2n+2)2﹣(2n)2=4(2n+1),证明如下:
∵(2n+2)2﹣(2n)2
=(2n+2+2n)(2n+2﹣2n)
=2(4n+2)
=4(2n+1),
∴(2n+2)2﹣(2n)2=4(2n+1).
(2)172可以写成两个连续偶数的平方差,这两个偶数是42和44,理由如下:
当8n+4=172时,解得n=21,
∴2n=2×21=42,2n+2=42+2=44,
∴两个偶数分别为42和44.
20.(8分)新能源车是当下热点,某品牌新能源汽车去年8~12月五个月的销售总量为106万台,图1表示该品牌新能源汽车8~12月各月的销量,图2表示该品牌新能源汽车8~12月各月和上个月的环比增长率,请解答下列问题:
(1)请你根据信息将统计图1补充完整;
(2)增长率最大的是哪个月,增长了多少万台;
(3)小明观察图2后认为,从十月份开始该品牌新能源汽车的销量逐渐降低.他的说法正确吗?请说明理由.
【分析】(1)用销售总量减去其他四个月的销售量可得9月份的销售量,进而补全条形统计图;
(2)结合统计图数据列式计算即可;
(3)根据增长率的定义解答即可.
【解答】解:(1)由题意可知,9月份销量为106﹣(17.5+22+23+23.5)=20(万台).
所补作图形如图所示:
(2)由题意可知,9月增长率最高为14.3%,增长了20﹣17.5=2.5(万台);
(3)小明的说法是错误的,理由如下:
因为10~12月份只是增长率降低,但是增长率仍为正,说明销量仍在增加(答案不唯一).
21.(10分)我市的花果山景区大圣湖畔屹立着一座古塔——阿育王塔,是苏北地区现存最高和最古老的宝塔.小明与小亮要测量阿育王塔的高度,如图所示,小明在点A处测得阿育王塔最高点C的仰角∠CAE=45°,再沿正对阿育王塔方向前进至B处测得最高点C的仰角∠CBE=53°,AB=10m;小亮在点G处竖立标杆FG,小亮的所在位置点D、标杆顶F、最高点C在一条直线上,FG=1.5m,GD=2m.
(1)求阿育王塔的高度CE;
(2)求小亮与阿育王塔之间的距离ED.
(注:结果精确到0.01m,参考数据:sin53°≈0.799,cos53°≈0.602,tan53°≈1.327)
【分析】(1)由∠CAE=45°,AB=10m,可得BE=AE﹣10=CE﹣10,在Rt△CEB中,可得tan∠CBE=tan53°==,即可解得阿育王塔的高度CE约为40.58m;
(2)由△FGD∽△CED,可得=,可解得小亮与阿育王塔之间的距离ED是54.11m.
【解答】解:(1)在Rt△CAE中,
∵∠CAE=45°,
∴CE=AE,
∵AB=10m,
∴BE=AE﹣10=CE﹣10,
在Rt△CEB中,
tan∠CBE=tan53°==,
∴1.327≈,
解得CE≈40.58(m);
答:阿育王塔的高度CE约为40.58m;
(2)由题意知:∠CED=90°=∠FGD,∠FDG=∠CDE,
∴△FGD∽△CED,
∴=,即=,
解得ED≈54.11(m),
答:小亮与阿育王塔之间的距离ED约是54.11m.
22.(12分)乌馒头是江北慈城地方特色点心,用麦粉发酵,再掺以白糖黄糖,蒸制而成.因其用黄糖,颜色暗黄,所以称之谓“乌馒头”.某商店销售乌馒头,通过分析销售情况发现,乌馒头的日销售量y(盒)是销售单价x(元/盒)的一次函数,销售单价、日销售量的部分对应值如下表,已知销售单价不低于成本价且不高于20元,每天销售乌馒头的固定损耗为20元,且销售单价为18元/盒时,日销售纯利润为1180元.
销售单价x(元/盒) 15 13
日销售量y(盒) 500 700
(1)求乌馒头的日销售量y(盒)与销售单价x(元/盒)的函数表达式;
(2)“端午乌馒重阳粽”是慈城的习俗.端午节期间,商店决定采用降价促销的方式回馈顾客.在顾客获得最大实惠的前提下,当乌馒头每盒降价多少元时,商店日销售纯利润为1480元?
(3)当销售单价定为多少时,日销售纯利润最大,并求此日销售最大纯利润.
【分析】(1)设y=kx+b,根据表格即可求解;
(2)根据:销售量×单件利润﹣损耗费用=销售总利润,列出方程即可求解;
(3)设日销售纯利润为w元,根据:销售量×单件利润﹣损耗费用=销售总利润,列出函数关系式,并在12≤x≤20求最值即可.
【解答】解:(1)设y=kx+b,由题意得
,
解得,
∴y=﹣100x+2000.
(2)当x=18时,y=200,
即销售200盒的纯利润为1180元,
∴成本价为:18﹣(1180+20)÷200=12(元),
(﹣100x+2000)(x﹣12)=1480+20,
解得:x1=17(舍),x2=15,
18﹣15=3(元).
答:当乌馒头每盒降价3元时,商店每天获利为1480元.
(3)设日销售纯利润为w元,由题意得
w=(﹣100x+2000)(x﹣12)﹣20
=﹣100x2+3200x﹣24020
=﹣100(x﹣16)2+1580,
∵﹣100<0,12≤x≤20,
∴当x=16时,w有最大值1580元,
答:当销售单价定为16元/盒时,日销售纯利润最大,最大纯利润为1580元.
23.(12分)【基础巩固】
(1)如图1,在△ABC中,D为BC上一点,连结AD,E为AD上一点,连结CE,若∠BAD=∠ACE,CD=CE,求证:△ABD∽△CAE.
【尝试应用】
(2)如图2,在平行四边形ABCD中,对角线AC、BD交于点O,E为OC上一点,连结BE,∠CBE=∠DCO,BE=DO,若BD=12,OE=5,求AC的长.
【拓展提升】
(3)如图3,在菱形ABCD中,对角线AC、BD交于点O,E为BC中点,F为DC上一点,连结OE、AF,∠AEO=∠CAF,若,AC=6,求菱形ABCD的边长.
【分析】(1)可证得∠CDE=∠CED,从而∠ADB=∠CEA,进一步得出结论;
(2)可证得∠BEO=∠BOE,从而得出∠BEC=∠COD,进而得出△BEC∽△COD,从而,设OC=x,则CE=OC﹣OE=x﹣5,从而得出,从而求得x的值,进一步得出结果;
(3)延长AG,BC,交于点G,可得出△CGF∽△DAF,从而,进而表示出CG,可证得△AOE∽△GCA,从而,进而求得t的值,进一步得出结果.
【解答】(1)证明:∵CD=CE,
∴∠CDE=∠CED,
∴180°﹣∠CDE=180°﹣∠CED,
∴∠ADB=∠CEA,
∵∠BAD=∠ACE,
∴△ABD∽△CAE.
(2)解:∵四边形ABCD是平行四边形,
∴,
∴BE=DO=BO=6.
∴∠BEO=∠BOE,
∴180°﹣∠BEO=180°﹣∠BOE,
∴∠BEC=∠COD.
∵∠CBE=∠DCO,
∴△BEC∽△COD,
∴,
设OC=x,则CE=OC﹣OE=x﹣5,
∴,
∴x1=9,x2=﹣4(舍去),
∴OC=9,
∴AC=2OC=18;
(3)解:如图,
延长AG,BC,交于点G.
∵,
∴设DF=5t,FC=3t,则CD=8t,
∵四边形ABCD是菱形,
∴AB=AD=BC=CD=8t,AD∥BC,,AC⊥BD,
∴△CGF∽△DAF,
∴,
即,
∴.
在Rt△BOC中,
∵E为BC的中点,
∴OE=CE=BC=4t.
∴∠COE=∠ACE,
∴∠AOE=∠ACG,
∵∠AEO=∠CAF,
∴△AOE∽△GCA,
∴,
即,
∴t1=,t2=﹣(舍去),
∴,
即菱形ABCD的边长为.
24.(14分)如图1,AC,BD是⊙O的两条弦,且BD⊥AC于点E.
(1)若AE=BE,求证:DE=CE.
(2)如图2,连结AB,BC,CD,若CA=CD,
①判断∠ACB与∠ACD具有怎样的数量关系,并说明理由.
②在BD上存在点F,满足BF=2AB,M是的中点,连结MF.若,MF=2,求⊙O的半径.
【分析】(1)连接AD,BC.证明△ADE∽△BCE,由相似三角形的性质得出,进一步得出结论;
(2)①作OF⊥AC于F,作OG⊥CD于G,可推出OC平分∠ACD,可推出∠A+∠ACH=90°,∠A+∠ADE=90°,进而∠ADE=∠ACH,进一步得出结果;
②连接CM,交BD于H,连接AM,作AG∥MF,交BD于G,可推出△CEH∽△CAM,四边形AGFM是平行四边形,从而,AG=MF=2,FG=AM=2,进而得出FG的长,可推出EH=EB,设BE=x,则EG=﹣x,由AE2=AG2﹣EG2=AB2﹣BE2,列出22﹣(2﹣x)2=(2)2﹣x2,从而求得x的值,则求出BE及AE的长,由比例线段可求出CE,进一步得出结果.
【解答】(1)证明:如图1,
连接AD,BC,
∵,,
∴∠D=∠C,∠A=∠B,
∴△ADE∽△BCE,
∴,
∵AE=BE,
∴DE=CE;
(2)解:①如图2,
∠ACB=∠ACD,理由如下:
作OF⊥AC于F,作OG⊥CD于G,
CF=AC,CG=CD,
∵AC=CD,
∴CF=CG,
∴∠COF=∠COG,
∴∠ACO=∠DCO,
∴CH⊥AD,
∴∠AHC=90°,
∴∠A+∠ACH=90°,
∵BD⊥AC,
∴∠AED=90°,
∴∠A+∠ADE=90°,
∴∠ADE=∠ACH,
∵∠ACB=∠ADE,
∴∠ACB=∠ACH=∠ACD;
②如图3,
连接CM,交BD于H,连接AM,作AG∥MF,交BD于G,
∴∠MAC=90°,
∵BD⊥AC,
∴∠DEC=90°,
∴∠DEC=∠MAC,
∴AM∥BD,
∴△CEH∽△CAM,四边形AGFM是平行四边形,
∴,AG=MF=2,FG=AM,
由①得,
∠ACB=∠ACM,
∴=,
∴AM=AB=2,
∴FG=2,
∴BG=BF﹣FG=2,
∵∠CEB=∠CEH=90°,
∴∠CHE=∠CBE,
∴CH=CB,
∴EH=EB,
设BE=x,则EG=2﹣x,
由AE2=AG2﹣EG2=AB2﹣BE2,
∴22﹣(2﹣x)2=(2)2﹣x2,
∴x=,
∴EH=BE=,
∴AE=(2)2﹣()2,
∴AE=,
∴,
∴CE=,
∴AC=CE+AE=2,
∴CM===8,
∴圆的半径为4.
同课章节目录
