1.1.1 第2课时 共线向量与共面向量 课件(共32张PPT)
文档属性
| 名称 | 1.1.1 第2课时 共线向量与共面向量 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-09 16:19:39 | ||
图片预览











文档简介
(共32张PPT)
第2课时 共线向量与共面向量
第一章 1.1.1 空间向量及其线性运算
学习目标
1.理解向量共线、向量共面的定义.
2.掌握向量共线的充要条件和向量共面的充要条件,会证明空间三点共线、四点共面.
导语
我们知道向量是有大小、有方向的量,它可以平行移动,平面内两个向量若方向相同或相反,就说它们是共线的,那么在空间内向量共线又是怎么回事呢?今天我们就来探究一下.
一、空间向量共线的充要条件
二、空间向量共面的充要条件
随堂演练
课时对点练
内容索引
空间向量共线的充要条件
一
问题1 平面向量共线的充要条件是什么?它适用于空间向量吗?
提示 对任意两个平面向量a,b(b≠0),a∥b的充要条件是存在实数λ,使a=λb,由于空间向量共线的定义与平面向量相同,因此也适用于空间向量.
知识梳理
1.对任意两个空间向量a,b(b≠0),a∥b的充要条件是存在实数λ,使______.
2.如图,O是直线l上一点,在直线l上取非零向量a,则对于直线l上任意一点P,由数乘向量的定义及向量共线的充要条件可知,存在实数λ,使得 =λa,把与向量a平行的非零向量称为直线l的 ,直线l上任意一点都可以由直线l上的一点和它的方向向量表示.
方向向量
a=λb
(1)直线可以由其上一点和它的方向向量确定.
(2)向量a,b共线时,表示向量a,b的两条有向线段不一定在同一条直线上.
注意点:
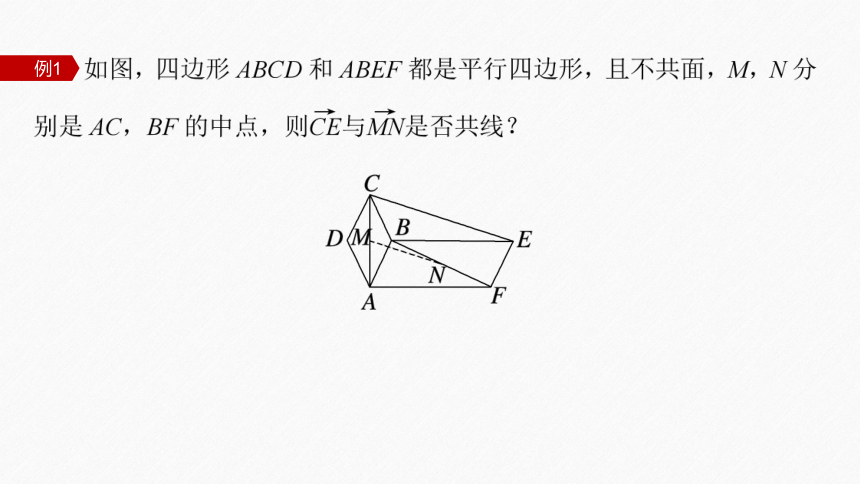
例1
方法一 ∵M,N分别是AC,BF的中点,且四边形ABCD和ABEF都是平行四边形,
方法二 ∵M,N分别是AC,BF的中点,且四边形ABCD和ABEF都是平行四边形,
向量共线的判定及应用
(1)判断或证明两向量a,b(b≠0)共线,就是寻找实数λ,使a=λb成立,为此常结合题目图形,运用空间向量的线性运算法则将目标向量化简或用同一组向量表达.
(2)判断或证明空间中的三点(如P,A,B)共线的方法:是否存在实数λ,使
反思感悟
跟踪训练1
1
所以m+n=1.
∵E,H分别是AB,AD的中点,
又F不在直线EH上,
∴四边形EFGH是梯形.
空间向量共面的充要条件
二
问题2 空间任意两个向量是共面向量,则空间任意三个向量是否共面?
提示 不一定,如图所示,空间中的三个向量不共面.
问题3 对两个不共线的空间向量a,b,如果p=xa+yb,那么向量p与向量a,b有什么位置关系?反过来,向量p与向量a,b有什么位置关系时,p=xa+yb?
提示 向量p与不共线向量a,b共面的充要条件是存在唯一的有序实数对(x,y),使p=xa+yb.
知识梳理
1.向量与平面平行:如果表示向量a的有向线段 所在的直线OA______
______或 ,那么称向量a平行于平面α.
2.共面向量
平行于
在平面α内
平面α
定义 平行于同一个 的向量
三个向量共面的充要条件 向量p与不共线向量a,b共面的充要条件是存在 的有序实数对(x,y)使__________
唯一
平面
p=xa+yb
提示 x+y+z=1.
证明如下:(1)充分性
∴点P与A,B,C共面.
(2)必要性
∵点P在平面ABC内,不共线的三点A,B,C,
又∵点O在平面ABC外,
∴x=1-m-n,y=m,z=n,
∴x+y+z=1.
例2
√
√
由共面的充要条件知P,A,B,C四点共面,故C选项正确;
(2)(链接教材P5例1)如图所示,在长方体ABCD-A1B1C1D1中,M为DD1的中点,N∈AC,且AN∶NC=2,求证:A1,B,N,M四点共面.
又∵三向量有相同的起点A1,
∴A1,B,N,M四点共面.
向量共面的判定及应用
(1)证明三个向量共面(或四点共面)时,可以通过以下几个条件进行证明.
反思感悟
反思感悟
已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,求证:
E,F,G,H四点共面.
跟踪训练2
如图,连接EG,BG.
课堂
小结
1.知识清单:
(1)空间向量共线的充要条件,直线的方向向量.
(2)空间向量共面的充要条件.
(3)三点共线、四点共面的证明方法.
2.方法归纳 :转化化归、类比.
3.常见误区:混淆向量共线与线段共线、点共线.
第2课时 共线向量与共面向量
第一章 1.1.1 空间向量及其线性运算
学习目标
1.理解向量共线、向量共面的定义.
2.掌握向量共线的充要条件和向量共面的充要条件,会证明空间三点共线、四点共面.
导语
我们知道向量是有大小、有方向的量,它可以平行移动,平面内两个向量若方向相同或相反,就说它们是共线的,那么在空间内向量共线又是怎么回事呢?今天我们就来探究一下.
一、空间向量共线的充要条件
二、空间向量共面的充要条件
随堂演练
课时对点练
内容索引
空间向量共线的充要条件
一
问题1 平面向量共线的充要条件是什么?它适用于空间向量吗?
提示 对任意两个平面向量a,b(b≠0),a∥b的充要条件是存在实数λ,使a=λb,由于空间向量共线的定义与平面向量相同,因此也适用于空间向量.
知识梳理
1.对任意两个空间向量a,b(b≠0),a∥b的充要条件是存在实数λ,使______.
2.如图,O是直线l上一点,在直线l上取非零向量a,则对于直线l上任意一点P,由数乘向量的定义及向量共线的充要条件可知,存在实数λ,使得 =λa,把与向量a平行的非零向量称为直线l的 ,直线l上任意一点都可以由直线l上的一点和它的方向向量表示.
方向向量
a=λb
(1)直线可以由其上一点和它的方向向量确定.
(2)向量a,b共线时,表示向量a,b的两条有向线段不一定在同一条直线上.
注意点:
例1
方法一 ∵M,N分别是AC,BF的中点,且四边形ABCD和ABEF都是平行四边形,
方法二 ∵M,N分别是AC,BF的中点,且四边形ABCD和ABEF都是平行四边形,
向量共线的判定及应用
(1)判断或证明两向量a,b(b≠0)共线,就是寻找实数λ,使a=λb成立,为此常结合题目图形,运用空间向量的线性运算法则将目标向量化简或用同一组向量表达.
(2)判断或证明空间中的三点(如P,A,B)共线的方法:是否存在实数λ,使
反思感悟
跟踪训练1
1
所以m+n=1.
∵E,H分别是AB,AD的中点,
又F不在直线EH上,
∴四边形EFGH是梯形.
空间向量共面的充要条件
二
问题2 空间任意两个向量是共面向量,则空间任意三个向量是否共面?
提示 不一定,如图所示,空间中的三个向量不共面.
问题3 对两个不共线的空间向量a,b,如果p=xa+yb,那么向量p与向量a,b有什么位置关系?反过来,向量p与向量a,b有什么位置关系时,p=xa+yb?
提示 向量p与不共线向量a,b共面的充要条件是存在唯一的有序实数对(x,y),使p=xa+yb.
知识梳理
1.向量与平面平行:如果表示向量a的有向线段 所在的直线OA______
______或 ,那么称向量a平行于平面α.
2.共面向量
平行于
在平面α内
平面α
定义 平行于同一个 的向量
三个向量共面的充要条件 向量p与不共线向量a,b共面的充要条件是存在 的有序实数对(x,y)使__________
唯一
平面
p=xa+yb
提示 x+y+z=1.
证明如下:(1)充分性
∴点P与A,B,C共面.
(2)必要性
∵点P在平面ABC内,不共线的三点A,B,C,
又∵点O在平面ABC外,
∴x=1-m-n,y=m,z=n,
∴x+y+z=1.
例2
√
√
由共面的充要条件知P,A,B,C四点共面,故C选项正确;
(2)(链接教材P5例1)如图所示,在长方体ABCD-A1B1C1D1中,M为DD1的中点,N∈AC,且AN∶NC=2,求证:A1,B,N,M四点共面.
又∵三向量有相同的起点A1,
∴A1,B,N,M四点共面.
向量共面的判定及应用
(1)证明三个向量共面(或四点共面)时,可以通过以下几个条件进行证明.
反思感悟
反思感悟
已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,求证:
E,F,G,H四点共面.
跟踪训练2
如图,连接EG,BG.
课堂
小结
1.知识清单:
(1)空间向量共线的充要条件,直线的方向向量.
(2)空间向量共面的充要条件.
(3)三点共线、四点共面的证明方法.
2.方法归纳 :转化化归、类比.
3.常见误区:混淆向量共线与线段共线、点共线.
