沪科版2022-2023学年度下学期七年级期末练习数学试2(含解析)
文档属性
| 名称 | 沪科版2022-2023学年度下学期七年级期末练习数学试2(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-09 21:42:31 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
沪科版2022-2023学年度下学期七年级期末练习数学试2
姓名:__________班级:__________考号:__________总分__________
一、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.下列式子正确的是( )
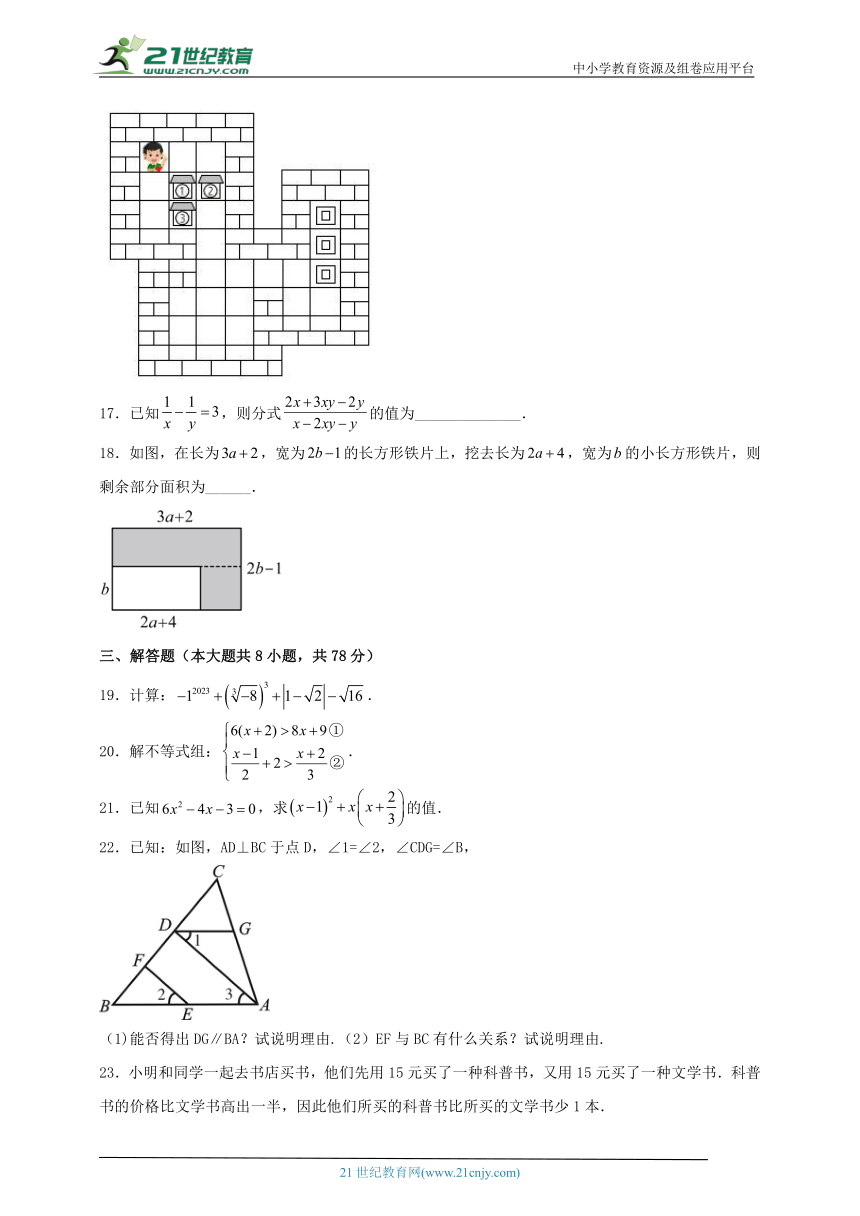
A. B. C. D.
2.下列四个实数中,最大的数是( )
A. B. C. D.
3.下列各式计算正确的是( )
A. B. C. D.
4.如图,直线,,则的度数是( )
A. B. C. D.
5.口味虾、臭豆腐、嗦螺和糖油粑粑是是长沙著名的小吃,某兴趣小组在班级发动了一项“舌尖上的长沙-我最喜欢的长沙小吃”调查活动,发现结果满足以下三个条件:
(1)喜欢嗦螺的人数少于喜欢口味虾的人数;
(2)喜欢嗦螺的人数多于喜欢臭豆腐的人数;
(3)喜欢臭豆腐的人数的3倍多于喜欢口味虾的人数.
若喜欢臭豆腐的人数为6,则喜欢嗦螺的人数的最大值为( )
A.16 B.6 C.17 D.7
6.用如图所示的正方形和长方形卡片若干张,拼成一个长为,宽为的长方形,需要类卡片( )张.
A.3 B.4 C.5 D.6
7.下列分式方程有解的是( )
A. B.
C. D.
8.如图:能判断的条件是( )
A. B. C. D.
9.若:,,,则:代数式的值等于( )
A. B. C. D.
10.多项式的公因式是( )
A. B. C. D.
11.下列判断正确的是( )
A.若x为有理数,则 B.若x为有理数,则
C.若,则 D.若,则
12.如果不等式的正整数解是1,2,3,那么的取值范围是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分)
13.若,,则___________________.
14.不等式组的解集为_____.
15.用“”定义一种新运算:对于任意有理数和,规定,若,则的值为___________.
16.庆庆是一位特别喜欢学习数学的小朋友,周末这天他做完作业,在手机上找了一款数学相关的益智类游戏《推箱子》,要求将图中编号为①②③的三个箱子分别推进图中“回”字的位置.如果庆庆要想一次性通关,且尽可能让自己步数少,应该先推( )号箱子,再推( )号箱子,最后推( )号箱子.
17.已知,则分式的值为______________.
18.如图,在长为,宽为的长方形铁片上,挖去长为,宽为的小长方形铁片,则剩余部分面积为______.
三、解答题(本大题共8小题,共78分)
19.计算:.
20.解不等式组:.
21.已知,求的值.
22.已知:如图,AD⊥BC于点D,∠1=∠2,∠CDG=∠B,
(1)能否得出DG∥BA?试说明理由.(2)EF与BC有什么关系?试说明理由.
23.小明和同学一起去书店买书,他们先用15元买了一种科普书,又用15元买了一种文学书.科普书的价格比文学书高出一半,因此他们所买的科普书比所买的文学书少1本.
(1)这种科普书和这种文学书的价格各是多少?
(2)若准备用60元购买科普书和文学书两种书共10本,则至少要购买文学书多少本?
24.某商店从批发商处购进甲、乙两种产品,购进5件甲产品和8件乙产品需要成本170元,购进2件甲产品和4件乙产品需要成本80元.销售时,每件甲产品售价为20元,每件乙产品售价为35元.
(1)求每件甲产品和每件乙产品的成本价;
(2)若商店从批发商处购进甲、乙两种产品共100件,购进时总成本不超过1300元,且全部销售完以后利润不低于1580元,请问有几种购进方案?
25.由完全平方差公式可知,,而,所以,对所有的实数都有:,且只有当时,才有等号成立:.
应用上面的结论解答下列问题:
(1)计算 ,由此可知 (填不等号);
(2)已知为不相等的两正数,试比较:与的大小;
(3)试求分式的最大值.
26.如图1,已知两条直线,被直线所截,分别交于点,点,平分交于点,且.
(1)判断直线与直线是否平行,并说明理由;
(2)如图2,点是射线上一动点(不与点,重合),平分交于点,过点作于点,设,.
①当点在点的右侧时,若,求的度数;
②当点在运动过程中,与之间有怎样的数量关系?请写出你的猜想,并加以证明
参考答案:
1.【分析】分别根据合并同类项法则,幂的乘方运算法则,同底数幂的乘法法则以及完全平方公式逐一判断即可.
解:A、,故本选项符合题意;
B、,故本选项不合题意;
C、与不是同类项,所以不能合并,故本选项不合题意;
D、,故本选项不合题意;
故选:A.
【点评】本题主要考查了同底数幂的乘法,合并同类项,完全平方公式以及幂的乘方,熟记相关公式与运算法则是解答本题的关键.
2.【分析】根据实数的大小比较即可求解.
解: ∵ ,
∴这四个实数中,最大的数是,
故选:C.
【点评】本题考查了实数的大小比较法则,熟练掌握实数的大小比较法则是解题关键.
3.【分析】根据算术平方根,零指数幂,负整数指数幂,合并同类项,化简绝对值,逐项分析判断即可求解.
解:A. ,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项正确,符合题意;
D. ,故该选项不正确,不符合题意;
故选:C.
【点评】本题考查了算术平方根,零指数幂,负整数指数幂,合并同类项,化简绝对值,熟练掌握算术平方根,零指数幂,负整数指数幂,合并同类项,化简绝对值是解题的关键.
4.【分析】根据平行线的性质可得,再根据,即可得到答案.
解:如图所示,
,
,,
,
,
,
故选:A.
【点评】本题主要考查了平行线的性质、互补的定义,熟练掌握两直线平行,同位角相等,是解题的关键.
5.【分析】设喜欢嗦螺的人数是x,喜欢口味虾的人数是y,根据题意列出不等式组即可解答.
设喜欢嗦螺的人数是x,喜欢口味虾的人数是y,
根据喜欢臭豆腐的人数是6人,
结合题意有:,且x和y都是正整数,
解得:,且x和y都是正整数,
即喜欢口味虾的人数最多为17人,则喜欢嗦螺的人数最多为16人,
故选:A.
【点评】本题考查了不等式组的应用,根据题意列出不等式组是解答本题的关键.
6.【分析】根据长方形的面积公式即可得出结果.
解:∵ 长方形长为,宽为
∴长方形的面积:
∴需要B内卡片5张.
故选C.
【点评】本题考查多项式的乘法,灵活运用多项式乘法法则和数形结合思想是解题的关键.
7.【分析】分别解分式方程,即可求解.
解:A.
方程两边同时乘以得,
解得:,
经检验是原方程的增根,则原方程无解;故该选项不正确,不符合题意;
B. ,方程两边同时乘以,得,
∵,
∴原方程无解;故该选项不正确,不符合题意;
C. ,去分母得,不成立,
∴原方程无解;故该选项不正确,不符合题意;
D. ,去分母得,解得:,
经检验,是原方程的解,故该选项正确,符合题意;
故选:D.
【点评】本题考查了解分式方程,熟练掌握解分式方程的步骤是解题的关键.
8.【分析】根据平行线的判定方法对各选项进行判断.
解:A.当时,根据内错角相等,两直线平行,可以判定,故A符合题意;
B.当时,无法判断,故B不符合题意;
C.当时,无法判断,故C不符合题意;
D.当时,无法判断,故D不符合题意.
故答案选:A.
【点评】本题考查了平行线的判定,解题的关键是熟练掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
9.【分析】首先根据题意,联立方程组,得出,用字母表示出、的值,然后把、的值代入代数式,计算即可得出结果.
解:∵,,
∴,
由,可得:,
把代入,可得:,
又∵,
∴
.
故选:D
【点评】本题考查了二元一次方程组的解法、分式的化简求值,解本题的关键在根据已知二元一次方程组进行消元,将分式中的三个未知数化成只含一个未知数的式子表示.
10.【分析】根据多项式的公因式的确定方法,即可求解.
解:多项式的公因式是,
故选C.
【点评】本题考查了公因式的定义.确定多项式中各项的公因式,可概括为三“定”:①定系数,即确定各项系数的最大公约数;②定字母,即确定各项的相同字母因式(或相同多项式因式);③定指数,即各项相同字母因式(或相同多项式因式)的指数的最低次幂.
11.【分析】根据不等式的基本性质判断即可.
解:,,
,
A错误;
,,
,
C错误;
,,
D错误;
∵,
∴,即成立,
∴B选项正确,
故选B.
【点评】本题考查了不等式的基本性质,熟练运用不等式的基本性质是解题关键.
12.【分析】先求出不等式的解集,再根据其正整数解列出不等式,解此不等式即可求解.
解:解不等式得到:,
正整数解为,,,
,
解得.
故选:.
【点评】本题考查了一元一次不等式的整数解,根据的取值范围正确确定的范围是解题的关键.再解不等式时要根据不等式的基本性质.
13.【分析】将变形为即可求解.
解:,
.
故答案为:
【点评】本题考查求一个数的算术平方根,将变形为是解题的关键.
14.【分析】分别解出每个不等式,再根据“同大取大,同小取小,大小小大中间找,大大小小找不到”确定公共解集即可.
解:
解不等式①,得:,
解不等式②,得:,
∴原不等式组的解集为.
故答案为:.
【点评】本题考查解一元一次不等式组.掌握求不等式组解集的口诀“同大取大,同小取小,大小小大中间找,大大小小找不到”是解题关键.
15.【分析】根据题目中的新定义,理解公式并利用公式将已知条件转化为方程,最后得出结论.
解:∵,
∴,
∵,
∴,
∴,
∴经检验:是分式方程的解,
故答案为:.
【点评】本题有理数的混合运算,解分式方程,注意检验,解答本题的关键是根据新运算列出方程.
16.【分析】要一次性通关,先推阻碍其它箱子的箱子,然后推动其它箱子即可.
要想使游戏一次性通关,则三个箱子要把右边的三个阴影位置占完,且每个箱子只能占一个位置;
观察三个箱子的位置,发现②号箱子会阻碍其余两个箱子的移动,因此要先推动②号箱子,其余两个箱子才能推动;然后推动①号箱子,最后推动③号箱子可以使得步数最少.
故答案为:②,①,③
【点评】本题考查平移变换,解答本题的关键要明确推箱子游戏的规则.
17.【分析】根据分式的加减将已知等式变形为,代入分式即可求解.
解:∵,
∴,
即,
∴
.
故答案为:.
【点评】本题考查了分式的求值,分式的加减,正确的计算是解题的关键.
18.【分析】用大矩形的面积减去小矩形的面积得出代数式,然后根据整式的混合运算法则进行计算即可.
解:根据题意可得剩余部分的面积为
,
故答案为:.
【点评】本题考查了整式的混合运算的应用,读懂题意,根据题意列出代数式,然后根据整式的混合运算法则进行计算是解本题的关键.
19.【分析】先根据乘方运算、绝对值的意义,算术平方根的运算化简,再进行加减运算即可.
.
【点评】本题考查了实数的混合运算,熟练掌握各个运算法则是解题的关键.
20.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
解:解不等式①,得:,
解不等式②,得:,
则不等式组的解集为.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
21.【分析】将变形得,将化简得,代入求解即可.
解:∵ ,
则 ,
,
原式,
,
将 代入得:
原式.
【点评】本题考查了已知式子的值求代数式的值,整式的化简求值,整体代入法;解题的关键是掌握整体代入法,并由已知式子的值得到.
22.【分析】(1)根据同位角相等,两直线平行,即可得出结论;
(2)先由平行线的性质得到∠1=∠3,又∠1=∠2,所以∠2=∠3,再次推出EF∥AD,即得到∠EFB=∠ADB,已知AD⊥BC于点D,故得到EF与BC的位置关系是垂直.
(1)DG∥BA,
∵∠CDG=∠B(已知),∴DG∥AB(同位角相等,两直线平行),
(2)EF⊥BC
∵∠1=∠3(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠2=∠3,
∴EF∥AD(内同位角相等,两直线平行),
∴∠EFB=∠ADB(两直线平行,同位角相等),
又AD⊥BC于点D(已知),
∴∠ADB=90°,
∴∠EFB=∠ADB=90°,
∴EF⊥CB.
【点评】考查的知识点是平行线的判定与性质,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
23.【分析】(1)设文学书的价格为x元,科普书的价格为元,根据所买的科普书比所买的文学书少1本列出方程,解方程即可得到答案;
(2)设购买文学书m本.根据用60元购买科普书和文学书两种书共10本列出不等式,解不等式,即可得到答案.
(1)解:设文学书的价格为x元,科普书的价格为元,
由题意得,,
解得:,
经检验是原分式方程的解,且符合题意,
则科普书的价格为:(元).
答:文学书的价格为5元,科普书的价格为元;
(2)设购买文学书m本.
则有,
解得,.
答:至少要购买文学书6本.
【点评】此题考查了分式方程和一元一次不等式的应用,根据题意正确列出分式方程和不等式是解题的关键.
24.【分析】(1)设每件甲产品的成本价为元,每件乙产品的成本价为元,根据“购进5件甲产品和8件乙产品需要成本170元,购进2件甲产品和4件乙产品需要成本80元”列得二元一次方程组,即可求解;
(2)设商店从批发商处购进甲产品件,则购进乙产品件,根据“购进甲、乙两种产品共100件,购进时总成本不超过1300元,且全部销售完以后利润不低于1580元”列得不等式组,即可求解.
(1)解:设每件甲产品的成本价为元,每件乙产品的成本价为元,
,
解之得:,
答:每件甲产品的成本价为10元,每件乙产品的成本价为15元;
(2)解:设商店从批发商处购进甲产品件,则购进乙产品件,
,
解之得:,
∵为整数,
∴,41,42,
答:有3种购进方案.
【点评】本题考查了二元一次方程组的应用、一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.
25.【分析】(1)根据资料提示的算法即可求解;
(2)分别按多项成乘法运算方法展开与,再根据资料提供的方法即可求解;
(3)根据分式的运算方法,计算,再根据资料提供的解题方法即可求解.
(1)解:,
,
∵,
∴,
故答案为:,.
(2)解:,
∵
又
∴.
(3)解:,当时,原式;
当时,
,
∵(当时,等号成立)
∴,
当时,的最大值为.
【点评】本题主要考查分式的运算,理解题干意思,掌握分式的混合运算是解题的关键.
26.【分析】(1)依据角平分线,可得∠AEM=∠FEM,根据∠FEM=∠FME,可得∠AEM=∠FME,进而得出ABCD;
(2)①依据平行线的性质可得∠AEG=120°,再根据EH平分∠FEG,EM平分∠AEF,即可得到∠MEH=∠AEG=60°,再根据HN⊥ME,即可得到Rt△EHN中,∠EHN=90°-65°=25°;
②分两种情况进行讨论:当点G在点F的右侧时,α=2β.当点G在点F的左侧时,α=180°-2β.
(1)
解:∵EM平分∠AEF,
∴∠AEM=∠FEM,
又∵∠FEM=∠FME,
∴∠AEM=∠FME,
∴ABCD;
(2)
解:①如图2,
∵ABCD,α=60°,
∴∠AEG=120°,
又∵EH平分∠FEG,EM平分∠AEF,
∴∠HEF=∠FEG,∠MEF=∠AEF,
∴∠MEH=∠AEG=60°,
又∵HN⊥ME,
∴Rt△EHN中,∠EHN=90°-60°=30°,
即β=30°;
②点G是射线MD上一动点,故分两种情况讨论:
如图2,当点G在点F的右侧时,α=2β.
证明:∵ABCD,
∴∠AEG=180°-α,
又∵EH平分∠FEG,EM平分∠AEF,
∴∠HEF=∠FEG,∠MEF=∠AEF,
∴∠MEH=∠AEG=(180°-α),
又∵HN⊥ME,
∴Rt△EHN中,∠EHN=90°-∠MEH=90°-(180°-α)=α,
即α=2β;
如图3,当点G在点F的左侧时,α=180°-2β.
证明:∵ABCD,
∴∠AEG=∠EGF=α,
又∵EH平分∠FEG,EM平分∠AEF,
∴∠HEF=∠FEG,∠MEF=∠AEF,
∴∠MEH=∠MEF-∠HEF
=(∠AEF-∠FEG)
=∠AEG
=α,
又∵HN⊥ME,
∴Rt△EHN中,∠EHN=90°-∠MEH,
即β=90°-α.即α=180°-2β.
综上所述 ,α=2β或α=180°-2β.
【点评】本题主要考查了平行线的性质与判定,角平分线的定义的运用,解决问题的关键是掌握:两直线平行,内错角相等;两直线平行,同旁内角互补;利用角的和差关系进行推算.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版2022-2023学年度下学期七年级期末练习数学试2
姓名:__________班级:__________考号:__________总分__________
一、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.下列式子正确的是( )
A. B. C. D.
2.下列四个实数中,最大的数是( )
A. B. C. D.
3.下列各式计算正确的是( )
A. B. C. D.
4.如图,直线,,则的度数是( )
A. B. C. D.
5.口味虾、臭豆腐、嗦螺和糖油粑粑是是长沙著名的小吃,某兴趣小组在班级发动了一项“舌尖上的长沙-我最喜欢的长沙小吃”调查活动,发现结果满足以下三个条件:
(1)喜欢嗦螺的人数少于喜欢口味虾的人数;
(2)喜欢嗦螺的人数多于喜欢臭豆腐的人数;
(3)喜欢臭豆腐的人数的3倍多于喜欢口味虾的人数.
若喜欢臭豆腐的人数为6,则喜欢嗦螺的人数的最大值为( )
A.16 B.6 C.17 D.7
6.用如图所示的正方形和长方形卡片若干张,拼成一个长为,宽为的长方形,需要类卡片( )张.
A.3 B.4 C.5 D.6
7.下列分式方程有解的是( )
A. B.
C. D.
8.如图:能判断的条件是( )
A. B. C. D.
9.若:,,,则:代数式的值等于( )
A. B. C. D.
10.多项式的公因式是( )
A. B. C. D.
11.下列判断正确的是( )
A.若x为有理数,则 B.若x为有理数,则
C.若,则 D.若,则
12.如果不等式的正整数解是1,2,3,那么的取值范围是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分)
13.若,,则___________________.
14.不等式组的解集为_____.
15.用“”定义一种新运算:对于任意有理数和,规定,若,则的值为___________.
16.庆庆是一位特别喜欢学习数学的小朋友,周末这天他做完作业,在手机上找了一款数学相关的益智类游戏《推箱子》,要求将图中编号为①②③的三个箱子分别推进图中“回”字的位置.如果庆庆要想一次性通关,且尽可能让自己步数少,应该先推( )号箱子,再推( )号箱子,最后推( )号箱子.
17.已知,则分式的值为______________.
18.如图,在长为,宽为的长方形铁片上,挖去长为,宽为的小长方形铁片,则剩余部分面积为______.
三、解答题(本大题共8小题,共78分)
19.计算:.
20.解不等式组:.
21.已知,求的值.
22.已知:如图,AD⊥BC于点D,∠1=∠2,∠CDG=∠B,
(1)能否得出DG∥BA?试说明理由.(2)EF与BC有什么关系?试说明理由.
23.小明和同学一起去书店买书,他们先用15元买了一种科普书,又用15元买了一种文学书.科普书的价格比文学书高出一半,因此他们所买的科普书比所买的文学书少1本.
(1)这种科普书和这种文学书的价格各是多少?
(2)若准备用60元购买科普书和文学书两种书共10本,则至少要购买文学书多少本?
24.某商店从批发商处购进甲、乙两种产品,购进5件甲产品和8件乙产品需要成本170元,购进2件甲产品和4件乙产品需要成本80元.销售时,每件甲产品售价为20元,每件乙产品售价为35元.
(1)求每件甲产品和每件乙产品的成本价;
(2)若商店从批发商处购进甲、乙两种产品共100件,购进时总成本不超过1300元,且全部销售完以后利润不低于1580元,请问有几种购进方案?
25.由完全平方差公式可知,,而,所以,对所有的实数都有:,且只有当时,才有等号成立:.
应用上面的结论解答下列问题:
(1)计算 ,由此可知 (填不等号);
(2)已知为不相等的两正数,试比较:与的大小;
(3)试求分式的最大值.
26.如图1,已知两条直线,被直线所截,分别交于点,点,平分交于点,且.
(1)判断直线与直线是否平行,并说明理由;
(2)如图2,点是射线上一动点(不与点,重合),平分交于点,过点作于点,设,.
①当点在点的右侧时,若,求的度数;
②当点在运动过程中,与之间有怎样的数量关系?请写出你的猜想,并加以证明
参考答案:
1.【分析】分别根据合并同类项法则,幂的乘方运算法则,同底数幂的乘法法则以及完全平方公式逐一判断即可.
解:A、,故本选项符合题意;
B、,故本选项不合题意;
C、与不是同类项,所以不能合并,故本选项不合题意;
D、,故本选项不合题意;
故选:A.
【点评】本题主要考查了同底数幂的乘法,合并同类项,完全平方公式以及幂的乘方,熟记相关公式与运算法则是解答本题的关键.
2.【分析】根据实数的大小比较即可求解.
解: ∵ ,
∴这四个实数中,最大的数是,
故选:C.
【点评】本题考查了实数的大小比较法则,熟练掌握实数的大小比较法则是解题关键.
3.【分析】根据算术平方根,零指数幂,负整数指数幂,合并同类项,化简绝对值,逐项分析判断即可求解.
解:A. ,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项正确,符合题意;
D. ,故该选项不正确,不符合题意;
故选:C.
【点评】本题考查了算术平方根,零指数幂,负整数指数幂,合并同类项,化简绝对值,熟练掌握算术平方根,零指数幂,负整数指数幂,合并同类项,化简绝对值是解题的关键.
4.【分析】根据平行线的性质可得,再根据,即可得到答案.
解:如图所示,
,
,,
,
,
,
故选:A.
【点评】本题主要考查了平行线的性质、互补的定义,熟练掌握两直线平行,同位角相等,是解题的关键.
5.【分析】设喜欢嗦螺的人数是x,喜欢口味虾的人数是y,根据题意列出不等式组即可解答.
设喜欢嗦螺的人数是x,喜欢口味虾的人数是y,
根据喜欢臭豆腐的人数是6人,
结合题意有:,且x和y都是正整数,
解得:,且x和y都是正整数,
即喜欢口味虾的人数最多为17人,则喜欢嗦螺的人数最多为16人,
故选:A.
【点评】本题考查了不等式组的应用,根据题意列出不等式组是解答本题的关键.
6.【分析】根据长方形的面积公式即可得出结果.
解:∵ 长方形长为,宽为
∴长方形的面积:
∴需要B内卡片5张.
故选C.
【点评】本题考查多项式的乘法,灵活运用多项式乘法法则和数形结合思想是解题的关键.
7.【分析】分别解分式方程,即可求解.
解:A.
方程两边同时乘以得,
解得:,
经检验是原方程的增根,则原方程无解;故该选项不正确,不符合题意;
B. ,方程两边同时乘以,得,
∵,
∴原方程无解;故该选项不正确,不符合题意;
C. ,去分母得,不成立,
∴原方程无解;故该选项不正确,不符合题意;
D. ,去分母得,解得:,
经检验,是原方程的解,故该选项正确,符合题意;
故选:D.
【点评】本题考查了解分式方程,熟练掌握解分式方程的步骤是解题的关键.
8.【分析】根据平行线的判定方法对各选项进行判断.
解:A.当时,根据内错角相等,两直线平行,可以判定,故A符合题意;
B.当时,无法判断,故B不符合题意;
C.当时,无法判断,故C不符合题意;
D.当时,无法判断,故D不符合题意.
故答案选:A.
【点评】本题考查了平行线的判定,解题的关键是熟练掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
9.【分析】首先根据题意,联立方程组,得出,用字母表示出、的值,然后把、的值代入代数式,计算即可得出结果.
解:∵,,
∴,
由,可得:,
把代入,可得:,
又∵,
∴
.
故选:D
【点评】本题考查了二元一次方程组的解法、分式的化简求值,解本题的关键在根据已知二元一次方程组进行消元,将分式中的三个未知数化成只含一个未知数的式子表示.
10.【分析】根据多项式的公因式的确定方法,即可求解.
解:多项式的公因式是,
故选C.
【点评】本题考查了公因式的定义.确定多项式中各项的公因式,可概括为三“定”:①定系数,即确定各项系数的最大公约数;②定字母,即确定各项的相同字母因式(或相同多项式因式);③定指数,即各项相同字母因式(或相同多项式因式)的指数的最低次幂.
11.【分析】根据不等式的基本性质判断即可.
解:,,
,
A错误;
,,
,
C错误;
,,
D错误;
∵,
∴,即成立,
∴B选项正确,
故选B.
【点评】本题考查了不等式的基本性质,熟练运用不等式的基本性质是解题关键.
12.【分析】先求出不等式的解集,再根据其正整数解列出不等式,解此不等式即可求解.
解:解不等式得到:,
正整数解为,,,
,
解得.
故选:.
【点评】本题考查了一元一次不等式的整数解,根据的取值范围正确确定的范围是解题的关键.再解不等式时要根据不等式的基本性质.
13.【分析】将变形为即可求解.
解:,
.
故答案为:
【点评】本题考查求一个数的算术平方根,将变形为是解题的关键.
14.【分析】分别解出每个不等式,再根据“同大取大,同小取小,大小小大中间找,大大小小找不到”确定公共解集即可.
解:
解不等式①,得:,
解不等式②,得:,
∴原不等式组的解集为.
故答案为:.
【点评】本题考查解一元一次不等式组.掌握求不等式组解集的口诀“同大取大,同小取小,大小小大中间找,大大小小找不到”是解题关键.
15.【分析】根据题目中的新定义,理解公式并利用公式将已知条件转化为方程,最后得出结论.
解:∵,
∴,
∵,
∴,
∴,
∴经检验:是分式方程的解,
故答案为:.
【点评】本题有理数的混合运算,解分式方程,注意检验,解答本题的关键是根据新运算列出方程.
16.【分析】要一次性通关,先推阻碍其它箱子的箱子,然后推动其它箱子即可.
要想使游戏一次性通关,则三个箱子要把右边的三个阴影位置占完,且每个箱子只能占一个位置;
观察三个箱子的位置,发现②号箱子会阻碍其余两个箱子的移动,因此要先推动②号箱子,其余两个箱子才能推动;然后推动①号箱子,最后推动③号箱子可以使得步数最少.
故答案为:②,①,③
【点评】本题考查平移变换,解答本题的关键要明确推箱子游戏的规则.
17.【分析】根据分式的加减将已知等式变形为,代入分式即可求解.
解:∵,
∴,
即,
∴
.
故答案为:.
【点评】本题考查了分式的求值,分式的加减,正确的计算是解题的关键.
18.【分析】用大矩形的面积减去小矩形的面积得出代数式,然后根据整式的混合运算法则进行计算即可.
解:根据题意可得剩余部分的面积为
,
故答案为:.
【点评】本题考查了整式的混合运算的应用,读懂题意,根据题意列出代数式,然后根据整式的混合运算法则进行计算是解本题的关键.
19.【分析】先根据乘方运算、绝对值的意义,算术平方根的运算化简,再进行加减运算即可.
.
【点评】本题考查了实数的混合运算,熟练掌握各个运算法则是解题的关键.
20.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
解:解不等式①,得:,
解不等式②,得:,
则不等式组的解集为.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
21.【分析】将变形得,将化简得,代入求解即可.
解:∵ ,
则 ,
,
原式,
,
将 代入得:
原式.
【点评】本题考查了已知式子的值求代数式的值,整式的化简求值,整体代入法;解题的关键是掌握整体代入法,并由已知式子的值得到.
22.【分析】(1)根据同位角相等,两直线平行,即可得出结论;
(2)先由平行线的性质得到∠1=∠3,又∠1=∠2,所以∠2=∠3,再次推出EF∥AD,即得到∠EFB=∠ADB,已知AD⊥BC于点D,故得到EF与BC的位置关系是垂直.
(1)DG∥BA,
∵∠CDG=∠B(已知),∴DG∥AB(同位角相等,两直线平行),
(2)EF⊥BC
∵∠1=∠3(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠2=∠3,
∴EF∥AD(内同位角相等,两直线平行),
∴∠EFB=∠ADB(两直线平行,同位角相等),
又AD⊥BC于点D(已知),
∴∠ADB=90°,
∴∠EFB=∠ADB=90°,
∴EF⊥CB.
【点评】考查的知识点是平行线的判定与性质,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
23.【分析】(1)设文学书的价格为x元,科普书的价格为元,根据所买的科普书比所买的文学书少1本列出方程,解方程即可得到答案;
(2)设购买文学书m本.根据用60元购买科普书和文学书两种书共10本列出不等式,解不等式,即可得到答案.
(1)解:设文学书的价格为x元,科普书的价格为元,
由题意得,,
解得:,
经检验是原分式方程的解,且符合题意,
则科普书的价格为:(元).
答:文学书的价格为5元,科普书的价格为元;
(2)设购买文学书m本.
则有,
解得,.
答:至少要购买文学书6本.
【点评】此题考查了分式方程和一元一次不等式的应用,根据题意正确列出分式方程和不等式是解题的关键.
24.【分析】(1)设每件甲产品的成本价为元,每件乙产品的成本价为元,根据“购进5件甲产品和8件乙产品需要成本170元,购进2件甲产品和4件乙产品需要成本80元”列得二元一次方程组,即可求解;
(2)设商店从批发商处购进甲产品件,则购进乙产品件,根据“购进甲、乙两种产品共100件,购进时总成本不超过1300元,且全部销售完以后利润不低于1580元”列得不等式组,即可求解.
(1)解:设每件甲产品的成本价为元,每件乙产品的成本价为元,
,
解之得:,
答:每件甲产品的成本价为10元,每件乙产品的成本价为15元;
(2)解:设商店从批发商处购进甲产品件,则购进乙产品件,
,
解之得:,
∵为整数,
∴,41,42,
答:有3种购进方案.
【点评】本题考查了二元一次方程组的应用、一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.
25.【分析】(1)根据资料提示的算法即可求解;
(2)分别按多项成乘法运算方法展开与,再根据资料提供的方法即可求解;
(3)根据分式的运算方法,计算,再根据资料提供的解题方法即可求解.
(1)解:,
,
∵,
∴,
故答案为:,.
(2)解:,
∵
又
∴.
(3)解:,当时,原式;
当时,
,
∵(当时,等号成立)
∴,
当时,的最大值为.
【点评】本题主要考查分式的运算,理解题干意思,掌握分式的混合运算是解题的关键.
26.【分析】(1)依据角平分线,可得∠AEM=∠FEM,根据∠FEM=∠FME,可得∠AEM=∠FME,进而得出ABCD;
(2)①依据平行线的性质可得∠AEG=120°,再根据EH平分∠FEG,EM平分∠AEF,即可得到∠MEH=∠AEG=60°,再根据HN⊥ME,即可得到Rt△EHN中,∠EHN=90°-65°=25°;
②分两种情况进行讨论:当点G在点F的右侧时,α=2β.当点G在点F的左侧时,α=180°-2β.
(1)
解:∵EM平分∠AEF,
∴∠AEM=∠FEM,
又∵∠FEM=∠FME,
∴∠AEM=∠FME,
∴ABCD;
(2)
解:①如图2,
∵ABCD,α=60°,
∴∠AEG=120°,
又∵EH平分∠FEG,EM平分∠AEF,
∴∠HEF=∠FEG,∠MEF=∠AEF,
∴∠MEH=∠AEG=60°,
又∵HN⊥ME,
∴Rt△EHN中,∠EHN=90°-60°=30°,
即β=30°;
②点G是射线MD上一动点,故分两种情况讨论:
如图2,当点G在点F的右侧时,α=2β.
证明:∵ABCD,
∴∠AEG=180°-α,
又∵EH平分∠FEG,EM平分∠AEF,
∴∠HEF=∠FEG,∠MEF=∠AEF,
∴∠MEH=∠AEG=(180°-α),
又∵HN⊥ME,
∴Rt△EHN中,∠EHN=90°-∠MEH=90°-(180°-α)=α,
即α=2β;
如图3,当点G在点F的左侧时,α=180°-2β.
证明:∵ABCD,
∴∠AEG=∠EGF=α,
又∵EH平分∠FEG,EM平分∠AEF,
∴∠HEF=∠FEG,∠MEF=∠AEF,
∴∠MEH=∠MEF-∠HEF
=(∠AEF-∠FEG)
=∠AEG
=α,
又∵HN⊥ME,
∴Rt△EHN中,∠EHN=90°-∠MEH,
即β=90°-α.即α=180°-2β.
综上所述 ,α=2β或α=180°-2β.
【点评】本题主要考查了平行线的性质与判定,角平分线的定义的运用,解决问题的关键是掌握:两直线平行,内错角相等;两直线平行,同旁内角互补;利用角的和差关系进行推算.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
