【全程复习方略】高中数学 均匀随机数的产生课时提能训练 新人教A版必修3
文档属性
| 名称 | 【全程复习方略】高中数学 均匀随机数的产生课时提能训练 新人教A版必修3 |
|
|
| 格式 | zip | ||
| 文件大小 | 120.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-18 14:57:30 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
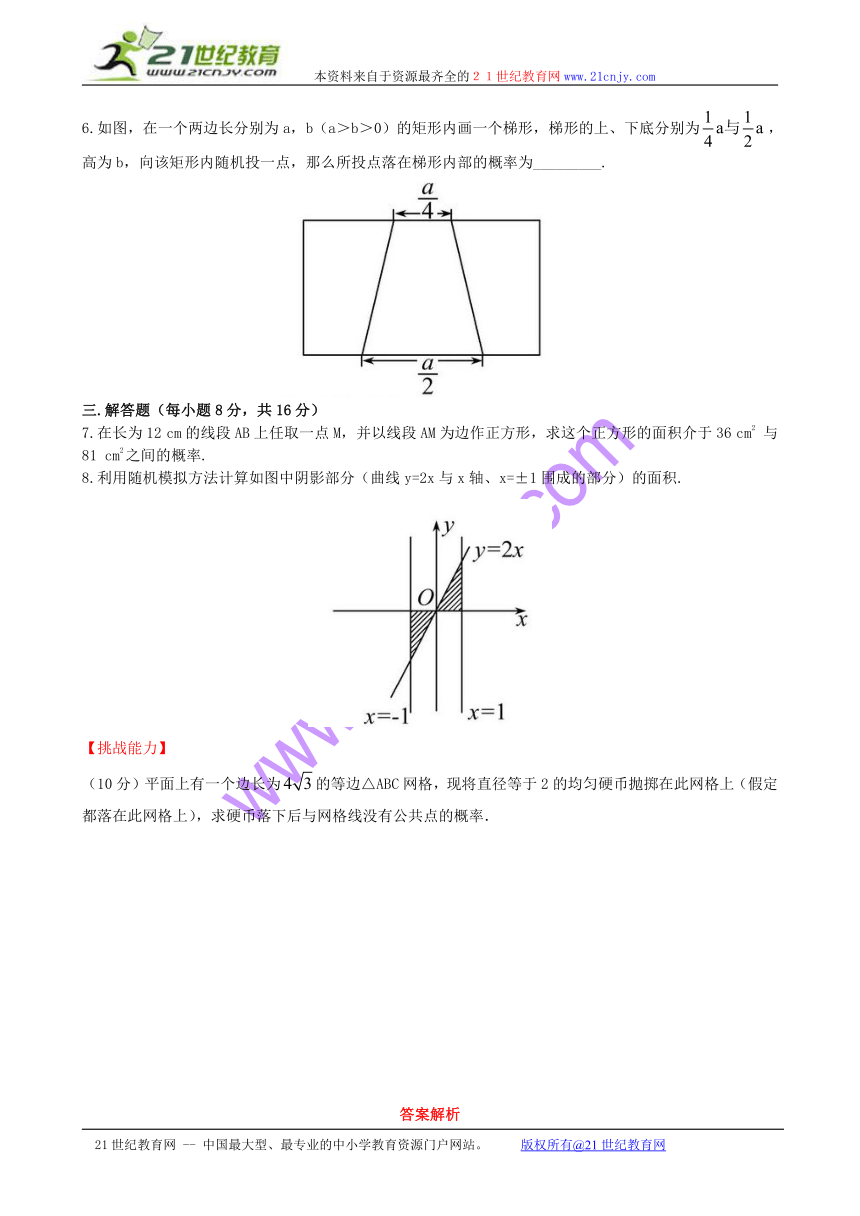
均匀随机数的产生课时提能训练
(30分钟50分)
一、选择题(每小题4分,共16分)
1.设一直角三角形两直角边的长均是区间[0,1]上的随机数,则斜边的长小于1的概率为( )
2.欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为1.5 cm的圆,中间有边长为0.5 cm的正方形孔,若你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率为( )
3.(2012·海口高一检测)同时转动如 ( http: / / www.21cnjy.com )图所示的两个转盘,记转盘甲得到的数为x,转盘乙得到的数为y,构成数对(x,y),则所有数对(x,y)中满足xy=4的概率为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
4.(易错题)如图,在△AOB中,已知∠A ( http: / / www.21cnjy.com )OB=60°,OA=2,OB=5,在线段OB上任取一点C,求△AOC为钝角三角形的概率.( )www-2-1-cnjy-com
( http: / / www.21cnjy.com )
(A)0.6 (B)0.4 (C)0.2 (D)0.1
二、填空题(每小题4分,共8分)
5.如图,矩形的长为6,宽为3,在矩形内随 ( http: / / www.21cnjy.com )机地撒300颗黄豆,数得落在阴影部分的黄豆为125颗,则我们可以估计出阴影部分的面积约为__________. 21*cnjy*com
( http: / / www.21cnjy.com )
6.如图,在一个两边长分别为a,b(a>b>0)的矩形内画一个梯形,梯形的上、下底分别为,高为b,向该矩形内随机投一点,那么所投点落在梯形内部的概率为_________.【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
三.解答题(每小题8分,共16分)
7.在长为12 cm的线段AB上任取一点M,并以线段AM为边作正方形,求这个正方形的面积介于36 cm2 与81 cm2之间的概率.2·1·c·n·j·y
8.利用随机模拟方法计算如图中阴影部分(曲线y=2x与x轴、x=±1围成的部分)的面积.
( http: / / www.21cnjy.com )
【挑战能力】
(10分)平面上有一个边长为的等边△ABC网格,现将直径等于2的均匀硬币抛掷在此网格上(假定都落在此网格上),求硬币落下后与网格线没有公共点的概率.【出处:21教育名师】
答案解析
1.【解析】选C.设两直角边分别为x,y,则x,y满足x∈[0,1],y∈[0,1],则
2.【解析】选A.由题意所求的概率为
3.【解析】选C.数对(x,y)共有4×4=16个,其中满足xy=4的有(1,4),(4,1),(2,2),3个.故所求概率.21世纪教育网版权所有
4.【解题指南】试验发生包 ( http: / / www.21cnjy.com )含的事件对应的是长度为5的一条线段,满足条件的事件是组成钝角三角形,包括两种情况,第一种∠ACO为钝角,第二种∠OAC为钝角,根据等可能事件的概率得到结果.
【解析】选B.试验发生包含的事件对应的是长度为5的一条线段,满足条件的事件是组成钝角三角形,包括两种情况:21教育网
第一种∠ACO为钝角,这种情况的边界是∠ACO=90°的时候,此时OC=1,∴这种情况下,满足要求的是0<OC<1.21·cn·jy·com
第二种∠OAC为钝角,这种情况的边界是∠OAC=90°的时候,此时OC=4,∴这种情况下,满足要求的是4<OC<5.21·世纪*教育网
综合两种情况,若△AOC为钝角三角形,则0<OC<1或4<OC<5.∴概率.
【误区警示】本题易出现只考虑一种情况的错误,致使所得结果为0.2.
5.【解析】∵矩形的长为6,宽为3,则,
答案:
6.【解析】∵图中梯形的面积为
矩形的面积为S=ab,
∴落在梯形内部的概率为:
答案:
7.【解题指南】正方形的面积只与边长有 ( http: / / www.21cnjy.com )关,此题可以转化为在12 cm长的线段AB上任取一点M,求使得AM的长度介于6 cm与9 cm之间的概率.2-1-c-n-j-y
【解析】(1)用计算机产生一组 [0,1]内均匀随机数a1=RAND;
(2)经过伸缩变换,a=a1*12,得到 [0,12]内的均匀随机数;
(3)统计试验总次数N和 [6,9]内随机数个数N1;
(4)计算频率
记事件A={面积介于36 cm2与81 cm2之间}={长度介于6 cm与9 cm之间},则
P(A)的近似值为fn(A)=
8.【解析】(1)利用计算机产生两组[0,1]上的均匀随机数,a1=RAND,b1=RAND.
(2)经过平移和伸缩变换,a=(a1-0.5)*2,b=b1*2,得到一组[-1,1]上的均匀随机数和一组[0,2]上的均匀随机数.21cnjy.com
(3)统计试验总次数N和落在阴影内的点数N1.
(4)计算频率即为点落在阴影部分的概率的近似值.
(5)用几何概型的概率公式求得点落在阴影部分的概率为,即为阴影部分的面积值.
【挑战能力】
【解析】设事件M={硬币落下后与等边△ABC的网格线没有公共点}.
要使硬币落在网格上的条件是硬币的重心需落在此△ABC的边上或内部,
故所有的随机基本事件所构成的区域为△ABC.
当硬币与边恰有一个公共点的重心位置就是临界点的位置.
如图,所有临界点形成三条临界线,三条临界线构成一个小△EFG区域,因此事件M所构成的区域为△EFG区域.www.21-cn-jy.com
经计算得△EFG的边长为.
.
( http: / / www.21cnjy.com )
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
均匀随机数的产生课时提能训练
(30分钟50分)
一、选择题(每小题4分,共16分)
1.设一直角三角形两直角边的长均是区间[0,1]上的随机数,则斜边的长小于1的概率为( )
2.欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为1.5 cm的圆,中间有边长为0.5 cm的正方形孔,若你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率为( )
3.(2012·海口高一检测)同时转动如 ( http: / / www.21cnjy.com )图所示的两个转盘,记转盘甲得到的数为x,转盘乙得到的数为y,构成数对(x,y),则所有数对(x,y)中满足xy=4的概率为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
4.(易错题)如图,在△AOB中,已知∠A ( http: / / www.21cnjy.com )OB=60°,OA=2,OB=5,在线段OB上任取一点C,求△AOC为钝角三角形的概率.( )www-2-1-cnjy-com
( http: / / www.21cnjy.com )
(A)0.6 (B)0.4 (C)0.2 (D)0.1
二、填空题(每小题4分,共8分)
5.如图,矩形的长为6,宽为3,在矩形内随 ( http: / / www.21cnjy.com )机地撒300颗黄豆,数得落在阴影部分的黄豆为125颗,则我们可以估计出阴影部分的面积约为__________. 21*cnjy*com
( http: / / www.21cnjy.com )
6.如图,在一个两边长分别为a,b(a>b>0)的矩形内画一个梯形,梯形的上、下底分别为,高为b,向该矩形内随机投一点,那么所投点落在梯形内部的概率为_________.【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
三.解答题(每小题8分,共16分)
7.在长为12 cm的线段AB上任取一点M,并以线段AM为边作正方形,求这个正方形的面积介于36 cm2 与81 cm2之间的概率.2·1·c·n·j·y
8.利用随机模拟方法计算如图中阴影部分(曲线y=2x与x轴、x=±1围成的部分)的面积.
( http: / / www.21cnjy.com )
【挑战能力】
(10分)平面上有一个边长为的等边△ABC网格,现将直径等于2的均匀硬币抛掷在此网格上(假定都落在此网格上),求硬币落下后与网格线没有公共点的概率.【出处:21教育名师】
答案解析
1.【解析】选C.设两直角边分别为x,y,则x,y满足x∈[0,1],y∈[0,1],则
2.【解析】选A.由题意所求的概率为
3.【解析】选C.数对(x,y)共有4×4=16个,其中满足xy=4的有(1,4),(4,1),(2,2),3个.故所求概率.21世纪教育网版权所有
4.【解题指南】试验发生包 ( http: / / www.21cnjy.com )含的事件对应的是长度为5的一条线段,满足条件的事件是组成钝角三角形,包括两种情况,第一种∠ACO为钝角,第二种∠OAC为钝角,根据等可能事件的概率得到结果.
【解析】选B.试验发生包含的事件对应的是长度为5的一条线段,满足条件的事件是组成钝角三角形,包括两种情况:21教育网
第一种∠ACO为钝角,这种情况的边界是∠ACO=90°的时候,此时OC=1,∴这种情况下,满足要求的是0<OC<1.21·cn·jy·com
第二种∠OAC为钝角,这种情况的边界是∠OAC=90°的时候,此时OC=4,∴这种情况下,满足要求的是4<OC<5.21·世纪*教育网
综合两种情况,若△AOC为钝角三角形,则0<OC<1或4<OC<5.∴概率.
【误区警示】本题易出现只考虑一种情况的错误,致使所得结果为0.2.
5.【解析】∵矩形的长为6,宽为3,则,
答案:
6.【解析】∵图中梯形的面积为
矩形的面积为S=ab,
∴落在梯形内部的概率为:
答案:
7.【解题指南】正方形的面积只与边长有 ( http: / / www.21cnjy.com )关,此题可以转化为在12 cm长的线段AB上任取一点M,求使得AM的长度介于6 cm与9 cm之间的概率.2-1-c-n-j-y
【解析】(1)用计算机产生一组 [0,1]内均匀随机数a1=RAND;
(2)经过伸缩变换,a=a1*12,得到 [0,12]内的均匀随机数;
(3)统计试验总次数N和 [6,9]内随机数个数N1;
(4)计算频率
记事件A={面积介于36 cm2与81 cm2之间}={长度介于6 cm与9 cm之间},则
P(A)的近似值为fn(A)=
8.【解析】(1)利用计算机产生两组[0,1]上的均匀随机数,a1=RAND,b1=RAND.
(2)经过平移和伸缩变换,a=(a1-0.5)*2,b=b1*2,得到一组[-1,1]上的均匀随机数和一组[0,2]上的均匀随机数.21cnjy.com
(3)统计试验总次数N和落在阴影内的点数N1.
(4)计算频率即为点落在阴影部分的概率的近似值.
(5)用几何概型的概率公式求得点落在阴影部分的概率为,即为阴影部分的面积值.
【挑战能力】
【解析】设事件M={硬币落下后与等边△ABC的网格线没有公共点}.
要使硬币落在网格上的条件是硬币的重心需落在此△ABC的边上或内部,
故所有的随机基本事件所构成的区域为△ABC.
当硬币与边恰有一个公共点的重心位置就是临界点的位置.
如图,所有临界点形成三条临界线,三条临界线构成一个小△EFG区域,因此事件M所构成的区域为△EFG区域.www.21-cn-jy.com
经计算得△EFG的边长为.
.
( http: / / www.21cnjy.com )
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
