第22章 二次函数导学案
文档属性
| 名称 | 第22章 二次函数导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 370.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-17 13:29:36 | ||
图片预览



文档简介
课题 22.1.1 二次函数 课时 1课时 课型 新授课
学习目标 1. 知道二次函数的有关概念.2. 会确定二次函数关系式中各项的系数。3. 确定实际问题中二次函数的关系式。
重点 知道二次函数中的有关概念,能列出实际问题中二次函数解析式
难点 能列出实际问题中二次函数解析式
导学流程
【旧知回顾】------不练不讲1.若在一个变化过程中有两个变量x和y, ( http: / / www.21cnjy.com )如果对于x的每一个值, y都有唯一的值与它对应,那么就说y是x的 ,x叫做 。2. 形如的函数是一次函数,当时,它是 函数。【自主预习】------不议不讲预习课本28页-29页内容一、探究新知1.若正方体的棱长为x,表面积为y,则y与x之间的函数关系式为 。2. n支球队参加比赛,每两队之间进行一场比赛.写出比赛的场次数m与球队数n之间的关系式_______________________.3. 某产品现有年产量20t,计划今后两 ( http: / / www.21cnjy.com )年增加产量。若每年都比上一年的产量增加x倍,两年后的产量为y,y与x之间的关系式为 。 4. 观察上述1、2、3中函数关系式有哪些共同之处? 。二、总结归纳:一般地,形如 ,( )的函数为二次函数。其中是自变量,是__________,b是___________,c是_____________.三、合作交流:(1)二次项系数为什么不等于0?答: 。(2)一次项系数和常数项可以为0吗?答: .【当堂检测】1.观察:①;②;③y=200x2+400x+200;④;⑤;⑥,这六个式子中二次函数有 。(只填序号)2. 是二次函数,则m的值为______________.3. 若物体运动的路段s(米)与时间t(秒)之间的关系为,则当t=4秒时,该物体所经过的路程为 。【作业布置】课本 第41页 第一、二题
课题 22.1.2 二次函数的图象和性质 课时 1课时 课型 新授课
学习目标 1.知道二次函数的图象是一条抛物线;2.会画二次函数y=ax2的图象;3.知道二次函数y=ax2的性质,并会灵活应用.
重点 知道二次函数y=ax2的性质,并会灵活应用
难点 知道二次函数y=ax2的性质,并会灵活应用。
考点 知道二次函数y=ax2的性质,并会灵活应用
导学流程
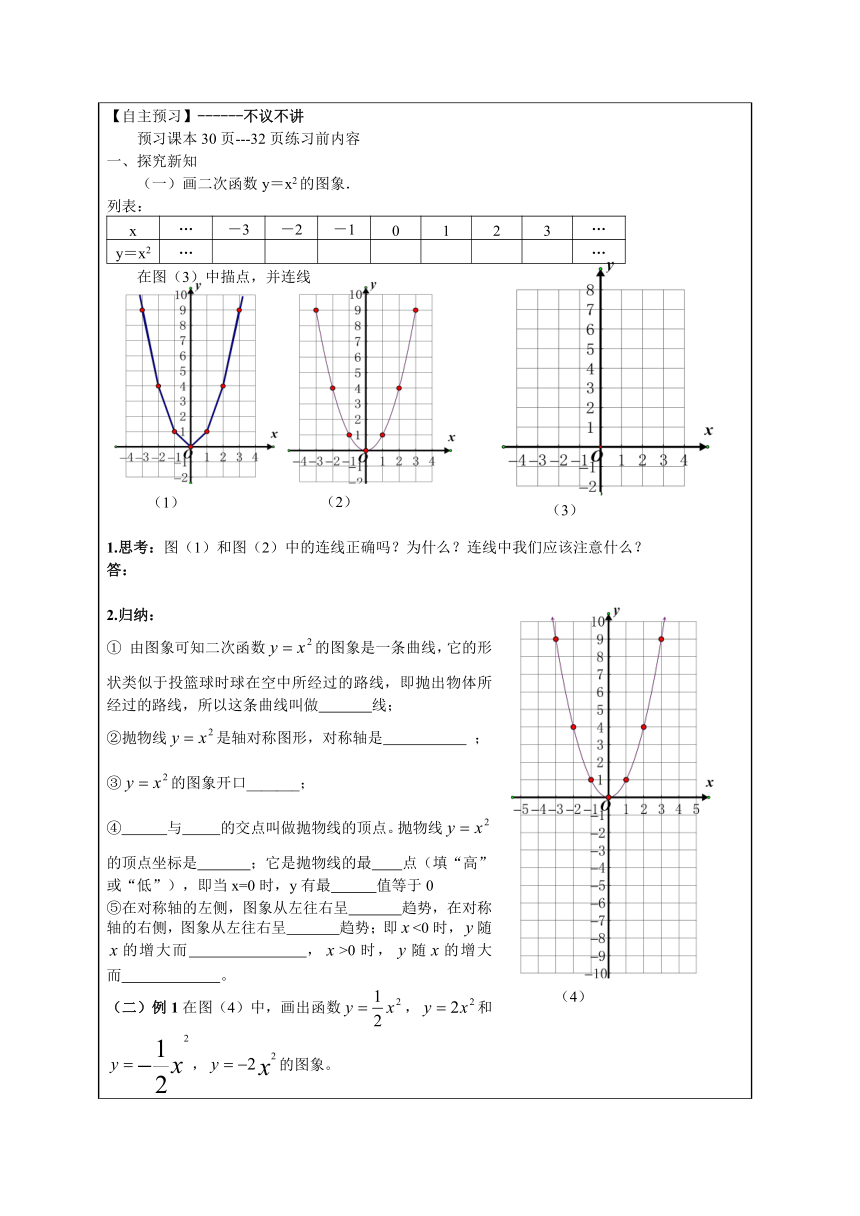
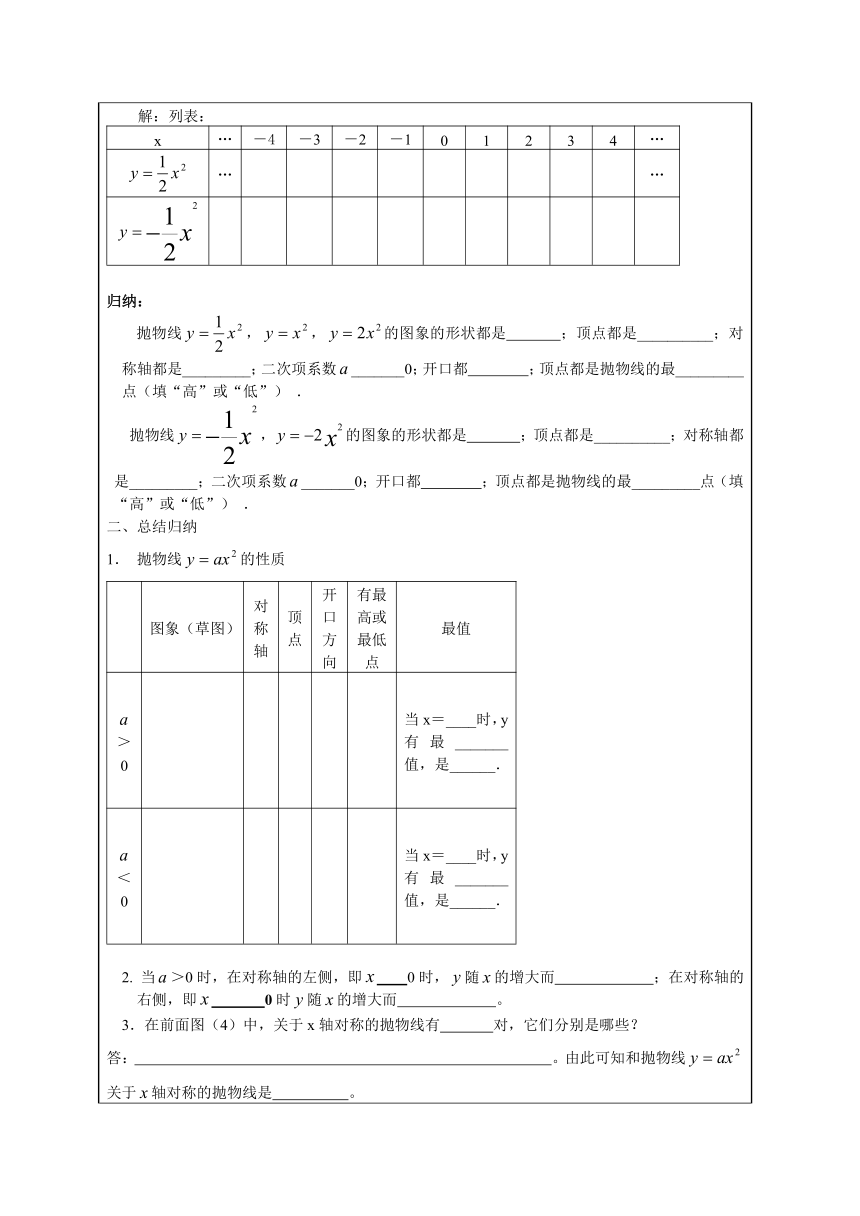
【旧知回顾】------不练不讲1描点法画一个函数图象的一般过程是① ;② ;③ 。2.一次函数图象的形状是 ;一次函数有那些性质呢?【自主预习】------不议不讲预习课本30页---32页练习前内容一、探究新知 (一)画二次函数y=x2的图象.列表:x…-3-2-10123…y=x2……在图(3)中描点,并连线1.思考:图(1)和图(2)中的连线正确吗?为什么?连线中我们应该注意什么?答:2.归纳:① 由图象可知二次函数的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,即抛出物体所经过的路线,所以这条曲线叫做 线;②抛物线是轴对称图形,对称轴是 ;③的图象开口_______;④ 与 的交点叫做抛物线的顶点。抛物线的顶点坐标是 ;它是抛物线的最 点(填“高”或“低”),即当x=0时,y有最 值等于0⑤在对称轴的左侧,图象从左往右呈 趋势,在对称轴的右侧,图象从左往右呈 趋势;即<0时,随的增大而 ,>0时,随的增大而 。(二)例1在图(4)中,画出函数,和,的图象。解:列表:x…-4-3-2-101234………归纳:抛物线,,的图象的形状都是 ;顶点都是__________;对称轴都是_________;二次项系数_______0;开口都 ;顶点都是抛物线的最_________点(填“高”或“低”) .抛物线,的图象的形状都是 ;顶点都是__________;对称轴都是_________;二次项系数_______0;开口都 ;顶点都是抛物线的最_________点(填“高”或“低”) .二、总结归纳1. 抛物线的性质图象(草图)对称轴顶点开口方向有最高或最低点最值>0当x=____时,y有最_______值,是______.<0当x=____时,y有最_______值,是______.2. 当>0时,在对称轴的左侧,即 0时,随的增大而 ;在对称轴的右侧,即 0时随的增大而 。3.在前面图(4)中,关于x轴对称的抛物线有 对,它们分别是哪些?答: 。由此可知和抛物线关于轴对称的抛物线是 。当>0时,越大,抛物线的开口越___________;当<0时, 越大,抛物线的开口越_________;因此,越大,抛物线的开口越________。【当堂检测】1.函数的图象顶点是__________,对称轴是________,开口向_______,当x=___________时,有最_________值是_________.2. 二次函数的图象开口向下,则m___________.3. 二次函数y=mx有最高点,则m=___________.4. 二次函数y=(k+1)x2的图象如图所示,则k的取值范围为___________.5.若二次函数的图象过点(1,-2),则的值是___________.6.如图,抛物线①② ③④ 开口从小到大排列是___________________________________;(只填序号)其中关于轴对称的两条抛物线是 和 。7.点A(,b)是抛物线上的一点,则b= ;过点A作x轴的平行线交抛物线另一点B的坐标是 。8..二次函数与直线交于点P(1,b).(1)求a、b的值;(2)写出二次函数的关系式,并指出x取何值时,该函数的y随x的增大而减小.【作业布置】 课本第41页第三、四题
课题 22.1.3二次函数的图象和性质(一) 课时 1课时 课型 新授课
学习目标 1.知道二次函数与的联系.2. 知道二次函数的性质,并会应用;
重点 知道二次函数的性质,并会应用
难点 知道二次函数的性质,并会应用
考点 知道二次函数的性质,并会应用
导学流程
【知识链接】------不练不讲1.直线可以看做是由直线 得到的。2.若一个一次函数的图象是由平移得到,并且过点(-1,3),求这个函数的解析式。由此你能推测二次函数与的图象之间又有何关系吗?猜想: 。【自主预习】------不议不讲预习32页—33页练习前内容探究新知 在同一直角坐标系中,画出二次函数,,的图象.解:列表、x…-3-2-10123…………… 描点、连线二、总结归纳:1.填表开口方向顶点对称轴有最高(低)点增减性可以发现,把抛物线向______平移______个单位,就得到抛物线; 把抛物线向_______平移______个单位,就得到抛物线.3.抛物线,,的形状_____________.开口大小相同。三、知识梳理:(一)抛物线特点:1.当时,开口向 ;当时,开口 ;2. 顶点坐标是 ;3. 对称轴是 。(二)抛物线与形状相同,位置不同,是由 平移得到的。(填上下或左右)二次函数图象的平移规律:上 下 。(三)的正负决定开口的 ;决定开口的 ,即不变,则抛物线的形 状 。因为平移没有改变抛物线的开口方向和形状,所以平移前后的两条抛物线值 。【当堂检测】1.抛物线向上平移3个单位,就得到抛物线__________________; 抛物线向下平移4个单位,就得到抛物线__________________.抛物线向上平移3个单位后的解析式为 , 它们的形状__________,当= 时,有最 值是 。由抛物线向垂直方向平移,且经过(1,7)点的抛物线的解析式是 , 是把原抛物线向 平移 个单位得到的。4. 写出一个顶点坐标为(0,-3),开口方向与抛物线的方向相反,形状相同的抛物线解析式____________________________.5. 抛物线关于x轴对称的抛物线解析式为______________________.6.二次函数的经过点A(1,-1)、B(2,5).⑴求该函数的表达式;⑵若点C(-2,),D(,7)也在函数图像上,求、的值。【作业布置】 课本P41第五题(1)
课题 22.1.3 二次函数的图象(二) 课时 2课时 课型 新授课
学习目标 1.会画二次函数的图象;2.知道二次函数与的联系.3. 知道二次函数的性质,并会应用
重点 知道二次函数的性质,并会应用
难点 知道二次函数的性质,并会应用
考点 知道二次函数的性质,并会应用
导学流程
【旧知回顾】------不练不讲1.将二次函数的图象向上平移2个单位,所得图象的解析式为 。2.将抛物线的图象向下平移3个单位后的抛物线的解析式为 。【自主预习】------不议不讲预习33页---35页练习前内容探究新知 画出二次函数,的图象;解: 先列表:…-4-3-2-101234……………描点、连线二、总结归纳:(1)的开口向 ,对称轴是直线 ,顶点坐标是 。图象有最 点,即= 时,有最 值是 ;在对称轴的左侧,即 时,随的增大而 ;在对称轴的右侧,即 时,随的增大而 。 可以看作由向 平移 个单位形成的。(2)的开口向 ,对称轴是直线 ,顶点坐标是 , 图象有最 点,即= 时,有最 值是 ;在对称轴的左侧,即 时,随的增大而 ;在对称轴的右侧,即 时随的增大而 。可以看作由向 平移 个单位形成的。可以看作由向 平移 个单位形成的。三、知识梳理(一)抛物线特点:1.当时,开口向 ;当时,开口 ;2. 顶点坐标是 ;3. 对称轴是直线 。(二)抛物线与形状相同,位置不同, 是由 平移得到的。(填上下或左右) 由学案可知二次函数图象的平移规律:左 右 ,上 下 。(三)的正负决定开口的 ;决定开口的 ,即不变,则抛物线的形状 。 因为平移没有改变抛物线的开口方向和形状,所以平移前后的两条抛物线值 。(四)抛物线与的单调性 (相同或不同)。【当堂检测】抛物线的开口_______;顶点坐标为_________; 对称轴是直线_______;当 时,随的增大而减小; 当 时,随的增大而增大。抛物线的开口_______;顶点坐标为_________; 对称轴是直线_______;当 时,随的增大而减小; 当 时,随的增大而增大。3. 抛物线的开口_______;顶点坐标为_________;对称轴是_______;4.抛物线向右平移4个单位后,得到的抛物线的表达式为______________.5. 抛物线向左平移3个单位后,得到的抛物线的表达式为______________.6.将抛物线向右平移1个单位后,得到的抛物线解析式为__________.7.抛物线与y轴的交点坐标是_______,与x轴的交点坐标为________.8. 写出一个顶点是(5,0),形状、开口方向与抛物线都相同的二次函数解析式_______________【作业布置】 课本P41第五题(2)
课题 22.1.3二次函数的图象(三) 课时 1课时 课型 新授课
学习目标 1.会画二次函数的顶点式的图象;2.知道二次函数的性质;
重点 知道二次函数的性质
难点 知道二次函数的性质
考点 知道二次函数的性质
导学流程
【旧知回顾】------不练不讲1.将二次函数的图象向上平移2个单位,所得图象的解析式为 。2.将抛物线的图象向左平移3个单位后的抛物线的解析式为 。【自主预习】------不议不讲 预习35页—36页例4前内容探究新知 在右图中做出的图象:观察:1. 抛物线开口向 ;顶点坐标是 ;对称轴是直线 。2. 抛物线和的形状 ,位置 。(填“相同”或“不同”)3. 抛物线是由如何平移得到的?答: 。二、合作交流平移前后的两条抛物线值变化吗?为什么?答: 三、总结归纳:结合上图和课本第35页例3归纳:(一)抛物线的特点:1.当时,开口向 ;当时,开口 ;2. 顶点坐标是 ;3. 对称轴是直线 。(二)抛物线与形状 ,位置不同,是由平移得到的。二次函数图象的平移规律:左 右 ,上 下 。(三)平移前后的两条抛物线值 。【当堂检测】1.二次函数的图象可由的图象( )A.向左平移1个单位,再向下平移2个单位得到 B.向左平移1个单位,再向上平移2个单位得到C.向右平移1个单位,再向下平移2个单位得到 D.向右平移1个单位,再向上平移2个单位得到2.抛物线开口 ,顶点坐标是 ,对称轴是 ,当x= 时,y有最 值为 。3.若把函数的图象分别向下、向左移动2个单位,则得到的函数解析式为 。4. 顶点坐标为(-2,3),开口方向和大小与抛物线相同的解析式为( )A. B. C. D.一条抛物线的形状、开口方向与抛物线相同,对称轴和抛物线相同,且顶点纵坐标为0,求此抛物线的解析式.【作业布置】 课本P41 第五题(3)
课题 22.1.3二次函数的图象(四) 课时 1课时 课型 新授课
学习目标 会用二次函数的性质解决问题
重点 会用二次函数的性质
难点 会用二次函数的性质
考点 会用二次函数的性质
导学流程
【旧知回顾】------不练不讲1. 抛物线开口向 ,顶点坐标是 ,对称轴是 ,当x= 时,y有最 值为 。当 时,随的增大而增大.2. 抛物线是由如何平移得到的?答: 。【自主预习】------不议不讲1.抛物线的顶点坐标为(2,-3),且经过点(3,2)求该函数的解析式?分析:如何设函数解析式?写出完整的解题过程。2.例4:要修建一个圆形喷 ( http: / / www.21cnjy.com )水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长? 解:分析:由题意可知:池中心是 ( http: / / www.21cnjy.com ) ,水管是 ,点 是喷头,线段 的长度是1米,线段 的长度是3米。 已知条件可设抛物线的解析 ( http: / / www.21cnjy.com )式为 。抛物线的解析式中有一个待定系数,所以只需再确定 个点 的坐标即可,这个点是 。求水管的长就是通过求点 的 坐标。【当堂检测】1.如图,某隧道横截面的上下轮廓线 ( http: / / www.21cnjy.com )分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米. AO= 3米,现以O点为原点,OM所在直线为x轴建立直角坐标系.(1) 直接写出点A及抛物线顶点P的坐标;(2) 求出这条抛物线的函数解析式;2.如图抛物线与轴交于A,B两点,交轴于点D,抛物线的顶点为点C求△ABD的面积。求△ABC的面积。点P是抛物线上一动点,当△ABP的面积为4时,求所有符合条件的点P的坐标。【作业布置】当堂检测第一题
课题 22.1.4二次函数的图象 课时 1课时 课型 新授课
学习目标 1.能通过配方把二次函数化成的形式,从而确定开口方向、对称轴和顶点坐标。2.熟记二次函数的顶点坐标公式;3.会画二次函数一般式的图象.
重点 利用配方法将二次函数化成的形式,求抛物线的对称轴和顶点坐标.。
难点 理解二次函数的性质
考点 利用配方法将二次函数化成的形式,求抛物线的对称轴和顶点坐标.
导学流程
【知识链接】------不做不讲1.抛物线的顶点坐标是 ;对称轴是直线 ;当= 时有最 值是 ;当 时,随的增大而增大;当 时,随的增大而减小。2. 二次函数解析式中,很容易确定抛物线的顶点坐标为 。【自主预习】------不议不讲一、自主探究(预习37页----39页)1. 尝试画二次函数的图象(练习本上试一试)2. 我们知道二次函数的图像的对称轴是直线,顶点坐标是(),利用抛物线的对称性列表,容易画出图像。对照二次函数与的解析式特点,若将二次函数变形为的形式,问题就解决了.配方可得因此,抛物线的开口向上,对称轴是直线顶点坐标是(6, 3).利用其对称性列表:x…3456789…二、总结归纳:将二次函数进行配方,得到因此,抛物线的开口方向、顶点坐标、对称轴:开口方向对称轴顶点坐标单调性【当堂检测】 1、抛物线的开口 ,对称轴是 ,顶点坐标是 ,当x 时,函数值y随x的增大而减小;当x 时,函数值y随x的增大而增大。当x= 时,函数有最 值,是y= 【作业布置】课本P41第6题(2)(4)
课题 22.2二次函数与一元二次方程(一) 课时 1课时 课型 新授课
学习目标 体会二次函数与方程之间的联系。知道二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系,
重点 一元二次方程与二次函数之间的联系与应用
难点 二次函数图像与x轴交点个数和一元二次方程的根的个数之间的关系
导学流程
【知识链接】---------不做不讲1.直线与轴交于点 ,与轴交于点 。2.一元二次方程,当Δ 时,方程有两个不相等的实数根;当Δ 时,方程有两个相等的实数根;当Δ 时,方程没有实数根;【自主预习】------不议不讲1.解下列方程(1) (2) (3)2.观察二次函数的图象,写出它们与轴的交点坐标:函数图 象交点与轴交点坐标是 与轴交点坐标是 与轴交点坐标是 3.对比第1题各方程的解,你发现什么? 【知识梳理】⑴一元二次方程的实数根就是对应的二次函数与轴交点的 .(即把代入)⑵二次函数与一元二次方程的关系如下:(一元二次方程的实数根记为)二次函数与一元二次方程 与轴有 个交点 0,方程有 的实数根与轴有 个交点;这个交点是 点 0,方程有 实数根与轴有 个交点 0,方程 实数根.⑶二次函数与轴交点坐标是 【当堂检测】1. 二次函数,当=1时,=______;当=0时,=______.2.二次函数,当=________时,=33. 已知抛物线的顶点在x轴上,则=____________.4.已知抛物线与轴有两个交点,则的取值范围是_______【作业布置】课本P47第1题 第3题
课题 22.2二次函数与一元二次方程(二) 课时 1课时 课型 新授课
学习目标 1. 能根据图象判断二次函数的符号;2.能根据图象判断一些特殊方程或不等式是否成立。
重点 能根据图象判断二次函数的符号;
考点 能根据图象判断二次函数的符号;
难点 能根据图象判断二次函数的符号;
导学流程
【知识链接】--------不做不讲根据的图象和性质填表:(的实数根记为)(1)抛物线与轴有两个交点 0;(2)抛物线与轴有一个交点 0;(3)抛物线与轴没有交点 0.【自主预习】------不议不讲1.抛物线和抛物线与轴的交点坐标分别是 和 。抛物线与轴的交点坐标分别是 .2.抛物线开口向上,所以可以判断 。对称轴是直线= ,由图象可知对称轴在轴的右侧,则>0,即 >0,已知 0,所以可以判定 0.因为抛物线与轴交于正半轴,所以 0.抛物线与轴有两个交点,所以 0;【知识梳理】⑴的符号由 决定:①开口向 0;②开口向 0.⑵的符号由 决定:① 在轴的左侧 ;② 在轴的右侧 ; ③ 是轴 0.⑶的符号由 决定:①点(0,)在轴正半轴 0;②点(0,)在原点 0; ③点(0,)在轴负半轴 0.⑷的符号由 决定:①抛物线与轴有 交点 0 方程有 实数根;②抛物线与轴有 交点 0 方程有 实数根;③抛物线与轴有 交点 0 方程 实数根; ④特别的,当抛物线与x轴只有一个交点时,这个交点就是抛物线的 点.【当堂检测】1.利用抛物线图象求解一元二次方程及二次不等式方程的根为___________;方程的根为__________;方程的根为__________不等式的解集为________;(5)不等式的解集为_____ ___;2.根据图象填空:(1)_____0;(2) 0;(3) 0;(4) 0 ;(5)______0;(6);(7);【作业布置】课本P47 第4题
课题 22.3 22.3实际问题与二次函数(一) 课时 1课时 课型 新授课
学习目标 1.通过实际问题与二次函数关系的探究,让学生掌握利用顶点坐标解决最大值(或最小值)问题的方法.2.通过对生活中实际问题的探究,体会数学建模思想.
重点 掌握利用顶点坐标解决最大值(或最小值)问题的方法.
难点 掌握利用顶点坐标解决最大值(或最小值)问题的方法.
考点 掌握利用顶点坐标解决最大值(或最小值)问题的方法.
导学流程
【导语】二次函数和实际问题,有紧密的联系,本节课就来讨论如何利用二次函数来解决实际问题.探究1.用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长L的 变化而变化。当L是多少米时,场地的面积S最大?(1)矩形的一边长为Lm,则另一边长为 矩形的面积S怎样表示 (2)本题中有几个变量 分别是 S是L的函数吗 l的取值范围是什么 (3)利用什么知识来确定L是多少时S的值最大?归纳:一般地,因为抛物线的顶点是最低(高)点,所以知道它的顶点坐标,即可知道,二次函数何时取最值.【自主预习】1.已知平行四边形ABCD的周长为8cm,∠B=30°,若边长AB=xcm.(1)写出□ABCD的面积y与x的函数关系式,并求自变量x的取值范围.(2)当x取什么值时,y的值最大 并求出最大值.【当堂检测】1.用长为8m的铝合金条制成矩形窗框,问窗框的宽和高各是多少米时,窗户的透光面积最大?最大面积是多少?某农场要盖一排三间长方形的羊圈,打算一面利用 ( http: / / www.21cnjy.com )长 为16m的旧墙,其余各面用木材围成栅栏,计划用木材围成总长为24m的栅栏,设每间羊圈与墙垂直的一边长x,三间羊围的总面积为S,则S与x的函数关系式是--------------------,x的取值范围是---------------,当x=---------时,面积S最 大,最大面积为----------------.【作业布置】 课本P51 第1、3题
课题 22.3实际问题与二次函数(二) 课时 1课时 课型 新授课
学习目标 通过实际问题与二次函数关系的探究,让学生掌握利用顶点坐标解决最大值(或最小值)问题的方法.2.通过对生活中实际问题的探究,体会数学建模思想.
重点 掌握利用顶点坐标解决最大值(或最小值)问题的方法.
难点 掌握利用顶点坐标解决最大值(或最小值)问题的方法.
考点 掌握利用顶点坐标解决最大值(或最小值)问题的方法.
导学流程
【旧知回顾】利用二次函数的性质解决许多生活和生产实际中的最大和最小值的问题,它的一般方法是:(1)列出二次函数的解析式,列解析式时,要根据自变量的实际意义,确定自变量的取值范围。(2)在自变量取值范围内,运用公式或配方法求出二次函数的最大值和最小值【自主预习】------不议不讲 探究一:某商品现在的 ( http: / / www.21cnjy.com )售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?(1)题目中有几种调整价格的方法? (2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化?分析: 调整价格包括涨价和降价两种情况设每件涨价x 元,则每星期售出的商品利润Y随之变化。我们先来确定y随x变化的函数式。涨价x元时,每星期少卖 10x 件,销售量可表示为 : 销售额可表示为: 买进商品需付: 所获利润可表示为: ∴当销售单价为 元时,可以获得最大利润, 最大利润是 元.思考:1 怎样确定x的取值范围? 2 在降价的情况下,最大利润是多少?总结归纳:解题步骤:(1)先分析问题中的数量关系,列出函数关系式;(2)研究自变量的取值范围;(3)研究所得的函数; (4)检验x的取值是否在自变量的取值范围内,并求相关的值;(5)解决提出的实际问题.【当堂检测】1.某玩具厂计划生产一种玩具熊猫,每日 ( http: / / www.21cnjy.com )最高产量为40只且每日生产的产品全部售出,已知生产x只玩具熊猫的成本为R(元) ,售价每只为P(元) ,且R、P与x的关系分 别为R = 500 + 30x , P = 170 - 2x. (1)当每日产量为多少时,每日获得利润为1750元 (2)当每日产量为多少时,可获得最大利润 最大利润是多少 【作业布置】 课本51页 第2、8题
课题 22.3实际问题与二次函数(三) 课时 1课时 课型 新授课
学习目标 1.将生活实际问题转化为数学问题,体验二次函数在生活中的应用。2. 通过对生活中实际问题的探究,体会数学在生活实际中的广泛应用,发展数学思维。
重点 利用二次函数解决有关拱桥问题
难点 利用二次函数解决有关拱桥问题
导学流程
【旧知回顾】利用二次函数的性质解决许多生活和生产实际中的最大和最小值的问题,它的一般方法是:(1)列出二次函数的解析式,列解析式时,要根据自变量的实际意义,确定自变量的取值范围。(2)在自变量取值范围内,运用公式或配方法求出二次函数的最大值和最小值。【自主预习】------不议不讲探究新知 探究3 图中是抛物线形拱桥,当拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加多少?观看石拱桥图片分析问题:1.石拱桥桥拱的形状可以近似的看成是抛物线吗?2.将本体转化为二次函数问题,需要求出 ( http: / / www.21cnjy.com )二次函数解析式,根据题中条件,求二次函数解析式的前提是什么? 3.题中“水面下降1m的含义是什么?”水面下降的同时水面宽度有什么变化?如何求宽度增加多少? ( http: / / www.21cnjy.com )思考:还有其他建立平面直角坐标系的方法吗? 二、总结归纳:1.运用二次函数解决实际问题的一般步骤:审题;建立数学模型;求抛物线解析式;解决实际问题;2.数形结合思想的运用【当堂检测】某工厂大门是一抛物线形的水泥建筑物 ( http: / / www.21cnjy.com ),大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过大门 若能,请你通过计算加以说明;若不能,请简要说明理由. ( http: / / www.21cnjy.com )【作业布置】 课本P51第4、5题
(3)
(2)
(1)
(4)
学习目标 1. 知道二次函数的有关概念.2. 会确定二次函数关系式中各项的系数。3. 确定实际问题中二次函数的关系式。
重点 知道二次函数中的有关概念,能列出实际问题中二次函数解析式
难点 能列出实际问题中二次函数解析式
导学流程
【旧知回顾】------不练不讲1.若在一个变化过程中有两个变量x和y, ( http: / / www.21cnjy.com )如果对于x的每一个值, y都有唯一的值与它对应,那么就说y是x的 ,x叫做 。2. 形如的函数是一次函数,当时,它是 函数。【自主预习】------不议不讲预习课本28页-29页内容一、探究新知1.若正方体的棱长为x,表面积为y,则y与x之间的函数关系式为 。2. n支球队参加比赛,每两队之间进行一场比赛.写出比赛的场次数m与球队数n之间的关系式_______________________.3. 某产品现有年产量20t,计划今后两 ( http: / / www.21cnjy.com )年增加产量。若每年都比上一年的产量增加x倍,两年后的产量为y,y与x之间的关系式为 。 4. 观察上述1、2、3中函数关系式有哪些共同之处? 。二、总结归纳:一般地,形如 ,( )的函数为二次函数。其中是自变量,是__________,b是___________,c是_____________.三、合作交流:(1)二次项系数为什么不等于0?答: 。(2)一次项系数和常数项可以为0吗?答: .【当堂检测】1.观察:①;②;③y=200x2+400x+200;④;⑤;⑥,这六个式子中二次函数有 。(只填序号)2. 是二次函数,则m的值为______________.3. 若物体运动的路段s(米)与时间t(秒)之间的关系为,则当t=4秒时,该物体所经过的路程为 。【作业布置】课本 第41页 第一、二题
课题 22.1.2 二次函数的图象和性质 课时 1课时 课型 新授课
学习目标 1.知道二次函数的图象是一条抛物线;2.会画二次函数y=ax2的图象;3.知道二次函数y=ax2的性质,并会灵活应用.
重点 知道二次函数y=ax2的性质,并会灵活应用
难点 知道二次函数y=ax2的性质,并会灵活应用。
考点 知道二次函数y=ax2的性质,并会灵活应用
导学流程
【旧知回顾】------不练不讲1描点法画一个函数图象的一般过程是① ;② ;③ 。2.一次函数图象的形状是 ;一次函数有那些性质呢?【自主预习】------不议不讲预习课本30页---32页练习前内容一、探究新知 (一)画二次函数y=x2的图象.列表:x…-3-2-10123…y=x2……在图(3)中描点,并连线1.思考:图(1)和图(2)中的连线正确吗?为什么?连线中我们应该注意什么?答:2.归纳:① 由图象可知二次函数的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,即抛出物体所经过的路线,所以这条曲线叫做 线;②抛物线是轴对称图形,对称轴是 ;③的图象开口_______;④ 与 的交点叫做抛物线的顶点。抛物线的顶点坐标是 ;它是抛物线的最 点(填“高”或“低”),即当x=0时,y有最 值等于0⑤在对称轴的左侧,图象从左往右呈 趋势,在对称轴的右侧,图象从左往右呈 趋势;即<0时,随的增大而 ,>0时,随的增大而 。(二)例1在图(4)中,画出函数,和,的图象。解:列表:x…-4-3-2-101234………归纳:抛物线,,的图象的形状都是 ;顶点都是__________;对称轴都是_________;二次项系数_______0;开口都 ;顶点都是抛物线的最_________点(填“高”或“低”) .抛物线,的图象的形状都是 ;顶点都是__________;对称轴都是_________;二次项系数_______0;开口都 ;顶点都是抛物线的最_________点(填“高”或“低”) .二、总结归纳1. 抛物线的性质图象(草图)对称轴顶点开口方向有最高或最低点最值>0当x=____时,y有最_______值,是______.<0当x=____时,y有最_______值,是______.2. 当>0时,在对称轴的左侧,即 0时,随的增大而 ;在对称轴的右侧,即 0时随的增大而 。3.在前面图(4)中,关于x轴对称的抛物线有 对,它们分别是哪些?答: 。由此可知和抛物线关于轴对称的抛物线是 。当>0时,越大,抛物线的开口越___________;当<0时, 越大,抛物线的开口越_________;因此,越大,抛物线的开口越________。【当堂检测】1.函数的图象顶点是__________,对称轴是________,开口向_______,当x=___________时,有最_________值是_________.2. 二次函数的图象开口向下,则m___________.3. 二次函数y=mx有最高点,则m=___________.4. 二次函数y=(k+1)x2的图象如图所示,则k的取值范围为___________.5.若二次函数的图象过点(1,-2),则的值是___________.6.如图,抛物线①② ③④ 开口从小到大排列是___________________________________;(只填序号)其中关于轴对称的两条抛物线是 和 。7.点A(,b)是抛物线上的一点,则b= ;过点A作x轴的平行线交抛物线另一点B的坐标是 。8..二次函数与直线交于点P(1,b).(1)求a、b的值;(2)写出二次函数的关系式,并指出x取何值时,该函数的y随x的增大而减小.【作业布置】 课本第41页第三、四题
课题 22.1.3二次函数的图象和性质(一) 课时 1课时 课型 新授课
学习目标 1.知道二次函数与的联系.2. 知道二次函数的性质,并会应用;
重点 知道二次函数的性质,并会应用
难点 知道二次函数的性质,并会应用
考点 知道二次函数的性质,并会应用
导学流程
【知识链接】------不练不讲1.直线可以看做是由直线 得到的。2.若一个一次函数的图象是由平移得到,并且过点(-1,3),求这个函数的解析式。由此你能推测二次函数与的图象之间又有何关系吗?猜想: 。【自主预习】------不议不讲预习32页—33页练习前内容探究新知 在同一直角坐标系中,画出二次函数,,的图象.解:列表、x…-3-2-10123…………… 描点、连线二、总结归纳:1.填表开口方向顶点对称轴有最高(低)点增减性可以发现,把抛物线向______平移______个单位,就得到抛物线; 把抛物线向_______平移______个单位,就得到抛物线.3.抛物线,,的形状_____________.开口大小相同。三、知识梳理:(一)抛物线特点:1.当时,开口向 ;当时,开口 ;2. 顶点坐标是 ;3. 对称轴是 。(二)抛物线与形状相同,位置不同,是由 平移得到的。(填上下或左右)二次函数图象的平移规律:上 下 。(三)的正负决定开口的 ;决定开口的 ,即不变,则抛物线的形 状 。因为平移没有改变抛物线的开口方向和形状,所以平移前后的两条抛物线值 。【当堂检测】1.抛物线向上平移3个单位,就得到抛物线__________________; 抛物线向下平移4个单位,就得到抛物线__________________.抛物线向上平移3个单位后的解析式为 , 它们的形状__________,当= 时,有最 值是 。由抛物线向垂直方向平移,且经过(1,7)点的抛物线的解析式是 , 是把原抛物线向 平移 个单位得到的。4. 写出一个顶点坐标为(0,-3),开口方向与抛物线的方向相反,形状相同的抛物线解析式____________________________.5. 抛物线关于x轴对称的抛物线解析式为______________________.6.二次函数的经过点A(1,-1)、B(2,5).⑴求该函数的表达式;⑵若点C(-2,),D(,7)也在函数图像上,求、的值。【作业布置】 课本P41第五题(1)
课题 22.1.3 二次函数的图象(二) 课时 2课时 课型 新授课
学习目标 1.会画二次函数的图象;2.知道二次函数与的联系.3. 知道二次函数的性质,并会应用
重点 知道二次函数的性质,并会应用
难点 知道二次函数的性质,并会应用
考点 知道二次函数的性质,并会应用
导学流程
【旧知回顾】------不练不讲1.将二次函数的图象向上平移2个单位,所得图象的解析式为 。2.将抛物线的图象向下平移3个单位后的抛物线的解析式为 。【自主预习】------不议不讲预习33页---35页练习前内容探究新知 画出二次函数,的图象;解: 先列表:…-4-3-2-101234……………描点、连线二、总结归纳:(1)的开口向 ,对称轴是直线 ,顶点坐标是 。图象有最 点,即= 时,有最 值是 ;在对称轴的左侧,即 时,随的增大而 ;在对称轴的右侧,即 时,随的增大而 。 可以看作由向 平移 个单位形成的。(2)的开口向 ,对称轴是直线 ,顶点坐标是 , 图象有最 点,即= 时,有最 值是 ;在对称轴的左侧,即 时,随的增大而 ;在对称轴的右侧,即 时随的增大而 。可以看作由向 平移 个单位形成的。可以看作由向 平移 个单位形成的。三、知识梳理(一)抛物线特点:1.当时,开口向 ;当时,开口 ;2. 顶点坐标是 ;3. 对称轴是直线 。(二)抛物线与形状相同,位置不同, 是由 平移得到的。(填上下或左右) 由学案可知二次函数图象的平移规律:左 右 ,上 下 。(三)的正负决定开口的 ;决定开口的 ,即不变,则抛物线的形状 。 因为平移没有改变抛物线的开口方向和形状,所以平移前后的两条抛物线值 。(四)抛物线与的单调性 (相同或不同)。【当堂检测】抛物线的开口_______;顶点坐标为_________; 对称轴是直线_______;当 时,随的增大而减小; 当 时,随的增大而增大。抛物线的开口_______;顶点坐标为_________; 对称轴是直线_______;当 时,随的增大而减小; 当 时,随的增大而增大。3. 抛物线的开口_______;顶点坐标为_________;对称轴是_______;4.抛物线向右平移4个单位后,得到的抛物线的表达式为______________.5. 抛物线向左平移3个单位后,得到的抛物线的表达式为______________.6.将抛物线向右平移1个单位后,得到的抛物线解析式为__________.7.抛物线与y轴的交点坐标是_______,与x轴的交点坐标为________.8. 写出一个顶点是(5,0),形状、开口方向与抛物线都相同的二次函数解析式_______________【作业布置】 课本P41第五题(2)
课题 22.1.3二次函数的图象(三) 课时 1课时 课型 新授课
学习目标 1.会画二次函数的顶点式的图象;2.知道二次函数的性质;
重点 知道二次函数的性质
难点 知道二次函数的性质
考点 知道二次函数的性质
导学流程
【旧知回顾】------不练不讲1.将二次函数的图象向上平移2个单位,所得图象的解析式为 。2.将抛物线的图象向左平移3个单位后的抛物线的解析式为 。【自主预习】------不议不讲 预习35页—36页例4前内容探究新知 在右图中做出的图象:观察:1. 抛物线开口向 ;顶点坐标是 ;对称轴是直线 。2. 抛物线和的形状 ,位置 。(填“相同”或“不同”)3. 抛物线是由如何平移得到的?答: 。二、合作交流平移前后的两条抛物线值变化吗?为什么?答: 三、总结归纳:结合上图和课本第35页例3归纳:(一)抛物线的特点:1.当时,开口向 ;当时,开口 ;2. 顶点坐标是 ;3. 对称轴是直线 。(二)抛物线与形状 ,位置不同,是由平移得到的。二次函数图象的平移规律:左 右 ,上 下 。(三)平移前后的两条抛物线值 。【当堂检测】1.二次函数的图象可由的图象( )A.向左平移1个单位,再向下平移2个单位得到 B.向左平移1个单位,再向上平移2个单位得到C.向右平移1个单位,再向下平移2个单位得到 D.向右平移1个单位,再向上平移2个单位得到2.抛物线开口 ,顶点坐标是 ,对称轴是 ,当x= 时,y有最 值为 。3.若把函数的图象分别向下、向左移动2个单位,则得到的函数解析式为 。4. 顶点坐标为(-2,3),开口方向和大小与抛物线相同的解析式为( )A. B. C. D.一条抛物线的形状、开口方向与抛物线相同,对称轴和抛物线相同,且顶点纵坐标为0,求此抛物线的解析式.【作业布置】 课本P41 第五题(3)
课题 22.1.3二次函数的图象(四) 课时 1课时 课型 新授课
学习目标 会用二次函数的性质解决问题
重点 会用二次函数的性质
难点 会用二次函数的性质
考点 会用二次函数的性质
导学流程
【旧知回顾】------不练不讲1. 抛物线开口向 ,顶点坐标是 ,对称轴是 ,当x= 时,y有最 值为 。当 时,随的增大而增大.2. 抛物线是由如何平移得到的?答: 。【自主预习】------不议不讲1.抛物线的顶点坐标为(2,-3),且经过点(3,2)求该函数的解析式?分析:如何设函数解析式?写出完整的解题过程。2.例4:要修建一个圆形喷 ( http: / / www.21cnjy.com )水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长? 解:分析:由题意可知:池中心是 ( http: / / www.21cnjy.com ) ,水管是 ,点 是喷头,线段 的长度是1米,线段 的长度是3米。 已知条件可设抛物线的解析 ( http: / / www.21cnjy.com )式为 。抛物线的解析式中有一个待定系数,所以只需再确定 个点 的坐标即可,这个点是 。求水管的长就是通过求点 的 坐标。【当堂检测】1.如图,某隧道横截面的上下轮廓线 ( http: / / www.21cnjy.com )分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米. AO= 3米,现以O点为原点,OM所在直线为x轴建立直角坐标系.(1) 直接写出点A及抛物线顶点P的坐标;(2) 求出这条抛物线的函数解析式;2.如图抛物线与轴交于A,B两点,交轴于点D,抛物线的顶点为点C求△ABD的面积。求△ABC的面积。点P是抛物线上一动点,当△ABP的面积为4时,求所有符合条件的点P的坐标。【作业布置】当堂检测第一题
课题 22.1.4二次函数的图象 课时 1课时 课型 新授课
学习目标 1.能通过配方把二次函数化成的形式,从而确定开口方向、对称轴和顶点坐标。2.熟记二次函数的顶点坐标公式;3.会画二次函数一般式的图象.
重点 利用配方法将二次函数化成的形式,求抛物线的对称轴和顶点坐标.。
难点 理解二次函数的性质
考点 利用配方法将二次函数化成的形式,求抛物线的对称轴和顶点坐标.
导学流程
【知识链接】------不做不讲1.抛物线的顶点坐标是 ;对称轴是直线 ;当= 时有最 值是 ;当 时,随的增大而增大;当 时,随的增大而减小。2. 二次函数解析式中,很容易确定抛物线的顶点坐标为 。【自主预习】------不议不讲一、自主探究(预习37页----39页)1. 尝试画二次函数的图象(练习本上试一试)2. 我们知道二次函数的图像的对称轴是直线,顶点坐标是(),利用抛物线的对称性列表,容易画出图像。对照二次函数与的解析式特点,若将二次函数变形为的形式,问题就解决了.配方可得因此,抛物线的开口向上,对称轴是直线顶点坐标是(6, 3).利用其对称性列表:x…3456789…二、总结归纳:将二次函数进行配方,得到因此,抛物线的开口方向、顶点坐标、对称轴:开口方向对称轴顶点坐标单调性【当堂检测】 1、抛物线的开口 ,对称轴是 ,顶点坐标是 ,当x 时,函数值y随x的增大而减小;当x 时,函数值y随x的增大而增大。当x= 时,函数有最 值,是y= 【作业布置】课本P41第6题(2)(4)
课题 22.2二次函数与一元二次方程(一) 课时 1课时 课型 新授课
学习目标 体会二次函数与方程之间的联系。知道二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系,
重点 一元二次方程与二次函数之间的联系与应用
难点 二次函数图像与x轴交点个数和一元二次方程的根的个数之间的关系
导学流程
【知识链接】---------不做不讲1.直线与轴交于点 ,与轴交于点 。2.一元二次方程,当Δ 时,方程有两个不相等的实数根;当Δ 时,方程有两个相等的实数根;当Δ 时,方程没有实数根;【自主预习】------不议不讲1.解下列方程(1) (2) (3)2.观察二次函数的图象,写出它们与轴的交点坐标:函数图 象交点与轴交点坐标是 与轴交点坐标是 与轴交点坐标是 3.对比第1题各方程的解,你发现什么? 【知识梳理】⑴一元二次方程的实数根就是对应的二次函数与轴交点的 .(即把代入)⑵二次函数与一元二次方程的关系如下:(一元二次方程的实数根记为)二次函数与一元二次方程 与轴有 个交点 0,方程有 的实数根与轴有 个交点;这个交点是 点 0,方程有 实数根与轴有 个交点 0,方程 实数根.⑶二次函数与轴交点坐标是 【当堂检测】1. 二次函数,当=1时,=______;当=0时,=______.2.二次函数,当=________时,=33. 已知抛物线的顶点在x轴上,则=____________.4.已知抛物线与轴有两个交点,则的取值范围是_______【作业布置】课本P47第1题 第3题
课题 22.2二次函数与一元二次方程(二) 课时 1课时 课型 新授课
学习目标 1. 能根据图象判断二次函数的符号;2.能根据图象判断一些特殊方程或不等式是否成立。
重点 能根据图象判断二次函数的符号;
考点 能根据图象判断二次函数的符号;
难点 能根据图象判断二次函数的符号;
导学流程
【知识链接】--------不做不讲根据的图象和性质填表:(的实数根记为)(1)抛物线与轴有两个交点 0;(2)抛物线与轴有一个交点 0;(3)抛物线与轴没有交点 0.【自主预习】------不议不讲1.抛物线和抛物线与轴的交点坐标分别是 和 。抛物线与轴的交点坐标分别是 .2.抛物线开口向上,所以可以判断 。对称轴是直线= ,由图象可知对称轴在轴的右侧,则>0,即 >0,已知 0,所以可以判定 0.因为抛物线与轴交于正半轴,所以 0.抛物线与轴有两个交点,所以 0;【知识梳理】⑴的符号由 决定:①开口向 0;②开口向 0.⑵的符号由 决定:① 在轴的左侧 ;② 在轴的右侧 ; ③ 是轴 0.⑶的符号由 决定:①点(0,)在轴正半轴 0;②点(0,)在原点 0; ③点(0,)在轴负半轴 0.⑷的符号由 决定:①抛物线与轴有 交点 0 方程有 实数根;②抛物线与轴有 交点 0 方程有 实数根;③抛物线与轴有 交点 0 方程 实数根; ④特别的,当抛物线与x轴只有一个交点时,这个交点就是抛物线的 点.【当堂检测】1.利用抛物线图象求解一元二次方程及二次不等式方程的根为___________;方程的根为__________;方程的根为__________不等式的解集为________;(5)不等式的解集为_____ ___;2.根据图象填空:(1)_____0;(2) 0;(3) 0;(4) 0 ;(5)______0;(6);(7);【作业布置】课本P47 第4题
课题 22.3 22.3实际问题与二次函数(一) 课时 1课时 课型 新授课
学习目标 1.通过实际问题与二次函数关系的探究,让学生掌握利用顶点坐标解决最大值(或最小值)问题的方法.2.通过对生活中实际问题的探究,体会数学建模思想.
重点 掌握利用顶点坐标解决最大值(或最小值)问题的方法.
难点 掌握利用顶点坐标解决最大值(或最小值)问题的方法.
考点 掌握利用顶点坐标解决最大值(或最小值)问题的方法.
导学流程
【导语】二次函数和实际问题,有紧密的联系,本节课就来讨论如何利用二次函数来解决实际问题.探究1.用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长L的 变化而变化。当L是多少米时,场地的面积S最大?(1)矩形的一边长为Lm,则另一边长为 矩形的面积S怎样表示 (2)本题中有几个变量 分别是 S是L的函数吗 l的取值范围是什么 (3)利用什么知识来确定L是多少时S的值最大?归纳:一般地,因为抛物线的顶点是最低(高)点,所以知道它的顶点坐标,即可知道,二次函数何时取最值.【自主预习】1.已知平行四边形ABCD的周长为8cm,∠B=30°,若边长AB=xcm.(1)写出□ABCD的面积y与x的函数关系式,并求自变量x的取值范围.(2)当x取什么值时,y的值最大 并求出最大值.【当堂检测】1.用长为8m的铝合金条制成矩形窗框,问窗框的宽和高各是多少米时,窗户的透光面积最大?最大面积是多少?某农场要盖一排三间长方形的羊圈,打算一面利用 ( http: / / www.21cnjy.com )长 为16m的旧墙,其余各面用木材围成栅栏,计划用木材围成总长为24m的栅栏,设每间羊圈与墙垂直的一边长x,三间羊围的总面积为S,则S与x的函数关系式是--------------------,x的取值范围是---------------,当x=---------时,面积S最 大,最大面积为----------------.【作业布置】 课本P51 第1、3题
课题 22.3实际问题与二次函数(二) 课时 1课时 课型 新授课
学习目标 通过实际问题与二次函数关系的探究,让学生掌握利用顶点坐标解决最大值(或最小值)问题的方法.2.通过对生活中实际问题的探究,体会数学建模思想.
重点 掌握利用顶点坐标解决最大值(或最小值)问题的方法.
难点 掌握利用顶点坐标解决最大值(或最小值)问题的方法.
考点 掌握利用顶点坐标解决最大值(或最小值)问题的方法.
导学流程
【旧知回顾】利用二次函数的性质解决许多生活和生产实际中的最大和最小值的问题,它的一般方法是:(1)列出二次函数的解析式,列解析式时,要根据自变量的实际意义,确定自变量的取值范围。(2)在自变量取值范围内,运用公式或配方法求出二次函数的最大值和最小值【自主预习】------不议不讲 探究一:某商品现在的 ( http: / / www.21cnjy.com )售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?(1)题目中有几种调整价格的方法? (2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化?分析: 调整价格包括涨价和降价两种情况设每件涨价x 元,则每星期售出的商品利润Y随之变化。我们先来确定y随x变化的函数式。涨价x元时,每星期少卖 10x 件,销售量可表示为 : 销售额可表示为: 买进商品需付: 所获利润可表示为: ∴当销售单价为 元时,可以获得最大利润, 最大利润是 元.思考:1 怎样确定x的取值范围? 2 在降价的情况下,最大利润是多少?总结归纳:解题步骤:(1)先分析问题中的数量关系,列出函数关系式;(2)研究自变量的取值范围;(3)研究所得的函数; (4)检验x的取值是否在自变量的取值范围内,并求相关的值;(5)解决提出的实际问题.【当堂检测】1.某玩具厂计划生产一种玩具熊猫,每日 ( http: / / www.21cnjy.com )最高产量为40只且每日生产的产品全部售出,已知生产x只玩具熊猫的成本为R(元) ,售价每只为P(元) ,且R、P与x的关系分 别为R = 500 + 30x , P = 170 - 2x. (1)当每日产量为多少时,每日获得利润为1750元 (2)当每日产量为多少时,可获得最大利润 最大利润是多少 【作业布置】 课本51页 第2、8题
课题 22.3实际问题与二次函数(三) 课时 1课时 课型 新授课
学习目标 1.将生活实际问题转化为数学问题,体验二次函数在生活中的应用。2. 通过对生活中实际问题的探究,体会数学在生活实际中的广泛应用,发展数学思维。
重点 利用二次函数解决有关拱桥问题
难点 利用二次函数解决有关拱桥问题
导学流程
【旧知回顾】利用二次函数的性质解决许多生活和生产实际中的最大和最小值的问题,它的一般方法是:(1)列出二次函数的解析式,列解析式时,要根据自变量的实际意义,确定自变量的取值范围。(2)在自变量取值范围内,运用公式或配方法求出二次函数的最大值和最小值。【自主预习】------不议不讲探究新知 探究3 图中是抛物线形拱桥,当拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加多少?观看石拱桥图片分析问题:1.石拱桥桥拱的形状可以近似的看成是抛物线吗?2.将本体转化为二次函数问题,需要求出 ( http: / / www.21cnjy.com )二次函数解析式,根据题中条件,求二次函数解析式的前提是什么? 3.题中“水面下降1m的含义是什么?”水面下降的同时水面宽度有什么变化?如何求宽度增加多少? ( http: / / www.21cnjy.com )思考:还有其他建立平面直角坐标系的方法吗? 二、总结归纳:1.运用二次函数解决实际问题的一般步骤:审题;建立数学模型;求抛物线解析式;解决实际问题;2.数形结合思想的运用【当堂检测】某工厂大门是一抛物线形的水泥建筑物 ( http: / / www.21cnjy.com ),大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过大门 若能,请你通过计算加以说明;若不能,请简要说明理由. ( http: / / www.21cnjy.com )【作业布置】 课本P51第4、5题
(3)
(2)
(1)
(4)
同课章节目录
