人教版数学七年级上册 2.1 第2课时多项式与整式课件(共19张PPT)
文档属性
| 名称 | 人教版数学七年级上册 2.1 第2课时多项式与整式课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 278.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 10:07:34 | ||
图片预览





文档简介
(共19张PPT)
2.1 整式
第2课时 多项式与整式
1、理解多项式及其相关概念,能判断出一个多项式是几次几项式.
2、理解整式的概念,弄清楚单项式、多项式、整式之间的区别与联系.
3、会用整式解决简单的实际问题.
教学目标
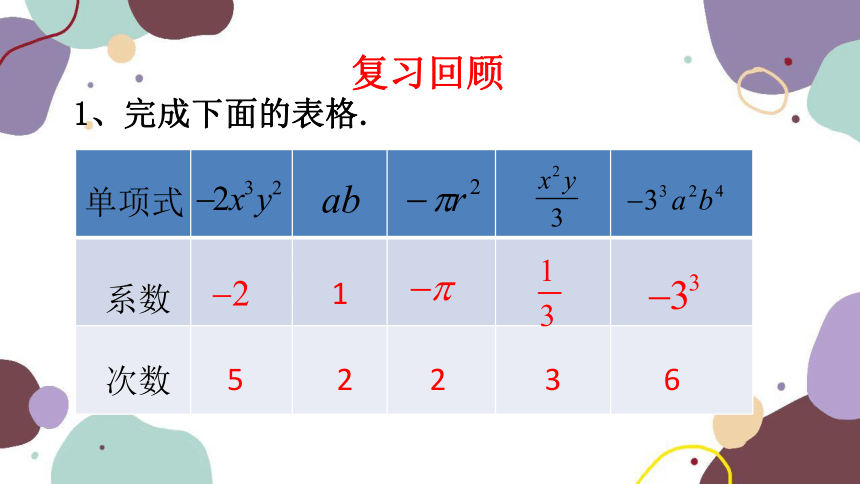
1、完成下面的表格.
1
5
2
2
3
6
单项式
系数
次数
复习回顾
要 元.
2、
买一个书包需要x元,买一支铅笔需要y 元,买一个
3、
如下图,长方形的宽为a,长为b,圆形的半径为r,
则阴影部分面积是 .
ab-πr
a
b
r
.
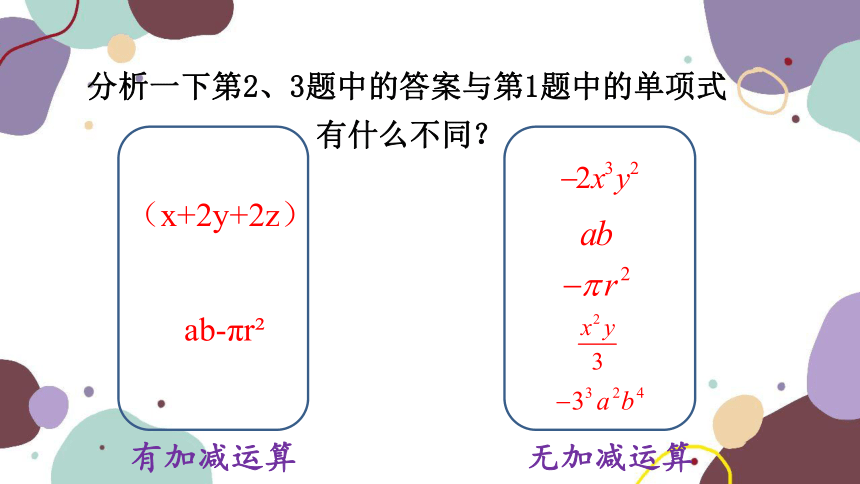
(x+2y+2z)
本子需要z元,买1个书包、2支铅笔、2个本子共需
分析一下第2、3题中的答案与第1题中的单项式
有什么不同?
(x+2y+2z)
ab-πr
有加减运算
无加减运算
以x+2y+2z为例,分析多项式的特征.
多项式定义:几个单项式的和叫做多项式.
x
2y
+
2z
+
x
2y
+
2z
+
单项式
单项式
单项式
x+2y+2z可以被分解为三个单项式,这三个单项式的和构成了x+2y+2z.
将x+2y+2z分解
单项式与多项式统称为整式.
1、判断下列各式哪些是单项式?哪些是多项式?
解:(1)和(2)是单项式.
(3)和(4)是多项式.
巩固练习
⑦
③ 1
④ xyz2
⑤ x+1
⑥ -3x
① n
⑧ 5×104x
单项式:
多项式:
.
.
整式:
.
②
⑨
⑩
①③④⑥⑦⑧⑨
⑤⑩
①③④⑤⑥⑦⑧⑨⑩
2、请根据单项式、多项式、整式的定义填空.
巩固练习
2x-3y +6
2x-3y +6是几次几项式?
分解
2x-3y +6可以被分为2x,-3y ,+6
三个单项式,所以2x-3y +6是三项式.
2x
-3y
+6
次数是1
次数是2
常数项次数可以看作0
-3y 的次数最大,是2,所以2x-3y +6
的次数是2. +6不含有未知数,所以
是常数项(次数可以看作0).
所以2x-3y +6是一个二次三项式.
指出下列多项式的项、最高次项的系数,并说出它是几次几项式;
(2)-3a2b+a2b2
(1)2xy-xy2-13
解:
(1)2xy-xy2-13的项是2xy,-xy2,-13,最高次项的系数
是-1,是三次三项式;
(2)-3a2b+a2b2的项是-3a2b,+a2b2,最高次项的系数是
+1,是四次二项式;
巩固练习
1
2
3
注意
有一个环形花坛,如图,用式子表示圆环的面积.
当R=15cm,r=10cm时,求圆环的面积(π取3.14).
解:
外圆的面积减去内圆的面积就是圆环的
面积,所以圆环的面积是πR -πr .
当R=15cm,r=10cm时,
πR -πr =3.14×15 -3.14×10
=392.5
这个圆环的面积是392.5cm .
.
r
R
例
单项式、多项式、整式的联系与区别
联系:多项式是几个单项式的和,单项式与多项式统称
整式,但不能说整式是单项式或整式是多项式.
区别:单项式的次数是所有字母的指数的和;多项式的
次数是多项式中次数最高项的次数.
(1)一个多项式是三次二项式,则这个多项式可以是( )
A.x2-2x+1 B.2x3+1 C.x2-2x D.x3-2x2+1
(2)一个多项式的次数是6次,那么它的任何一项的次数( )
1、选择题
A.都小于6 B.都等于6 C.都不小于6 D.都不大于6
B
D
随堂练习
第二排有 个座位,第n排有 个座位.如果第一排
a+1
a+n-1
有20个座位,则第19排有 个座位.
(1)在下列式子-7,-x2, ,x2+2x 中,不是整式的是 .
(2)多项式(m+1)x3y|m|+xy2+85是个四次三项式,那么m是 .
2、填空题
(3)礼堂第1排有a个座位,后面每排都比前一排多一个座位,
1
38
解:
(1)式子 四次二项式,试求a, b的值.
因为式子的次数是四次,
所以a+1=4,所以a=3.
又因为式子是二项式,
所以2b=0, 即b=0.
所以a=3, b=0.
3、计算题
(2)小王购买了一套经济适用房,他准备将地面铺上地砖,
地面结构如图所示.根据图中的数据(单位:m),用含x,y
的式子表示地面总面积.
分析:先找出该经济适用房的地面由几
部分组成,再求出它们的面积和即可.
解:
地面共由四部分组成.
由题意,得地面总面积是
6x+3×2+4×3+2y=(6x+2y+18)m
3
y
2
6
2
x
卧室
卫生间
厨房
客厅
次数:所有字母的指数的和.
系数:单项式中的数字因数.
项:算式中的每个单项式叫多项式的项.
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数.
整式
单项式
多项式
概念:由数或字母组成的式子.
概念:几个单项式的和.
小结
2.1 整式
第2课时 多项式与整式
1、理解多项式及其相关概念,能判断出一个多项式是几次几项式.
2、理解整式的概念,弄清楚单项式、多项式、整式之间的区别与联系.
3、会用整式解决简单的实际问题.
教学目标
1、完成下面的表格.
1
5
2
2
3
6
单项式
系数
次数
复习回顾
要 元.
2、
买一个书包需要x元,买一支铅笔需要y 元,买一个
3、
如下图,长方形的宽为a,长为b,圆形的半径为r,
则阴影部分面积是 .
ab-πr
a
b
r
.
(x+2y+2z)
本子需要z元,买1个书包、2支铅笔、2个本子共需
分析一下第2、3题中的答案与第1题中的单项式
有什么不同?
(x+2y+2z)
ab-πr
有加减运算
无加减运算
以x+2y+2z为例,分析多项式的特征.
多项式定义:几个单项式的和叫做多项式.
x
2y
+
2z
+
x
2y
+
2z
+
单项式
单项式
单项式
x+2y+2z可以被分解为三个单项式,这三个单项式的和构成了x+2y+2z.
将x+2y+2z分解
单项式与多项式统称为整式.
1、判断下列各式哪些是单项式?哪些是多项式?
解:(1)和(2)是单项式.
(3)和(4)是多项式.
巩固练习
⑦
③ 1
④ xyz2
⑤ x+1
⑥ -3x
① n
⑧ 5×104x
单项式:
多项式:
.
.
整式:
.
②
⑨
⑩
①③④⑥⑦⑧⑨
⑤⑩
①③④⑤⑥⑦⑧⑨⑩
2、请根据单项式、多项式、整式的定义填空.
巩固练习
2x-3y +6
2x-3y +6是几次几项式?
分解
2x-3y +6可以被分为2x,-3y ,+6
三个单项式,所以2x-3y +6是三项式.
2x
-3y
+6
次数是1
次数是2
常数项次数可以看作0
-3y 的次数最大,是2,所以2x-3y +6
的次数是2. +6不含有未知数,所以
是常数项(次数可以看作0).
所以2x-3y +6是一个二次三项式.
指出下列多项式的项、最高次项的系数,并说出它是几次几项式;
(2)-3a2b+a2b2
(1)2xy-xy2-13
解:
(1)2xy-xy2-13的项是2xy,-xy2,-13,最高次项的系数
是-1,是三次三项式;
(2)-3a2b+a2b2的项是-3a2b,+a2b2,最高次项的系数是
+1,是四次二项式;
巩固练习
1
2
3
注意
有一个环形花坛,如图,用式子表示圆环的面积.
当R=15cm,r=10cm时,求圆环的面积(π取3.14).
解:
外圆的面积减去内圆的面积就是圆环的
面积,所以圆环的面积是πR -πr .
当R=15cm,r=10cm时,
πR -πr =3.14×15 -3.14×10
=392.5
这个圆环的面积是392.5cm .
.
r
R
例
单项式、多项式、整式的联系与区别
联系:多项式是几个单项式的和,单项式与多项式统称
整式,但不能说整式是单项式或整式是多项式.
区别:单项式的次数是所有字母的指数的和;多项式的
次数是多项式中次数最高项的次数.
(1)一个多项式是三次二项式,则这个多项式可以是( )
A.x2-2x+1 B.2x3+1 C.x2-2x D.x3-2x2+1
(2)一个多项式的次数是6次,那么它的任何一项的次数( )
1、选择题
A.都小于6 B.都等于6 C.都不小于6 D.都不大于6
B
D
随堂练习
第二排有 个座位,第n排有 个座位.如果第一排
a+1
a+n-1
有20个座位,则第19排有 个座位.
(1)在下列式子-7,-x2, ,x2+2x 中,不是整式的是 .
(2)多项式(m+1)x3y|m|+xy2+85是个四次三项式,那么m是 .
2、填空题
(3)礼堂第1排有a个座位,后面每排都比前一排多一个座位,
1
38
解:
(1)式子 四次二项式,试求a, b的值.
因为式子的次数是四次,
所以a+1=4,所以a=3.
又因为式子是二项式,
所以2b=0, 即b=0.
所以a=3, b=0.
3、计算题
(2)小王购买了一套经济适用房,他准备将地面铺上地砖,
地面结构如图所示.根据图中的数据(单位:m),用含x,y
的式子表示地面总面积.
分析:先找出该经济适用房的地面由几
部分组成,再求出它们的面积和即可.
解:
地面共由四部分组成.
由题意,得地面总面积是
6x+3×2+4×3+2y=(6x+2y+18)m
3
y
2
6
2
x
卧室
卫生间
厨房
客厅
次数:所有字母的指数的和.
系数:单项式中的数字因数.
项:算式中的每个单项式叫多项式的项.
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数.
整式
单项式
多项式
概念:由数或字母组成的式子.
概念:几个单项式的和.
小结
