2014年秋高中物理必修一(新人教版):第三章第4节力的合成课件2
文档属性
| 名称 | 2014年秋高中物理必修一(新人教版):第三章第4节力的合成课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 741.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2014-09-17 08:41:19 | ||
图片预览







文档简介
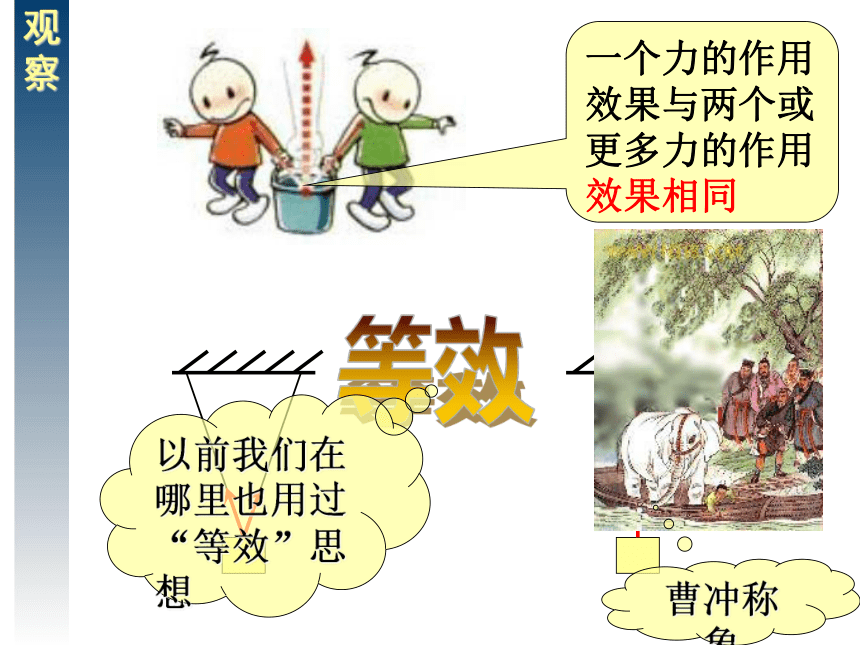
课件40张PPT。四、力的合成 关于摩擦力的易错结论:1.有摩擦力一定有弹力,但有弹力却不一定有摩擦力。2.摩擦力总是阻碍物体的相对运动或相对运动趋势。但摩擦力不一定是阻力。3.静摩擦力方向与相对运动趋势的方向相反,滑动摩擦力方向与相对运动的方向相反,它们与 运 动方向无必然联系。摩擦力可以与运动方向相同,也可以与运动方向相反,还可以与运动方向成一定夹角。
4.静止的物体可以受滑动摩擦力的作用,运动的物体可以受静摩擦力的作用。
5.静摩擦力大小一般要根据平衡条件求解。静摩擦力的大小=使物体产生相对运动趋势的外力的大小,且随外力的变化而变化。但与压力无关。最大静摩擦力的大小与正压力成正比.
滑动摩擦力大小用F=μFN去计算。FN是物体间的正压力,有时FN等于物体重力。
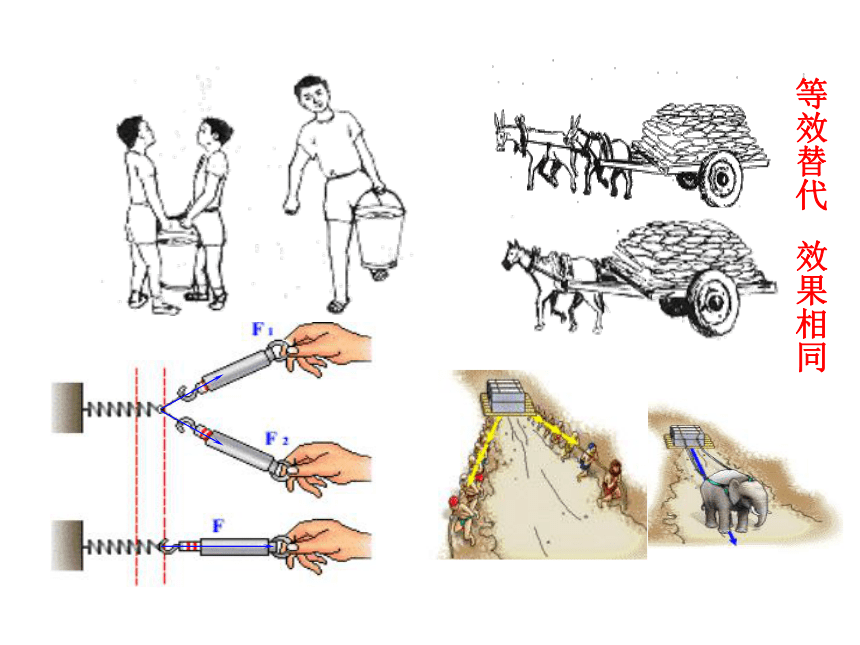
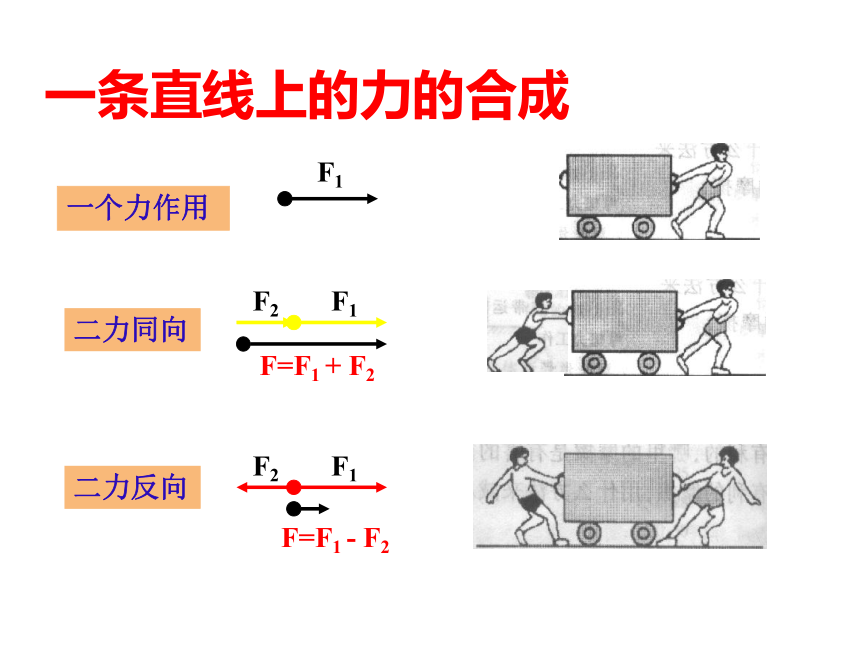
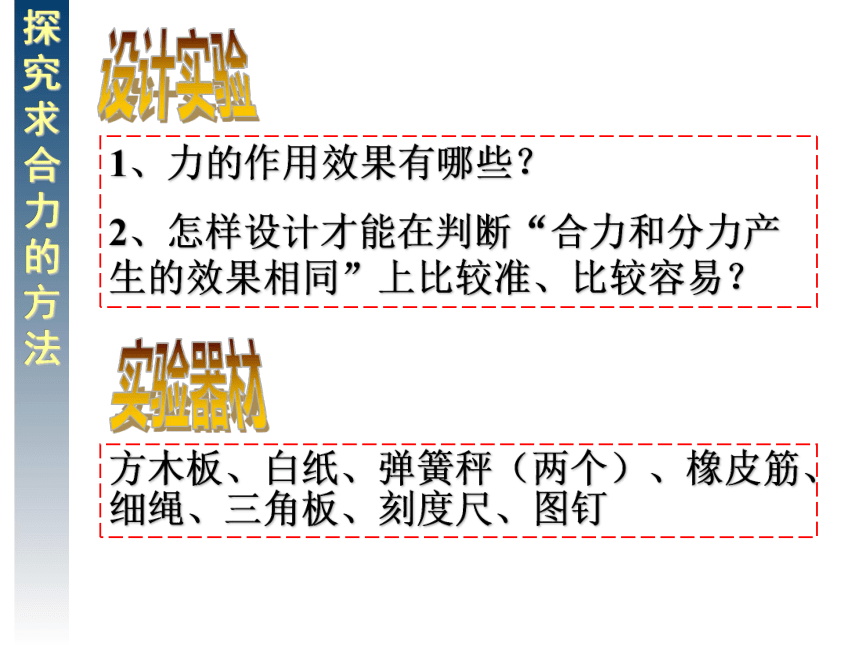
6.由于力的相互性,摩擦力的作用也是相互的(成对)1+1在什么情况下不等于2?在算错的情况下不等于2通过这节课学习我们可以知道:即使在算正确的情况下也不等于2引入新课观察一个力的作用效果与两个或更多力的作用效果相同等效以前我们在哪里也用过“等效”思想曹冲称象等效替代 效果相同1、合力: 一个力产生的效果跟几个力产生的共同效果相同,这个力叫做那几个力的合力。原来的几个力叫做分力。求几个力的合力的过程或方法,叫做力的合成说明:在实际问题中,就可以用这个力来代替那几个力,这就是力的等效代替。即合力与分力的关系是“等效替代”。而不是物体又多受了一个合力。在分析同一个问题时,合力和分力不能同时使用。也就是说,在分析问题时,考虑了合力就不能再考虑分力;考虑了分力就不能再考虑合力。 2、力的合成:力的合成就是找一个力去替代几个已知力,而不改变其作用效果一条直线上的力的合成F1F2F1F=F1 + F2F=F1 - F2一个力作用二力同向二力反向思考一个合力与两个或者更多个具有相同效果的分力,它们大小有何关系呢?探究求合力的方法?1、力的作用效果有哪些?
2、怎样设计才能在判断“合力和分力产生的效果相同”上比较准、比较容易?探究求合力的方法设计实验实验器材方木板、白纸、弹簧秤(两个)、橡皮筋、细绳、三角板、刻度尺、图钉 1、同一实验中的两只弹簧秤的选取方法是:将两只弹簧秤钩好后对拉,若两只弹簧在拉的过程中,读数相同,则可选,若不同,应另换,直至相同为止,应使拉力尽量大一些,以减小误差。
2、在满足合力不超过弹簧秤及橡皮条形变不超过弹性限度的条件下,应使拉力尽量大一些,以减小误差。
3、画力的图示时,应选定恰当的标度,尽量使图画大一些,但也不要太大而画出纸外。要严格按力的图示要求和几何作图法作出合力。
4、在同一次实验中,橡皮条拉到的结点O的位置一定要相同。
5、由作图法得到的F和测量得到的F'不可能完全符合,但在误差允许范围内可以认为F和F'符合即可。注意事项实验研究:(1)器材:
橡皮条、细绳套、钩码、滑轮
(2)步骤:
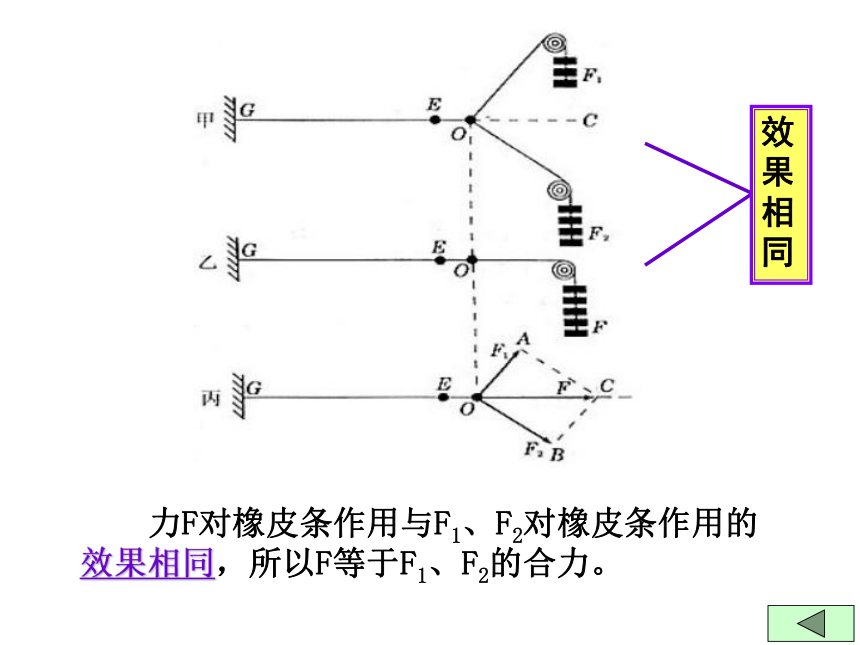
①用两个力 F1、F2将橡皮条GE沿直线EC拉长到O点,橡皮条伸长了EO这样的长度,记下O点的位置和F1、F2的大小和方向。(图甲)
②撤去F1、F2,用一个力F拉橡皮条使它沿同一直线伸长同样的长度EO,记下F的大小和方向(图乙)。
③选定标度,分别作出F1、F2、F的图示(图丙) 力F对橡皮条作用与F1、F2对橡皮条作用的效果相同,所以F等于F1、F2的合力。效果相同3、结论:3、力的合成遵循的规律:
(1)平行四边形定则:互成角度两个力的合力就是以这两个力为邻边的平行四边形的对角线。
(2)注意:
力的合成的本质就在于保证作用效果相同的前提下。
平行四边形定则是矢量运算的普遍适用的法则。
平行四边形定则只适用于共点力的情况下。F1FOF2解:(1)作图法. 则F=75N, 合力F与水平分力F1间的夹角为53°求合力的方法1 力F1=45N,方向水平向右。力F2=60N,方向竖直向上。通过作图法求这两个力的合力F的大小和方向。1、作图法:
①根据平行四边形定则按同一标度作出两个分力F1、F2力的图示;
②画出平行四边形;分力和合力要画成带箭头的实线,平行四边形的另外两条边必须画成虚线。
③量出对角线的长度,根据选定的标度求出合力的大小;
④用量角器量出合力与某个分力的夹角,表示合力的方向。求合力的方法1思考:有没其他方法呢?求合力的方法22、计算法:
根据平行四边形定则作出力的示意图,利用合力与分力组成的平行四边形内的三角形关系,求合力大小和方向。tanα=F2/F1 =4/3 如图所示,作出力的示意图,则?= 75Nα=53°4、多力合成的方法:F12F123F1234 先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力逐次合成法思考2:合力与分力的关系合力可能大于某一分力,也可能小于某一分力合力与分力的关系5、合力与分力间的关系:①θ=0°时,即F1、F2共线同方向:
F合=F1+F2 合力方向与两个力的方向相同②θ=180°时,即F1、F2共线反方向:
F合=|F1-F2|合力方向
与分力F1、F2中较大的方向相同。④合力的取值范围:|F1-F2| ≤ F合≤ F1+F2⑤当分力大小一定时,夹角θ越大,合力就越小:
F合随F1和F2的夹角增大而减小⑥当合力一定时,分力的夹角越大,两个等值分力的大小越大。F1F2F合F1F2F合③两力相互垂直时(θ=90°)合力可能大于某一分力,也可能小于、等于某一分力共点力:几个力如果都作用在物体的同一点上,或者它们的作用线相交于同一点上,这几个力叫做共点力。共点力与非共点力非共点力:力不但没有作用在同一点上,它们的延长线也不能相交于一点。力的合成的平行四边形定则,只适用于共点力。6、共点力与非共点力 例:有两个力,一个是10N,一个是2N,它们的合力能等于5N、10N、15N吗?这两个力的合力的最大值是多少?最小值是多少?强化训练:对于同一物体产生相同的效果已知分力合力力的合成平行四边形定则 以两个共点力为邻边作平行四边形,这两个邻边之间的对角线就表示合力的大小和方向求 解遵循课堂小结二、共点力
1、定义:物体受力共同作用在同一点上,或虽不作用在同 一点上,但它们的延长线交于一点。
2、二力合力的特点:
(1)当分力大小一定时,分力之间的夹角变小合力变大,夹角变大合力变小。
(2)当合力一定时,分力的夹角越大,分力越大。
(3)合力取值范围:|F2-F1|≤F合≤ |F1+F2|
(4)互成直角的两力合力:
3、多个力合成原则:先把任意两个力合成,求得合力后,在与第三个力合成,依次进行,最终求得全部共点力的合力。作业物理P64力的合成习题课1、大小确定的两个力的合力随夹角的增大而减小2、F1、F2同向共线时,合力最大,
F1、F2反向共线时,合力最小
即合力的取值范围: ︱ F1-F2︱≤F合≤F1+F23、合力可能大于某一分力,也可能小于、等于某一分力
当分力大小一定时,夹角θ越大,合力就越小:
当合力一定时,分力的夹角越大,两个等值分力的大小越大。
回顾:例:书(计算法求解)例题:落实二力合成的基本运算,体会力的矢量性。
1、书P64第1题改。
有两个共点力,一个是8N,一个是6N,它们的合力有可能等于1N、10N、15N吗?合力的最大值是多少?最小值是多少?当这两个力垂直时,它们的合力多大?
变形:(1)有三个共点力,一个是8N,一个是7N,一个是2N,这三个力的合力最大值和最小值是多少?
(2)有三个共点力,每个力的大小均为10N,合力为0,则这三个力间的夹角必满足什么关系?合力?共点的三个力合力的最大值为三个力的大小之和,最小值可能为零( 满足|F2-F3| ≤ F1≤ F2+F3 时)。 合力范围的确定
1、已知共点的分力F1、F2 : |F1-F2| ≤ F合≤ F1+F2
2、已知共点的三个分力F1、F2 、 F3
Fmax的确定:合力的最大值为三个力的大小之和Fmax= F1 +F2+F3
Fmin 的确定(设F1最大):
若三个共点力的数值能构成三角形,即满足|F2-F3| ≤ F1≤ F2+F3,则合力的最小值为0。
若三个共点力的数值不能构成三角形, Fmin=最大力-两个较小的力即Fmin= |F1-F2-F3| Δ、多个力的合成F12F123F1234先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力。若有力在一条直线上,则先将一条直线上
的力进行合成,然后再去与其他的力运用
平行四边行法则进行合成二力平衡三力平衡F合=0F合=0静止平衡静止在同平面内的三个共点力,Fmin=0时,其中两个力的合力与第三个力大小相等,方向相反矢量三角形法则: 在同平面内的三个共点力,Fmin=0时,其中两个力的合力与第三个力大小相等,方向相反,对其进行平移,三个力可组成首尾相联的矢量三角形。小结:二力平衡:F1=F2,方向相反,F合=0三力平衡:F1,F2的合力F与F3大小相等方向相反,F合=0(三力平衡与否可借助矢量三角形法则进行判断)在不能构成三角形时,需考虑三力中,其中两个力之和是否等于第三个力! {练习:1.一个物体受到了3个共点力的作用,F1=4N,F2=9N,F3=11N,它们彼此之间的夹角可以改变,则此物体所受合力最大值为________N,合力的最小值为_______N。2.物体同时受到同一平面内的三个力的作用,下列几组力的合力可能为零的是( )
A。5N,7N,8N B。5N,3N,2N C。1N,5N,10N D。1N,10N,10N3。如图所示,轻绳OA一端系在天花板上,与竖直线夹角370,轻绳OB水平,一端系在墙上,O点处挂一重为40N的物体。求:AO,BO的拉力各为多大?OBA370240ABDGN1N2FN1N2N1N2图解法常运用于分析“动态变化”
4.静止的物体可以受滑动摩擦力的作用,运动的物体可以受静摩擦力的作用。
5.静摩擦力大小一般要根据平衡条件求解。静摩擦力的大小=使物体产生相对运动趋势的外力的大小,且随外力的变化而变化。但与压力无关。最大静摩擦力的大小与正压力成正比.
滑动摩擦力大小用F=μFN去计算。FN是物体间的正压力,有时FN等于物体重力。
6.由于力的相互性,摩擦力的作用也是相互的(成对)1+1在什么情况下不等于2?在算错的情况下不等于2通过这节课学习我们可以知道:即使在算正确的情况下也不等于2引入新课观察一个力的作用效果与两个或更多力的作用效果相同等效以前我们在哪里也用过“等效”思想曹冲称象等效替代 效果相同1、合力: 一个力产生的效果跟几个力产生的共同效果相同,这个力叫做那几个力的合力。原来的几个力叫做分力。求几个力的合力的过程或方法,叫做力的合成说明:在实际问题中,就可以用这个力来代替那几个力,这就是力的等效代替。即合力与分力的关系是“等效替代”。而不是物体又多受了一个合力。在分析同一个问题时,合力和分力不能同时使用。也就是说,在分析问题时,考虑了合力就不能再考虑分力;考虑了分力就不能再考虑合力。 2、力的合成:力的合成就是找一个力去替代几个已知力,而不改变其作用效果一条直线上的力的合成F1F2F1F=F1 + F2F=F1 - F2一个力作用二力同向二力反向思考一个合力与两个或者更多个具有相同效果的分力,它们大小有何关系呢?探究求合力的方法?1、力的作用效果有哪些?
2、怎样设计才能在判断“合力和分力产生的效果相同”上比较准、比较容易?探究求合力的方法设计实验实验器材方木板、白纸、弹簧秤(两个)、橡皮筋、细绳、三角板、刻度尺、图钉 1、同一实验中的两只弹簧秤的选取方法是:将两只弹簧秤钩好后对拉,若两只弹簧在拉的过程中,读数相同,则可选,若不同,应另换,直至相同为止,应使拉力尽量大一些,以减小误差。
2、在满足合力不超过弹簧秤及橡皮条形变不超过弹性限度的条件下,应使拉力尽量大一些,以减小误差。
3、画力的图示时,应选定恰当的标度,尽量使图画大一些,但也不要太大而画出纸外。要严格按力的图示要求和几何作图法作出合力。
4、在同一次实验中,橡皮条拉到的结点O的位置一定要相同。
5、由作图法得到的F和测量得到的F'不可能完全符合,但在误差允许范围内可以认为F和F'符合即可。注意事项实验研究:(1)器材:
橡皮条、细绳套、钩码、滑轮
(2)步骤:
①用两个力 F1、F2将橡皮条GE沿直线EC拉长到O点,橡皮条伸长了EO这样的长度,记下O点的位置和F1、F2的大小和方向。(图甲)
②撤去F1、F2,用一个力F拉橡皮条使它沿同一直线伸长同样的长度EO,记下F的大小和方向(图乙)。
③选定标度,分别作出F1、F2、F的图示(图丙) 力F对橡皮条作用与F1、F2对橡皮条作用的效果相同,所以F等于F1、F2的合力。效果相同3、结论:3、力的合成遵循的规律:
(1)平行四边形定则:互成角度两个力的合力就是以这两个力为邻边的平行四边形的对角线。
(2)注意:
力的合成的本质就在于保证作用效果相同的前提下。
平行四边形定则是矢量运算的普遍适用的法则。
平行四边形定则只适用于共点力的情况下。F1FOF2解:(1)作图法. 则F=75N, 合力F与水平分力F1间的夹角为53°求合力的方法1 力F1=45N,方向水平向右。力F2=60N,方向竖直向上。通过作图法求这两个力的合力F的大小和方向。1、作图法:
①根据平行四边形定则按同一标度作出两个分力F1、F2力的图示;
②画出平行四边形;分力和合力要画成带箭头的实线,平行四边形的另外两条边必须画成虚线。
③量出对角线的长度,根据选定的标度求出合力的大小;
④用量角器量出合力与某个分力的夹角,表示合力的方向。求合力的方法1思考:有没其他方法呢?求合力的方法22、计算法:
根据平行四边形定则作出力的示意图,利用合力与分力组成的平行四边形内的三角形关系,求合力大小和方向。tanα=F2/F1 =4/3 如图所示,作出力的示意图,则?= 75Nα=53°4、多力合成的方法:F12F123F1234 先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力逐次合成法思考2:合力与分力的关系合力可能大于某一分力,也可能小于某一分力合力与分力的关系5、合力与分力间的关系:①θ=0°时,即F1、F2共线同方向:
F合=F1+F2 合力方向与两个力的方向相同②θ=180°时,即F1、F2共线反方向:
F合=|F1-F2|合力方向
与分力F1、F2中较大的方向相同。④合力的取值范围:|F1-F2| ≤ F合≤ F1+F2⑤当分力大小一定时,夹角θ越大,合力就越小:
F合随F1和F2的夹角增大而减小⑥当合力一定时,分力的夹角越大,两个等值分力的大小越大。F1F2F合F1F2F合③两力相互垂直时(θ=90°)合力可能大于某一分力,也可能小于、等于某一分力共点力:几个力如果都作用在物体的同一点上,或者它们的作用线相交于同一点上,这几个力叫做共点力。共点力与非共点力非共点力:力不但没有作用在同一点上,它们的延长线也不能相交于一点。力的合成的平行四边形定则,只适用于共点力。6、共点力与非共点力 例:有两个力,一个是10N,一个是2N,它们的合力能等于5N、10N、15N吗?这两个力的合力的最大值是多少?最小值是多少?强化训练:对于同一物体产生相同的效果已知分力合力力的合成平行四边形定则 以两个共点力为邻边作平行四边形,这两个邻边之间的对角线就表示合力的大小和方向求 解遵循课堂小结二、共点力
1、定义:物体受力共同作用在同一点上,或虽不作用在同 一点上,但它们的延长线交于一点。
2、二力合力的特点:
(1)当分力大小一定时,分力之间的夹角变小合力变大,夹角变大合力变小。
(2)当合力一定时,分力的夹角越大,分力越大。
(3)合力取值范围:|F2-F1|≤F合≤ |F1+F2|
(4)互成直角的两力合力:
3、多个力合成原则:先把任意两个力合成,求得合力后,在与第三个力合成,依次进行,最终求得全部共点力的合力。作业物理P64力的合成习题课1、大小确定的两个力的合力随夹角的增大而减小2、F1、F2同向共线时,合力最大,
F1、F2反向共线时,合力最小
即合力的取值范围: ︱ F1-F2︱≤F合≤F1+F23、合力可能大于某一分力,也可能小于、等于某一分力
当分力大小一定时,夹角θ越大,合力就越小:
当合力一定时,分力的夹角越大,两个等值分力的大小越大。
回顾:例:书(计算法求解)例题:落实二力合成的基本运算,体会力的矢量性。
1、书P64第1题改。
有两个共点力,一个是8N,一个是6N,它们的合力有可能等于1N、10N、15N吗?合力的最大值是多少?最小值是多少?当这两个力垂直时,它们的合力多大?
变形:(1)有三个共点力,一个是8N,一个是7N,一个是2N,这三个力的合力最大值和最小值是多少?
(2)有三个共点力,每个力的大小均为10N,合力为0,则这三个力间的夹角必满足什么关系?合力?共点的三个力合力的最大值为三个力的大小之和,最小值可能为零( 满足|F2-F3| ≤ F1≤ F2+F3 时)。 合力范围的确定
1、已知共点的分力F1、F2 : |F1-F2| ≤ F合≤ F1+F2
2、已知共点的三个分力F1、F2 、 F3
Fmax的确定:合力的最大值为三个力的大小之和Fmax= F1 +F2+F3
Fmin 的确定(设F1最大):
若三个共点力的数值能构成三角形,即满足|F2-F3| ≤ F1≤ F2+F3,则合力的最小值为0。
若三个共点力的数值不能构成三角形, Fmin=最大力-两个较小的力即Fmin= |F1-F2-F3| Δ、多个力的合成F12F123F1234先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力。若有力在一条直线上,则先将一条直线上
的力进行合成,然后再去与其他的力运用
平行四边行法则进行合成二力平衡三力平衡F合=0F合=0静止平衡静止在同平面内的三个共点力,Fmin=0时,其中两个力的合力与第三个力大小相等,方向相反矢量三角形法则: 在同平面内的三个共点力,Fmin=0时,其中两个力的合力与第三个力大小相等,方向相反,对其进行平移,三个力可组成首尾相联的矢量三角形。小结:二力平衡:F1=F2,方向相反,F合=0三力平衡:F1,F2的合力F与F3大小相等方向相反,F合=0(三力平衡与否可借助矢量三角形法则进行判断)在不能构成三角形时,需考虑三力中,其中两个力之和是否等于第三个力! {练习:1.一个物体受到了3个共点力的作用,F1=4N,F2=9N,F3=11N,它们彼此之间的夹角可以改变,则此物体所受合力最大值为________N,合力的最小值为_______N。2.物体同时受到同一平面内的三个力的作用,下列几组力的合力可能为零的是( )
A。5N,7N,8N B。5N,3N,2N C。1N,5N,10N D。1N,10N,10N3。如图所示,轻绳OA一端系在天花板上,与竖直线夹角370,轻绳OB水平,一端系在墙上,O点处挂一重为40N的物体。求:AO,BO的拉力各为多大?OBA370240ABDGN1N2FN1N2N1N2图解法常运用于分析“动态变化”
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
