2014年秋高中物理必修一(新人教版):第三章第5节力的分解课件1
文档属性
| 名称 | 2014年秋高中物理必修一(新人教版):第三章第5节力的分解课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2014-09-17 14:32:53 | ||
图片预览







文档简介
课件21张PPT。力的分解学习目标:
1.知道分力的概念及力的分解的含义。认识到力的分解与力的合成互为逆运算并满足平行四边形定则。
2.了解力的分解具有惟一性的条件。掌握根据力的效果进行分解的方法。第5节重点
1.理解力的分解是力的合成的逆运算,利用平行四边形进行力的分解。
2.如何判定力的作用效果及分力的确定。
难点
1.力的分解具有惟一性的条件。
2.正确确定分力的方向。
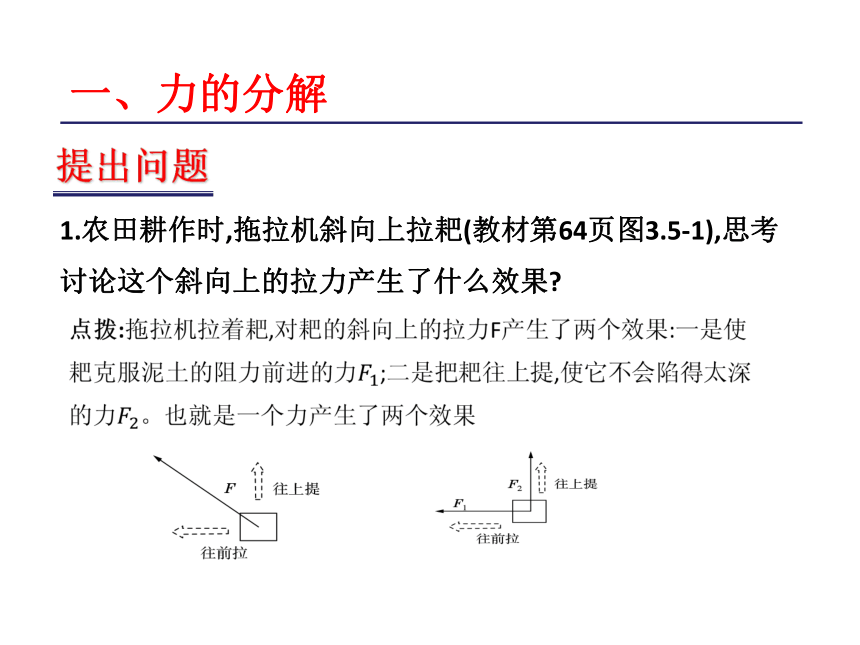
3.求解分力大小的数学方法。重点难点一、力的分解提出问题1.农田耕作时,拖拉机斜向上拉耙(教材第64页图3.5-1),思考讨论这个斜向上的拉力产生了什么效果??一、力的分解提出问题??一、力的分解提出问题3.力的合成遵守平行四边形定则,力的分解遵守什么规律?
点拨:力的分解是力的合成的逆运算,遵守平行四边形定则。
4.画出一条直线,以这条直线为对角线尝试作出平行四边形。根据作出的结果说明以这条对角线能作出多少平行四边形?
点拨:同一条对角线可以作出无数个不同的平行四边形。一、力的分解5.对同一条对角线可以作出无数个不同的平行四边形,观察演示实验,总结如何对力进行分解?
[器材]台秤、木块(一侧面带羊眼)、带有滑轮的支架各一个,钩码、细线若干.
[步骤]
①把木块放在台秤上,如图3-5-18,在实验记录表中第一行记录台秤的读数。
②用细绳一端与木块上的羊眼相连,另一端与钩码相连,并把绳子挂在支架上的滑轮上。保持滑轮的高度不变,增加绳上的钩码,在表中记录台秤相应的读数。
③保持钩码不变,改变滑轮的高度h,在表格中记录台秤相应的读数。
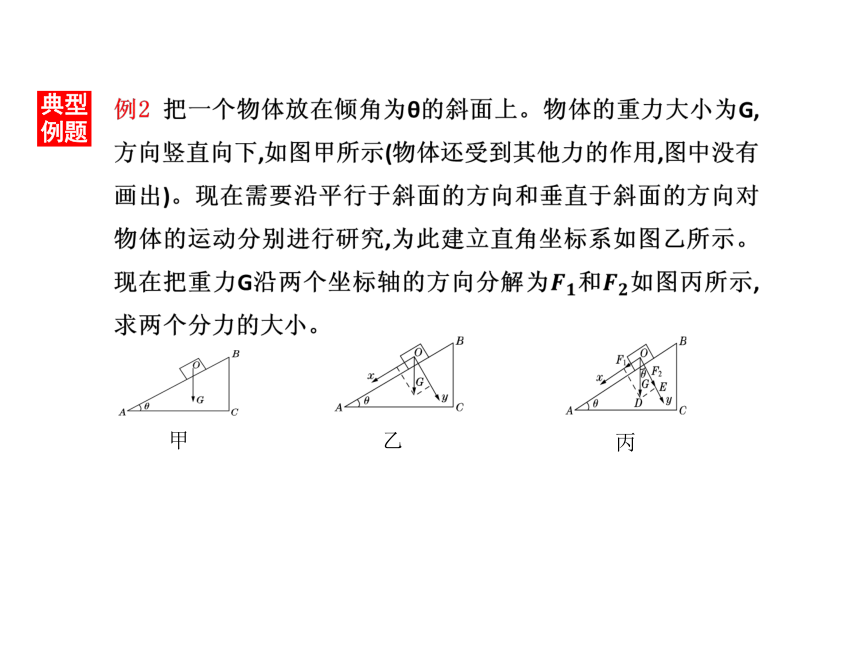
典型例题例1 放在水平面上的物体受一个斜向上方、与水平面成θ角的拉力F,这个力的作用效果如何?大小多大?解析:当θ=0°时,F水平,只有向前拉的效果;当θ=90°时,F竖直,只有向上提的效果。当力F与水平面成θ角时,力F产生向前拉的效果和向上提的效果,因此可以将力F沿水平方向和竖直方向分解。?典型例题?甲乙丙?典型例题例3 如图所示,一光滑小球放在倾角为 的光滑斜面和竖直的挡板之间,则小球对斜面的压力F1与挡板的压力F2分别多大??典型例题例4 如图所示的三角架,AB段水平,BC段与竖直方向成53°角,B端挂有一个重3N的物体,B点受到一个F=3N方向向下的作用力,试将此力分解,求其两个分力的大小及方向。解析:根据力的作用效果可知,力F可以分解成沿AB方向的拉力F1和沿BC方向的压力F2。
作平行四边形,如图所示。由几何关系,可知
F1= =4N(方向A指向B)
F2= =5N(方向由B指向C)。
答案:4N(方向A指向B) 5N(方向由B指向C)
总结:求一个已知力的实际分力的方法步骤:
(1)根据物体所处的状态分析力的作用效果;
(2)根据力的作用效果,确定两个实际分力的方向;
(3)根据两个分力的方向画出平行四边形;
(4)由平行四边形利用几何知识求两个分力。一、力的分解二、矢量相加的定则提出问题?二、矢量相加的定则提出问题?典型例题例5 已知F1和F2作用于同一点,如图所示。试求它们的合力?二、矢量相加的定则提出问题4.我们在第一章第2节学习了有关矢量和标量的概念,通过今天的学习说明矢量和标量在运算过程中运算法则有什么不同?
点拨:矢量相加时,遵守平行四边形定则或三角形定则。
标量相加时,遵守算术法则。
5.矢量相加时,要按照平行四边形定则或三角形定则,若性质相同的矢量,在同一条直线上,如何求和?
点拨:在同一条直线上的矢量相加时,在规定好了正方向的条件下,可以把矢量运算转化为代数运算。将各量直接相加,但各量“+”“-”要同时带入。巩固练习1. (多选)关于力的分解,下列说法正确的是( )
A.力的分解的本质就是用同时作用于物体的几个力产生的效果代替一个力的作用效果
B.分力的大小一定大于合力的大小
C.力的分解是力的合成的逆运算,同样遵循平行四边形定则
D.分解一个力往往根据它产生的效果来分解ACD巩固练习2.(单选)图所示用一根细绳和一根轻直杆组成三角支架,绳的一端绕在手指上,杆的一端顶在掌心,当A处挂上重物时,绳与杆对手指和手掌均有作用,对这两个作用力的方向判断完全正确的是图中的( D )ABCD巩固练习3.(多选)以下说法中正确的是( CD )
A.2 N的力可以分解成6 N和3 N的两个分力
B.10 N的力可以分解成5 N和4 N的两个分力
C.2 N的力可以分解成6 N和5 N的两个分力
D.10 N的力可以分解成两个10 N的分力巩固练习4.请将图中电线OC对O点的拉力F按其作用效果进行分解。解析:如图所示,电线OC对O点的拉力等于灯的重力,电线AO、BO都被拉紧,可见,OC上向下的拉力可分解为斜向下拉紧AO的力F1和水平向左拉紧BO的力F2.布置作业
完成[课时学案]中交流讨论的内容
1.知道分力的概念及力的分解的含义。认识到力的分解与力的合成互为逆运算并满足平行四边形定则。
2.了解力的分解具有惟一性的条件。掌握根据力的效果进行分解的方法。第5节重点
1.理解力的分解是力的合成的逆运算,利用平行四边形进行力的分解。
2.如何判定力的作用效果及分力的确定。
难点
1.力的分解具有惟一性的条件。
2.正确确定分力的方向。
3.求解分力大小的数学方法。重点难点一、力的分解提出问题1.农田耕作时,拖拉机斜向上拉耙(教材第64页图3.5-1),思考讨论这个斜向上的拉力产生了什么效果??一、力的分解提出问题??一、力的分解提出问题3.力的合成遵守平行四边形定则,力的分解遵守什么规律?
点拨:力的分解是力的合成的逆运算,遵守平行四边形定则。
4.画出一条直线,以这条直线为对角线尝试作出平行四边形。根据作出的结果说明以这条对角线能作出多少平行四边形?
点拨:同一条对角线可以作出无数个不同的平行四边形。一、力的分解5.对同一条对角线可以作出无数个不同的平行四边形,观察演示实验,总结如何对力进行分解?
[器材]台秤、木块(一侧面带羊眼)、带有滑轮的支架各一个,钩码、细线若干.
[步骤]
①把木块放在台秤上,如图3-5-18,在实验记录表中第一行记录台秤的读数。
②用细绳一端与木块上的羊眼相连,另一端与钩码相连,并把绳子挂在支架上的滑轮上。保持滑轮的高度不变,增加绳上的钩码,在表中记录台秤相应的读数。
③保持钩码不变,改变滑轮的高度h,在表格中记录台秤相应的读数。
典型例题例1 放在水平面上的物体受一个斜向上方、与水平面成θ角的拉力F,这个力的作用效果如何?大小多大?解析:当θ=0°时,F水平,只有向前拉的效果;当θ=90°时,F竖直,只有向上提的效果。当力F与水平面成θ角时,力F产生向前拉的效果和向上提的效果,因此可以将力F沿水平方向和竖直方向分解。?典型例题?甲乙丙?典型例题例3 如图所示,一光滑小球放在倾角为 的光滑斜面和竖直的挡板之间,则小球对斜面的压力F1与挡板的压力F2分别多大??典型例题例4 如图所示的三角架,AB段水平,BC段与竖直方向成53°角,B端挂有一个重3N的物体,B点受到一个F=3N方向向下的作用力,试将此力分解,求其两个分力的大小及方向。解析:根据力的作用效果可知,力F可以分解成沿AB方向的拉力F1和沿BC方向的压力F2。
作平行四边形,如图所示。由几何关系,可知
F1= =4N(方向A指向B)
F2= =5N(方向由B指向C)。
答案:4N(方向A指向B) 5N(方向由B指向C)
总结:求一个已知力的实际分力的方法步骤:
(1)根据物体所处的状态分析力的作用效果;
(2)根据力的作用效果,确定两个实际分力的方向;
(3)根据两个分力的方向画出平行四边形;
(4)由平行四边形利用几何知识求两个分力。一、力的分解二、矢量相加的定则提出问题?二、矢量相加的定则提出问题?典型例题例5 已知F1和F2作用于同一点,如图所示。试求它们的合力?二、矢量相加的定则提出问题4.我们在第一章第2节学习了有关矢量和标量的概念,通过今天的学习说明矢量和标量在运算过程中运算法则有什么不同?
点拨:矢量相加时,遵守平行四边形定则或三角形定则。
标量相加时,遵守算术法则。
5.矢量相加时,要按照平行四边形定则或三角形定则,若性质相同的矢量,在同一条直线上,如何求和?
点拨:在同一条直线上的矢量相加时,在规定好了正方向的条件下,可以把矢量运算转化为代数运算。将各量直接相加,但各量“+”“-”要同时带入。巩固练习1. (多选)关于力的分解,下列说法正确的是( )
A.力的分解的本质就是用同时作用于物体的几个力产生的效果代替一个力的作用效果
B.分力的大小一定大于合力的大小
C.力的分解是力的合成的逆运算,同样遵循平行四边形定则
D.分解一个力往往根据它产生的效果来分解ACD巩固练习2.(单选)图所示用一根细绳和一根轻直杆组成三角支架,绳的一端绕在手指上,杆的一端顶在掌心,当A处挂上重物时,绳与杆对手指和手掌均有作用,对这两个作用力的方向判断完全正确的是图中的( D )ABCD巩固练习3.(多选)以下说法中正确的是( CD )
A.2 N的力可以分解成6 N和3 N的两个分力
B.10 N的力可以分解成5 N和4 N的两个分力
C.2 N的力可以分解成6 N和5 N的两个分力
D.10 N的力可以分解成两个10 N的分力巩固练习4.请将图中电线OC对O点的拉力F按其作用效果进行分解。解析:如图所示,电线OC对O点的拉力等于灯的重力,电线AO、BO都被拉紧,可见,OC上向下的拉力可分解为斜向下拉紧AO的力F1和水平向左拉紧BO的力F2.布置作业
完成[课时学案]中交流讨论的内容
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
