人教版数学七年级上册第3章3.1.1 一元一次方程课件(27张PPT)
文档属性
| 名称 | 人教版数学七年级上册第3章3.1.1 一元一次方程课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 10:24:03 | ||
图片预览








文档简介
(共27张PPT)
第28课时 一元一次方程
第一部分 新课内容
第三章 一元一次方程
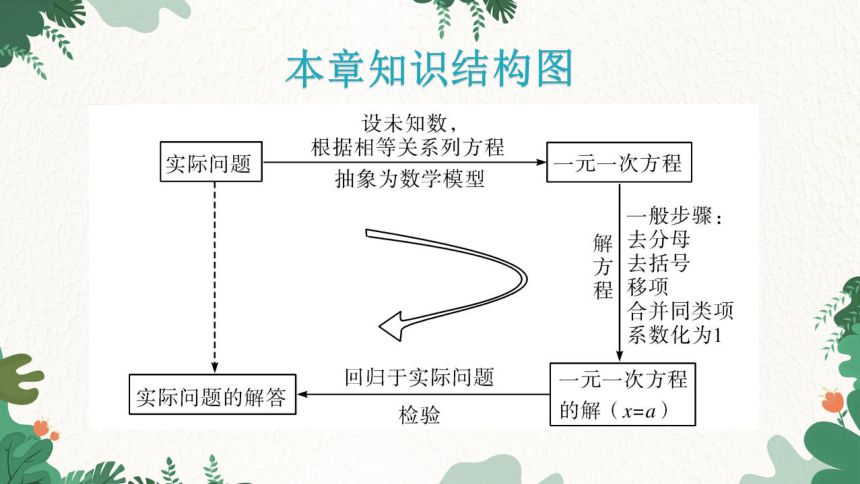
本章知识结构图
核心内容
一元一次方程及方程的解 只含有一个未知数(元),未知数的次数都是1,等号两边都是整式,这样的方程叫做一元一次方程
解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解
等式的性质 等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.即如果a=b,那么a±c=b±c.
续表
一元一次方程的解法 解一元一次方程的一般步骤包括:去分母、去括号、移项、合并同类项、系数化为1等.这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各步骤都是为了使以x为未知数的方程逐渐向x=a的形式转化
对于有分母的一元二次方程,要根据等式的性质2,左右两边同时乘各分母的最小公倍数,去分母
如果方程有括号,一般要按照去括号法则先去括号
1.把等式一边的某项变号后移到另一边,叫做移项.
2.移项的目的是将含有未知数的项移到等号左边,常数项移到等号右边,经合并同类项化为ax=b(a,b为常数)的形式.移项不同于加法交换律中的交换位置,移项一定是从等号的一边移到另一边,且一定要变号
续表
一元一次方程的解法
在解一元一次方程的过程中,合并同类项就是指合并含有未知数的项和合并常数项,从而把方程转化为ax=b,使其更接近x=a的形式(其中a,b是常数).合并同类项起到了“化简”的作用,为系数化为1作基础
续表
一元一次方程的应用 列一元一次方程解应用题的五个步骤:①审:仔细审题,确定已知量和未知量,找出它们之间的等量关系;②设:设未知数x,根据实际情况,可设直接未知数(问什么设什么),也可设间接未知数;③列:根据等量关系列出方程;④解:解方程,求出未知数的值;⑤答:检验未知数的值是否正确,是否符合题意,完整地写出答句
目录
01
知识点导学
02
典型例题
03
变式训练
04
分层训练
知识点导学
未知数
一
一
整式
①②④
相等
②③
知识点1:一元一次方程的定义
典型例题
A
变式训练
A
知识点2:根据一元一次方程的定义求字母的值
【例2】 已知xm-1-6=0是关于x的一元一次方程,则m的值
是( )
A.1 B.-1 C.-2 D.2
典型例题
D
变式训练
B
知识点3:方程的解
典型例题
D
变式训练
3. 检验括号里的数是否为方程的解:
3x-8=x-6(x=-1,x=1).
解:当x=-1时,左边=-3-8=-11,右边=-1-6=-7,左边≠右边,
所以x=-1不是原方程的解;
当x=1时,左边=3×1-8=-5,右边=1-6=-5,左边=右边,
所以x=1是原方程的解.
综上所述,x=1是原方程的解.
知识点4:根据条件,列出一元一次方程
典型例题
【例4】 根据条件,设出未知数,列方程:
(1)某数的4倍比4小5:_____________________________;
(2)小明买1个文具盒和6支彩色笔,一共花去15.5元,已知每个文具盒6.5元,求每支彩色笔多少元:
__________________________________________________.
设这个数为x,列方程为4x+5=4
设每支彩色笔x元,列方程为6.5×1+6x=15.5
变式训练
4. 根据条件,设出未知数,列方程:
(1)某数比它的2倍小3:__________________________________;
(2)用一根长24 m的铁丝围成一个正方形,求正方形的边长是多少米:
_____________________________________________________.
设这个数为x,列方程为2x-x=3
设正方形的边长为x m,列方程为4x=24
分层训练
B
C
C
D
3
B组
11.如果方程(m-1)x+2=0是关于x的一元一次方程,那么m的取值范围是( )
A. m≠0 B. m≠1
C. m=-1 D. m=0
B
12.如果关于x的方程(a-3)x|a-2|+6=0是一元一次方程,那么a的值为( )
A.3 B.2
C.3或1 D.1
13. 写出一个解为x=3的一元一次方程:____________________.
14.已知x=3是关于x的一元一次方程mx+n=1的解,则6m+2n的值为______________.
D
x-3=0(答案不唯一)
2
x-2x=1
2[x+(x+2)]=20
0.52x-(1-0.52)x=80
C组
16. 在一次植树活动中,甲、乙两班共植树55棵,其中乙班植树的棵数比甲班的一半多10棵.
(1)根据题意,设出未知数,列方程;
(2)检验甲班植树的棵数是否为25棵?是否为30棵?
17. 设未知数,列方程不解答:
(1)五一节期间,某电器按成本价提高30%后标价,再打八折(标价的80%)销售,售价为2 080元,求该电器的成本价;
(2)甲、乙两人分别用20元和10元买了一本同样的书,结果营业员找给甲的零钱是找给乙的零钱的6倍,求这本书的价格.
解:(1)设该电器的成本价为x元.
列方程,得(x+30%x)×80%=2 080.
(2)设这本书的价格是x元.
列方程,得20-x=6(10-x).
谢 谢
第28课时 一元一次方程
第一部分 新课内容
第三章 一元一次方程
本章知识结构图
核心内容
一元一次方程及方程的解 只含有一个未知数(元),未知数的次数都是1,等号两边都是整式,这样的方程叫做一元一次方程
解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解
等式的性质 等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.即如果a=b,那么a±c=b±c.
续表
一元一次方程的解法 解一元一次方程的一般步骤包括:去分母、去括号、移项、合并同类项、系数化为1等.这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各步骤都是为了使以x为未知数的方程逐渐向x=a的形式转化
对于有分母的一元二次方程,要根据等式的性质2,左右两边同时乘各分母的最小公倍数,去分母
如果方程有括号,一般要按照去括号法则先去括号
1.把等式一边的某项变号后移到另一边,叫做移项.
2.移项的目的是将含有未知数的项移到等号左边,常数项移到等号右边,经合并同类项化为ax=b(a,b为常数)的形式.移项不同于加法交换律中的交换位置,移项一定是从等号的一边移到另一边,且一定要变号
续表
一元一次方程的解法
在解一元一次方程的过程中,合并同类项就是指合并含有未知数的项和合并常数项,从而把方程转化为ax=b,使其更接近x=a的形式(其中a,b是常数).合并同类项起到了“化简”的作用,为系数化为1作基础
续表
一元一次方程的应用 列一元一次方程解应用题的五个步骤:①审:仔细审题,确定已知量和未知量,找出它们之间的等量关系;②设:设未知数x,根据实际情况,可设直接未知数(问什么设什么),也可设间接未知数;③列:根据等量关系列出方程;④解:解方程,求出未知数的值;⑤答:检验未知数的值是否正确,是否符合题意,完整地写出答句
目录
01
知识点导学
02
典型例题
03
变式训练
04
分层训练
知识点导学
未知数
一
一
整式
①②④
相等
②③
知识点1:一元一次方程的定义
典型例题
A
变式训练
A
知识点2:根据一元一次方程的定义求字母的值
【例2】 已知xm-1-6=0是关于x的一元一次方程,则m的值
是( )
A.1 B.-1 C.-2 D.2
典型例题
D
变式训练
B
知识点3:方程的解
典型例题
D
变式训练
3. 检验括号里的数是否为方程的解:
3x-8=x-6(x=-1,x=1).
解:当x=-1时,左边=-3-8=-11,右边=-1-6=-7,左边≠右边,
所以x=-1不是原方程的解;
当x=1时,左边=3×1-8=-5,右边=1-6=-5,左边=右边,
所以x=1是原方程的解.
综上所述,x=1是原方程的解.
知识点4:根据条件,列出一元一次方程
典型例题
【例4】 根据条件,设出未知数,列方程:
(1)某数的4倍比4小5:_____________________________;
(2)小明买1个文具盒和6支彩色笔,一共花去15.5元,已知每个文具盒6.5元,求每支彩色笔多少元:
__________________________________________________.
设这个数为x,列方程为4x+5=4
设每支彩色笔x元,列方程为6.5×1+6x=15.5
变式训练
4. 根据条件,设出未知数,列方程:
(1)某数比它的2倍小3:__________________________________;
(2)用一根长24 m的铁丝围成一个正方形,求正方形的边长是多少米:
_____________________________________________________.
设这个数为x,列方程为2x-x=3
设正方形的边长为x m,列方程为4x=24
分层训练
B
C
C
D
3
B组
11.如果方程(m-1)x+2=0是关于x的一元一次方程,那么m的取值范围是( )
A. m≠0 B. m≠1
C. m=-1 D. m=0
B
12.如果关于x的方程(a-3)x|a-2|+6=0是一元一次方程,那么a的值为( )
A.3 B.2
C.3或1 D.1
13. 写出一个解为x=3的一元一次方程:____________________.
14.已知x=3是关于x的一元一次方程mx+n=1的解,则6m+2n的值为______________.
D
x-3=0(答案不唯一)
2
x-2x=1
2[x+(x+2)]=20
0.52x-(1-0.52)x=80
C组
16. 在一次植树活动中,甲、乙两班共植树55棵,其中乙班植树的棵数比甲班的一半多10棵.
(1)根据题意,设出未知数,列方程;
(2)检验甲班植树的棵数是否为25棵?是否为30棵?
17. 设未知数,列方程不解答:
(1)五一节期间,某电器按成本价提高30%后标价,再打八折(标价的80%)销售,售价为2 080元,求该电器的成本价;
(2)甲、乙两人分别用20元和10元买了一本同样的书,结果营业员找给甲的零钱是找给乙的零钱的6倍,求这本书的价格.
解:(1)设该电器的成本价为x元.
列方程,得(x+30%x)×80%=2 080.
(2)设这本书的价格是x元.
列方程,得20-x=6(10-x).
谢 谢
