人教版数学八年级下册 18.1.2 平行四边形的判定(1)课件(共12张PPT)
文档属性
| 名称 | 人教版数学八年级下册 18.1.2 平行四边形的判定(1)课件(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 622.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 10:40:35 | ||
图片预览





文档简介
(共12张PPT)
第18章 平行四边形
18.1 平行四边形
18.1.2 平行四边形的判定(1)
一
学习目标
1.理解并掌握平行四边形的判定定理1、2、3.
2.能熟练运用平行四边形的判定定理进行证明.
二
重难点
重点:平行四边形判定定理的运用.
难点:平行四边形判定定理的证明.
1.知识回顾
三
教学过程
什么是平行四边形?平行四边形都有什么性质?
解:两组对边分别平行的四边形叫做平行四边形.平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.
2.情境导入
写出以上这些平行四边形的性质的逆命题?
解:(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
思考:这些命题都是真命题吗?
3.探究新知
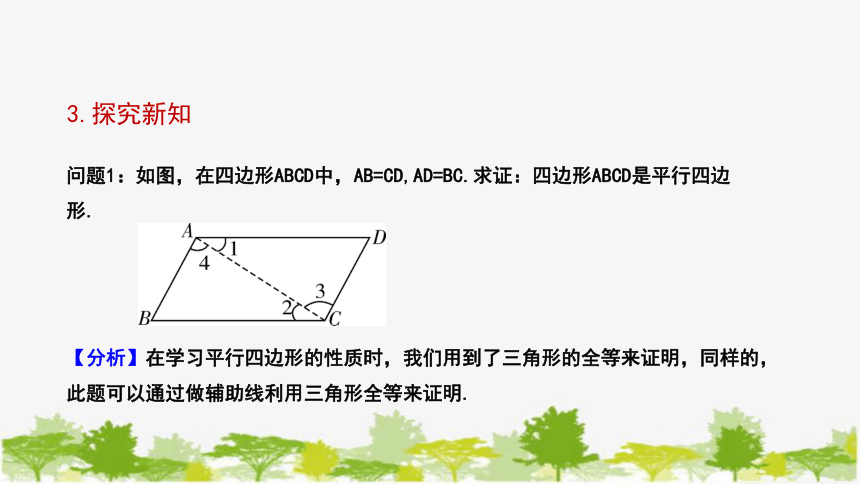
问题1:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.
【分析】在学习平行四边形的性质时,我们用到了三角形的全等来证明,同样的,此题可以通过做辅助线利用三角形全等来证明.
证明:连接AC,在△ABC和△CDA中,
AB=CD,AC=CA,BC=DA,
∴△ABC≌△CDA.
∴∠2=∠1,∠4=∠3.
∴AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形.
【知识归纳】两组对边分别相等的四边形是平行四边形.
这样就证明了两组对边分别相等的四边形是平行四边形为真命题.
问题2:已知:四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边形ABCD是平行四边形.
证明:∵∠A+∠C+∠B+∠D=360°,
又∵∠A=∠C,∠B=∠D,
∴2∠A+2∠B=360°,
即∠A+∠B=180°,
∴AD∥BC.同理得AB∥CD.
∴四边形ABCD是平行四边形.
这样就证明了两组对角分别相等的四边形是平行四边形为真命题.
【知识归纳】两组对角分别相等的四边形是平行四边形.
问题3:如图,在四边形ABCD中,AC,BD相交于点O,且OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
证明:∵OA=OC,OD=OB,∠AOD=∠COB,
∴△AOD≌△COB.
∴∠OAD=∠OCB.
∴AD∥BC.同理AB∥DC.
∴四边形ABCD是平行四边形.
这样就证明了对角线互相平分的四边形是平行四边形为真命题.
【知识归纳】对角线互相平分的四边形是平行四边形.
【分析】可以通过三角形全等来证明.
4.例题精讲
例1 如图, ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
∵AE=CF,
∴AO-AE=CO-CF,即EO=FO.
又BO=DO,
∴四边形BFDE是平行四边形.
例2 如图,在四边形ABCD中,AB∥DC,∠B=60°,∠1=80°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
解:(1)∵∠D+∠2+∠1=180°,∴∠D=180°-∠2-∠1=180°-40°-80°=60°;
(2)证明:∵AB∥DC,∴∠2=∠CAB.
∴∠DAB=∠1+∠CAB=∠1+∠2=120°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=360°-(∠DAB+∠D+∠B)=120°.
∴∠DCB=∠DAB.
又∠D=∠B=60°,
∴四边形ABCD是平行四边形.
6.课堂小结
1.平行四边形的判定定理;
2.平行四边形的性质和判定定理的综合应用.
第18章 平行四边形
18.1 平行四边形
18.1.2 平行四边形的判定(1)
一
学习目标
1.理解并掌握平行四边形的判定定理1、2、3.
2.能熟练运用平行四边形的判定定理进行证明.
二
重难点
重点:平行四边形判定定理的运用.
难点:平行四边形判定定理的证明.
1.知识回顾
三
教学过程
什么是平行四边形?平行四边形都有什么性质?
解:两组对边分别平行的四边形叫做平行四边形.平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.
2.情境导入
写出以上这些平行四边形的性质的逆命题?
解:(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
思考:这些命题都是真命题吗?
3.探究新知
问题1:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.
【分析】在学习平行四边形的性质时,我们用到了三角形的全等来证明,同样的,此题可以通过做辅助线利用三角形全等来证明.
证明:连接AC,在△ABC和△CDA中,
AB=CD,AC=CA,BC=DA,
∴△ABC≌△CDA.
∴∠2=∠1,∠4=∠3.
∴AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形.
【知识归纳】两组对边分别相等的四边形是平行四边形.
这样就证明了两组对边分别相等的四边形是平行四边形为真命题.
问题2:已知:四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边形ABCD是平行四边形.
证明:∵∠A+∠C+∠B+∠D=360°,
又∵∠A=∠C,∠B=∠D,
∴2∠A+2∠B=360°,
即∠A+∠B=180°,
∴AD∥BC.同理得AB∥CD.
∴四边形ABCD是平行四边形.
这样就证明了两组对角分别相等的四边形是平行四边形为真命题.
【知识归纳】两组对角分别相等的四边形是平行四边形.
问题3:如图,在四边形ABCD中,AC,BD相交于点O,且OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
证明:∵OA=OC,OD=OB,∠AOD=∠COB,
∴△AOD≌△COB.
∴∠OAD=∠OCB.
∴AD∥BC.同理AB∥DC.
∴四边形ABCD是平行四边形.
这样就证明了对角线互相平分的四边形是平行四边形为真命题.
【知识归纳】对角线互相平分的四边形是平行四边形.
【分析】可以通过三角形全等来证明.
4.例题精讲
例1 如图, ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
∵AE=CF,
∴AO-AE=CO-CF,即EO=FO.
又BO=DO,
∴四边形BFDE是平行四边形.
例2 如图,在四边形ABCD中,AB∥DC,∠B=60°,∠1=80°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
解:(1)∵∠D+∠2+∠1=180°,∴∠D=180°-∠2-∠1=180°-40°-80°=60°;
(2)证明:∵AB∥DC,∴∠2=∠CAB.
∴∠DAB=∠1+∠CAB=∠1+∠2=120°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=360°-(∠DAB+∠D+∠B)=120°.
∴∠DCB=∠DAB.
又∠D=∠B=60°,
∴四边形ABCD是平行四边形.
6.课堂小结
1.平行四边形的判定定理;
2.平行四边形的性质和判定定理的综合应用.
