2014年秋高中物理必修一(新人教版):第二章匀变速直线运动的研究 综合复习课件
文档属性
| 名称 | 2014年秋高中物理必修一(新人教版):第二章匀变速直线运动的研究 综合复习课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2014-09-17 00:00:00 | ||
图片预览








文档简介
课件25张PPT。本章综合复习?重点
1.匀变速直线运动的规律实验探究。
2.匀变速直线运动的规律及应用。
3.自由落体运动的规律及应用。
4.运动图象的理解和应用。
难点
1.匀变速直线运动的规律的理解。
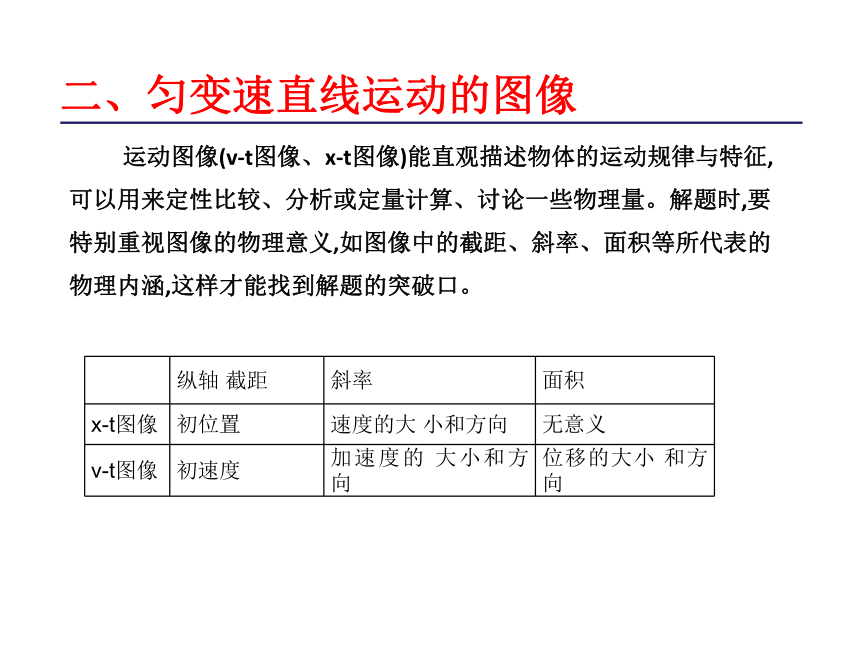
2.综合应用匀变速直线运动的规律解决问题的能力。重点难点一、匀变速直线运动问题的求解方法?典型例题例1火车刹车后7 s停下来,设火车做匀减速直线运动,最后1 s内的位移是2 m,求刹车过程中的位移是多少???二、匀变速直线运动的图像 运动图像(v-t图像、x-t图像)能直观描述物体的运动规律与特征,可以用来定性比较、分析或定量计算、讨论一些物理量。解题时,要特别重视图像的物理意义,如图像中的截距、斜率、面积等所代表的物理内涵,这样才能找到解题的突破口。1.自由落体运动三、自由落体运动与竖直上抛运动??典型例题???典型例题??四、追及与相遇问题(1)“速度相等”是两物体间距离最大或最小,恰好追上或恰好追不上,不相遇、相遇一次或相遇两次的临界条件。
(2)位移关系:若两物体从同一地点出发,经过一段时间后相遇,则两物体的位移相等;若两物体从不同地点出发,经过一段时间后相遇,则两物体的位移差为出发时两物体间的距离。
(3)仔细审题,注意抓住题目中的关键字眼,充分挖掘题目中的隐含条件,如“刚好”“恰好”“最多”“至少”等往往对应一个临界状态,要满足相应的临界条件。典型例题?典型例题?解析:有的同学认为两车是否相撞取决于刹车后两车位移之差是否大于250 m,甲车刹车后的位移x甲=v0甲22a甲=4022×1 m=800 m,乙车刹车后的位移x乙=v0乙22a乙=2022×13 m=600 m,因为x甲-x乙=200 m<250 m,所以两车不会相撞。其实,这种解法是错误的,只要作出它们的速度-时间图像,就一目了然了。如图所示,在t≤30 s时,v甲>v乙,两车距离减小,可能相撞;当t>30 s时,v甲 设两车速度相等所需时间为t0,则v0甲-a甲t0=v0乙-a乙t0,解得t0=30 s。此时两车的位移差Δx=v0甲t0-12a甲t02-v0乙 t0-12a乙t02=300 m>250 m,所以两车会相撞。
答案:两车会相撞。五、分析纸带的常用方法?3.求加速度
(1)逐差法
由于物体做匀变速直线运动,所以满足在连续相等的时间间隔内位移差相等,即Δx=aT2可得a=ΔxT2。但利用一个Δx求得的加速度偶然误差太大,为了减小实验中的偶然误差,分析纸带时,纸带上的各段位移最好都用上,方法如。
如果纸带上测得连续6个相同时间T内的位移x1、x2、x3、x4、x5、x6,如图所示,则
x4-x1=x4-x3+x3-x2+x2-x1=3a1T2
x5-x2=x5-x4+x4-x3+x3-x2=3a2T2
x6-x3=x6-x5+x5-x4+x4-x3=3a3T2
物体的加速度a=a1+a2+a33
=x4-x1+x5-x2+x6-x39T2
=x6+x5+x4-x3+x2+x19T2
由此可以看出,各段位移都用上了,有效地减小了偶然误差,这种方法被称为逐差法。所以利用纸带计算加速度时,应使用逐差法。(2)v-t图像法
利用上述2的方法,求出纸带上各点的瞬时速度v1、v2、v3、v4、v5,建立平面直角坐标系,以v为纵轴,t为横轴,描点、画直线,利用直线的斜率大小求加速度。?典型例题?例7 某同学在做“探究小车运动的速度与时间关系”的实验中:
(1)实验室提供了下列的实验器材:
①电火花计时器 ②天平 ③铁架台 ④秒表 ⑤刻度尺 ⑥细绳和纸带 ⑦一端有滑轮的长木板 ⑧钩码和小车
其中不需要的器材有: 。
(2)把实验过程中缺少的步骤填入空格。
①把一端附有滑轮的长木板平放在实验桌上,并使滑轮伸出桌面,把电火花计时器固定在长木板上远离滑轮的一端,连接好电路。
②纸带穿过限位孔,连接在小车的后面,用一条细绳拴在小车上,使细绳跨过滑轮,下边挂上合适的钩码, , ,让小车拖着纸带运动,打完一条后立即关闭电源。
③换上新纸带,重复操作两次。典型例题(3)选择一条合适的纸带,如图2-7所示,根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F五个点时小车的瞬时速度,请将vC、vE的速度值填入下表。(要求结果保留三位有效数字,各计数点间还有四个点未画出)(5)根据第(4)问中画出的v-t图线,求出的小车运动的加速度为 m/s2。(结果保留两位有效数字) (4)将B、C、D、E、F各个时刻的瞬时速度标在如图所示的坐标纸上,并画出小车的瞬时速度随时间变化的关系图线。?(4)v-t图像如图所示。
(5)根据图像的物理意义可知,在速度—时间图像中,图像的斜率大小表示物体的加速度大小,故a=ΔvΔt=0.80 m/s2。
答案:(1)②④ (2)启动电源 放开小车 (3)0.479 0.640 (4)如图2-9所示。 (5)0.80
1.匀变速直线运动的规律实验探究。
2.匀变速直线运动的规律及应用。
3.自由落体运动的规律及应用。
4.运动图象的理解和应用。
难点
1.匀变速直线运动的规律的理解。
2.综合应用匀变速直线运动的规律解决问题的能力。重点难点一、匀变速直线运动问题的求解方法?典型例题例1火车刹车后7 s停下来,设火车做匀减速直线运动,最后1 s内的位移是2 m,求刹车过程中的位移是多少???二、匀变速直线运动的图像 运动图像(v-t图像、x-t图像)能直观描述物体的运动规律与特征,可以用来定性比较、分析或定量计算、讨论一些物理量。解题时,要特别重视图像的物理意义,如图像中的截距、斜率、面积等所代表的物理内涵,这样才能找到解题的突破口。1.自由落体运动三、自由落体运动与竖直上抛运动??典型例题???典型例题??四、追及与相遇问题(1)“速度相等”是两物体间距离最大或最小,恰好追上或恰好追不上,不相遇、相遇一次或相遇两次的临界条件。
(2)位移关系:若两物体从同一地点出发,经过一段时间后相遇,则两物体的位移相等;若两物体从不同地点出发,经过一段时间后相遇,则两物体的位移差为出发时两物体间的距离。
(3)仔细审题,注意抓住题目中的关键字眼,充分挖掘题目中的隐含条件,如“刚好”“恰好”“最多”“至少”等往往对应一个临界状态,要满足相应的临界条件。典型例题?典型例题?解析:有的同学认为两车是否相撞取决于刹车后两车位移之差是否大于250 m,甲车刹车后的位移x甲=v0甲22a甲=4022×1 m=800 m,乙车刹车后的位移x乙=v0乙22a乙=2022×13 m=600 m,因为x甲-x乙=200 m<250 m,所以两车不会相撞。其实,这种解法是错误的,只要作出它们的速度-时间图像,就一目了然了。如图所示,在t≤30 s时,v甲>v乙,两车距离减小,可能相撞;当t>30 s时,v甲
答案:两车会相撞。五、分析纸带的常用方法?3.求加速度
(1)逐差法
由于物体做匀变速直线运动,所以满足在连续相等的时间间隔内位移差相等,即Δx=aT2可得a=ΔxT2。但利用一个Δx求得的加速度偶然误差太大,为了减小实验中的偶然误差,分析纸带时,纸带上的各段位移最好都用上,方法如。
如果纸带上测得连续6个相同时间T内的位移x1、x2、x3、x4、x5、x6,如图所示,则
x4-x1=x4-x3+x3-x2+x2-x1=3a1T2
x5-x2=x5-x4+x4-x3+x3-x2=3a2T2
x6-x3=x6-x5+x5-x4+x4-x3=3a3T2
物体的加速度a=a1+a2+a33
=x4-x1+x5-x2+x6-x39T2
=x6+x5+x4-x3+x2+x19T2
由此可以看出,各段位移都用上了,有效地减小了偶然误差,这种方法被称为逐差法。所以利用纸带计算加速度时,应使用逐差法。(2)v-t图像法
利用上述2的方法,求出纸带上各点的瞬时速度v1、v2、v3、v4、v5,建立平面直角坐标系,以v为纵轴,t为横轴,描点、画直线,利用直线的斜率大小求加速度。?典型例题?例7 某同学在做“探究小车运动的速度与时间关系”的实验中:
(1)实验室提供了下列的实验器材:
①电火花计时器 ②天平 ③铁架台 ④秒表 ⑤刻度尺 ⑥细绳和纸带 ⑦一端有滑轮的长木板 ⑧钩码和小车
其中不需要的器材有: 。
(2)把实验过程中缺少的步骤填入空格。
①把一端附有滑轮的长木板平放在实验桌上,并使滑轮伸出桌面,把电火花计时器固定在长木板上远离滑轮的一端,连接好电路。
②纸带穿过限位孔,连接在小车的后面,用一条细绳拴在小车上,使细绳跨过滑轮,下边挂上合适的钩码, , ,让小车拖着纸带运动,打完一条后立即关闭电源。
③换上新纸带,重复操作两次。典型例题(3)选择一条合适的纸带,如图2-7所示,根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F五个点时小车的瞬时速度,请将vC、vE的速度值填入下表。(要求结果保留三位有效数字,各计数点间还有四个点未画出)(5)根据第(4)问中画出的v-t图线,求出的小车运动的加速度为 m/s2。(结果保留两位有效数字) (4)将B、C、D、E、F各个时刻的瞬时速度标在如图所示的坐标纸上,并画出小车的瞬时速度随时间变化的关系图线。?(4)v-t图像如图所示。
(5)根据图像的物理意义可知,在速度—时间图像中,图像的斜率大小表示物体的加速度大小,故a=ΔvΔt=0.80 m/s2。
答案:(1)②④ (2)启动电源 放开小车 (3)0.479 0.640 (4)如图2-9所示。 (5)0.80
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
