用多边形拼地板[下学期]
图片预览






文档简介
课件23张PPT。用正多边形拼地板1.导入新课
2.新课讲述
3.例题讲述
4.课堂练习
5.课堂小结
6.课外作业复习1 什么是正多边形?如果多边形的各边都相等,各内角也都相等,那么
就称它为正多边形。
2 多边形的内角和公式是什么?外角和?多边形的内角和公式: (n-2)×180
多边形的外角和为360度
观察与思考观察与思考观察与思考观察与思考观察与思考问:每个内角为多少度的时候能拼成一个
既不留下一丝空白,又不相互重叠的平面
图形?答:周角360°是正多边形的一个内角度
数的整数倍时,用这样的正多边形能铺
满平面。 例如:正三角形,正方形等。例题讲述例1:正九边形能不能铺满平面?为什么讨论:一个正多边形能不能铺满平面,只要看周角360度能不能被一个内角度数整除,如果能整除,则能铺满平面;如果不能整除,则不能铺满平面。解:因为正九边形每个内角为140度,又
因为周角360不能被140整除,所以正九
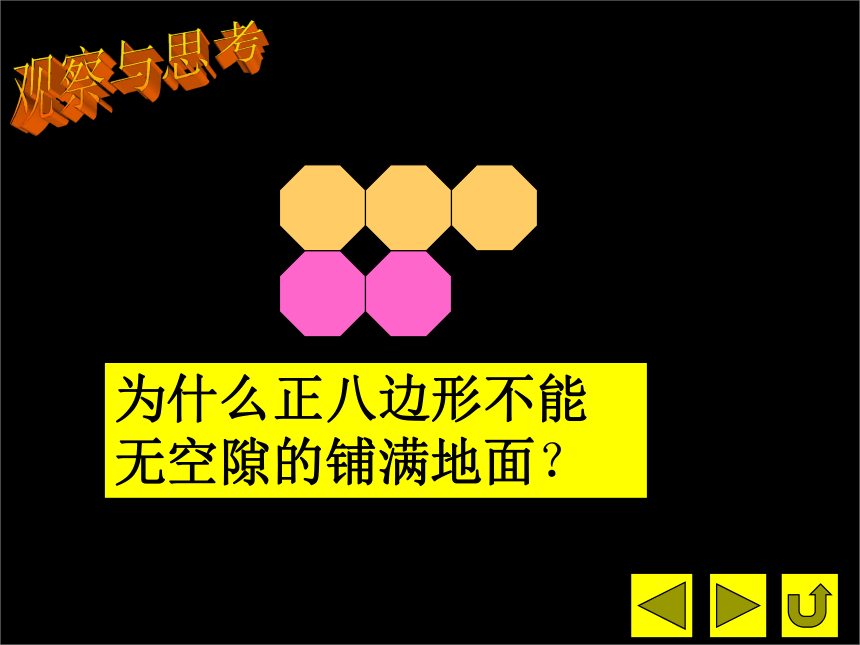
边形不能铺满平面。观察与思考为什么正八边形不能
无空隙的铺满地面?课堂练习那么正三角形和正六边形呢?把正三角形、正方形、正六边形三者结合在一起呢?请你试试看。
虑考:正三角形和正六边形的内角分别是
多少?怎样组合就能得到的周角是
360度?用两种正多边形镶嵌,哪些能镶嵌成一个平面?2m+3n=12m=3
n=2设在一个顶点周围有m个正三角形的角、n个正方形的角,
则有
∵m、n为正整数∴解为如图:把相邻两行正三角形分开,添一行正方形,
得到下面的图。他表明把正三角形和正方形结合在
一起也能铺满地面。为什么?例题讲述因为:正三角形的内角为60度,正方形的内角为90度,这样用3块正三角形和2块正方形,他们的内角和为一个周角360度,所以能铺满地面。课堂练习结论:几种正多边形的组合,各取其中几个内角相加恰为一个周角360度时,这样的正多边形的组合能铺满平面。
1. 能够铺满平面的正多边形组合是( )A. 正八边形和正方形B. 正五边形和正十边形C. 正六边形和正三角形答案:AC课堂练习课堂小结周角360度是正多边形的一个内角度数的整
数倍时,用这样的正多边形能铺满平面!例如:用六个正三角形能铺满地面就是:
6×60° =360°
用四个正方形能铺满地面就是:
4×90 °=360°课堂小结几种正多边形的组合,各取其中几个内角
相加恰为一个周角360度时,这样的正多
边形的组合能铺满平面。例如:正三角形和正方形。正三角形的内角为
60度,正方形的内角为90度,这样用3块
正三角形和2块正方形,他们的内角和为
一个周角360度,所以能铺满地面。
2.新课讲述
3.例题讲述
4.课堂练习
5.课堂小结
6.课外作业复习1 什么是正多边形?如果多边形的各边都相等,各内角也都相等,那么
就称它为正多边形。
2 多边形的内角和公式是什么?外角和?多边形的内角和公式: (n-2)×180
多边形的外角和为360度
观察与思考观察与思考观察与思考观察与思考观察与思考问:每个内角为多少度的时候能拼成一个
既不留下一丝空白,又不相互重叠的平面
图形?答:周角360°是正多边形的一个内角度
数的整数倍时,用这样的正多边形能铺
满平面。 例如:正三角形,正方形等。例题讲述例1:正九边形能不能铺满平面?为什么讨论:一个正多边形能不能铺满平面,只要看周角360度能不能被一个内角度数整除,如果能整除,则能铺满平面;如果不能整除,则不能铺满平面。解:因为正九边形每个内角为140度,又
因为周角360不能被140整除,所以正九
边形不能铺满平面。观察与思考为什么正八边形不能
无空隙的铺满地面?课堂练习那么正三角形和正六边形呢?把正三角形、正方形、正六边形三者结合在一起呢?请你试试看。
虑考:正三角形和正六边形的内角分别是
多少?怎样组合就能得到的周角是
360度?用两种正多边形镶嵌,哪些能镶嵌成一个平面?2m+3n=12m=3
n=2设在一个顶点周围有m个正三角形的角、n个正方形的角,
则有
∵m、n为正整数∴解为如图:把相邻两行正三角形分开,添一行正方形,
得到下面的图。他表明把正三角形和正方形结合在
一起也能铺满地面。为什么?例题讲述因为:正三角形的内角为60度,正方形的内角为90度,这样用3块正三角形和2块正方形,他们的内角和为一个周角360度,所以能铺满地面。课堂练习结论:几种正多边形的组合,各取其中几个内角相加恰为一个周角360度时,这样的正多边形的组合能铺满平面。
1. 能够铺满平面的正多边形组合是( )A. 正八边形和正方形B. 正五边形和正十边形C. 正六边形和正三角形答案:AC课堂练习课堂小结周角360度是正多边形的一个内角度数的整
数倍时,用这样的正多边形能铺满平面!例如:用六个正三角形能铺满地面就是:
6×60° =360°
用四个正方形能铺满地面就是:
4×90 °=360°课堂小结几种正多边形的组合,各取其中几个内角
相加恰为一个周角360度时,这样的正多
边形的组合能铺满平面。例如:正三角形和正方形。正三角形的内角为
60度,正方形的内角为90度,这样用3块
正三角形和2块正方形,他们的内角和为
一个周角360度,所以能铺满地面。
