19.1.2矩形[下学期]
文档属性
| 名称 | 19.1.2矩形[下学期] |
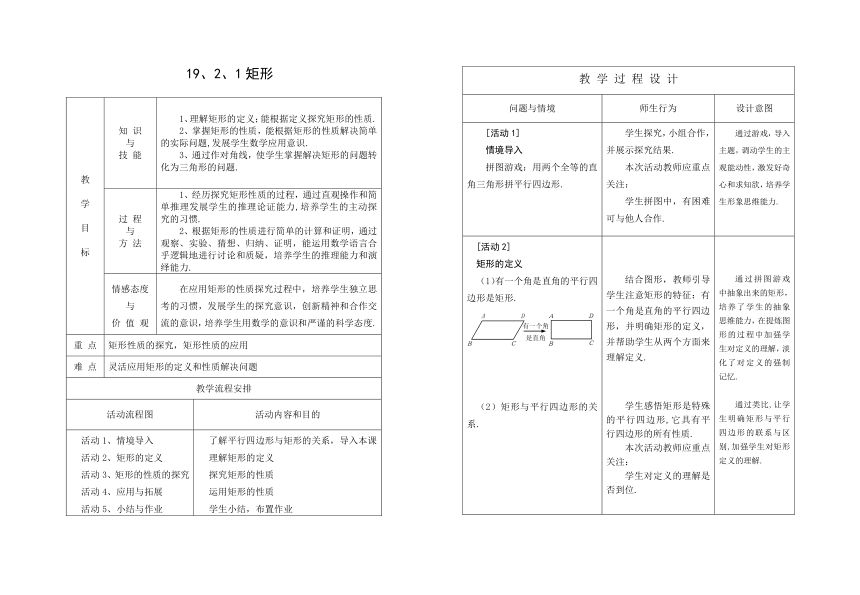
|
|
| 格式 | rar | ||
| 文件大小 | 12.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-19 00:00:00 | ||
图片预览

文档简介
19、2、1矩形
教学目标 知 识与技 能 1、理解矩形的定义;能根据定义探究矩形的性质.2、掌握矩形的性质,能根据矩形的性质解决简单的实际问题,发展学生数学应用意识.3、通过作对角线,使学生掌握解决矩形的问题转化为三角形的问题.
过 程与方 法 1、经历探究矩形性质的过程,通过直观操作和简单推理发展学生的推理论证能力,培养学生的主动探究的习惯.2、根据矩形的性质进行简单的计算和证明,通过观察、实验、猜想、归纳、证明,能运用数学语言合乎逻辑地进行讨论和质疑,培养学生的推理能力和演绎能力.
情感态度与价 值 观 在应用矩形的性质探究过程中,培养学生独立思考的习惯,发展学生的探究意识,创新精神和合作交流的意识,培养学生用数学的意识和严谨的科学态度.
重 点 矩形性质的探究,矩形性质的应用
难 点 灵活应用矩形的定义和性质解决问题
教学流程安排
活动流程图 活动内容和目的
活动1、情境导入活动2、矩形的定义活动3、矩形的性质的探究活动4、应用与拓展活动5、小结与作业 了解平行四边形与矩形的关系,导入本课理解矩形的定义探究矩形的性质运用矩形的性质学生小结,布置作业
教 学 过 程 设 计
问题与情境 师生行为 设计意图
[活动1]情境导入拼图游戏:用两个全等的直角三角形拼平行四边形. 学生探究,小组合作,并展示探究结果.本次活动教师应重点关注:学生拼图中,有困难可与他人合作. 通过游戏,导入主题,调动学生的主观能动性,激发好奇心和求知欲,培养学生形象思维能力.
[活动2]矩形的定义(1)有一个角是直角的平行四边形是矩形.A D A D(2)矩形与平行四边形的关系. 结合图形,教师引导学生注意矩形的特征:有一个角是直角的平行四边形,并明确矩形的定义,并帮助学生从两个方面来理解定义.学生感悟矩形是特殊的平行四边形,它具有平行四边形的所有性质.本次活动教师应重点关注:学生对定义的理解是否到位. 通过拼图游戏中抽象出来的矩形,培养了学生的抽象思维能力,在提炼图形的过程中加强学生对定义的理解,淡化了对定义的强制记忆.通过类比,让学生明确矩形与平行四边形的联系与区别,加强学生对矩形定义的理解.
问题与情境 师生行为 设计意图
[活动3]矩形性质的探究(1)矩形除了具有平行四边形的所有性质外,它还有什么特殊的性质?(2)你能证明你发现的结论吗?(3)矩形能转化成哪些直角三角形,等腰三角形?(4)议一议:矩形ABCD中,对角线AC、BD相交于点D,请探究对OC与BD 的数量关系. 教师提出问题(1)后,学生通过学具演示,引导学生观察、度量、猜想,学生利用学具演示、观察、度量、猜想出矩形的四个角都是直角,对角线相等等性质.教师提出问题(2)后,学生独立思考,再自主交流.教师提出问题(3)后,学生思考后回答.教师提出问题(4)学生独立思考后,通过交流得到直角三角形的一个性质:直角三角形斜边上的中线等于斜边的一半. 通过学具演示,学生加强了对矩形的定义的感性认识,感受演示、观察、度量、猜想的乐趣,培养猜想的意识.学生独立完成证明,培养了学生的推理能力,通过证明,验证了猜想的正确,让学生感受数学结论的确定性和证明的必要性.让学生体会转化的数学思想.
问题与情境 师生行为 设计意图
(5)矩形是轴对称图形吗?它有几条对称轴?(6)矩形性质的小结 学生对矩形纸片折叠,得出结论.本次活动教师要重点关注:(1)学生的探究过程应循序渐进,即演示 观察 度量 猜想 证明.(2)要给学生充足的时间和空间. 通过用几何语言对性质的表述,是学生对矩形特征的再认识,是知识的一次升华,培养学生的概括能力,突出教学重点.
[活动4]应用与拓展1、学生解决P104例1.2、小试牛刀(1)如果矩形ABCD的一条对角线AC长为8cm,BOC=120,则AB= cm. 教师引导学生审题,学生独立完成后,小组交流,并把不同的结果展示出来. 通过例题学生进一步理解应用矩形的性质,强化学生规范答题的能力.
问题与情境 师生行为 设计意图
(2)如图,矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果BAF=60,则EAF等于( )A、15 B、30C、45 D、603、思考题:(根据2005年梅州市中考题改编)如图,已知四边形ABCD是矩形,O是对角线AC、BD的交点,点E在对角线AC上,点F在对角线BD上.(1)如果 ,则DOE≌AOF(请你填一个使结论成立的条件). (2)试证明你的结论. 本次活动教师应重点关注:(1)矩形的性质在应用时的几何语言表述.(2)点评针对性、典型性.(3)鼓励学生一题多解.(4)给学生相对充足的探究时间和空间. 让学生运用矩形的性质, 学会解决简单的实际问题,让学生认识到现实生活中蕴含着大量的数学信息,培养学生的应用意识.
问题与情境 师生行为 设计意图
[活动5]小结作业(1)本节课你有什么收获?(2)作业布置必做题①P112,T3②如图,已知BD、CE是ABC的两条高,M是BC的中点,求证:EM=DM选做题:矩形的性质1、2的逆命题是什么?它们是真命题吗? 学生交流获得的知识和感受;教师聆听,并与学生交流.本次活动中教师应关注:(1)学生概括的性质是否全面,应及时补充.(2)不同层次的学生,对知识的掌握的程度. 通过小结,概括出本节课的知识与方法,体验探究过程中的感受.
有一个角
是直角
B
C
C
B
B
C
O
A
D
A
D
E
B
F
C
C
D
F
E
O
A
B
A
C
M
B
D
E
教学目标 知 识与技 能 1、理解矩形的定义;能根据定义探究矩形的性质.2、掌握矩形的性质,能根据矩形的性质解决简单的实际问题,发展学生数学应用意识.3、通过作对角线,使学生掌握解决矩形的问题转化为三角形的问题.
过 程与方 法 1、经历探究矩形性质的过程,通过直观操作和简单推理发展学生的推理论证能力,培养学生的主动探究的习惯.2、根据矩形的性质进行简单的计算和证明,通过观察、实验、猜想、归纳、证明,能运用数学语言合乎逻辑地进行讨论和质疑,培养学生的推理能力和演绎能力.
情感态度与价 值 观 在应用矩形的性质探究过程中,培养学生独立思考的习惯,发展学生的探究意识,创新精神和合作交流的意识,培养学生用数学的意识和严谨的科学态度.
重 点 矩形性质的探究,矩形性质的应用
难 点 灵活应用矩形的定义和性质解决问题
教学流程安排
活动流程图 活动内容和目的
活动1、情境导入活动2、矩形的定义活动3、矩形的性质的探究活动4、应用与拓展活动5、小结与作业 了解平行四边形与矩形的关系,导入本课理解矩形的定义探究矩形的性质运用矩形的性质学生小结,布置作业
教 学 过 程 设 计
问题与情境 师生行为 设计意图
[活动1]情境导入拼图游戏:用两个全等的直角三角形拼平行四边形. 学生探究,小组合作,并展示探究结果.本次活动教师应重点关注:学生拼图中,有困难可与他人合作. 通过游戏,导入主题,调动学生的主观能动性,激发好奇心和求知欲,培养学生形象思维能力.
[活动2]矩形的定义(1)有一个角是直角的平行四边形是矩形.A D A D(2)矩形与平行四边形的关系. 结合图形,教师引导学生注意矩形的特征:有一个角是直角的平行四边形,并明确矩形的定义,并帮助学生从两个方面来理解定义.学生感悟矩形是特殊的平行四边形,它具有平行四边形的所有性质.本次活动教师应重点关注:学生对定义的理解是否到位. 通过拼图游戏中抽象出来的矩形,培养了学生的抽象思维能力,在提炼图形的过程中加强学生对定义的理解,淡化了对定义的强制记忆.通过类比,让学生明确矩形与平行四边形的联系与区别,加强学生对矩形定义的理解.
问题与情境 师生行为 设计意图
[活动3]矩形性质的探究(1)矩形除了具有平行四边形的所有性质外,它还有什么特殊的性质?(2)你能证明你发现的结论吗?(3)矩形能转化成哪些直角三角形,等腰三角形?(4)议一议:矩形ABCD中,对角线AC、BD相交于点D,请探究对OC与BD 的数量关系. 教师提出问题(1)后,学生通过学具演示,引导学生观察、度量、猜想,学生利用学具演示、观察、度量、猜想出矩形的四个角都是直角,对角线相等等性质.教师提出问题(2)后,学生独立思考,再自主交流.教师提出问题(3)后,学生思考后回答.教师提出问题(4)学生独立思考后,通过交流得到直角三角形的一个性质:直角三角形斜边上的中线等于斜边的一半. 通过学具演示,学生加强了对矩形的定义的感性认识,感受演示、观察、度量、猜想的乐趣,培养猜想的意识.学生独立完成证明,培养了学生的推理能力,通过证明,验证了猜想的正确,让学生感受数学结论的确定性和证明的必要性.让学生体会转化的数学思想.
问题与情境 师生行为 设计意图
(5)矩形是轴对称图形吗?它有几条对称轴?(6)矩形性质的小结 学生对矩形纸片折叠,得出结论.本次活动教师要重点关注:(1)学生的探究过程应循序渐进,即演示 观察 度量 猜想 证明.(2)要给学生充足的时间和空间. 通过用几何语言对性质的表述,是学生对矩形特征的再认识,是知识的一次升华,培养学生的概括能力,突出教学重点.
[活动4]应用与拓展1、学生解决P104例1.2、小试牛刀(1)如果矩形ABCD的一条对角线AC长为8cm,BOC=120,则AB= cm. 教师引导学生审题,学生独立完成后,小组交流,并把不同的结果展示出来. 通过例题学生进一步理解应用矩形的性质,强化学生规范答题的能力.
问题与情境 师生行为 设计意图
(2)如图,矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果BAF=60,则EAF等于( )A、15 B、30C、45 D、603、思考题:(根据2005年梅州市中考题改编)如图,已知四边形ABCD是矩形,O是对角线AC、BD的交点,点E在对角线AC上,点F在对角线BD上.(1)如果 ,则DOE≌AOF(请你填一个使结论成立的条件). (2)试证明你的结论. 本次活动教师应重点关注:(1)矩形的性质在应用时的几何语言表述.(2)点评针对性、典型性.(3)鼓励学生一题多解.(4)给学生相对充足的探究时间和空间. 让学生运用矩形的性质, 学会解决简单的实际问题,让学生认识到现实生活中蕴含着大量的数学信息,培养学生的应用意识.
问题与情境 师生行为 设计意图
[活动5]小结作业(1)本节课你有什么收获?(2)作业布置必做题①P112,T3②如图,已知BD、CE是ABC的两条高,M是BC的中点,求证:EM=DM选做题:矩形的性质1、2的逆命题是什么?它们是真命题吗? 学生交流获得的知识和感受;教师聆听,并与学生交流.本次活动中教师应关注:(1)学生概括的性质是否全面,应及时补充.(2)不同层次的学生,对知识的掌握的程度. 通过小结,概括出本节课的知识与方法,体验探究过程中的感受.
有一个角
是直角
B
C
C
B
B
C
O
A
D
A
D
E
B
F
C
C
D
F
E
O
A
B
A
C
M
B
D
E
