图形的全等 复习课

课件17张PPT。小结与思考㈠制作：范大阳
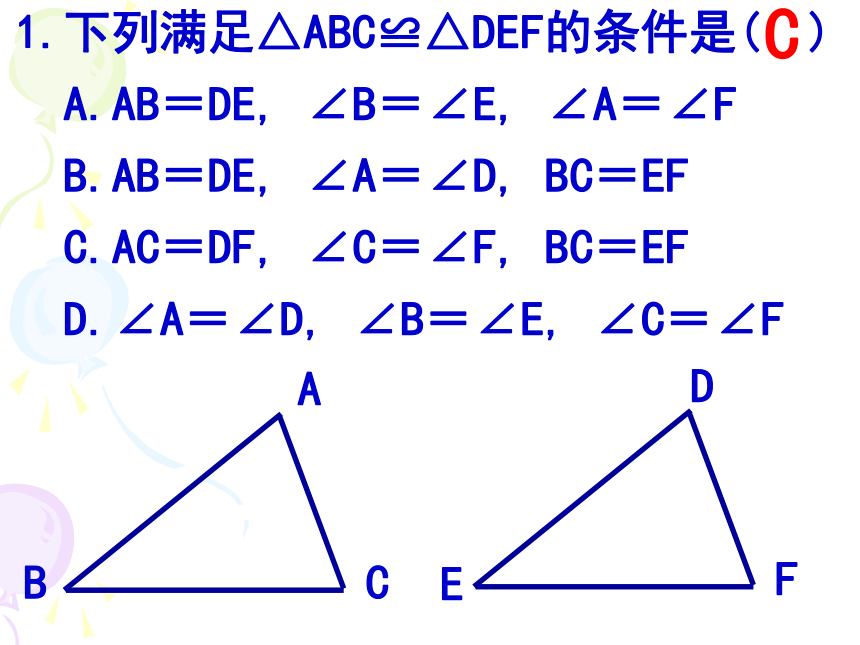
审核：韩宝华1.下列满足△ABC≌△DEF的条件是( )
A.AB＝DE, ∠B＝∠E, ∠A＝∠F
B.AB＝DE, ∠A＝∠D, BC＝EF
C.AC＝DF, ∠C＝∠F, BC＝EF
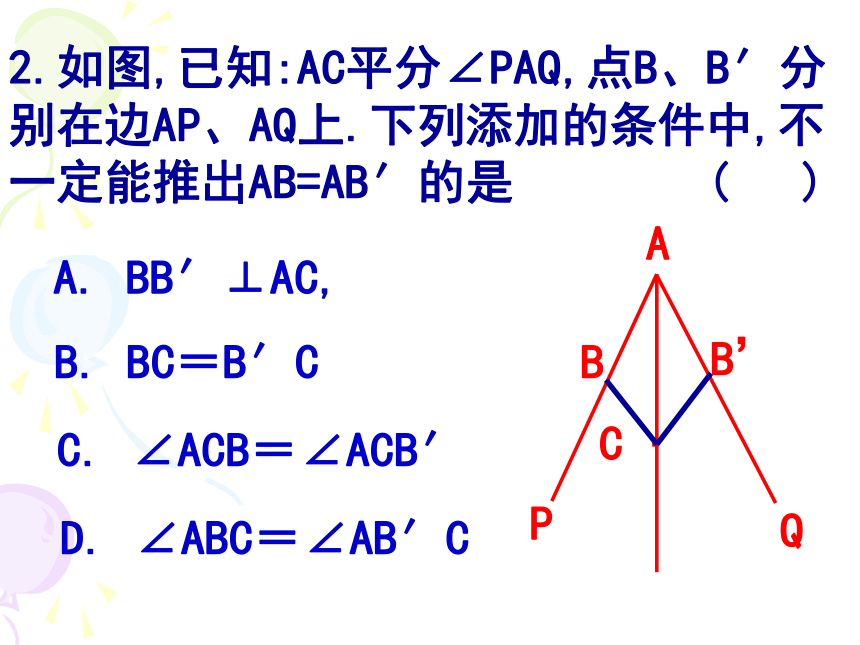
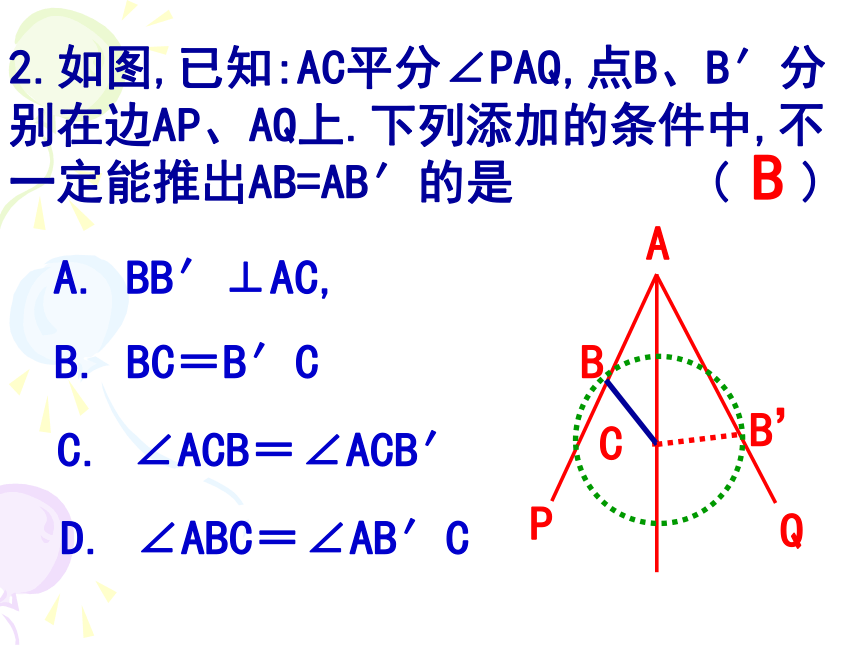
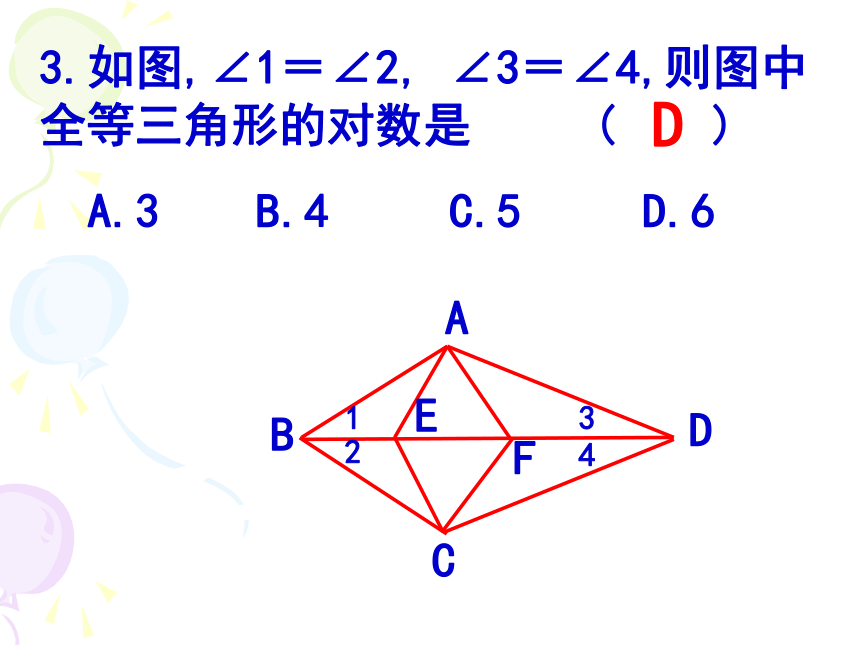
D.∠A＝∠D, ∠B＝∠E, ∠C＝∠FCABCDEF2.如图,已知:AC平分∠PAQ,点B、B′分别在边AP、AQ上.下列添加的条件中,不一定能推出AB=AB′的是　　　　( )A. BB′⊥AC,B. BC＝B′CC. ∠ACB＝∠ACB′D. ∠ABC＝∠AB′CAPQC ·2.如图,已知:AC平分∠PAQ,点B、B′分别在边AP、AQ上.下列添加的条件中,不一定能推出AB=AB′的是　　　　( )A. BB′⊥AC,B. BC＝B′CC. ∠ACB＝∠ACB′D. ∠ABC＝∠AB′CAPQC ·BB3.如图,∠1＝∠2, ∠3＝∠4,则图中全等三角形的对数是 ( )
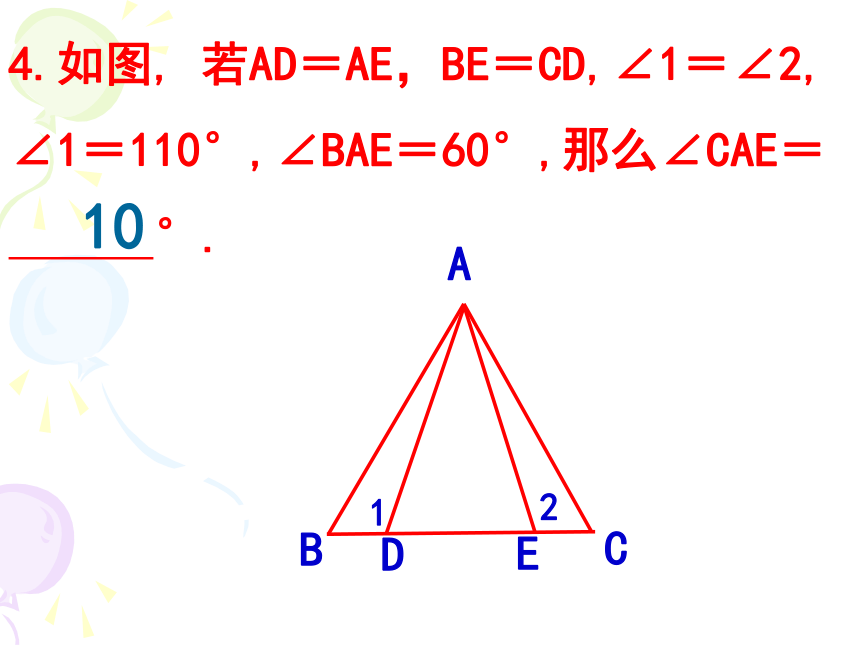
A.3 B.4 C.5 D.6D4.如图, 若AD＝AE，BE＝CD,∠1＝∠2,
∠1＝110°,∠BAE＝60°,那么∠CAE＝
°.
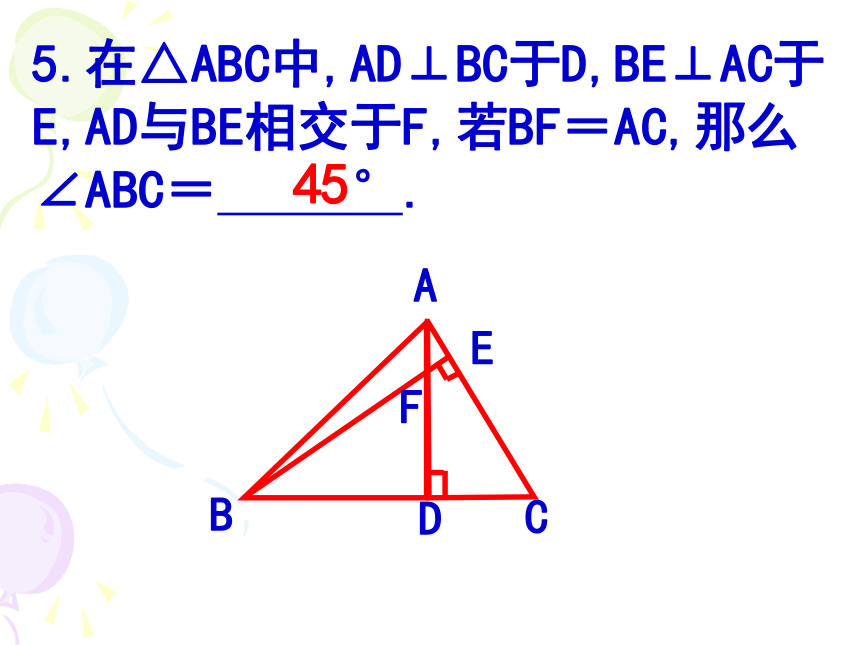
105.在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF＝AC,那么∠ABC＝ °.45操作思考与1.如图，将长方形ABCD沿直线BD折叠一次 (折痕与折叠后得到的图形用虚线表示),请将得到的所有全等三角形(包括实线、虚线在内）， 用符号表示出来.并说明理由.BCDAEF 2. 如图,△ABC中,∠BCA＝90°,AM⊥AC于A点,点P、Q分别在直线AC、AM上运动，（P点可以与C、A重合）当点P与点Q分别运动到什么位置时，才能使△ABC与△PQA全等？这样的△PQA有几个？M如图，在△ABE和△ACD中，给出以下四个论断:⑴ AB ＝ AC; ⑵ AD ＝ AE; ⑶ AD⊥DC, AE⊥BE; ⑷ AM ＝ AN .能否以其中三个论断为条件,另一个论断为结论,使之组成一个正确的推断?说明理由.运用思考与1.已知:如图,AB＝CD,AD＝BC,
AC、BD相交于点O.⑴你能发现哪些结论.试说明你的理由.⑵.请你在该图上过点O画直线EF分别交AB 、CD于点E、F;过点O画直线GH,分别交AD、BC于点G、H,试问图中共有多少对全等三角形?2.如图,点B、C、D在同一条直线上，△ABC、△ADE都是等边三角形.试猜想CE与AC＋DC的大小关系,并说明理由.3.如图,AD⊥AB,AE⊥AC,且AD＝AB,
AE＝AC.试说明BE与CD的关系.9.如图，已知：AC＝BC, CD⊥CE, DA⊥AB,BE⊥AB,垂足分别为C、A、B.试说明:DE＝AD＋BE.教学反思 ●通过本节课的学习,你有哪些收获? ●本节课你还有哪些疑问?预习指南因式分解复习