第7课时 间接证明1
图片预览








文档简介
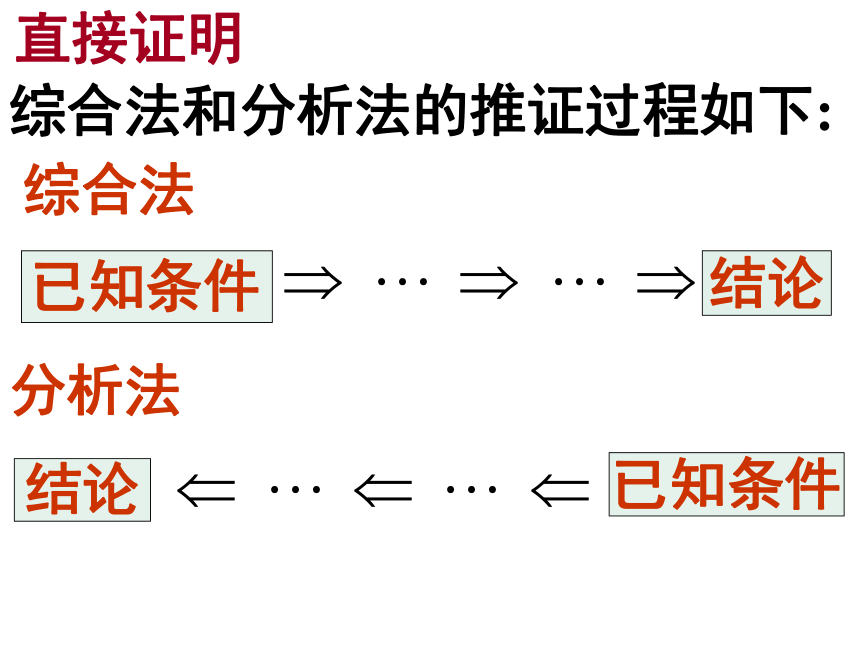
课件24张PPT。1直接证明概念2 直接证明的一般形式:直接从原命题的条件逐步推得命题成立一、知识回顾:直接证明方法有几种?都是直接证明综合法:从已知条件出发,以已知的定义、公理、定理为依据,逐步下推,直到推出要证明的结论为止相同不同 分析法:从问题的结论出发,追溯导致结论成立的条件,逐步上溯,直到使结论成立的条件和已知条件吻合为止证法有什么异同?有两种:综合法、分析法直接证明综合法和分析法的推证过程如下:综合法已知条件结论分析法结论 已知条件 第92课时 间接证明(1)问题情境上述证明不同于直接证明这种证明通常称为间接证明间接证明(基本概念)间接证明:不是直接从命题的条件逐步推得命题成立.间接证明的主要方法---反证法.反证法是一种常用的间接证明方法. 否定结论 导致矛盾 否定命题
不成立 原结论成立 合理的推理 思考? A、B、C三个人,A说B撒谎,B说C撒谎,C说A、B都撒谎.则C必定是在撒谎,为什么?分析:假设C没有撒谎, 则C真. - - -- -那么A假且B假;由A假, 知B真. 这与B假矛盾.那么假设C没有撒谎不成立;则C必定是在撒谎.间接证明(基本概念)反证法的过程包括以下三个步骤:(1)反设——假设命题的结论不成立,即假定原命题的反面为真;(2)归谬——从反设和已知条件出发,经过一系列正确的逻辑推理,得出矛盾结果;(3)存真——由矛盾结果,断定反设不真,从而肯定原结论成立.反证法的思维方法:正难则反应用反证法的情形:(1)直接证明困难;
(2)需分成很多类进行讨论.
(3)结论为“至少”、“至多”、“有无穷多个” 类命题;
(4)结论为 “唯一”类命题;间接证明(例题1)先求出周期 思路 用反证法证明2?是最小正周期.间接证明(例题1) 假设T是正弦函数的周期则对任意实数x都有:解:令x=0,得即从而对任意实数x都应有这与 矛盾.因此,原命题成立.间接证明(习题1)1.求证:若一个整数的平方是偶数,则这个数也是偶数.证:假设这个数是奇数,可以设为2k+1,则有而不是偶数这与原命题条件矛盾.2 求证: 是无理数.例3.已知函数f(x)是(-?,+?)上的增函数,a,b?R.
(1)证明命题:若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b).
(2)判断(1)的逆命题是否成立,并证明你的结论.间接证明(回顾小结)间接证明 反证法 同一法 枚举法 完全归纳法 例1:用反证法证明:
如果a>b>0,那么例2 已知a≠0,证明x的方程ax=b有且只有一个根。例3:证明:圆的两条不全是直径的相交弦不能互相平分.已知:在⊙O中,弦AB、CD相交于P,且AB、CD不全是直径 求证:AB、CD不能互相平分。ABCD练习间接证明3. 设函数,求证:中至少有一个不小于1.间接证明已知:求证:(2)中至少有一个不小于.(1)再见!同学们.再见!
不成立 原结论成立 合理的推理 思考? A、B、C三个人,A说B撒谎,B说C撒谎,C说A、B都撒谎.则C必定是在撒谎,为什么?分析:假设C没有撒谎, 则C真. - - -- -那么A假且B假;由A假, 知B真. 这与B假矛盾.那么假设C没有撒谎不成立;则C必定是在撒谎.间接证明(基本概念)反证法的过程包括以下三个步骤:(1)反设——假设命题的结论不成立,即假定原命题的反面为真;(2)归谬——从反设和已知条件出发,经过一系列正确的逻辑推理,得出矛盾结果;(3)存真——由矛盾结果,断定反设不真,从而肯定原结论成立.反证法的思维方法:正难则反应用反证法的情形:(1)直接证明困难;
(2)需分成很多类进行讨论.
(3)结论为“至少”、“至多”、“有无穷多个” 类命题;
(4)结论为 “唯一”类命题;间接证明(例题1)先求出周期 思路 用反证法证明2?是最小正周期.间接证明(例题1) 假设T是正弦函数的周期则对任意实数x都有:解:令x=0,得即从而对任意实数x都应有这与 矛盾.因此,原命题成立.间接证明(习题1)1.求证:若一个整数的平方是偶数,则这个数也是偶数.证:假设这个数是奇数,可以设为2k+1,则有而不是偶数这与原命题条件矛盾.2 求证: 是无理数.例3.已知函数f(x)是(-?,+?)上的增函数,a,b?R.
(1)证明命题:若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b).
(2)判断(1)的逆命题是否成立,并证明你的结论.间接证明(回顾小结)间接证明 反证法 同一法 枚举法 完全归纳法 例1:用反证法证明:
如果a>b>0,那么例2 已知a≠0,证明x的方程ax=b有且只有一个根。例3:证明:圆的两条不全是直径的相交弦不能互相平分.已知:在⊙O中,弦AB、CD相交于P,且AB、CD不全是直径 求证:AB、CD不能互相平分。ABCD练习间接证明3. 设函数,求证:中至少有一个不小于1.间接证明已知:求证:(2)中至少有一个不小于.(1)再见!同学们.再见!
